基于改进粒子群算法的精准农业无线传感器定位研究
2019-03-21刘勇军
程 磊,刘勇军
(黄淮学院智能制造学院,河南 驻马店 463000)
0 引 言
精细农业以最少的投入获得优质的高产出和高效益,借助无线传感器网络,能实时远程获取农田土壤、植物生态等信息,精确地进行作业,有效节约资源[1,2]。
精准农业无线传感器定位算法主要分为两类[3]:一类为基于测距的定位算法,利用信标节点的位置信息实现未知节点的位置估计,需要无线传感器网络中的节点有测距功能,通过节点之间的距离或角度信息,使用三边定位、三角定位或最小最大法等方法计算节点位置。三边定位测量法在计算中没有考虑节点测距误差,若误差过大,可能导致无法定位[4];三角定位测量方法测试次数越多,对位置精度的计算也就越高[5];最小最大法对锚节点的密度只有在较高的情况下定位才准确[6];测距的定位涉及到的算法特征主要有接收信号强度 (Received Signal Strength,RSS)、基于到达时间差(Time Difference of Arrival,TDOA)、基于到达时间(Time of Arrival,TOA)等。另一类为基于非测距的定位算法,如近似三角形内点测试 (Approximate Point-in-Triangulation Test,APIT),若锚节点稀疏则定位精度下降[7];距离向量跳段 (Distance Vector Hop,DVH),不足之处在于计算平均跳距及定位坐标时会产生误差[8],通常非测距算法的实用性差。测距定位成本较低,应用广泛,但是若无线信号受到干扰,则导致测量过程不稳定,定位出现误差,目前解决方法有:最大似然方法(Maximum likelihood method,MIM),通过两次加权进行最小二乘法[9],能够对定位坐标获得较精确数据,但是需要依赖较多的先验知识避免测量误差;交互式多模型-改进卡尔曼滤波(Interacting multiple model-Improved Kalman filter, IMM-IKF), 对非视距误差具有鲁棒性,在未知信道传播状态和非视距误差参数情况下,有效抑制非视距误差,实现高精度定位[10];拟牛顿算法(Quasi-Newton Methods, QNM)方法,通过传统的牛顿迭代法求解[11],但是目标函数具有高非线性,迭代法求解会使定位误差累积,无法获得全局最优解,虽然可以增加参考基站数量来提高定位精度,但基站数量增加使得误差积累同样也增加。在大型传感器网络中通过智能算法进行寻优,解决未知基站坐标的求解问题,主要算法有:粒子群算法(Particle Swarm Optimization,PSO)利用对数障碍函数对目标函数改进,但需要以未知基站的邻站作为必要的参考信息[12],容易陷入局部最优;遗传算法(Genetic Algorithm,GA),通过优化初始种群、自适应调整适应度的选择操作以及加入误差修正算子等方法[13],提高定位算法的性能,但是算法很容易陷入局部最优的问题;链路质量指示 (Link Quality Indicator,LQI)算法,通过改进硬件改善测距精度,再结合粒子群算法改进寻优结果,但没有考虑信道衰减系数变化对量测距离的影响。双阶段位置循环(Two Phase Positioning,TPP)求解算法[14],即启动和细化,启动过程使用HOP模型,细化只涉及节点位于同一跳邻域内,提高了测距精度,但通信量与计算量之间消耗能源较大;粒子群-蚁群算法优化(Particle Swarm Optimization Ant Colony Algorithm,PSOACA),搜寻从距汇聚节点最近的簇头节点出发[15],遍历所有簇头节点,最终到达汇聚节点的最优路径,每个粒子对应于一个簇,只在簇内跳动,并且不重复之前经过的节点,从而实现最小误差。
本文对粒子群算法的惯性权重进行非线性优化,粒子群规模根据粒子的聚集度、多样性函数进行收缩扩张控制,前期快速进行全局寻优,后期缓慢进行局部搜索,最后通过实验仿真对算法的性能进行验证,定性分析相比其他算法具有优势。结果表明本文算法收敛性能较好,相比其他算法能有效地抑制测距误差对定位的影响,能够提高节点的定位精度。
1 基于改进粒子群算法的精准农业无线传感器定位过程
1.1 问题描述
假设网络中存在N个未知节点和M个锚节点[16],节点的坐标集为φ=[φ1,φ2,…,φM+N],锚节点的坐标分别为(x1,y1),(x2,y2),…,(xM,yM),未知节点的坐标为φ=(φx,φy),φx=(xM+1,xM+2,…,xM+N),φy=(yM+1,yM+2,…,yM+N),则定位误差模型为:
(1)
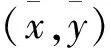
因此,无线传感器网络节点定位问题可转化为约束条件下方程的最优解问题。改进粒子群搜索算法是一种基于全局误差函数的最小化算法,可以利用该算法迭代求解未知节点的位置,减小未知节点坐标的误差,直到获得目标函数的最优值。
1.2 改进粒子群搜索算法
1.2.1 基本粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)通过学习因子c1和c2及惯性权重ω进行更新速度vq,h和位置zq,h:
(2)
式中:q=1,2,…;h=1,2,…;t为迭代次数;vq,h(t)为第q个粒子在第t次迭代中第h维的速度;zq,h(t)为第q个粒子在第t次迭代中第h维的位置;pq,h为当前最优值;pg,h为历史最优值;r1∈(0,1)、r2∈(0,1)为相互独立的随机函数;ω越大越适合在更大的范围内进行搜索,ω越小越能够保证群体收敛到最优位置;c1和c2用于调整粒子飞行,若c1=c2=0, 粒子将一直以当前的速度飞行到边界,一般都设定为2。
1.2.2 惯性权重优化
合适的ω能够控制粒子以往速度对当前速度的影响,平衡全局和局部搜索能力,以较少的迭代次数找到最优解。为了使惯性权重ω适应搜索要求,算法运行初期强化全局搜索能力采用较大的惯性权重,ω递减变化缓慢,后期进行精确的局部搜索采用较小的惯性权重,ω递减变化较快,使用非线性递减(No-Linearly Decreasing Weight,NLDW)策略:
(3)
其中:tmax为最大迭代次数;ωmin=0.35,ωmax=0.95。
1.2.3 收缩扩张控制过程
为避免粒子群聚集在某一特定位置或某几个特定位置现象的发生,能够保持多样性的同时具有较好的收敛率[17],引入收缩扩张因子ε。
粒子聚集度G判别公式为:
G(t)=Pg(t)/avgPi(t)
(4)
式中:avgPi(t)是所有粒子个体极值的平均值;Pg(t)是当前粒子的全局极值。
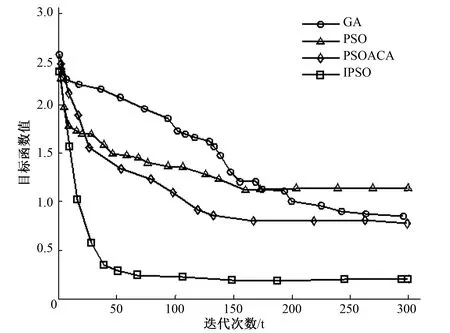
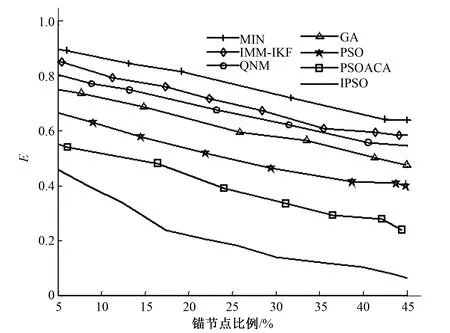
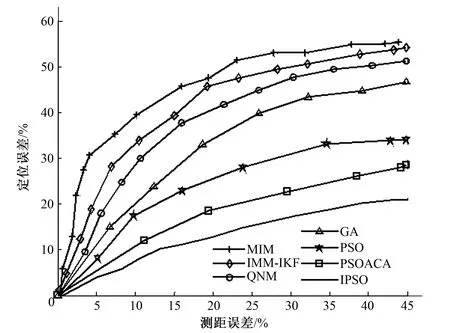
0 (5) 式中:c为粒子总个数;|L|为搜索空间的最长半径;S为问题的维数;Pij为第i个粒子的第j个分量。 算法进化前期需要迅速接近全局极值,故此时收缩扩张系数的值应当处在较大的位置。而在算法进化后期,应减慢速度以加强算法的局部搜索能力,因此收缩扩张系数的值需适当减小,来提高算法的精确度,则ε: (6) 式中:εstart为ε初值;εend为ε终值。 根据惯性权重优化和收缩扩张控制,粒子群的速度vq,h和位置zq,h修正为: (7) 传感器网络中待确定位置节点设置为(x,y),n个参考点的坐标为n1(x1,y1),n2(x2,y2),…,nn(xn,yn),待确定位置节点到参考点距离为di,由于误差,di与计算值不相等,为了减小误差累积[18],适应值函数选择为距离估算值与实际值的均方根误差f(x,y): (8) 式中:(xi,yi)表示第i个参考点坐标;n为目标点邻近参考点数目,n≥3。 由于f(x,y)会将不同节点对应的残差视为同等地位[19],待定位节点的估计位置将倾向于满足残差小的锚节点约束,收敛于真实位置,通过对锚节点区分可信程度,在f(x,y)对未知节点设置不同的权重wi,提高定位精度: (9) 式中:n为未知节点总数;节点u的邻居锚节点ID号为1,2,…;距离测量值分别为du1,du2,…;dul为节点u到邻居锚节点l的距离测量值;duk为节点u到邻居锚节点k的距离测量值;dlk为锚节点l到锚节点k的距离测量值。 则适应度函数选择重新构造为: (10) wi由未知节点到锚节点的距离测量值决定,其关系为反比关系,为避免迭代算法中出现局部最优,控制某个锚节点的损失或所有锚节点的累计损失过大,增设锚节点定位误差阈值与所有锚节点定位误差累积阈值分别为bth、Bth,避免算法陷入局部最优: (11) 这样有效地增强可信锚节点的作用,抑制不可信锚节点的影响。 (1)随机初始化粒子群搜索算法的相关参数,主要包括粒子群总数、速度、位置,其中粒子位置为传感器节点的坐标。 (2)根据公式(10)计算粒子的适应值,得到粒子的pq,h和pg,h,选择当前最优适应值f(xi,yi)所对应的最佳粒子群位置(xi,yi)。 (3)根据公式(7)更新粒子群的位置、速度、pq,h、pg,h,获得新一代粒子位置(xj,yj)。 (4)保留较优的f(xi,yi)与f(xj,yj),并将该适应值对应的粒子群位置记为(x*,y*),(x*,y*)表示当前种群中最优位置。 (5)判断是否满足算法定位精度,若满足,输出全局最优解对应的粒子群位置,否则转至步骤(3)。 选择200 m×200 m的高粱试验场地进行了未知传感器节点定位试验,场地内栽种的大豆植株平均约高30 cm,且植株栽种整齐。将终端监测节点在随机散布于场地中,每个节点拥有相同的通信半径,未知节点和信标节点位置信息随机产生。参数设置如下:初始化粒子总数为120,最大迭代次数为300。 PSO、GA、PSOACA、IPSO算法在精准农业无线传感器定位过程中目标函数适应值的变化曲线如图1所示。 图1 不同算法目标函数适应值变化曲线Fig.1 Variation of fitness function of different algorithm objective function 实验结果表明,IPSO算法的求解速度明显快于其他算法,能够用较少的迭代次数获得更精确的解。这主要是由于IPSO算法使用惯性权重优化、收缩扩张控制,从而能够较好地进行局部、全局搜索,避免搜索的单一性,IPSO增加了PSO算法收敛速度和全局收敛性,最终收敛得到最优解,能够使无线传感器获得精确定位。 归一化平均定位误差评价指标E[20]: (12) 归一化平均定位误差与消耗时间的对比关系如图2所示,涉及的算法有MIM 、IMM-IKF、 QNM、PSO、GA、PSOACA、IPSO。 图2 归一化平均定位误差与消耗时间的关系Fig.2 Relationship between normalized mean location error and consumption time 从图2可以看出,随着消耗时间的增加,各种归一化平均定位误差都逐渐下降,但是IPSO消耗时间明显优于其他定位算法,在1 s时刻即可获得较低的定位误差,在3 s左右开始保持不变,表明该算法具有很强的稳定性,而且具有很高的定位精度。 图3为各种算法在锚节点数量不同的情况下的归一化平均定位误差。 图3 锚节点个数对定位性能的影响Fig.3 Influence of anchor node number on positioning performance 从图3可以看出,随着锚节点比例不断的增大,各种算法的平均定位误差都逐渐减小,并逐渐趋于稳定。在相同锚节点比例情况下,IPSO算法优化后的平均定位误差更小,这说明IPSO算法在少量的锚节点的情况下,能取得较好的定位效果。 图4为各种算法的定位误差随着测距误差变化的曲线。 图4 定位误差随着测距误差变化曲线Fig.4 Location error versus range error curve 从图4可以看出,随着测距误差的增加,各种算法定位误差都呈上升的趋势。但是,相对于其他算法,IPSO算法受测距误差的影响相对较小,能够在一定程度上抑制节点测距误差的累加;当测距误差比较大时,IPSO算法的定位效果更加稳定。说明IPSO算法优化定位有着更好的抗误差性。 本文算法对粒子群算法优化主要包括惯性权重参数、群体规模收缩扩张控制,惯性权重参数采用非线性方法,即算法运行初期强化全局搜索能力采用较大的惯性权重,后期进行精确的局部搜索采用较小的惯性权重,提高群体算法对起始锚节点的精确度;群体规模收缩扩张控制算法前期群体规模扩张操作,后期收缩操作,提高算法对锚节点的稳定性,仿真实验结果表明,本算法获得了较好的定位效果,能够提高网络工作效率、优化网络性能,降低农业生产成本,为农业智能化研究提供了新的思路和方法。
1.3 适应度函数选择
1.4 算法流程
2 实验仿真
2.1 收敛性能对比
2.2 定性分析
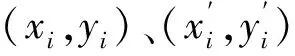

2.3 锚节点个数对定位性能的影响
2.4 测距误差对定位性能的影响
3 结 语
