城市背景下草地蒸散发及土壤水分变异特性----以扬州区域性草地植被为例

周 钦，黄金柏，周亚明，黄涌增

(扬州大学水利与能源动力工程学院，江苏 扬州 225127)

城市化是当今世界发展的重要特性，任何一个国家或地区的发展都离不开这一变革，但同时它也会带来相应的生态、气候问题[1]。在城市化进程中，大量建筑物的建造导致原有的裸露地面、植被等被不透水或弱透水地面所覆盖的面积不断增加，城市在暴雨时易造成排水不畅、形成地面积水的局面。同时，城市扩展在很大程度上改变了城市下垫面的热力性质和动力性质[2]，不仅对区域内的气温、降雨等气候因素产生影响[3]，使城市产生热岛效应、雨岛效应，也影响着水文过程中蒸散发的变化[4]。蒸散发是水文循环中重要的环节，是土壤水分和大气层水分之间交换的媒介[5,6]，对其进行定量估算是评价区域耗水及土壤水分运移的基础[7]。在城市化背景下，海绵城市理念越来越受到人们的关注。运用海绵城市理论，增加绿地植被，能够有效加快雨水入渗，提高土壤的蓄水功能，从而能降低城市的洪涝灾害风险，改善提升城市的生态水平[8]。

扬州市地处江苏省西部，江淮下游，属北亚热带湿润气候区[9]，年平均气温为15～18℃，多年平均降雨量达1 000 mm，且大部分降雨集中在5-9月[10]。相对集中的汛期对浅层地下水位带来显著的变化的同时可能造成城市内涝。近年来，扬州城市化发展加快，人口不断增加，绿色植被逐渐减小。为揭示扬州城市化背景下草地植被蒸散发和土壤水分的季节性变化特性，本文选取扬州大学扬子津校区农水与水文生态实验场及扬州大学江阳中路南校区草地植被为研究区，对气象数据以及土壤水分进行观测，利用原始的彭曼-蒙蒂斯(Penman-Monteith)公式估算草地蒸散发量ET，利用FAO推荐的经修正的彭曼-蒙蒂斯(Penman-Monteith)公式估算参考作物蒸散发量ET0，并推求草地植被的水分有效性参数。通过构建研究区小尺度土壤水分运动模型，对表层土壤水分进行模拟，研究结果以期为扬州城市化背景下草地植被的水分循环和基于发展绿色植被提升海绵城市建设水平提供部分基础数据。

1 研究区概况及数据观测

1.1 研究区概况

选取扬州大学扬子津校区农水与水文生态实验场气象站内草地P1(32°21′14.95″N，119°23′46.32″E)及扬州大学江阳路南校区草地植被P2(32°22′53.64″N，119°25′8.15″E)为研究区，两点的写真如图1所示。

图1 研究区P1、P2写真

1.2 数据观测

通过在P1、P2设置气象站(型号：U30-NRC-10-S100-000；制造商：美国OnSet仪器设备公司；观测点高程：14 m)对主要气象数据如温度、风速、相对湿度、太阳辐射量、降雨量等进行观测；利用土壤水分计(型号：H21-002； 制造商：美国OnSet公司)对地面以下5、15及30 cm处的土壤水分进行观测。 数据观测的时间间隔均为1 h，观测时段为2016年10月5日至2017年10月4日。在观测时段内，不同深度的土壤水分数据存在时段性的缺失。

2 材料和方法

2.1 蒸散发计算

蒸散发是水循环的重要组成部分，也是水文模型的关键输入因子[11]。蒸散发的准确推求，对进一步了解土壤水分运移及评价区域耗水具有重要意义[12]。本研究采用由联合国粮农组织(FAO)推荐的经修正的彭曼-蒙蒂斯(Penman-Monteith)公式计算参考作物的蒸散发量ET0，采用彭曼-蒙蒂斯(Penman-Monteith)公式计算草地生长期的蒸散发量ET。采用ET与ET0的比值作为水分有效性参数(ma)，用来评价研究区水分有效性的季节变化。

(1)

(2)

ma=ET/ET0

(3)

式中：ET0为参考作物蒸散发量，mm/d；Δ为饱和水汽压与温度函数曲线在某时间点上的斜率，kPa/K；Rn为地表净辐射量，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；es为不同温度的饱和水汽压，kPa；ea为实际的水汽压，kPa；T为空气温度，℃；u为风速，m/s；γ为干湿温度计常数，kPa/K；ET为草地蒸散发量，mm/d；ρ为空气密度，kg/m3；ra为气动阻抗，s/m；rs为表面阻抗，s/m；cp为空气比热，1.0×10-3MJ/(kg·K)；l为水的汽化潜热，MJ/kg。式(1)、(2)中各因子的计算方法由式(4)～(13)进行确定。

(4)

(5)

γ=0.665×10-3P

(6)

(7)

l=2.50-0.002 4T

(8)

(9)

(10)

z0m=0.123Hc

(11)

z0h=0.1z0m

(12)

式中：P为大气压强，kPa；Hc为作物高度，计算时为草地植被覆盖下的植物平均计算高度，取0.12 m；d为零平面置换高度，m；z为气象观测高度，m；z0m为动量传递的粗糙长度，m；z0h为热和水汽的粗糙长度，m；k为von Karman’s常数(0.41)。

利用公式(2)，基于0～30 cm的平均土壤水分θ的变动过程来率定表面阻抗rs[13]，近似的得到土壤水分θ与表面阻抗rs的关系函数如下：

rs=26 498 exp(-4.784θ)

(13)

式中：θ为表层土壤平均含水量，cm3/cm3。

2.2 土壤水分模型的构建

2.2.1 基础方程式

利用Richards方程构建研究区一维土壤水分运动模型，如下：

(14)

式中：θ为土壤体积含水量，cm3/cm3；t为时间因子；z为垂向空间因子；D(θ)为土壤水分扩散率，cm2/d；K(θ)为土壤导水率，cm/d。

2.2.2 算法建立

为了保证求解的精度，采用有限差分方法来对所建立的土壤水分运动方程进行数值算法的拟定。利用有限差分方法，对式(15)在时间和空间上进行离散，以1 d为时间步长(Δt)，垂向取10 cm(Δz)的土壤为第一层，对其土壤含水量进行计算。差分格式如下：

(15)

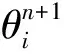
2.2.3 参数率定

为了实现模型参数的准确率定，对两点土壤进行多次采样，并进行物理性分析。分析的主要内容为土壤的机械组成及土壤物性，根据实验结果推求出土壤密度、土壤孔隙率等土壤物理性参数，实现模型中基本参数的确定；通过简易渗透实验，推求出土壤水分的垂向渗透系数[15]；利用激光粒度分析仪(Mastersizer 3000E)筛选土壤颗粒级配(黏粒、粉粒、砂粒的百分含量)并通过美国农业部土壤质地分类三角坐标图分析研究区土壤质地(粉壤土)[16]。最终确定的模型主要参数及颗粒级配如表1所示。

3 结果及分析

3.1 蒸散发计算结果

参考作物蒸散发计算时段为2016年10月5日至2017年10月4日。由图2可以看出，P1、P2两点ET0曲线几乎重合，计算时段内，两点的年ET0为1 115.0 mm(略低于年降雨量1 200 mm)，均值为3.0 mm，最小值发生在2016年12月26日，为0.2 mm，当日温度仅为7 ℃，太阳辐射量为8.7 W/m2；最大值发生在2017年7月16日，约为7.7 mm，当天温度高达33.6 ℃，太阳辐射量为258 W/m2。从全年来看，ET0的季节性变化趋势明显，12月至2月两点的ET0多在0.1～3.0 mm/d之间，变动幅度较小，处于全年较低水平，其主要原因是在此期间，影响蒸散发量的主要气象因子温度、太阳辐射量、风速等在一年内都处于较低水平；5-9月两点的ET0变化范围大部分处于2.0～8.0 mm/d之间，变动幅度较大，处于全年较高水平，主要原因在于上述气象因子在一年中高于其他月份，且水分供应也较充足。

图2 P1、P2参考作物蒸散发(2016-10-05-2017-10-04)

图3 P1、P2生长期内蒸散发量(2017-07-01-2017-09-30)

由于部分土壤水分数据缺失，ET计算时段为2017年7-9月，该时段处于草地植被的生长期内，在时间上占据了当地雨季(6-9月)的大部分时间。ET的计算结果如图3所示，计算时段内，两点的日平均蒸散发量在1.4 mm/d左右，P1点ET计算结果最大值为4.4 mm/d(2017-09-16)，最小值为0.05 mm/d(2017-09-24)，在此计算时段内，草地的总蒸散发量为129.7 mm，占同期降雨量的24.2%；P2点ET计算结果最大值为4.4 mm/d(2017-09-16)，最小值为0.05 mm/d(2017-09-24)，草地的总蒸散发量为122.2 mm，占同期降雨量的22.9%，两点的蒸散发量约占同期降雨量的1/4。

蒸散发不仅受外界环境的影响，还受控于土壤水分的含量。草地蒸散发ET对集中降雨的反应很灵敏，在集中降雨发生后，ET常会出现较大的值，其原因是雨后土壤含水量较高，且对蒸散发有较大影响的气象因子常处于较高水平，如气温较高、太阳辐射量集中等，所以ET显著。在计算期内的大部分时间点上，P2的ET略低于P1的ET，原因在于P2的表面阻抗rs高于P1，而表面阻抗受土壤水分含量的影响，土壤含水量越小，表面阻抗越大。因此土壤含水量的大小决定了蒸散发过程中可用于蒸散发的水分状况。

3.2 水分有效性评价

将同期ET和ET0的比值定义为水分有效性参数(ma=ET/ET0)，用来评价研究区的水分有效性。图4所示为计算时段内P1、P2ma的变化情况。ma的曲线形状与ET曲线形状相似，主要受ET的影响。ma处于0.02～0.94之间，最小值为分别为0.03、0.02，均发生于8月1日，当日风速处于计算时段内的最大值(3.3 m/s)，由于长时间没有降雨，且因强烈的蒸发作用，土壤水分含量较低；ma最大值分别为0.94、0.93(ET分别为0.88、0.86，ET0为0.93)，均发生于9月27日，由于当天的降雨强度较大，土壤含水量显著增加，较高的土壤含水量为蒸散发提供了相对充足的水分，从而导致当日的蒸散发量与潜在蒸散发量接近。

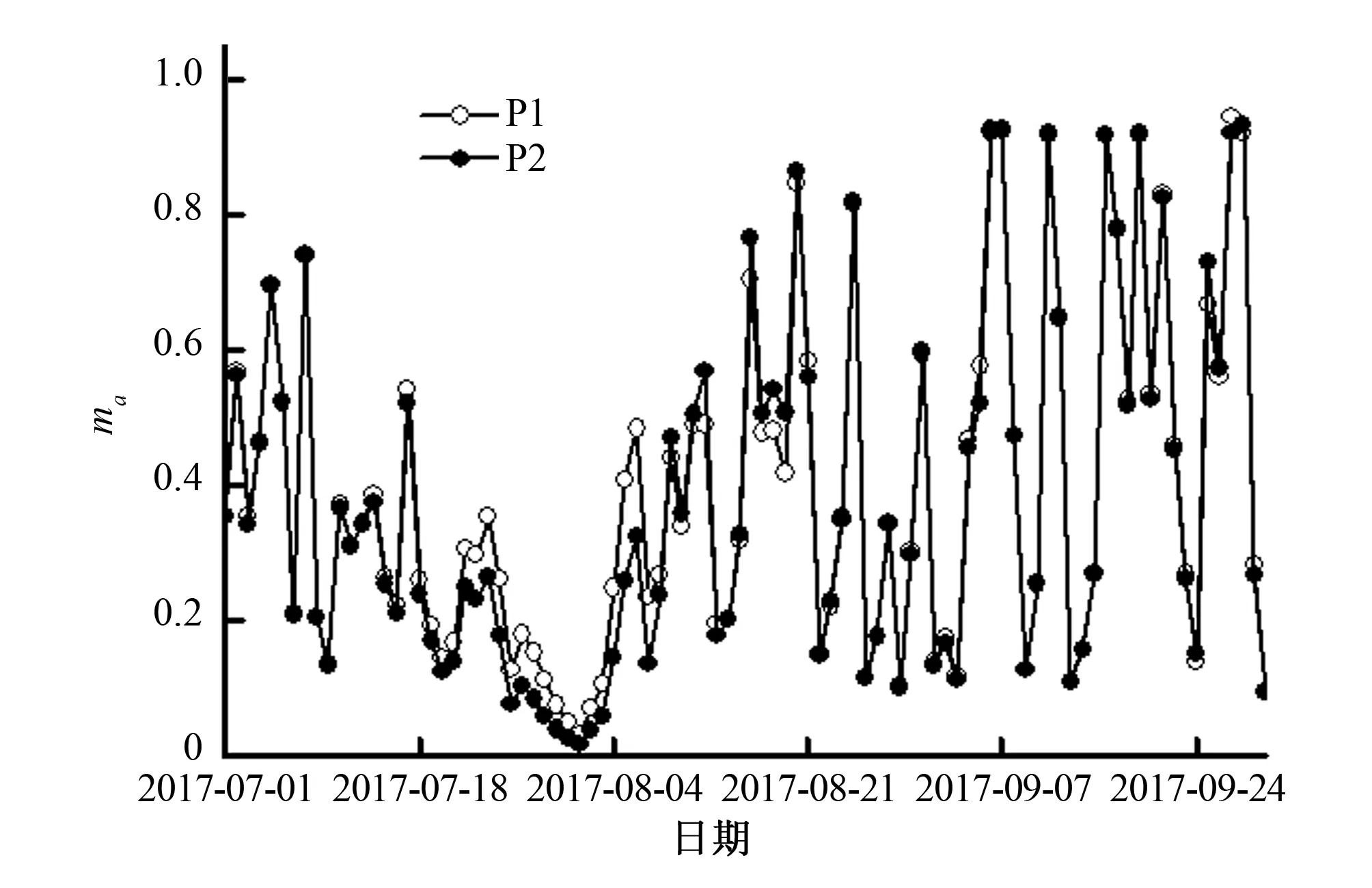
图4 P1、P2水分有效性参数ma(2017-07-01-2017-09-30)

在8、9月份，ma多处于较高水平，原因在于雨季的降雨量相对集中，土壤中的雨水入渗量增加，同时气象因子中对蒸散发产生主要影响的气温、太阳辐射量都处于较高水平，导致ET较大，在这些时刻，ma也出现较大的值。由此可知，ET的变化影响着水分有效性参数ma的变化。计算时段内，P1、P2两点的ma平均值分别为0.39、0.37，P1点略高于P2点。

3.3 土壤水分模拟结果

由图5、图6可知，7-9月的降雨量为536.5 mm，占全年降雨量的44.7%，最大一次降雨发生在9月24日(降雨量：101.2 mm)。土壤含水量对降雨的反应很灵敏，在集中降雨发生期间，表层土壤含水量在短时间内显著增加(9月24日)，含水量峰值出现时间与降雨时间有很好的一致性；在无雨或少雨的情况下，土壤水分含量呈逐渐降低的趋势。

计算时段内P1、P2土壤水分模拟结果曲线分别如图5、图6所示。计算时段内两点表层土壤含水量(0～10 cm)实测值与计算值曲线之间的契合度很高，模拟值很好地再现了土壤水分观测值的变化过程。在无降雨时段，土壤水分的计算值与实测值之间的绝对误差很小，仅在±0.02范围以内，且计算值一般小于实测值；降雨产生阶段，计算值与实测值之间的误差波动较大，绝对误差在±0.05之间，原因在于模型仅考虑了土壤水分的垂向收支过程，当表层土壤含水量较高时，水分会发生横向扩散，从而对计算点的模拟精度产生较大影响。

图5 P1点第一层土壤水分模拟结果(2017-07-01-2017-09-30)

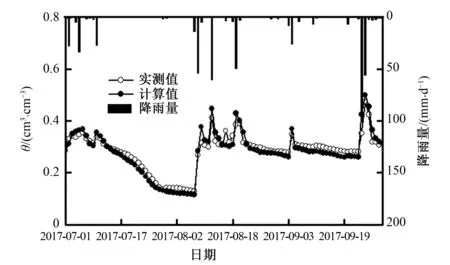
图6 P2点第一层土壤水分模拟结果(2017-07-01-2017-09-30)

3.4 模型检验

利用均方根误差(RMSE)及纳什效率系数(NSE)对模型的实用性及效率等加以检验。RMSE是用来评价模型的计算精度，此值越接近于0，表示模型的模拟精度越高；NSE表示模型运行效率的高低，此值越接近于1，表示模拟结果越接近观测结果，模型可信度高。

(16)

(17)

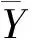
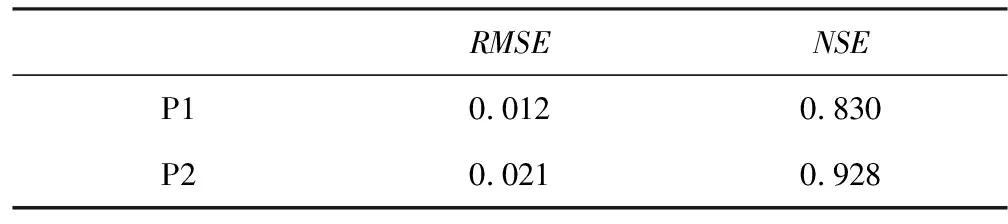
表2 模型检验参数值

由表2可知，P1、P2两点表层土壤水分的实测序列与计算序列的均方根误差(RMSE)分别为0.012、0.021，显示出模型的可靠性，能较好地模拟不同下垫面土壤水分动态变化过程；从纳什效率系数(NSE)来看，P1点的NSE为0.830， P2点的NSE为0.928，模型运行效率较高。

4 结 语

本文选取扬州大学扬子津校区农水与水文生态试验场(P1)与江阳中路南校区草坪(P2)为研究区，推求了潜在蒸散发量(2016-10-05-2017-10-04)、草地蒸散发量(2017-07-01-2017-09-31)并对水分有效性进行了评价，构建了一维表层土壤水分模拟模型并对模型的实用性进行检验，得出主要结论如下。

(1)2016年10月5日至2017年10月4日， P1、P2的年ET0累积值为1 115.0 mm，略低于同期降雨量，且具有明显的季节性变化；2017年7月1日至2017年9月30日，P1、P2的ET累积值分别为129.7、122.2 mm，略低于同期降雨量的25%；同期P1、P2的水分有效性参数(ma)分别为0.39、0.37。

(2) 构建的一维土壤水分计算模型的RMSE小于0.025，NSE在0.80以上，说明模型的计算精度较高且具有较高的运行效率。

研究成果以期为城市化背景下草地植被的土壤水分循环及土壤水分的继续研究提供研究基础。