农田土壤入渗不确定性组成分析

范欣瑞，王仰仁，孙小平

(1.天津农学院水利工程学院，天津 300384；2.天津市节水灌溉技术与装备校企协同创新实验室，天津 300384；3.山西省水利水电科学研究院，太原 030002)

0 引 言

土壤入渗过程[1]决定着降水或灌溉水进入土壤的速度。不仅关系到对当季作物的供水量，而且还关系到供水以后或来年作物利用的深层水的贮量。地表径流是引起水土流失的直接原因，因此，土壤入渗研究对于降雨径流调控、水土保持、水资源评价管理、农田灌溉技术参数确定等都具有重要意义[2]。在入渗规律的研究和应用中发现不同空间点同一时间的累计入渗量是不相同的，其稳定入渗速率也有较大差异，采用入渗模型拟合的参数也不相同，模型拟合残差随时间有明显变化。这种差异是由土壤结构的空间变异等因素引起的，将其称为入渗的不确定性。这些不确定性变化特征主要表现为随机性、未确知性，通常采用随机模拟方法(以均方根误差为评价指标)进行分析[3,4]。

目前国内土壤入渗模型的研究已较为广泛，总体分为三类：基于物理意义的半理论半经验模型(包括Green-Ampt模型、Philip模型等)和纯经验模型(包括Horton模型、Holtan模型、Kostiakov 模型、修正的Kostiakov 模型等)[5,6]。土壤入渗模型在农田土壤水分的动态变化过程基础上对入渗规律进行模拟，作为自然过程的数学表达，模型不可避免的要进行假设和简化，因此模拟的结果不可避免的会带来不确定性[7]，故需要对模型结构进行合理评价[8]。

许多学者通过比较不同土壤入渗模型的参数及入渗模拟结果，确定适合不同区域尺度的土壤水分入渗模型。徐海芳等依据大田试验研究了 Horton 模型和Philip模型，系统分析了模型中各参数的概率分布和统计特征值(均值，变异系数)，得出各参数的变化规律，从而确定Horton 模型为适合当地的土壤水分入渗模型[9]。Machiwal等基于Philip、Green-Ampt和Kostiakov模型对土壤入渗过程的模拟效果进行显著性分析，发现 Philip 模型的拟合效果最佳，在此基础上对Philip 模型进行了标定，确定了最优标定因子[10]。

对于土壤入渗的空间变异性已有所研究，刘泓志等人利用地统计学方法对降水入渗补给系数的空间变异特征进行了分析[11]，何锦等人在华北平原中等区域尺度下研究了土壤入渗特征参数的空间变异性[12]。另外模型结构也存在一定程度的不确定性[13,14]。牛文全等利用室内土柱试验，以95%后验置信区间上下限的差值和标准差为指标，评价了残膜对湿润锋运移、累积入渗量、累计蒸发量及其不确定性的影响[15]。本研究基于Kostiakov-lewis 、Philip 、Horton三种模型，采用四个测点的入渗资料，分析研究了农田入渗的不确定性。该研究可为农田尺度上土壤入渗的模拟提供依据。

1 材料与方法

1.1 试验区概况及入渗测试方法

试验田位于天津市武清区东北部的崔黄口镇北靳庄村。该地区有较好的灌溉条件，水源从永定新河引入沟渠，再提水灌溉，小麦生育期一般灌水2～3次，玉米生育期灌水一般1～2次，全村耕地154.67 hm2。该地区多年平均气温12.2 ℃，多年平均降雨量为557.3 mm左右，蒸发量1 735.9 mm。土壤质地为中轻壤土，0～100 cm土壤平均干容重1.41 g/cm3，田间持水率24.6%，地下水埋深4～5 m。

本试验选取两个大田地块(每个地块15 m×80 m)，每个地块上选取两个点，共四个测点，具体布置如图1；采用双环入渗仪(内环直径30 cm，外环直径60 cm，内外环高度均为25 cm)测定土壤水分入渗过程，具体分为四步：平整土地(除去地表植被及石块等)、安置铁环(内外环先后垂直置入土中10 cm，内外环同心)、水位测试标记(紧靠内环内壁插入钢尺，离土壤表面5 cm处做标记)以及加水计时(内外环维持同样水头5 cm，当水深下降1 cm时及时加水，并记录加入水量和时间，当相邻加水间隔时间接近时便可结束试验)。

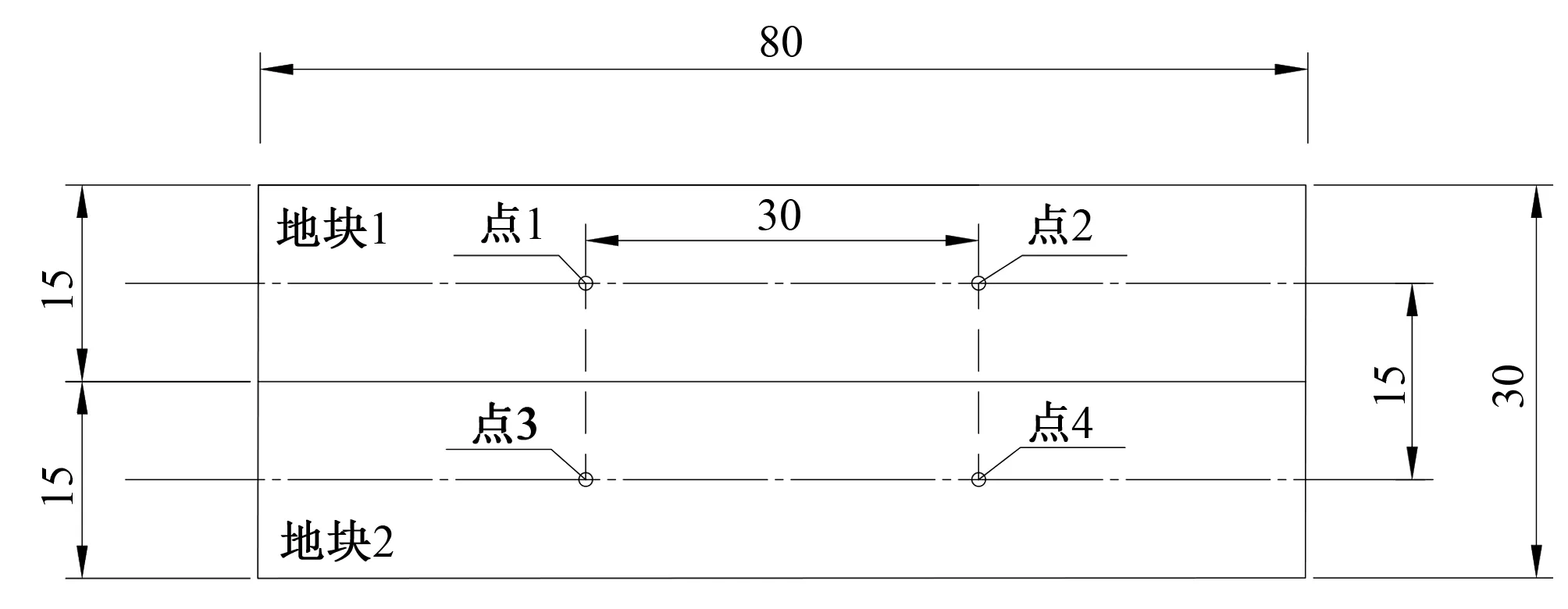
图1 入渗试验点平面布置图

1.2 分析方法

1.2.1 入渗模型及参数确定

本文选用Kostiakov-lewis、Horton和Philip模型三种常用的土壤入渗模型进行入渗量的模拟。

(1)Philip模型。Philip(1957)利用级数法对入渗问题进行求解，在得出垂直入渗级数解的基础上取前两项近似描述入渗变化规律，见式(1)[16]：

(1)

式中：I为累积入渗量，mm；i为渗透速率，mm/min ；t为入渗时间，min；S表示土壤吸渗率，A为稳渗率，A、S的值可通过入渗试验得到。该公式物理意义明确，公式简单，且参数易于确定。

(2)Kostiakov-lewis 模型。Kostiakov-lewis 模型(1937)表示的土壤水入渗过程中累积入渗水量随时间的变化关系：

I=Ktα+f0t

(2)

式中：K为经验入渗系数；α为入渗经验指数，表示土壤入渗的衰减速度；f0为土壤相对稳定入渗率,mm/min。其余符号意义同前。

(3)Horton模型。Horton模型(1940)表示的土壤累积入渗速率随时间的变化关系如下，

i=ic+(i0-ic)e-β t

(3)

式中：i0为t=0时的初始入渗率；ic是稳定入渗率；β为描述入渗过程中入渗速率降低的参数。

对式(5)积分可求得土壤累积入渗水量随时间的变化过程：

(4)

Horton公式是纯经验公式，但其参数具有较为明确的物理意义，结构简单，得到了广泛应用。

观察公式可以看出，Philip模型属于线性模型，可采用二元线性回归分析的方法确定其参数，Horton和Kostiakov-Lewis模型是非线性模型，其参数拟合属于非线性规划问题。利用最小二乘法[目标函数见式(5)]对参数进行拟合时，其中的参数ic、i0和f0的初始值可通过其物理意义确定，但是参数K、α和β因为不具有明确的物理意义，拟利用泰勒级数对公式进行展开，结合田间实测入渗数据，获得初始值，再利用EXCEL中的规划求解工具进行拟合，即可得到最优入渗模型参数[17]。

(5)

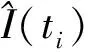
1.2.2 农田土壤入渗不确定性组成

农田土壤入渗过程中，在严格按照入渗测试要求条件下，入渗数据与模拟曲线之间仍然会有不同程度的偏离，该偏离的程度可用拟合误差表示，或者用均方根误差表示。该偏离值可用于表示入渗随时间变化的不确定性。其产生的原因主要是，土壤质地和结构随深度有所变化。

拟合误差的值[式(6)]，在一定程度上反映了该类农田土壤随时间变化的不确定性程度。对于同一点而言，入渗模型拟合误差越小，表明该模型对土壤入渗特性解释程度越好，不确定性也就越小。

(6)

式中：q(ti)表示累积入渗量的模拟值与实测值之间的残差值，mm；其他符号意义同前。

农田土壤入渗空间不确定性可用土壤入渗数据的均方根误差[式(7)]表示，其值可通过分析农田不同空间点土壤入渗试验资料确定。入渗模型的结构也包含了不确定性，可用不同模型模拟值的均方根误差间的差异来表示。

(7)

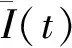
2 结果分析

2.1 参数拟合结果

分析大田试验四个测点的土壤入渗数据，对三种模型进行拟合分析，可得模型参数拟合结果(见表1)。

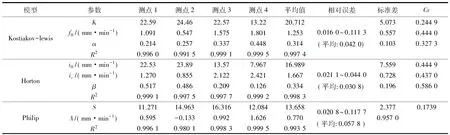
表1 入渗试验的模型拟合分析

模型拟合结果的统计分析(见表1)表明，Horton模型累积入渗量模拟值和实测值的平均相对误差最小(3.1%)，Philip模型对应的平均相对误差最大(5.8%)；各模型参数的Cv值介于0.173 9～0.957 0，标准差介于0.103～7.559。从模型拟合的相关程度来看，Horton模型的相关系数(R2)值最大，四点平均值达0.998 3，Philip模型较小；但总体都在0.99以上，相对误差介于1.60%～11.77%，表明各模型对于农田入渗规律模拟的可靠性均较高。

2.2 不确定性组成分析

图2(a)、(b)和(c)分别给出了基于3种模型、四组累积入渗量(编号(i)表示第i个测点，i=1,2,3,4)的模拟值和实测值间残差随时间呈现波动的变化过程，反映了农田土壤入渗的时间不确定性(残差)。3种模型对应时间不确定性随着入渗时间增加快速减小，在入渗20 min之后围绕一个不随时间变化的稳定水平上下波动，变化于0.021 8～16.228 mm之间。同时图中给出了4个测点实测累积入渗量均方根误差(STDEV)随时间的变化过程，反映了整个入渗过程中不同空间点累积入渗量的变异，即入渗过程的空间不确定性。由此可见，空间不确定性(STDEV)随入渗时间呈线性增加，由入渗初的5.674 mm增加到150 min时的107.532 mm。从图2中可看出，在入渗初期(0～20 min)，时间不确定性略大于空间不确定性，入渗后期(20 min之后)，时间不确定性要远小于空间不确定性。

图3给出了3种模型针对4个测点模拟值的均方根误差(STDEV)随入渗时间的变化曲线。由图3可见，3个模型对应曲线不重合，表明模型结构也会产生不确定性；Kostiakov-Lewis模型对应STDEV从入渗初期(5 min)的4.720 mm变化到入渗后期(200 min)的138.452 mm，Horton模型对应STDEV从入渗初期的6.781 mm变化到入渗后期(200 min)的147.282 mm，Philip模型对应STDEV从入渗初期的5.522 mm变化到入渗后期(200 min)的141.387 mm。3个模型的STDEV均随时间呈递增趋势，且随入渗时间的增加，3个模型的STDEV值间的差异逐渐增大。

为了量化模型结构造成的不确定性，表2给出了入渗过程中不同模型对应5、30、90和150 min 4个入渗时间STDEV值。

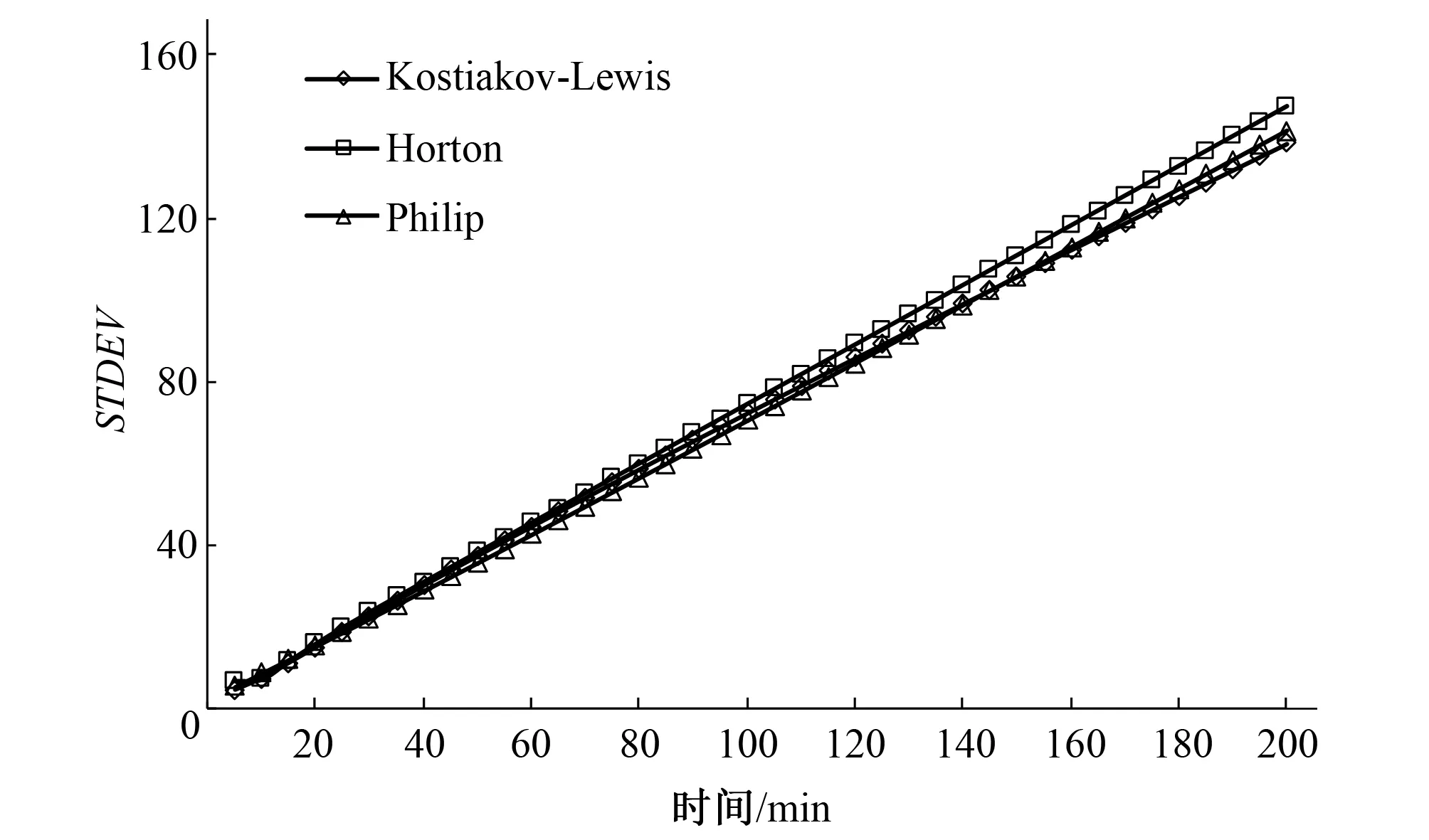
图3 3种模型模拟值的STDEV随入渗时间的变化曲线

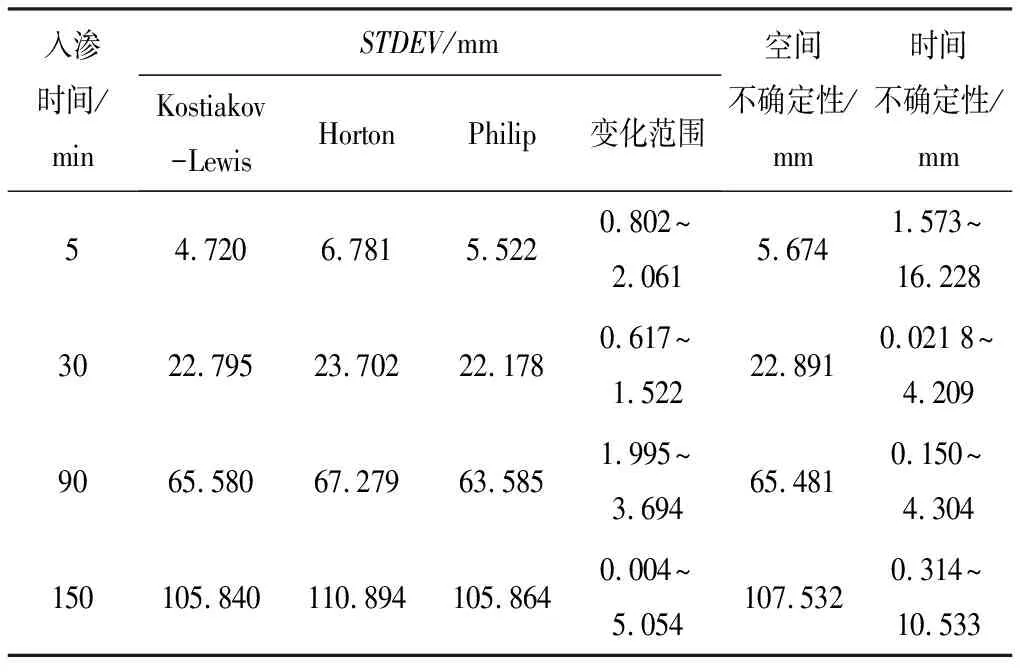
表2 模型结构不确定性分析

从表2可看出，入渗5 min时对应三个模型间的差异介于0.802～2.061 mm，相应时间不确定性为1.573～16.228 mm，空间不确定性为5.674 mm；入渗30 min时对应三个模型间的差异介于0.617～1.522 mm，相应时间不确定性为0.021 8～4.209 mm，空间不确定性为22.891 mm；入渗90 min时对应三种模型间的差异介于1.995～3.694 mm，相应时间不确定性为0.150～4.304 mm，空间不确定性为65.481 mm；入渗150 min时对应三种模型间的差异介于0.004～5.054 mm，相应时间不确定性为0.314～10.533 mm，空间不确定性为107.532 mm；总体而言从入渗5 min到150 min入渗期间，模型结构不确定性的变化范围为0.004～5.054 mm，时间不确定性的变化范围为0.021 8～16.228 mm，空间不确定性的变化范围为5.674～107.532 mm。整体而言，不确定性对农田土壤入渗过程影响的程度：空间不确定性>时间不确定性>模型结构不确定性。

3 结 语

(1)对实测数据的拟合分析结果表明，Horton模型的相关系数最高，Philip模型和Kostiakov-Lewis模型次之，三者相关系数差别很小，均可用于该试验区田间土壤入渗模拟。

(2)在农田尺度的土壤入渗模拟过程中，存在时间不确定性、空间不确定性以及模型结构的不确定性，时间不确定性在入渗初期有一个快速减小的过程，之后呈现趋于稳定的波动过程；空间不确定性随时间呈线性增加趋势；模型结构不确定性随时间有缓慢递增趋势。

(3)对比分析三种不确定性因素的影响表明，空间不确定性对土壤入渗过程产生的不确定性最大，时间不确定性次之，模型结构的不确定性最小。