基于MATLAB似大地水准面精化的区域应用

封华梅

(陕西省一八五煤田地质有限公司，陕西 榆林 719000)

0 引言

似大地水准面指的是从地面点沿正常重力线量取正常高所得端点构成的封闭曲面，与大地水准面的差值为正常高与正高之差[1]。大地高与正高或正常高之间的差距，分别称为大地水准面差距和高程异常[2]。求解大地水准面差距或高程异常的主要方法有几何法[3]、重力法[4]及组合法等[5]。利用GNSS/水准拟合法是几何确定似大地水准面的一种方法，其中多项式拟合是建立拟合模型的一种。其原理就是在区域范围内的GNSS网中，存在若干个联测了水准高程的GNSS点(称GNSS水准重合点)，根据GNSS水准重合点上已知的大地高和正常高确定GNSS水准重合点上的高程异常，然后再由GNSS水准重合点的平面坐标与高程异常的函数关系构造某一曲面来逼近似大地水准面，进而推算出测区中未进行水准联测的GNSS点的高程异常，从而得到测区内所需GNSS点的正常高[6]。

1 函数模型理论

函数模型拟合的最大优点是对于趋势性变化的拟合效果较好，但需要合适的函数模型形式，并需要确定合适的参数个数。若函数模型的针对性强，则拟合与推估的效果好。函数模型的形式一经确定，计算过程中一般不再变化。基于选定的函数模型及其相应的拟合原则，很容易求得模型中的待估参数，如此即完成了函数模型的构造与拟合。基于拟合的函数模型，即可求解未知点的信号。然而，任何待定的模型均难以“准确”地表征逼近场的一切特征。于是难免有部分“剩余误差”；另一方面，任何函数模型逼近均基于足够的已知点信息，这类已知信息的任何误差都将对函数模型的待估参数的估计带来影响。这种影响又必将对后续未知点值的推估带来误差[7]。

1.1 多项式拟合模型

多项式函数的数学模型是

ξ(x，y)=F(x，y，β)

(1)

式中:ξ(x，y)—点(x，y)处的高程异常值；F(x，y，β)—所选择的函数形式。

将(1)式表示成

ξ(x，y)=a0+a1x+a2y+a3x2+a4y2+a5xy

(2)

式中:a0～a5—待定系数。

通常采用较多的模型是二次多项式模型，以此推导平差过程：

利用公共点上GNSS测定的大地高和水准测量的正常高计算出该点上的高程异常，若测区内有n(n>6)个这样的公共点，则可算出高程异常ξi(i=1，2，…，n)，根据模型可以列出n个误差方程

(3)

写成矩阵形式为

V=BX-L

(4)

其中：

V=[v1v2…vn]T

X=[a0a1a2a3a4a5]T

L=[ξ1ξ2…ξn]T

根据最小二乘法原理VTPV=min可得

X=(BTB)-1BTL

(5)

就可解算出拟合方程的待定系数，然后根据模型解算出未知点上的高程异常值。

1.2 GNSS/水准拟合的精度分析

目前GNSS/水准拟合的精度主要通过内符合精度和外符合精度来评定[8]。

内符合精度：根据参与拟合的已知点的实测高程异常ξi与拟合高程异常ξ＇i的差值vi进行计算，若参与拟合的已知点数为n，则内符合精度σ内为

(6)

外符合精度:根据检核点的实测高程异常ξi与拟合高程异常ξ＇i的差值vi进行计算，若检核点的数为m，则外符合精度σ外为

(7)

2 基于MATLAB程序的实例分析计算

为了分析GNSS/水准拟合法在实际生产中应用的可靠性，在此将利用小保当煤矿工业广场和风井广场的实测控制点进行验证分析，采用以下评定精度的标准：最小拟合误差Vmin、最大拟合误差Vmax、内符合精度σ内、外符合精度σ外。

2.1 测区概况介绍

该区域位于小保当煤矿工业广场和风井广场之间，形状为长方形，东西长约3.6 km，南北宽约1.4 km，面积约5 km2。本区域西高东低，局部均相对平坦。在该区域均匀分布GNSS/水准重合点21个，在相对独立坐标系的成果见表1。

2.2 参与计算的已知点选取

根据选点原则，在测区均匀选择部分GNSS/水准重合点进行参与计算，通过分析选择XG02、XG03、XG04、XG05、XG06、XG07、XG08、XG10、XG11、XG12、XGJ8、YF04、YF06、EF03等14个点参与计算。

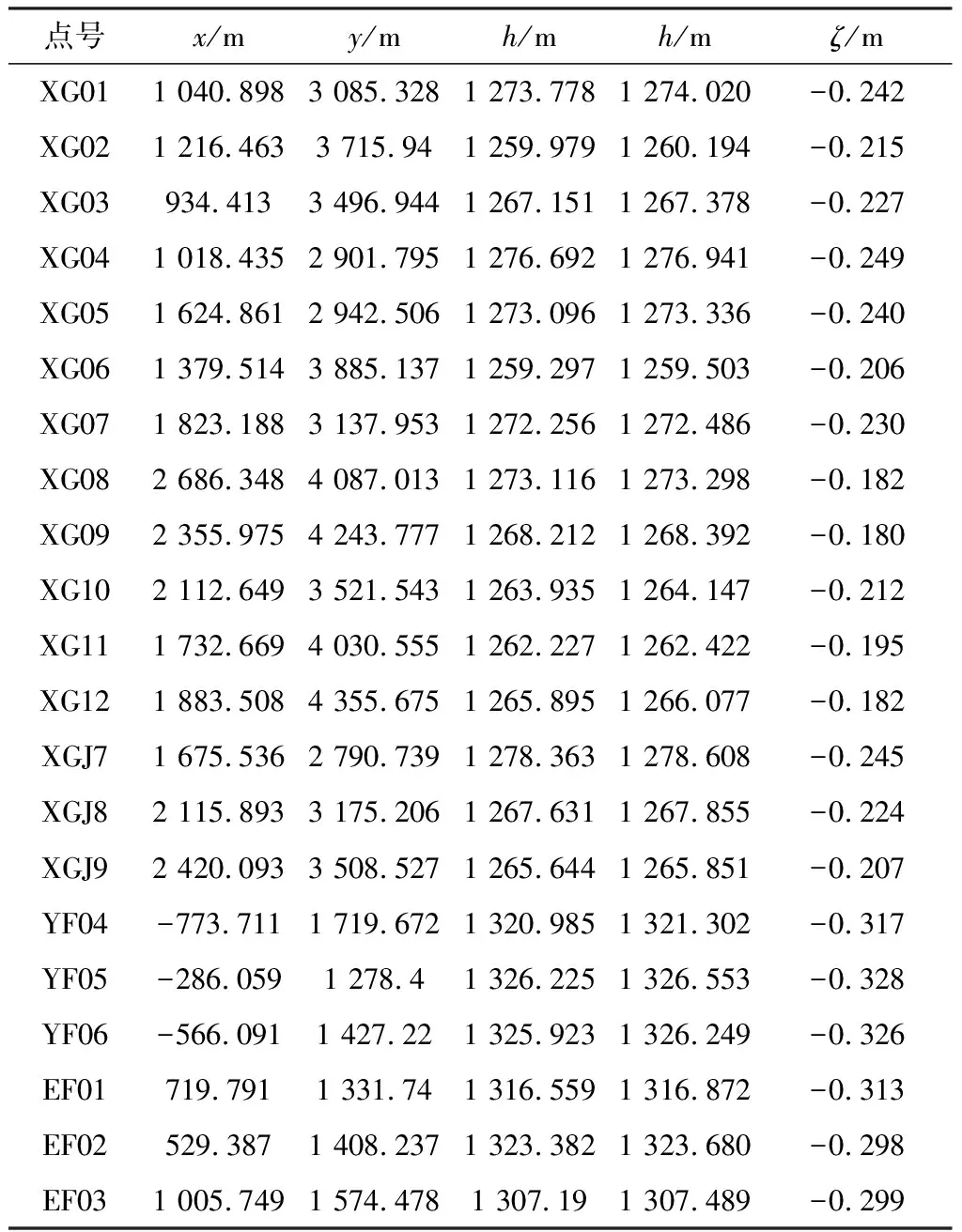
表1 GNSS/水准重合点成果表

2.3 基于MATLAB程序计算求取拟合系数

通过Matlab程序对数据进行计算，部分代码显示如下

format long g；

m=length(P(：，1))；

B=zeros(m，6)；

for i=1：m；

B(i，：)=[1，P(i，1)，P(i，2)，P(i，1)×P(i，1)，P(i，2)×P(i，2)，P(i，1)×P(i，2)]；

end

ss=P(：，3)；

cs=pinv(B′×B)×B′×ss。

将数据代入计算出二次多项式拟合模型系数为

a0=-0.000 000 233 687 411 332 634

a1= 0.000 104 563 005 212 421

a2=-0.000 261 039 683 129 869

a3= 0.000 000 004 476 835 742 444 78

a4=0.000 000 054 012 643 907 004 7

a5=-0.000 000 029 420 139 308 138 1

2.4 通过计算的模型系数进行精度评定

通过Matlab程序对数据计算精度，部分代码显示如下

m=length(P(：，1))；

fori=1：m；

v(i，：)=[cs(1)+cs(2)×P(i，1)+cs(3)×P(i，2)+cs(4)×P(i，1)×P(i，1)+cs(5)×P(i，2)×P(i，2)+cs(6)×P(i，1)×P(i，2)]；

end

v

利用Matlab程序进行计算，并分别给出计算结果。参与计算的点残差值见表2，未参与计算的点残差值见表3。

表2 参与计算点残差值表

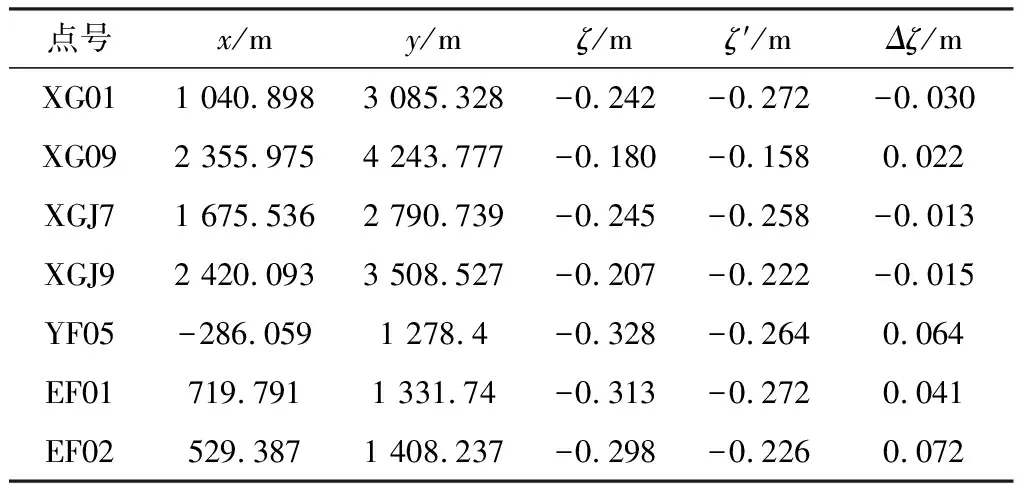
表3 未参与计算点残差值表

根据上述(6)式计算，内符合精度为σ内=0.030 m；上述(1～10)式计算，外符合精度为σ外=0.058 m。

3 结论

(1)各种GNSS/水准拟合法的精度都达到了厘米级的精度，选用合适的模型可以代替三、四等水准测量。

(2)在平缓地区GNSS/水准拟合法的精度大于起伏地区，所以地形对GNSS/水准拟合法精度的影响较大。

(3)选择不同拟合点数对精度的影响不是很大，通过比较并不是点数选择的越多其拟合精度就越好。