基于NAD算法的声波方程时间四阶差分解法

田雪丰

(中国煤炭地质总局地球物理勘探研究院，河北 涿州 072750)

数值模拟是研究复杂介质中地震波传播机理的重要工具[1-3]，高精度的正演模拟结果也可用于指导地震资料的采集方案设计和处理、反演流程设置[4-8]。基于高阶差分离散技术的有限差分算法[9-11]在以往的科学研究和工业生产中发挥了巨大作用。但随着业界对模拟精度要求的不断提高和地震勘探所面临的问题的复杂程度的不断增加，这种方法由于其固有缺陷的限制而越来越难以满足学术界和工业界的需求，其缺陷主要表现在：当波动方程差分阶数过小或地下介质中的地震波传播速度过低或地震波的频率过高时，常规有限差分算法往往会产生严重的数值频散问题，这种数值频散不是由介质本身的弹性性质引起的，而是由模拟算法本身引起的，其本质是一种误差，该误差会使地震波的振幅、频率和相位产生畸变，严重时还会产生虚假同相轴，因此带有数值频散的波动方程正演模拟结果是无法指导生产实践的，也无法用于地震波传播机理的分析，必须研究并采用适当的技术消除这种误差，确保模拟结果的精度。

目前，业界解决数值频散压制问题的主要思路有五：①减小时间和空间网格的剖分步长[12]；②提高波动方程导数项的差分离散阶数[13-15]；③优化偏导数项的差分系数[16-17]；④在数值频散产生之后采用适当算法对其进行压制[18-21]；⑤研究并采用新技术提高差分离散精度，减小频散误差[22-25]。

在常规速度模型和低频条件下，上述第一和第二种思路对数值频散的压制非常有效，实现起来也最为简单，但其缺陷也非常明显，表现为：空间剖分步长的减小意味着网格点的指数级增加，时间剖分步长的减小意味着成倍增加计算时间步数以获取相同记录长度的合成记录，两者会导致计算量和内存需求的指数级增大。提高波动方程导数项的差分离散阶数也会成倍增加计算量，并且当离散阶数增加到一定程度时，差分阶数的提高对于数值频散压制效果的提升会变得越来越缓慢。第三种思路一般不会增加计算量和内存需求，但对频散压制效果的提升有限。第四种思路以通量校正传输(FCT)技术[19-21]为代表，它基于先产生后压制的思路在波场延拓的过程中对波动方程的各个分量进行校正，当参数设置合理时，FCT技术具有明显的数值频散压制效果，但FCT技术的缺陷表现在：漫射通量和反漫射通量的求取以及反漫射通量的校正均需要消耗巨大的计算量，同时漫射因子和反漫射因子的设置没有明确的标准，难以合理设置，此外FCT技术在压制数值频散的同时还可能对有效信号造成损害，降低波场延拓的精度。

本文方法属于第五种思路，即在保持空间和时间网格大小、差分阶数等参数不变的前提下，依据数值频散的产生机理研究新方法来避免波场延拓过程中的数值频散，获取更高精度的模拟结果。具体为：利用NAD算子[23-28]求解各网格点处的高阶空间微分项，实现声波方程的差分离散，得到声波方程的水平梯度场和垂直梯度场，在此基础上推导基于NAD算子的时间四阶精度的差分格式，实现数值频散的压制。数值算例表明，本文基于NAD算子的时间四阶精度的波动方程差分格式对波场中的空间频散和时间频散均具有明显压制作用。

本文方法和第四种思路的区别在于：第四种思路本质上是先产生后压制，而本文方法是在事前避免其产生。本文方法和前四种思路的区别在于：前四种思路只能压制波动方程数值求解过程中产生的空间频散，不能压制时间频散，而本文算法可以实现这两种频散的同时压制。

1 基于NAD算子的声波方程时间四阶差分精度解法

1.1 差分格式推导

各向同性介质中的声波方程为：

(1)

其中，t为时间，x、y、z为直角坐标，v为纵波传播速度，u为质点位移。

在方程(1)中引入新变量U、W、P：

(2)

显然可得到以下关系式：

(3)

(4)

其中i、j、k、n分别为x、y、z三个空间方向和时间方向的离散点序号，Δt为时间剖分步长。

式(2)中，分别在n+1时刻和n-1时刻对U做泰勒展开得：

(5)

将式(5)中的两个方程求和并整理可得：

(6)

式(3)、式(4)、式(6)表明下一时刻的波场值和其梯度值可通过求解前一时刻波场的空间偏导数得到，因此声波方程的求解问题变成求解分量高阶空间偏导数问题。

将式(2)代入(6)式，可得：

(7)

(8)

(9)

(10)

(11)

将式(8—11)代入式(7)即可得到基于NAD算子的三维声波方程时间4阶精度差分格式。

经推导，式(7)的稳定性条件为：

(12)

其中vmax为计算空间中的最大地震波速度。

1.2 边界条件

边界条件是波动方程正演的重要内容，PML边界条件在许多波动方程正演中得到了成功应用[29-31]，本文也采用PML边界条件吸收入射到计算边界的外行波。图1为PML吸收边界条件的效果验证图，图中入射到边界的外行波被边界完全吸收，说明PML边界条件能够有效解决本文差分算法的边界伪反射问题。

2 数值频散分析

二维情况下可假设式(1)的平面谐波解为：

u(x,z,t)=u0exp(i(wt-kxx-kzz))

(13)

将上式代入式(7)中，整理可得式(7)的频散关系为：

(14)

式中，v为数值模拟得到的地震波传播速度，v0为模型速度，k为波数，w=kvΔt，φ=kΔx，φx=φcosθ，φz=φsinθ，θ为波的空间传播方向与x方向的夹角。

式(14)中以φ值为自变量，可以求得对应的w值，进而求得相速度和真实速度的比值为：

(15)

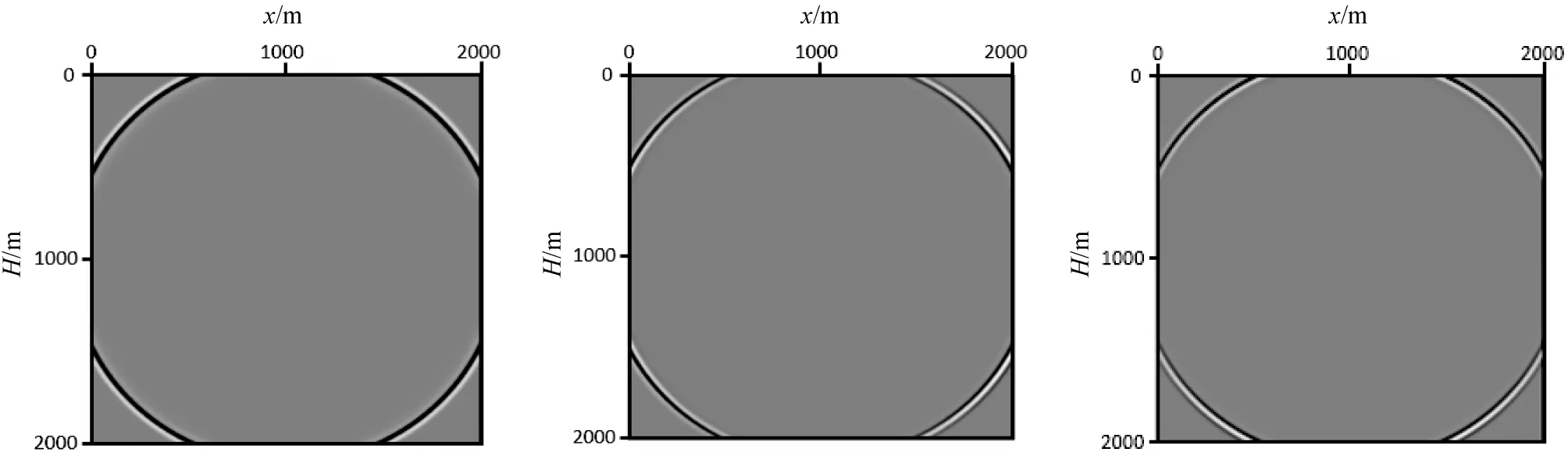
(a)u分量 (b)ux分量 (c)uz分量图1 截断边界效果验证图Figure 1 Truncated boundary effect verification

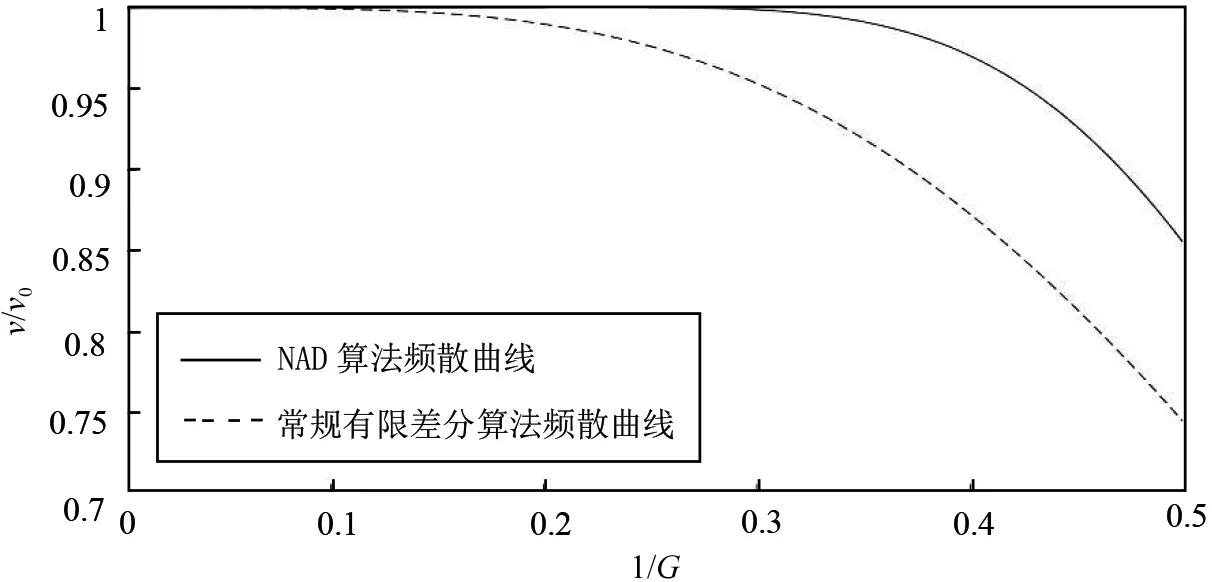
图2 NAD算法与常规差分算法频散曲线对比图Figure 2 Comparison of frequency dispersion curves from NAD algorithm and conventional difference algorithm

3 模型算例

3.1 均应介质模型

二维均匀介质模型的纵波速度为2 000m/s，模型大小2 000m×2 000m，按照10m×10m的空间网格大小差分离散该模型并进行正演模拟，模拟所用的震源为主频40Hz的Ricker子波，震源置于模型中央，时间采样间隔1ms。图3为采用常规有限差分法和本文算法正演得到的300ms时的波场快照，常规有限差分的波场快照(图3a)中存在严重的数值频散现象，这种频散的本质是一种算法误差而非介质本身的声学响应。利用这种含有误差的误差模拟结果进行波传播机理的分析会带来错误的分析结果，误导生产实践。同时，在一些基于波动方程求解的地震数据处理技术中，波场延拓过程中的数值频散还会在处理结果中产生虚假同相轴，降低处理精度。基于本文算法得到的波场快照没有数值频散，模拟精度更高(图3b)。

3.2 Marmousi模型

Marmousi模型如图4所示，分别采用常规有限差分法和本文算法进行正演模拟，模拟所用的参数为：震源为主频40Hz的Ricker子波，震源位于地表中间位置处，空间网格大小10m×10m，时间采样间隔1ms，全排列接收，接收点位于地表，道间距10m。图5为上述两种算法得到的t=1 400ms时的波场快照，图6为两种算法得到的合成地震记录，对比表明在上述时间和空间网格尺寸条件下，常规有限差分算法会产生严重的数值频散问题，模拟精度底，而本文算法得到的波场清晰干脆，没有数值频散。

(a)常规有限差分法的波场模拟快照 (b)基于NAD算法的波场模拟快照图3 常规有限差分法与基于NAD算法对均匀介质模型的波场快照Figure 3 Homogeneous medium model wave field snapshots from conventional finite difference method and NAD algorithm

图4 Marmousi速度模型图Figure 4 Marmousi velocity model

(a)常规有限差分法波场快照 (b)基于NAD算法波场快照图5 两种算法的波场快照对比Figure 5 Comparison of wave field snapshots from two algorithms

(a)常规有限差分法合成记录 (b)基于NAD算法合成记录图6 两种算法的合成记录对比Figure 6 Comparison of synthetic seismic records from two algorithms

4 结论

数值频散是有限差分求解波动方程时产生的一种误差，这种误差会使地震波的频带和波形发生畸变，还会产生虚假波场。常规有限差分算法中，当地震波频率较高或差分网格较大时，这种频散尤其严重。本文针对这一问题，推导了三维各向同性介质声波方程近似解析离散化数值模拟方法，相较于常规差分算法，本文算法在求解空间微分时同时利用了更多的点的波场信息，得到的空间微分更为准确，有效地压制了数值频散误差，得到了更高精度的波场快照和模拟结果。同时，由于本文算法在大网格尺寸条件下能得到无频散的波场模拟结果，因此相同模型条件下，可采用大网格对模拟空间进行差分离散，减少网格数，这在客观上降低了模拟所需的内存需求，也提高了计算效率。