地下水开采引发的土体变形对污染物迁移影响研究

马青山，贾军元，田福金，雷 廷

(中国地质调查局南京地质调查中心，南京 210016)

0 前言

地下水开采引发的地下水污染问题一直以来备受国内外许多学者的高度重视[1-3]。当前，地下水污染物迁移的研究多以刚性多孔介质中溶质运移的对流-弥散理论为主[4]，而忽略了多孔介质变形对污染物迁移产生的影响。事实上，在地下水开采过程中，地下水位下降，土体有效应力增加，土体压缩变形，含水层中孔隙水的渗流特征会发生变化，进而影响污染物随土体孔隙中水的运动。因此，研究变形介质中污染物迁移特征对保护地下水环境具有重要的现实意义。

在过去二十年中，多孔介质中污染物迁移的研究已经开始考虑土体的固结耦合效应。Loroy等人首先分析了溶质迁移过程中孔隙介质的固结效应，然而却没有正确反映多孔介质变形对对流-扩散方程中对流项的影响[5]。此后Smith等人通过对粘土固结进行应变分析，提出了饱和变形多孔介质的一维污染物运移理论[6]。Alshawabkeh等研究了黏土层体积变化对一维污染物溶质运移的影响，提出了同时考虑固结作用和溶质扩散的方程[7]。lewis等考虑了大变形情况下的污染物迁移情况，探讨了固结变形、对流、有效扩散系数等因素对污染物迁移的影响[8]。王水林等考虑了二维情况下孔隙介质变形对溶质运移的影响，提出了考虑孔隙介质固结效应的溶质运移方程，并给出了相应的求解方法[9]。张志宏等提出了黏土防渗层中污染物迁移转化的一维数学模型，并在合理简化的基础上给出了模型的解析解[10]。

但上述成果都限于局部尺度，主要研究荷载引起衬垫层变形对污染物迁移的影响。本文考虑了大尺度松散沉积层固结过程中污染物的迁移，以地下水渗流理论、太沙基一维固结理论和溶质运移对流-弥散理论为基础，同时考虑孔隙度、渗透系数、水动力弥散系数的动态变化，通过建立变形土体地下水污染物迁移三维耦合数值模型，研究了地下水开采引起的土体变形对污染物迁移造成的影响。

1 理论基础

1.1 地下水三维非稳定流

根据渗流连续性方程和达西定律，对于各向异性介质，以主渗透方向为坐标轴方向，则描述地下水运动的三维非稳定流方程可表示为[11]：

(1)

式中：Kxx、Kyy分别为水平渗透系数，m/d；Kzz为垂向渗透系数，m/d；h为t时刻点(x,y,z)的水头值m；W为即源汇项，1/d；μs为储水率，1/m；t为时间，d；Ω为计算域。

1.2 污染物迁移对流-弥散方程

地下水中污染物的迁移和转化是物理、化学及生物作用的一个综合过程[12]。在不考虑污染物吸附、化学反应以及生物降解的情况下，描述任意时刻多孔介质污染物迁移规律的水动力弥散方程可表示为(选取渗流主方向与坐标轴方向一致)[13]：

(2)

式中：c为流体中溶质的质量分数，mg/L；n为孔隙度；I为源汇项；Dxx、Dyy、Dzz为沿坐标轴方向的水动力弥散系数分量，m2/d；vx、vy、vz为介质中流体沿坐标轴方向的平均线性速度，m/d。

1.3 土体变形计算方法

针对地下水开采引起的土体固结变形问题，本文采用太沙基一维固结理论进行阐述。根据Terzaghi有效应力原理，假定土体总应力保持不变，并且认为土体只在垂向上发生变形，则土体一维变形计算方程如下[14]：

Δb=-Δhμskb0

(3)

式中：Δb为含水层的变形量，m；μsk为含水层土体的骨架储水率，1/m；Δh为水头变化值，m；b0为含水层的初始厚度，m。

根据含水层有效应力与前期固结应力的相关关系，将含水层变形分为弹性变形阶段和非弹性变形阶段，对应土体变形的不同阶段，土体骨架储水率的变化分别为[15]：

(4)

1.4 参数动态变化

1.4.1 孔隙度与渗透系数的非线性

地下水开采过程中，根据有效应力原理，随着地下水的不断开采，水位不断降低，孔隙水压力逐渐减小，含水层土体的有效应力逐渐增加，孔隙度逐渐减小，含水层渗透系数随之不断变化。这些变化又影响孔隙流体的流动和压力分布。因此，有必要考虑多孔介质中应力场与渗流场之间的相互作用。

假设土层厚度为b0，由于降水引起的沉降量为Δb，不考虑土层的侧向变形，则对于固结过程中孔隙度n有[15]：

(5)

一般地，沉降量与土层厚度相比非常小，因此，式(5)可简化为：

(6)

根据Kozeny-Carman方程，渗透系数的变化可用表示为：

(7)

1.4.2 水动力弥散系数的非线性

土体固结变形下的污染物迁移问题属于多场耦合问题，即应力场、渗流场和浓度场之间的耦合。当其中一个物理场发生变化时，必将会引起其他物理场变化。土体在压密过程中，孔隙度、渗透系数将发生变化，进而引起水动力弥散系数的改变。水动力弥散系数的动态表达式如下[16]：

(8)

式中：Dm为分子扩散系数，m2/d；Dxx、Dyy、Dzz为水动力弥散系数张量对角线元素；αL为纵向弥散度，m；αT为横向弥散度，m。

1.5 初始条件

地下水渗流初始条件为：

h(x,y,z,t)|t=0=h0(x,y,z)，(x,y,z)∈Ω

(9)

式中：h(x,y,z,t)为渗流场水头，m；h0(x,y,z)为初始水头值，m。

溶质运移初始条件为：

c(x,y,z,t)|t=0=c0(x,y,z)，(x,y,z)∈Ω(10)

式中：c(x,y,z,t)为浓度场质量分数，mg/L；c0(x,y,z)为初始质量分数值，mg/L。

地面沉降初始条件：

Δb(x,y,z,t)|t=0=0，(x,y,z)∈Ω

(11)

1.6 边界条件

地下水渗流边界条件包括：

h(x,y,z,t)|Γ1=h1(x,y,z,t)，t>0，(x,y,z)∈Γ1

(12)

(13)

(14)

式中：h1(x,y,z,t)表示边界Γ1上点(x,y,z)在时刻t的水头值，m；n为边界Γ2的外法线方向；q(x,y,z,t)为已知函数，表示单位面积上流入(流出)的量，m/d；cos(n,x)、cos(n,y)、cos(n,z)分别为流量边界外法线方向与坐标轴方向夹角的余弦；μ为给水度；z(x,y,t)为各计算节点标高，m；cosθ为自由面外法线方向与铅垂线之间的夹角。

污染物运移边界条件包括：

c(x,y,z,t)|Γ1=cb(x,y,z,t)，(x,y,z)∈Γ1

(15)

(16)

(x,y,z)∈Γ3

(17)

式中：Γ1表示定浓度边界；cb(x,y,z,t)为任意时刻渗流域内第一类边界(Γ1)上流体中已知污染物的浓度分布；q(x,y,z,t)表示Γ2边界上已知的弥散通量；cos(x,n)、cos(y,n)、cos(z,n)分别为边界Γ2外法线方向与坐标轴方向夹角余弦。若边界为不透水边界时，边界上没有物质交换，即边界上的弥散通量为零时，则q(x,y,z,t)=0。g(x,y,z,t)为已知函数，表示Γ3边界法线方向上的对流弥散总通量。

采用伽辽金有限元法对上述控制方程进行离散，结合初始条件，边界条件和参数的动态变化模型即可运用Fortran语言编制相应的有限元程序进行求解。

2 应用算例

2.1 研究区概况

研究区位于长江三角洲平原，沉积了巨厚的第四纪松散沉积物，地下水以第四系松散孔隙水为主。由于水文地质条件的不同加之成因历史的差异，“上咸下淡”的地下水水质格局普遍存于相邻含水层中，即水质较差的咸水贮存在浅部的含水层中，而水质较好的淡水则分布在下部较深的含水层中。根据水文地质条件，将研究区含水层细分为7层。垂向从上往下依次为：潜水含水层、第I承压含水层，第II承压含水层、第III承压含水层以及各含水层之间的粘性土弱含水层，其中潜水含水层岩性以粉砂为主，底板埋深20～30m，静水位埋深0.9～1.2m；第I承压含水层岩性以粉砂亚砂土为主，底板埋深62～70m，静水位埋深3.2～3.8m；第II承压含水层岩性亚砂土、细中砂为主，底板埋深93～110m，静水位埋深7.6～8.18m；第III承压含水层岩性以细中砂、中粗砂为主，底板埋深125～150m，静水位埋深11.5～13.4m。

2.2 模型离散

模型的平面尺度为1 000m×1 000m，垂向深度为150m。模型采用六面体八节点单元进行空间离散，平面上剖分为2 400个矩形网格单元，一共分成16 800个网格单元(图1)。垂向上从上往下依次剖分为：潜水含水层、第I、第II、第III承压含水层及其之间的粘性土弱透水层共7层。各层均概化为均质各向异性，并且均按独立的层位参与计算，另外各层之间均发生水力联系，地下水流态为三维非稳定流。潜水含水层、第I、第II、第III承压含水层底板标高分别为-25、-67、-107、150m。每层划分为一个参数分区，共划分为7个参数分区。模型四周概化为第一类边界条件-已知水头和已知浓度边界，顶部为自由面边界。底部与下覆承压含水层之间有较厚的粘土层，将其概化为隔水边界和零通量边界。

图1 模型剖分示意Figure 1 A schematic diagram of model subdivision

2.3 地下水开采条件下污染物运移模拟研究

模型选择氯离子为模拟因子，潜水含水层、第I、第II、第III承压含水层的初始水位分别为-1、-3.5、-7.8、-12.2m，初始氯离子的质量分数分别为2 485、1 775 、1 065 和35.5 mg/L。模型模拟时间为30d。每天为一个时间步长，共30个时间步长。抽水井位于X=500m，Y=500m处，抽取第III承压含水层地下水，抽水量为500m3/d。观测点位于距离抽水井5m处的第III承压含水层。

模型各参数分区参数值如表1所示。假设模型中各参数分区的纵向弥散度相同，值为10m，且弥散度的纵横比采用常用的经验值，即横向弥散度与纵向弥散度的比值均为0.1。

表1 模型参数

3 结果分析

3.1 参数动态变化特征

参数准确性对模型计算结果的精度有着深刻的影响。考虑土体变形效应，污染物迁移问题实际上是应力场、渗流场和浓度场之间相互影响、相互作用的多场耦合问题。地下水开采引发土体变形、土体水力学参数和土力学参数以及水动力弥散系数均会发生变化。因此，有必要正确模拟参数的变化过程。选取观测点(495，495，-130)所在的单元进行孔隙度、渗透系数和水动力弥散系数的变化分析。

图2 孔隙度沿抽水井径向方向变化趋势Figure 2 Variation trend of porosity along pumping well radial

图3 孔隙度和地下水位动态变化趋势Figure 3 Dynamic variation trends of porosity and groundwater level

不同时刻孔隙度随抽水井径向距离的变化趋势如图2所示。从图中可以看出，孔隙度的最大变化发生在抽水井附近，孔隙度减少至0.399 3。

图3反映了抽水期间孔隙度和地下水位随时间的变化趋势。从图中可以看出，孔隙度和地下水位的变化趋势一致。地下水开采、地下水位降低、土体有效应力增大，导致土体压缩变形，从而引起孔隙度的变化。地下水位达到稳定，孔隙度不再发生改变，此时地下水位下降11m，孔隙度从0.4减小至0.399 6。

图4 渗透系数沿抽水井径向方向变化趋势Figure 4 Variation trend of permeability coefficient along pumping well radiation

图5 渗透系数和地下水位动态变化趋势Figure 5 Dynamic variation trends of permeability and groundwater level

图4反映了水平渗透系数在不同时刻随抽水井径向距离的变化趋势。从图中可以看出，在井附近，水平渗透系数的值在1天内下降至0.993m/d。

渗透系数随地下水位的变化关系如图5所示。可以看出，渗透系数和地下水位变化趋势一致，地下水位下降时，土体被压密，孔隙度减小，土体出水能力变弱，从而导致渗透系数减小。第15d时，地下水位达到稳定，渗透系数从1m/d减小至0.995 7m/d。

水动力弥散系数和地下水位之间的关系如图6所示。图中水动力弥散系数与地下水的变化呈现相反的趋势，开采地下水时，水位下降较快，水力梯度较大，渗流速度较快，对流作用明显，因此，水动力弥散系数变大。当地下水位达到稳定时，渗流场和应力场状态不再发生变化，孔隙度、渗透系数和渗流速度也不再变化，因此水动力弥散系数也随之达到稳定状态。

图6 水动力弥散系数和地下水位动态变化趋势Figure 6 Dynamic variation trends of hydrodynamic dispersion coefficient and groundwater level

3.2 污染物迁移规律研究

图7～图8反映了考虑土体固结效应和未考虑土体固结效应两种条件下，水平水动力弥散系数和垂向水动力弥散系数随时间的变化趋势图。从图中可以看出，土体固结效应条件下，水平水动力弥散系数和垂向水动力弥散系数的值均小于未考虑土体固结效应下的值。这是因为土体固结变形、孔隙度和渗透系数减小，地下水平均线性速度减小，进而导致水动力弥散系数的减小。

图7 考虑土体固结和未考虑土体固结条件下水平方向水动力弥散系数对比Figure 7 Contrast of horizontal hydrodynamic dispersion coefficients both considered and not considered soil mass consolidation

图8 考虑土体固结和未考虑土体固结条件下垂向方向水动力弥散系数对比Figure 8 Contrast of vertical hydrodynamic dispersion coefficients both considered and not considered soil mass consolidation

图9反应了考虑土体固结效应和未考虑土体固结效应两种情况下观测点处Cl-的质量分数变化趋势，从图中可以看出：考虑土体固结效应条件下Cl-的质量分数变化曲线较未考虑土体固结效应的曲线平缓，浓度值比未考虑土体固结效应模拟时的偏小，到模拟最后时刻第30天，考虑土体固结效应观测质量分数为401.5mg/L，小于未考虑土体固结效应时的418.3mg/L。其原因主要是地下水开采，土体有效应力增大，土体骨架压缩变形，地下水平均线性速度减小，导致水动力弥散系数增幅减小(图7～图8)，进而延缓了溶质运移的过程。由此可见，土体压缩变形对污染物传输起抑制作用。

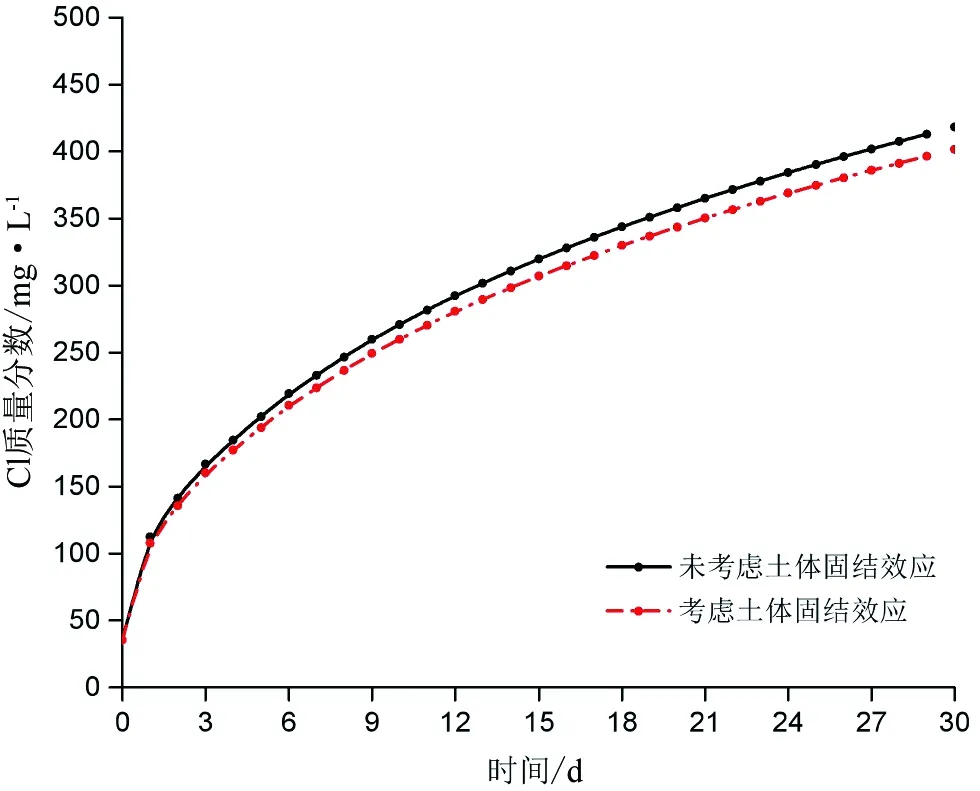
图9 第III承压含水层观测点处氯离子变化趋势Figure 9 Variation trends of chloridions on confined aquifer III observation points

4 结论

地下水开采过程中引发的土体变形对污染物迁移的影响研究是地下水环境保护工作中面临的一个新的重要难题，通过本次模拟研究可以得出如下结论：

1)基于地下水渗流理论、太沙基一维固结理论和溶质运移理论，同时考虑孔隙度、渗透系数、水动力弥散参数的非线性变化，建立了变形土体污染物运移三维耦合数值模型。在此基础上，通过对实际案例的模拟分析，研究了土体固结变形与污染物迁移三维耦合作用下污染物迁移的规律，模拟计算了污染物浓度的变化趋势，计算结果更加科学真实。

2)通过对实际案例模拟分析可知，地下水开采，土体中的孔隙水压力减小，土体有效应力增大，土体发生固结变形，孔隙度减小，导致渗流速度减慢，从而减缓了污染物的对流扩散机制，也就是说，土体固结作用对污染物在多孔介质中的运移起抑制作用。