90°弯管内高黏原油水环流动特性的数值研究

1. 中国石油大学(华东)储运与建筑工程学院, 山东 青岛 266580;2. 中国石油管道局工程有限公司, 河北 廊坊 065000;3. 长庆油田分公司第三采油厂, 宁夏 银川 750011

0 前言

随着轻质石油的不断开采,油田已经进入稠油开采阶段。而使用稠油输送最主要的问题在于其黏度过高。稠油常用输送方法为加热、稀释和乳化等方法,但存在能耗高、建设成本高、油品品质变化大等问题[1]。因此,水环输送作为一种相对节能的方法应运而生。

Dove I J等人[2]在其专利中首次提出，在输送高黏液体时可以用水来润滑管道壁面来减小摩擦。屠大燕等人[3]通过理论与实验,探究了水环同心输送过程中的流动参数特性,建立了水环输送高黏油的效率与摩阻之间的关系式。敬加强等人[4]进行了稠油流动边界层水基泡沫减阻模拟，发现边界层中的泡沫可以隔离水平管道中上部的油壁界面,而液膜可以润滑水平管道下部的油壁界面,不仅解决了水环输送稠油时的偏心问题,而且可以减少水环输送稠油时的耗水量。贺成才[5]针对宾汉流体偏心环状管流进行了数值模拟,通过计算得到了对工程应用有重要价值的流动规律。Bannwart A C[6]对水环流动的建模方面进行了研究，发现核心环状流要求两种液体互不相混,且要求两种液体黏度不同,密度相差很小,且界面张力在环形结构中起重要作用。Ghosh S等人[7]使用FLUENT模拟了180°弯管中润滑油和水的核心环状流，在给定的条件下,与水平和向下流相比,U形弯管的核心在向上流动中污染壁面较小。郭旭等人[8]运用CFD软件,分别对水环通过45°和90°弯管工况下的流场进行了模拟，分析确定采用水环输送技术时爬升相同的高度下应选择90°弯管来提高管线高程。JingFan等人[9]模拟油水两相流通过Π型管道,结果揭示了油水两相流的界面结构、两种流体分布、压力和速度分布信息，为优化操作和几何参数提供了参考依据。Park S M等人[10]采用VOF模型对90°弯管核心流和90°弯管单相流进行了比较，同时模拟了弯管中有无界面张力对核心流的影响。Ooms G等人[11]模拟了90°弯管中的偏心环状流,由于核心与环形界面处法向力达到平衡,偏心环状流在90°弯管中可能存在的。

一般而言,前人对水环的研究大多集中在水平直管或者立管上,而输送稠油过程中不可避免地会经过弯管部件,前人对水环通过弯管时的研究却较少。与直管内的水环流动相比,弯管中的流动更加复杂。由于离心力对弯管中流型的影响,很可能导致水环通过弯管时油品偏心污染管壁。因此系统地研究水环通过弯管的稳定性具有实际意义。本文通过FLUENT软件，详细分析了90°弯管中不同界面张力对水环结构的影响，为水环通过弯管提供了理论参考依据。

1 模型的建立

由于要考虑离心力的影响,为了充分反映弯管内部流场的流动情况,研究采用三维模型，弯管结构见图1。本文选择坐标系为笛卡尔坐标系,x轴为轴向,y、z轴为径向，入口采用直流入射形式,油入口管道直径7.44 mm,水入口为环形入口,管道直径9.52 mm,其中管道的曲率半径28.56 mm,曲率比1/6,直管长度20 mm[12]。

模拟使用FLUENT软件求解器,采用瞬态模拟条件。模拟基于两种流体互不相溶的假设,液体性质恒定且液体通过直喷嘴同轴进入管道。

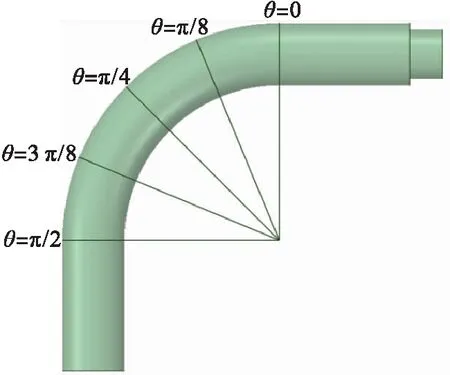
图1 弯管结构

1.1 控制方程

常见的两相流计算模型有：VOF模型、Eulerian模型、Mixture模型[13]。由于高黏油和水是互不相溶的两种液体,并且两相界面的位置是判定水环稳定性的关键参数之一,因此选用VOF模型用于数值计算。

连续性方程如下:

(1)

式中:ρ为流体密度,kg/m3;U为速度,m/s;t为时间,s。

在VOF模型算法中,FLUENT软件对于整个流场区域只求解一个动量方程,见式(2)。该动量方程的求解结果取决于每相流体的体积分数所决定的密度和黏度等参数。

+(ρg)+F

(2)

式中:P为流场中的压力,Pa;g为重力加速度,m/s2;F为作用于系统的力,kg/m2s;μ为流体黏度,Pa·s。

式(2)使用的密度和黏度可用式(3)～(4)表示:

(3)

(4)

式中:p为相数,本文中p=2;αq为第q相的体积分数;ρq为第q相的密度,kg/m3;μq为第q相的黏度,Pa·s。

1.2 湍流模型

由于水与油物性稳定、互不相溶，水环稳定后存在明显的界面,选择VOF模型与标准k-ε模型进行水环模拟[14-16]。标准k-ε模型是一个半经验公式,具有适用范围广、精度高、经济性好等优点,广泛应用于复杂流场模拟。

标准k-ε模型的基本运输方程为:

(5)

(6)

(7)

(8)

式中:kt为湍流动能,m2/s3；εt为耗散速率,m2/s3；μt为涡流黏度,Pa·s；Cμ=0.09；σk=1；σε=1.3；C1ε=1.44；C2ε=1.92;Ui、Uj分别为速度在i和j方向的分量，m/s;Xi、Xj为位移在i、j上的分量，m;Eij为主流时均应变率。

1.3 边界条件

弯管水入口和油入口采用速度入口，主管道末端出口设为压力出口，弯管所有壁面均采用无滑移边界条件，保持入口速度0.3 m/s,出口压力0.1 MPa。

1.4 物性参数

初始模拟中油黏度0.2 Pa·s,水黏度0.001 Pa·s;油密度900 kg/m3,水密度1 000 kg/m3;水相表面张力0.3 N/m[17]。

1.5 模型验证

采用Ghosh S等人[7]的模型和实验结果进行数值方法的验证。研究管段的油相进口直径8 mm,长度50 mm；观测管段直径12 mm,长度480 mm。根据实验参数建立模型,见图2。

Ghosh S等人的实验与模拟所采用的条件与本文一致。实验和模拟中测量了不同流速情况下,水环沿轴向方向的单位压降。采用本文所述数值计算方法进行模拟,模拟与实验的稠油体积分数对比见图3,实验结果与模拟结果对比见图4。

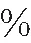
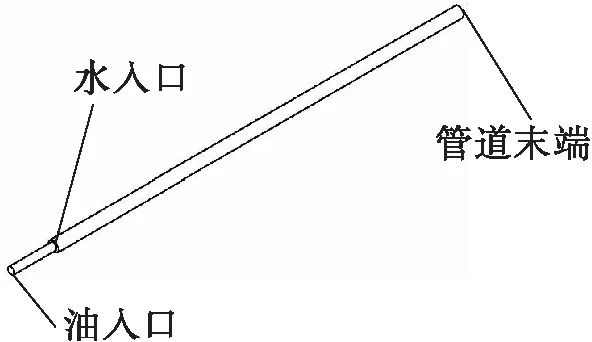
图2 管道结构模型

图3 稠油体积分数云图

图4 模拟结果与实验数据对比

2 数值模拟

2.1 计算域网格的划分

计算域网格的划分采用ICEM软件。由于研究的弯管结构比较复杂,因此网格采用三维非结构化网格的划分方法。弯管模型网格划分[18-20]见图5。

图5 弯管模型网格划分

2.2 网格独立性验证

对不同数目下的网格进行了独立性检验,网格数目分别为321 943、3 461 662、4 527 931。三种网格的油水分布曲线见图6,可看出油水分布曲线基本不变,满足网格无关性要求,为使模拟时油水界面更加清晰,本模型网格单元划分总数最终选择3 461 662。

图6 模拟结果对比三种网格的油水分布曲线

3 结果与讨论

当水环通过弯管时,由于受到离心力的作用,水环会逐渐向弯管外侧偏移,甚至会逐渐失稳,影响减阻效果。因此研究水环在弯管中的稳定性具有实际意义。

稠油体积分数在弯管中的分布见图7，从图7可看出,当θ=0时,核心油流在进入弯管前被水层包裹着沿核心向前流动，油相体积分数以中心轴为对称中心呈轴对称方式分布；当θ=π/8增加到θ=π/2时,核心油流逐渐向管壁一侧偏移,并随弯管的角度增大核心偏移越明显。当θ=0时,在半径比-0.65～0.65区域,油相体积分数保持为1,核心油流主要集中在管道中心；当θ=π/4时,在半径比 -0.7～0.4区域,油相体积分数保持为1,核心油流已经向管道外侧偏移；当θ=π/2时,在半径比-0.75～0.35区域,油相体积分数保持为1,核心油流此时严重偏心。水环流过弯管后,核心油流保持偏移向一侧管壁的形状向前流动。因此,弯管促使水环失稳。

图7 稠油体积分数在弯管中的分布

3.1 表面张力对弯管水环的影响

当水环在水平直管段流动时,由于油水之间存在密度差,核心油流受到上部水层作用的浮力逐渐向管壁上侧移动。水环失去稳定性,减阻效果大大降低。而在水中加入少量高分子聚合物,将水环变成黏弹性水环,增大了水环的界面张力,不仅可以进一步降低水环的摩阻损失,其黏弹效应还能克服核心油流的偏心趋势,增大水环的稳定[6]。当核心油流在浮力的作用下向管壁上侧靠拢时,由黏弹性水层所产生的第二法向应力差会产生方向朝下的平衡力,而且核心油流偏心越严重,这个力越大,而作用在核心油流上的上浮力却不变,随着核心油流上浮,平衡力越来越大直到两者相等,此时核心油流处于平衡位置[21]。

图8为不同界面张力下水环在管道中的油水体积分数切向分布图,图9为不同界面张力下油芯在管道中的位置。当θ=0时,不同界面张力下,在半径比-0.65～0.65区域,核心油相体积分数保持为1;当θ=π/4,界面张力0.15 N/m时,半径比-0.7～0.6区域,核心油相体积分数保持为1,界面张力增大至0.25 N/m 时,核心油相体积分数为1的半径比区域为-0.65～0.65;当θ=π/2,界面张力0.15 N/m时,在半径比-0.75～0.35区域,核心油相体积分数保持为1,界面张力增大至 0.25 N/m 时,核心油相体积分数为1的半径比区域为-0.65～0.65。从图8～9中可以看出，当界面张力 0.15 N/m 时,弯管内部核心油流靠近管壁,经过弯管后核心油流偏移严重,当界面张力增大到0.25 N/m时,弯管内部核心油流仍保持在管道中心,经过弯管后核心油流仍保持不变。

图8 油水体积分数切向分布

图9 油芯在管道中的位置

3.2 界面油水体积分数分布

图10为界面张力0.15 N/m时弯管截面的油相体积分数分布曲线,由图10可以看出，当θ=0时,半径比-0.65～0.65的区域，稠油体积分数保持为1,表明在经过弯管之前,核心油流聚集在管道中心,被水层包裹着向前流动,油相体积分数以中心轴为对称中心呈轴对称方式分布,而随着弯管角度的增大水环逐渐向管壁一侧偏移,水环流过弯管之后,核心油流保持向一侧管壁偏移的形状向前流动。随着界面张力的增大,核心油流在弯管中的偏移情况逐渐减弱。从图9可知,当界面张力为0.25 N/m,在经过弯管时,随着弯管角度的增大向管壁一侧偏移的趋势很小,水环经过弯管之后,核心油流仍聚集在管道中心,被水层包裹。

图10 水环在弯管各中截面的油相体积分数分布曲线

3.3 界面速度分布

图11为界面张力为0.15 N/m时弯管不同截面的轴向速度分布。由图11可看出,模拟条件下稠油体积分数分布随弯管角度的变化而变化。当θ=0时,半径比-0.65～0.6区域,中心油速保持在0.375m/s左右;半径比0.6～1.0区域,中心油速骤降为0 m/s。说明管道核心处被稠油所占据,且中心油速基本保持不变,而环形水层区速度梯度很大,剪切最强烈的地方发生在水层区,即弯管中水环的存在大大降低稠油输送摩阻。半径比-1.0～-0.65区域,中心油速由0 m/s急剧增加到0.375 m/s,速度梯度较半径比0.6～1.0区域更大,剪切最强烈,且剪切厚度变小。说明弯管外侧的水环在离心力的作用下受到核心油流挤压而变形,水膜厚度变小。同时,随着弯管偏转角度的增大,弯管外侧速度梯度增大,剪切区域逐渐变小;内侧速度梯度减小,剪切区域变大。这说明,随着弯管角度增大外侧水层厚度逐渐变小,弯管外侧水层受到的离心力增大,造成受到核心油流挤压作用增大,最终导致水环通过弯管偏心并逐渐失稳。

图11 水环在弯管不同截面处的轴向速度分布

3.4 界面压力分布

图12为界面张力0.15 N/m时弯管不同截面处的压力分布。由图12可看出,弯管压力分布呈现弯管外侧压力高、内侧压力低且油芯压力高于外侧水环压力的情况。并且随着弯管偏转角度的增加,弯管中压力较高的核心油流部分向管壁外侧偏移。

图12 水环在弯管不同截面处的压力分布

4 结论

本文借助FLUENT软件研究了不同工况下水环在90°弯管中的流动情况。得出结论:增大界面张力可以显著地增加水环通过弯管时的稳定性,在不同界面张力下当界面张力为0.15 N/m时,由于核心油流所受向上的浮力大于第二法向应力差产生的向下平衡力,水环偏心严重,逐渐失去稳定性;当界面张力为0.25 N/m时,水环经过弯管之后,核心油流所受的浮力与平衡力基本一致,核心油流仍聚集在管道中心,水环的稳定性最好。因此在实际输送过程中,当使用水环输送高黏原油时,可以通过增加适量的高分子聚合物来增加界面张力,从而增加水环的稳定性。