基于最小费用最大流改进算法的多种交通方式开行方案协同优化研究

赵璐阳，王丽娟，宋金凤

（1．石家庄铁道大学 交通运输学院，河北 石家庄 050043；2．河北东方学院 交通学院，河北 廊坊065001)

0 引言

城际铁路具有快速、便捷、舒适、环保等特点，《中长期铁路网规划》中明确提出要发展城际铁路以补充现代高速铁路网。城际铁路在城际间客运市场内与原有的既有铁路和公路运输存在竞争，同时因其票价较高、定线定员开行、路网规模有限等特点，又与既有铁路和公路运输存在协同优化的可能。因此，加强城际铁路、既有铁路和公路的协同合作，可以更好地服务于城市间客运市场。

目前国内对列车开行方案优化的研究较多，如从坐席分配、列车运行图、开行时段[1-3]等角度入手，通过对基于Logit[4]等模型构建的客流分配模型的求解，采用“按流开车”原则对铁路列车开行方案进行优化。除从微观角度针对某种交通方式的开行方案进行优化研究外，还有学者从宏观角度对多种交通方式间协同优化进行了研究。李国文等[5]研究了客运通道内多种交通方式间客流分配的协同优化问题；胡辉等[6]利用Benders分解技术对多方式物流运输网络优化模型的求解进行研究。求解交通相关问题时，图论理论被部分学者应用，Gutiérrez-Jarpa等[7]通过最小费用最大流算法为公路配送及轨道交通选线提供了优化思路；张天伟等[8]利用最短路求解思路优化了城际铁路设站时的城市选择方法。目前协同优化方法多样，图论相关理论虽然被广泛应用于求解各类交通问题，但利用最小费用最大流理论对多种交通方式开行方案进行协同优化的研究还相对较少。为此，在现有研究基础上，关注非拥挤状态下城际间运输通道内多种交通方式的旅客运输问题，并设计最小费用最大流的改进算法，对多种交通方式开行方案进行协同优化。

1 问题描述

1.1 假设条件

城际间交通系统大部分时期处于运能充足的状态即客流非拥挤状态的情况，通过对多种交通方式开行方案的协同优化研究，可以减少运能浪费并降低广义运输总成本，引导旅客合理选择出行方式并引导多种交通方式有序竞争。因此，非拥挤状态下城际间运输通道内多种交通方式的开行方案协同优化，主要考虑如何满足城际综合运输系统内大城市与中小城市间的旅客运输需求，包括旅客的换乘可能。城际间运输通道多种交通方式客运路网如图1中所示。

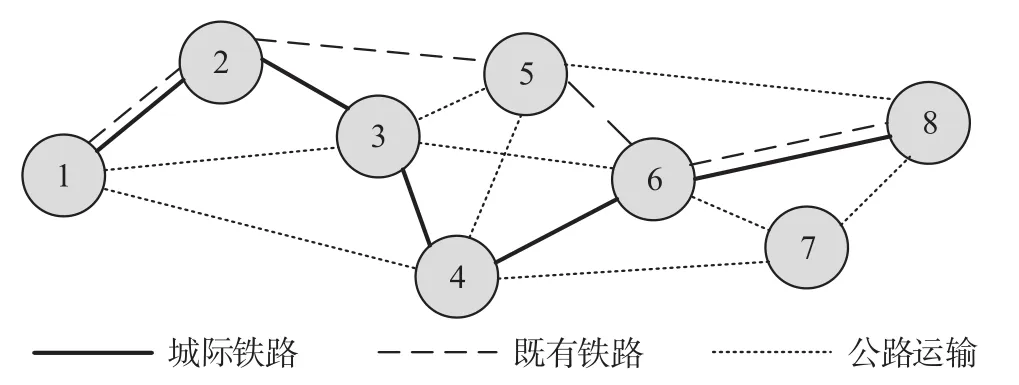
图1 城际间运输通道多种交通方式客运路网Fig.1 Multiple transport modes network in intercity transport corridors

城际间运输通道内多种交通方式开行方案协同优化研究，假设相邻城市间至少存在1种即公路运输的客运直达交通方式，而城际铁路及既有铁路只在大城市设枢纽站可始发或终到列车，2个大城市间的中小城市所设车站均为中间站，仅可停靠列车。

1.2 参数及变量定义

大城市1与大城市N分别为城际列车的起点和终点，依次对沿线中小城市进行1，2，…，N的自然序列编号。对城际间K种常用交通方式进行编号，规定K= 1表示城际铁路，K= 2表示既有铁路，K= 3表示公路运输。其余参数及变量分为以下4类。

（1）成本类参数。为城市i到相邻城市j之间第K种直达交通方式的广义运输成本(i，j= 1，2，…，N，K= 1，2，3)，元/人，取值范围≥0或= -1。认为当i=j时= 0；当城市i与相邻城市j间不存在K种直达交通方式时，或当城市i与城市j不是可直达的相邻城市时= -1 (K= 1，2，3)。C K为开行一列列车的广义运输成本(K= 1，2)，元/列，取值范围C K> 0。

（2）0-1变量。为判断是否为最低广义运输成本的0-1变量，当第K种直达交通方式是城市i到相邻城市j之间最低广义运输成本时，为1，否则为0。此时= 1的集合形成了城际运输通道内最低成本路网。Txy为城市x与城市y间相邻OD路段最低广义运输成本的集合，即Txy= {= 1 |=1，…，= 1}，为首尾相连的相邻OD路段的0-1变量集合，其中x与c，以及d与y分别为相邻城市。

（3）客流量类参数。axy为城市x至城市y的OD客流量，人，取值范围axy≥0。Aij为城市i到相邻城市j间路段客流承担量，人，取值范围Aij≥ 0。

（4）其他参数及变量。V K为K种交通方式的单位载客量即每趟列车或客车的载客量，人/列或人/辆，取值范围V K> 0。L K为城际铁路与既有铁路的合理开行数(K= 1，2)，列。其中合理开行数包括基础开行数和可调开行数2个部分。为城市i与相邻城市j间公路运输的合理开行数，辆，取值范围LK≥0，且为整数。

1.3 协同优化

为方便计算，需简化实际运输网络。首先，判断各城市间是否存在直达交通方式，即2个城市是否相邻；其次，比较各相邻城市间广义运输成本，确定成本最低的交通方式，逐一为0-1变量赋值，从而得到城际运输通道内最低广义运输成本客运路网，形成实际问题的赋权有向简单图。城际运输通道内最低广义运输成本客运路网示意图如图2所示。

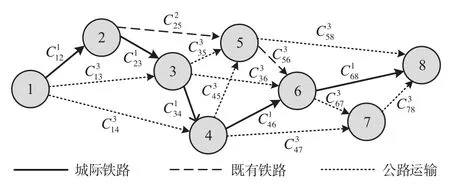
图2 城际运输通道内最低广义运输成本客运路网示意图Fig.2 Lowest social generalized transport cost passenger transport network

（1）成本参数逻辑关系。根据已知各相邻城市间多种交通方式的广义运输成本可得出城际铁路或既有铁路单向开行一列列车的广义运输成本，即

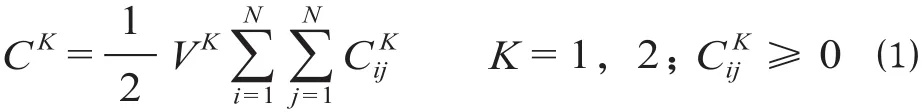
式中，认为相邻城市间上行和下行列车开行时广义运输成本相等，故列车单向开行时的广义运输成本等于往返开行时的一半。

（2）客流参数逻辑关系。根据已知OD客流量及计算出的OD间成本最小路径，对客流进行0-1分配，从而得到各相邻OD路段的初始客流承担量Aij，此时计算出的各OD间客流承担量应满足

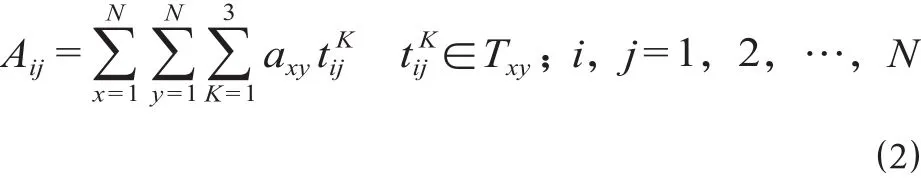
式中，如果Txy的集合中不存在= 1的成员，则取= 0。当某OD间并非成本最小路径或并非相邻OD路段时认为其不承担客流，即Aij= 0。在计算时，Aij的数值可能会被调整，调整后的客流承担量仍记为Aij。

（3）目标函数。所构建优化模型的目标函数为广义运输总成本最低，即

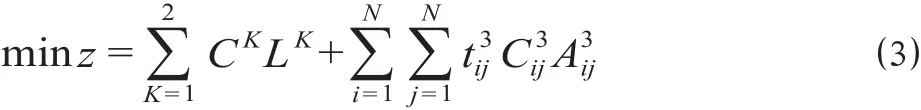
（4）0-1变量约束。求解最短路时为避免重复选线，已确定的0-1变量应满足

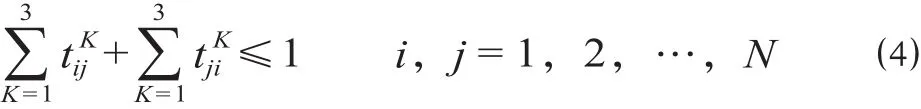
（5）客流约束。去往某城市的客流量及该城市发出的客流量应满足以下关系

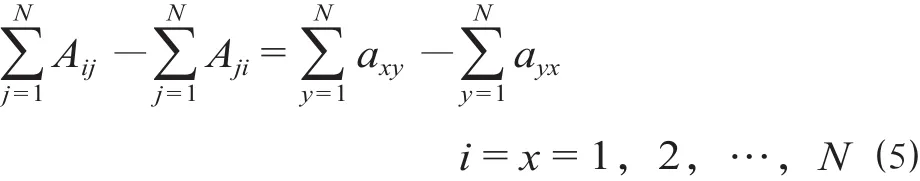
即从城市i发出路段的总客流承担量与进入城市i路段的总客流承担量之差，应等于客流OD表中在城市i下车的总客流量与在城市i上车的总客流量之差。

（6）开行约束。为保证协同优化的开行方案可提高运能的利用率，故开行方案应满足

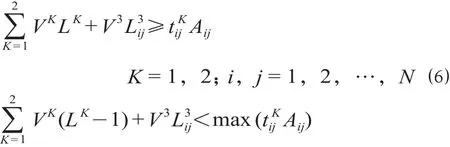
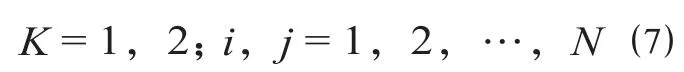
根据假设条件，在非拥挤状态下城际间运输通道内多种交通方式的开行方案协同优化运能充足，可满足客流需求，即如公式 ⑹ 所示。公式 ⑺ 目的是为确保运能的高效利用，避免开行过多列车。

由于公路运输时每辆车载客量较少，在协同优化开行方案时认为其合理开行数量应与客运需求相匹配，即公路运输提供的运能刚好满足公路运输需求。即

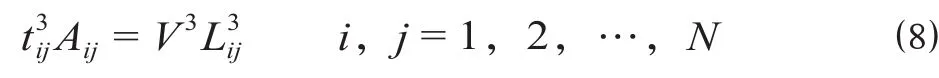
由于此类问题使用数学模型求解较复杂，当与实际网络相结合，利用网络的某些性质求解将有效提高其计算效率，因而将此类问题归纳为图论中最小费用最大流问题，并设计相关改进算法进行求解。

2 多种交通方式开行方案协同优化模型改进算法

对传统的最小费用最大流理论进行改进，认为其弧容量为各路段客流承担量而非路段通过能力，弧费用为各路段广义运输成本。在计算时对最小费用最大流常用算法之一的最小费用路算法进行了改进。首先，认为弧容量为弧流量的下限而非上限，计算结束时各弧流量需大于等于其容量但不宜过大；其次，认为弧容量是动态可变的，允许客流承担量即弧容量在路段间进行合理调整；最后，当弧流量大于等于弧容量时表示该弧已被满足，不能再作为增广链的一部分。改进算法分为3个部分，第1部分仅考虑铁路运输并依据传统算法求解出基础开行数；第2部分考虑3种交通方式并依据上述要求，通过寻找最小费用增广链调整系统流量，迭代至所有弧容量被满足；第3部分比较得出总费用最低的开行方案，确定可调开行数。

2.1 基础数据计算

根据运筹学图论中的最短路理论，使用Dijkstra算法求出每一对OD点间已知的广义运输成本的最短路，并将结果记录在最短路集合表中。最短路集合表样式如表1所示。在表1的基础上利用0-1分配法将已知OD交通客流量表中所有客流分配至其对应的最短路上，分配时需确保客流的连续，从而可快捷准确得出路段客流承担量表。路段客流承担量表样式如表2所示。

在计算最短路时可能出现成本相等的线路，称其为“可相互替换线路”，2条线路分别被括起或用斜体表示。按照“括起初始计算线路，斜体表示可替换线路”的原则进行标注，此2条线路不同时参与计算。

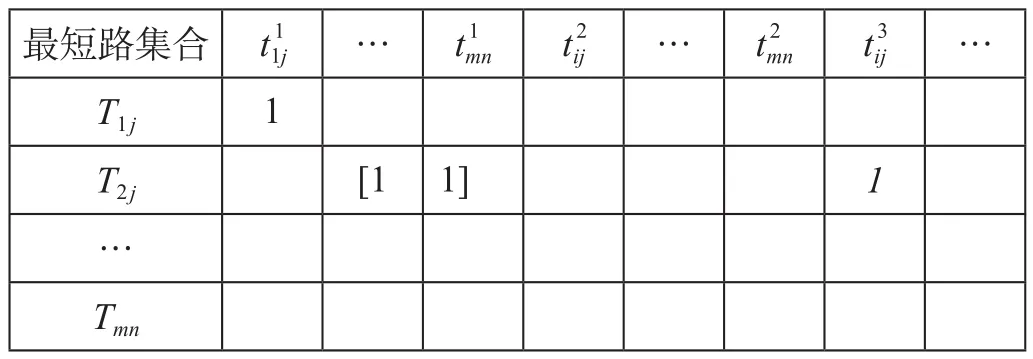
表1 最短路集合表样式Tab.1 Shortest path set table style

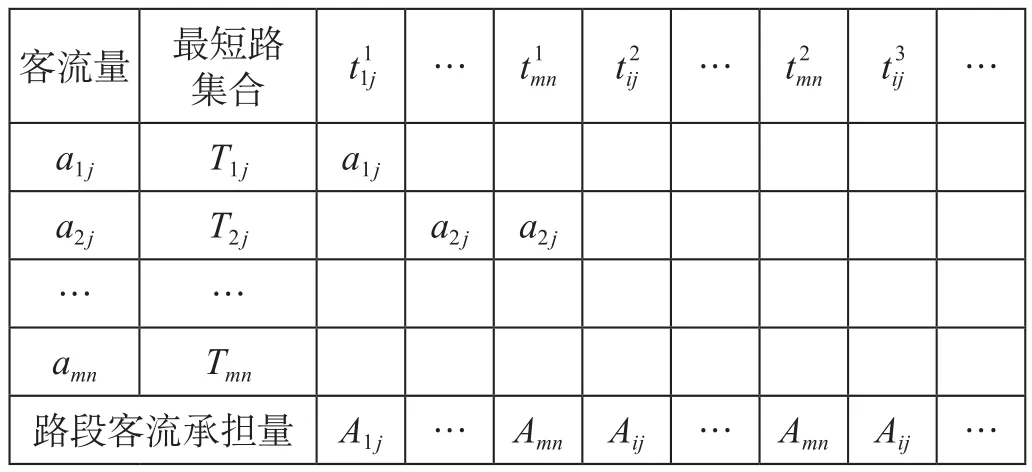
表2 路段客流承担量表样式Tab.2 Section passenger flow bearing table style

将相邻城市间的路段客流承担量及其最低广义运输成本按照(Aij，)的形式记录下来，从而得到计算所需的最小费用最大流基础图。多种交通方式协同优化最小费用最大流基础图如图3所示。

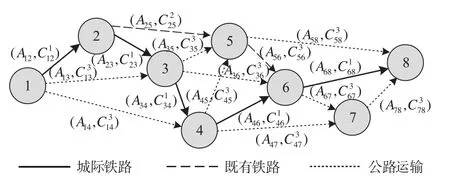
图3 多种交通方式协同优化最小费用最大流基础图Fig.3 Basic map of minimum cost maximum flow for collaborative optimization of multiple traffic modes

2.2 算法步骤

由于城际铁路及既有铁路在开行时，需从城市1始发至城市N终到，期间提供的运能一定，适用最小费用最大流的求解原则。而公路运输可从任意城市始发至周边城市终到，根据客流需求可直接求解开行方案，但不适用最小费用最大流的求解原则。故在计算的第1部分，即使用最小费用最大流理论计算时暂不考虑= 1的路段。在计算的第2部分即使用迭代算法计算时再加入此部分。多种交通方式协同优化最小费用最大流计算图如图4所示。

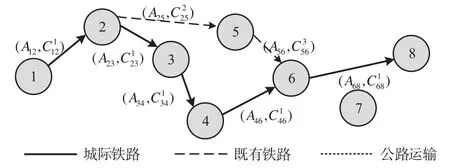
图4 多种交通方式协同优化最小费用最大流计算图Fig.4 Calculation of minimum cost maximum flow for collaborative optimization of multiple traffic modes

（1）计算第1部分。

步骤1：使用最小费用最大流理论解法求解出当前计算图的最小费用最大流。

步骤2：得到协同优化开行方案的基础开行数，并确定计算第2部分迭代算法的初始值。在计算基础开行数时可采用四舍五入的方法提高运输效率。

（2）计算第2部分。

步骤3：设还需增开n趟城际列车或m趟既有列车，并设n和m的初始值为0。

步骤4：调整图中弧容量，将铁路沿线可由公路运输改为铁路运输的客流需求进行调整。

步骤5：将剩余客流需求统一分配给各相邻城市间的公路运输。

步骤6：求解得出当前开行方案下目标函数z的值，记作znm。

步骤7：判断城际铁路及既有铁路线路上是否存在剩余客流需求未被满足，若存在则n=n+ 1或m=m+ 1，转至步骤4分别迭代1次，并记录成本较低的znm开行方案，以简化后期迭代；若不存在则转至步骤8。

（3）计算第3部分。

步骤8：求解出znm的最小值。

步骤9：确定出开行方案的可调开行数，得出非拥挤状态下城际间多种交通方式协同优化的开行方案，计算结束。

算法中步骤4所提到的可由公路运输改为铁路运输的客流需求是指某OD对间客流有多种交通方式可选，从广义运输成本角度公路运输的成本最低。但是，如果增开城际铁路或既有铁路，需将此部分客流需求从公路运输调整至城际铁路或既有铁路上来，从而提高城际间综合运输系统整体的运能利用率。

3 算例应用

以图1为例，对城市1至城市8上行方向的协同优化开行方案进行计算，以验证协同优化及其改进算法的有效性和准确性。

假定已知运输通道内相邻城市间多种交通方式的广义运输成本及各城市间OD客流，且在换乘时暂不考虑旅客换乘时间成本。成本及客流取值差异不影响模型计算过程及结果有效性，即利用该模型总能找到当前问题的最优协同开行方案，故算例按城际铁路、既有铁路、公路运输成本依次增大设置广义运输成本，依据大中小城市规模间出行数量依次减少设置OD客流，具体如下。

（1）城际铁路各OD点间的广义运输成本。城际铁路线路为：1→2→3→4→6→8。各段线路成本为：= 40元，= 30元，= 30元，= 30元，= 40元。

（2）既有铁路各OD点间的广义运输成本。既有铁路线路为：1→2→5→6→8。各段线路成本为：= 50元，= 60元，= 40元，= 50元。

（3）公路运输各OD点间的广义运输成本。公路广义运输成本如表3所示。

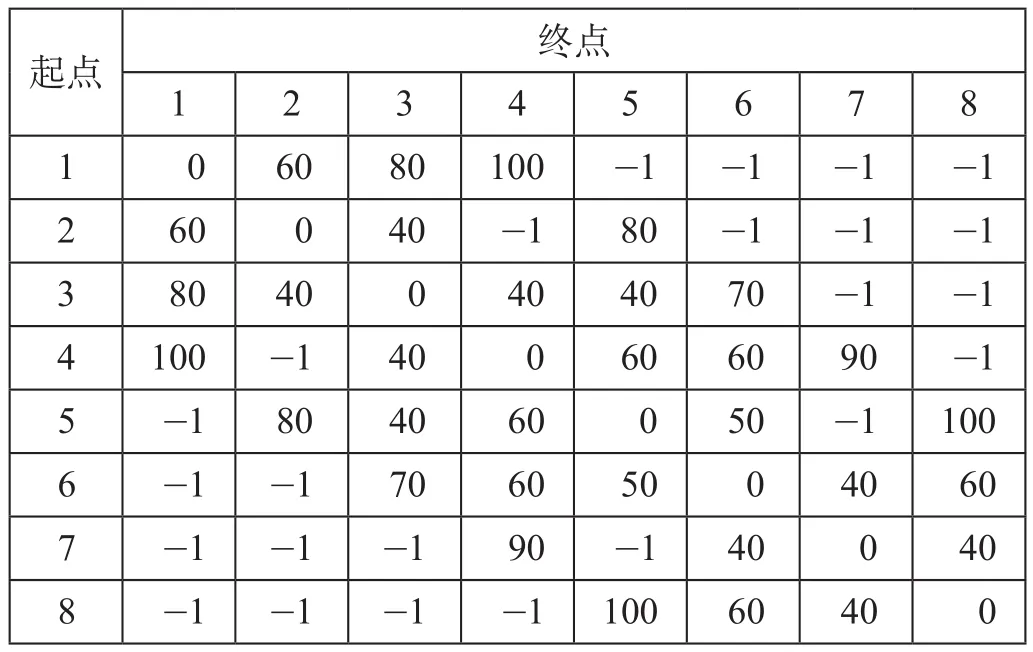
表3 公路运输广义运输成本表 元Tab.3 Generalized transport cost table for road transport

（4）OD调查上行客流量。OD调查上行客流量如表4所示。

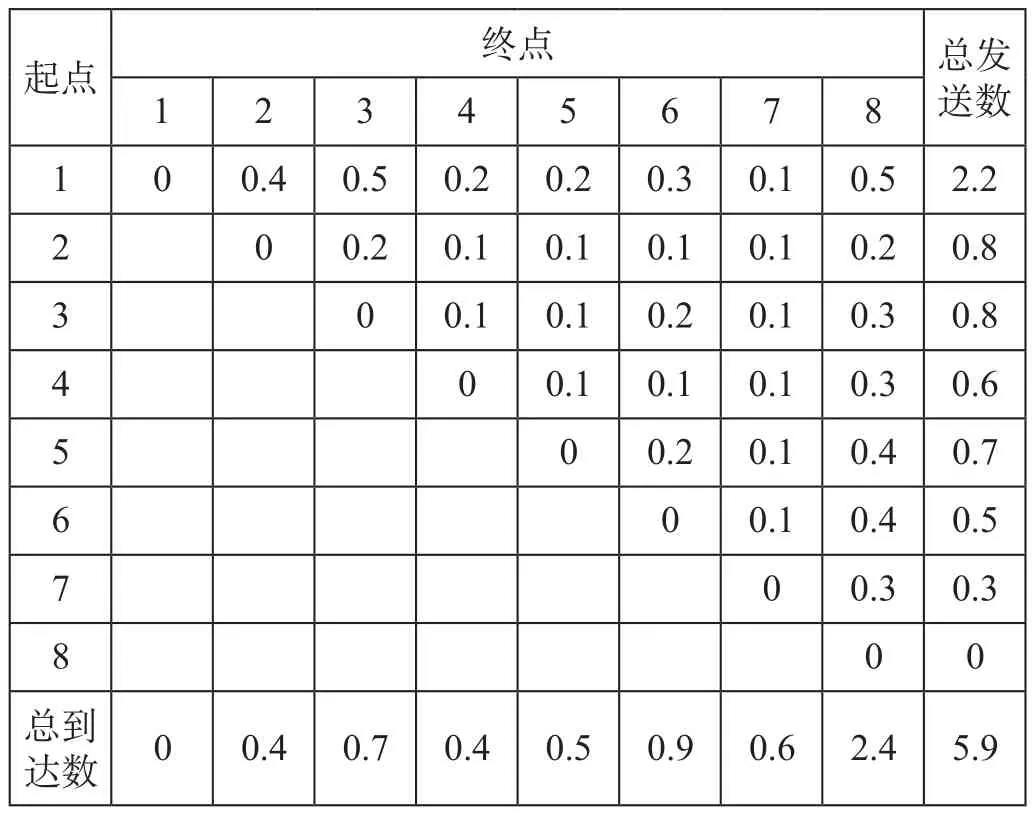
表4 OD调查上行客流量表 万人Tab.4 OD survey traffic flow at up direction

（5）多种交通方式的单位载客量。V1= 600，V2= 1 500，V3= 50。

通过已知数据可完成准备工作，首先使用Dijkstra算法得出各OD点间最短路集合，在此基础上，可计算出各OD点间路段客流承担量。其次计算出开行每列车的广义运输成本C1= 10.2万元/列，C2= 30万元/列。

在此基础上，通过第1部分算法，可计算出2种铁路交通方式的基础开行数= 32列= 1列。

通过第2部分算法，经11次迭代后，城际铁路及既有铁路线路上均不存在剩余客流需求，故迭代完成。其中在第7次迭代后，城际铁路线路上已不存在剩余客流，故不再参与迭代。

进入算法第3部分，比较11次迭代所得出的18种开行方案，可得minznm=z10= 499.3万元，相应可调开行数为= 1列，= 0列。故通过协同优化问题计算可得到3种交通方式的合理开行数分别为：L1= 33列，L2= 1列，= 24辆，= 40辆，= 30辆，= 20辆，= 40辆，= 20辆，= 44辆，= 110辆，= 120辆，= 60辆。

4 结束语

研究以城际铁路为主导的城际间运输通道内多种交通方式开行方案的协同优化，对有效降低旅客运输系统在非拥挤状态下的广义运输总成本具有重要意义。考虑广义运输成本及OD客流2个要素，将协同优化归纳为最小费用最大流问题，并依据其常用算法设计出协同优化改进算法以提高计算效率。协同优化结果为城际间运输通道内多种交通方式的日常开行方案提供了合理方案建议，在降低综合运输系统日常广义运输总成本的同时，可以促进多种交通方式间有序竞争，还可以对更大规模的城市群或更多种类的交通方式进行深入研究，考虑换乘成本等因素，探讨更加高效的算法。