求解大规模优化问题的分布式并行方法

余红蕾

(滁州城市职业学院 教育系，安徽 滁州239000)

1 引言

假设有两个很大的正整数n和m，考虑如下所示的一般带约束凸优化问题：

minimizief(x)

(1)

subject togk(x)≤0,∀k∈{1,2,…,m}

(2)

x∈χ

(3)

假设1：

·优化问题(1)-(3)存在唯一(可能不唯一)的最优解x*∈χ。

·存在Lf≥0，对于∀x,y∈χ，使‖f(x)-f(y)‖≤Lf‖x-y‖；对于k∈{1,2,…,m} ，存在Lgk≥0，对于∀x,y∈χ，使‖gk(x)-gk(y)‖≤Lgk‖x-y‖。令Lg=[Lg1,…,Lgm]T。

·存在β≥0，对于∀x,y∈χ，使‖g(x)-g(y)‖≤β‖x-y‖。

·存在C≥0，对于∀x∈χ，使‖g(x)‖≤C。

·存在R≥，对于∀x,y∈χ，使‖x-y‖≤R。

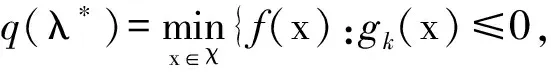
其中，q(λ)是优化问题(1)-(3)的拉格朗日对偶函数。

2 算法设计

2.1 大规模凸优化问题

问题(1)-(3)可以利用内点法(或牛顿法)来解决，这些方法需要在每次迭代的时候进行Hessian矩阵及其逆矩阵的计算。每次迭代的计算复杂度和内存空间复杂度在O(n2)和O(n3)之间。当n非常大时，计算和空间开销都是巨大的。例如，假设n=105，每个浮点数使用4字节储存，那么就需要用40 GB的内存来保存每次迭代的Hessian矩阵。因此，大规模的优化问题通常采用基于梯度或基于分解的方法进行求解。

2.2 Primal-Dual次梯度法

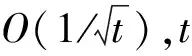
2.3 拉格朗日对偶方法

利用拉格朗日对偶方法求解问题(1)-(3)的收敛速度为O(1/t)[3]。如果函数f(x)和gk(x)具有可分解的结构，拉格朗日对偶方法可以将x(t)的计算分解为更小的子问题。但是，如果函数f(x)和gk(x)不可分解，则每次计算x(t)时都需要解一个有约束的凸优化问题，大大增加了计算的复杂度[4]。

2.4 一种新的算法

考虑一个大规模的凸优化问题，其中函数f(x)或者gk(x)不具有可以分解的结构。笔者通过结合Primal-Dual次梯度法和拉格朗日对偶方法的优点，提出了一种新的算法，其框架如下所示。

算法1 新的算法初始化:· 步长γ为正常数· 选择x(-1)∈χ· Qk(0)=max{0,-gk(x(-1))}对于每一个t:· 定义梯度d(t)=∇f(x(t-1))+∑mk=1[Qk(t)+gk(x(t-1))]∇gk(x(t-1))· 计算x(t)=Pχ[x(t-1)-γd(t)],其中,Pχ[g]是投影操作· 计算Qk(t+1)=max{-gk(x(t)),Qk(t)+gk(x(t))}· 计算x(t+1)=1t+1∑tτ=0x(τ)

3 基本分析

定义1：假设χ⊆n是一个凸集。若存在L>0，使‖h(y)-h(x)‖≤L‖y-x‖，那么函数h:→χ⊆m则具有利普希茨连续性。

定义2：假设χ⊆n，函数h(x)在χ上连续并可微。若h(x)在χ上是利普希茨连续，则函数h(x)在χ上是光滑的。

引理1[5]：若函数h在χ上是光滑的，那么有h(y)≤h(x)+

定义3：假设χ⊆n是一个凸集。若存在一个常数α>0，使在χ上是凸函数，则函数h在χ上是强凸函数。

引理2：假设χ⊆n是一个凸集。假设函数h是强凸函数，xopt是函数h在χ上全局最小解。那么，有

引理3：在算法1中，有

1) 在每一步迭代t∈{0,1,…}中，对于k∈{1,2,…,m}，Qk(t)≥0。

2) 在每一步迭代t∈{0,1,…}中，对于k∈{1,2,…,m}，Qk(t)+gk(x(t-1))。

3) 当t=0，‖Q(0)‖2≤‖g(x(-1))‖2；当t∈{1,2,…}，‖Q(t)‖2≥‖g(x(t-1))‖2。

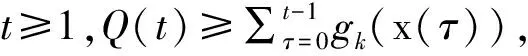
引理5：在每一个迭代t中，李雅普诺夫漂移的上界是

Δ(t)≤QT(t)g(x(t))+‖g(x(t))‖2

(4)

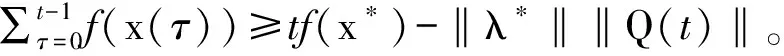
4 上界以及算法收敛分析

4.1 上界分析

引理7：假设x*是最优解。对于t≥0，有

证明：假设t≥0。令φ(x)=f(x)+[Q(t)+g(x(t-1))]T。由引理3的第二部分可知，Q(t)+g(x(t-1))中的每一个元素都是非负数。因此，φ(x)是凸函数。由于d(t)=φ(x(t-1))，算法1中的投影操作可以转化成以下的优化问题：

x(t)=Pχ[x(t-1)-γd(t)]

(5)

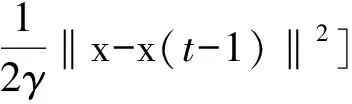
(6)

其中，(a)由函数φ(x)的凸性可得；(b)根据函数φ(x)的定义可得；(c)由引理3的第二部分可得。

由于函数f(x)在χ上是光滑的函数(假设1)，根据引理1，有

(7)

由假设1可知，每一个函数gk(x)在χ上都是光滑的。因此，[Qk(t)+gk(x(t-1))]gk(x)也是光滑的。由引理1，有

对上述不等式关于k∈{1,2,…,m}求和，得到

(8)

将公式(7)和(8)相加，得到

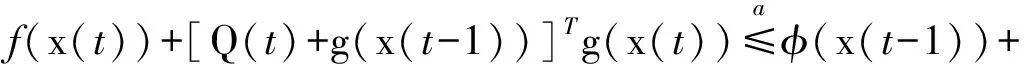
(9)

其中，(a)由函数φ(x)定义可得。

将公式(6)带入公式(9)，可得

(10)

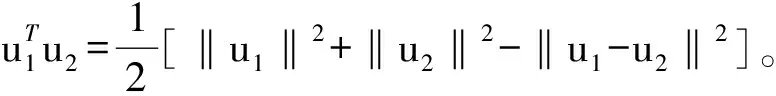
其中，(a)由‖g(x(t-1))-g(x(t))‖≤β‖x(t)-x(t-1)‖可得。将该不等式与公式(4)相加，能够得到

此时，引理7得证。

4.2 收敛速率

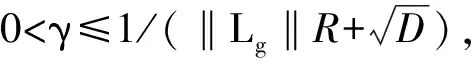
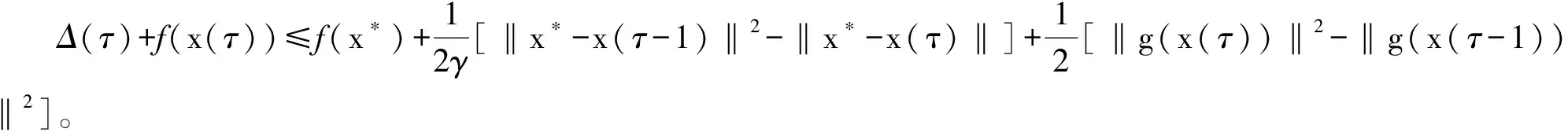
定理1说明了算法1的误差以速度O(1/t)减少，即算法1的收敛速率是O(1/t)。

5 结论

针对大规模的凸优化问题，提出了一种新的具有更快收敛速度的原对偶方法，每次迭代仅需要进行简单的梯度更新，从而降低复杂度。未来的工作将探讨如何在真实的应用场景实现笔者提出的算法。