三维各向异性油藏水平井产能新公式

贾晓飞 ，雷光伦 ，孙召勃 ，姚传进

（1.中国石油大学（华东）石油工程学院，山东青岛266580；2.中海石油（中国）有限公司天津分公司渤海石油研究院，天津300459）

水平井能够有效提高生产井段与储层的接触面积，增大泄油半径以及渗流面积，大幅度提高单井产能和采收率，广泛应用于实际油田开发中［1-5］。水平井产能是水平井部署决策的重要技术指标，而目前常规水平井产能公式只考虑了外部平面径向流和内部垂向径向流，预测结果往往偏高［6-13］。事实上，水平井的渗流机理较复杂，不仅包括外部平面径向流和内部垂向径向流，还包括中间平面线性流［14-15］，传统方法预测结果偏大的重要原因就是对中间平面线性流的忽视。近年来，诸多学者充分考虑这3种渗流形态，推导建立了均质油藏的综合形式的水平井产能预测公式［16-19］，也有学者通过平面和纵向的二维异性对公式进行了校正［20-21］，并没有考虑平面的各向异性。大量研究和开发实践表明，不同沉积环境下，由于物源方向、水动力条件不同，沉积过程中岩石颗粒大小不同且其空间排列方式各异，从而导致油藏不同方向的渗透率不同［22-28］。在对水平井产能进行计算评价时必须考虑各向异性的影响，尤其是平面各向异性与水平井部署方位的配置关系对水平井的产能影响较为显著。

为此，笔者通过坐标变换将三维各向异性油藏转换为等效的各向同性油藏，在此基础上，利用水电相似原理和等值渗流阻力方法，推导出了考虑油藏三维各向异性和平面线性流的水平井产能计算新公式，可以对三维各向异性油藏不同方位部署的水平井的产能进行预测。

1 三维各向异性等效转换

假设一个三维各向异性油藏上、下边界封闭，主渗透率方向与坐标轴方向平行（图1），油藏厚度为h，泄油半径为 re，x，y，z方向的渗透率分别为 Kx，Ky，Kz，水平井长度为L，井筒半径为rw，与坐标轴x夹角为α。

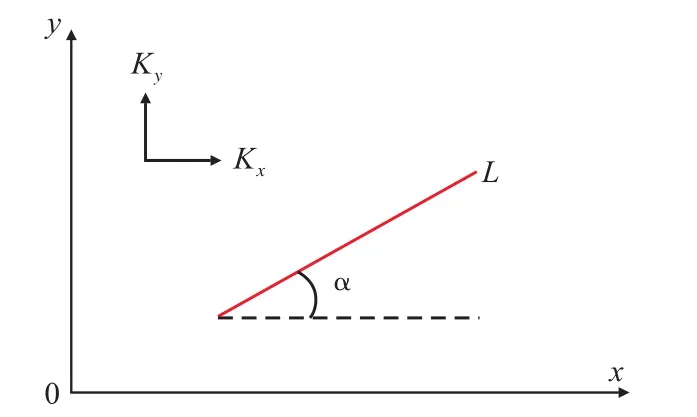
图1 各向异性油藏水平井平面示意Fig.1 Schematic planar diagram of horizontal wells in anisotropic reservoir

定义变量分别为：

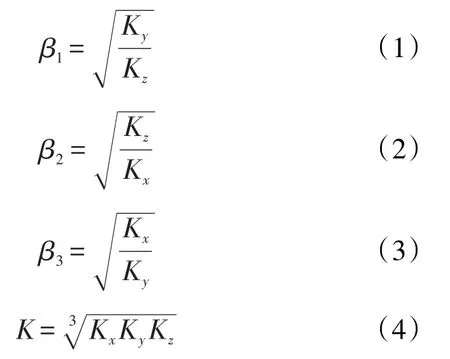
通过坐标变换将三维各向异性油藏等效变换为各向同性油藏的方程式分别为：

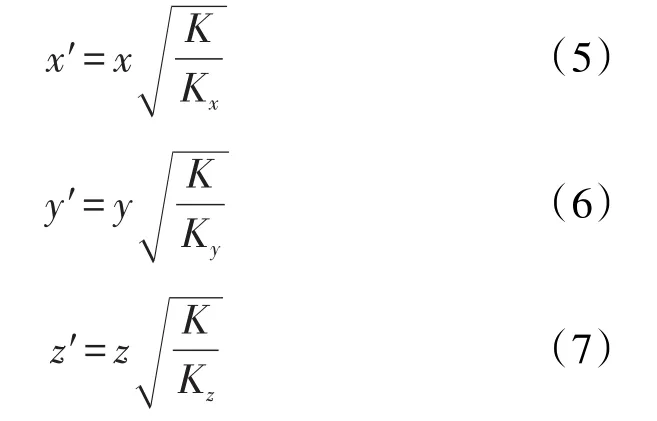
经过坐标变换后，原来各向异性油藏oxy平面内的问题转换为各向同性油藏o′x′y′平面内的问题，平均渗透率为K，厚度变换为h′，水平井长度变换为L′，井筒半径变换为rw′，与坐标轴 x′夹角为 α′，则o′x′y′平面内的油藏及水平井参数为：

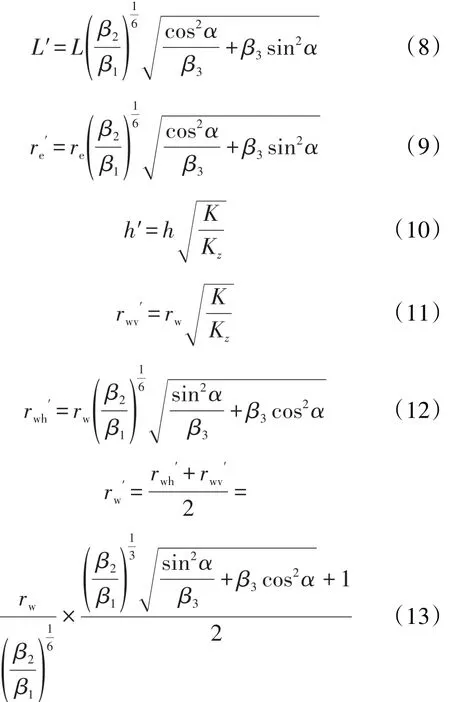
2 水平井产能新公式推导

水平井在油藏的渗流主要包括以下3种形态：远离水平井区域的外部平面径向流（图2a）、靠近水平井区域的中间平面线性流（图2b）以及水平井周围小范围的内部垂向径向流（图2c）。

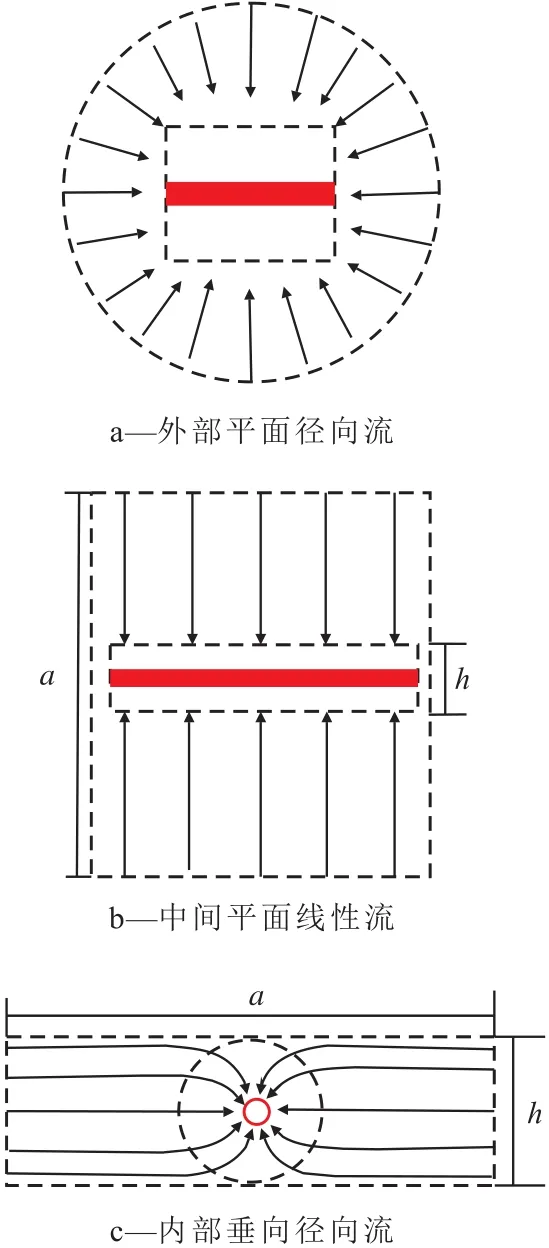
图2 水平井3种主要渗流形态示意Fig.2 Schematic planar diagramof three main seepage patterns in horizontal wells

不同渗流区域的渗流形态不同，所对应的渗流阻力［17-21］也不同。

对于外部平面径向流，渗流区域的外边界为水平井的泄油半径，内边界半径为水平井的半长，可得渗流阻力方程为：

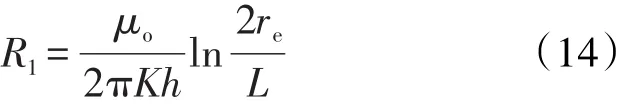
对于中间平面线性流，渗流区域的长度为水平井的长度，由于渗流区域的面积等效于半径为水平井半长的圆形区域面积，即可得渗流区域的宽度为：

所以，中间平面线性流的渗流阻力方程为：

对于内部垂向径向流，外边界半径为油层厚度之半，内边界半径（水平井井筒半径）为rw，可得渗流阻力方程为：

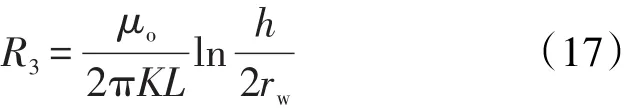
因此，水平井总渗流阻力方程为：

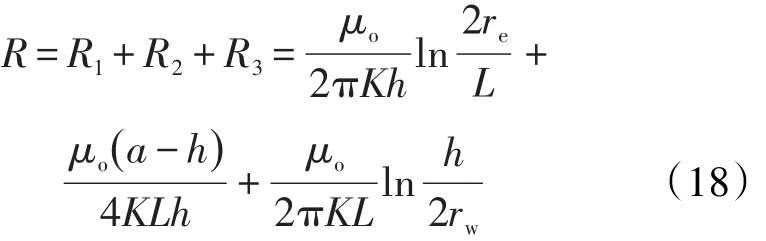
在地面条件下，均质油藏综合形式水平井产能公式为：

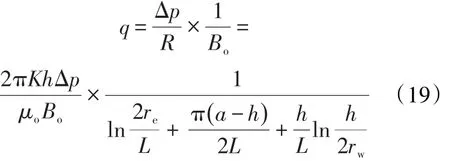
三维各向异性校正后的水平井总渗流阻力方程为：

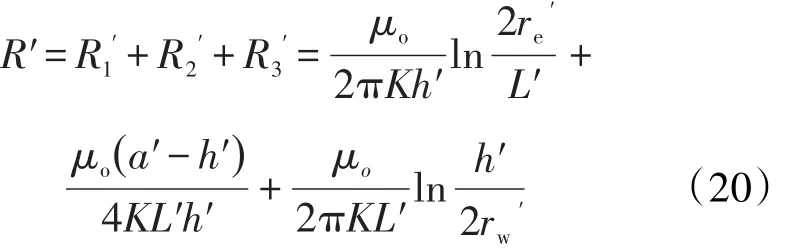
因此，三维各向异性油藏综合形式水平井产能新公式为：

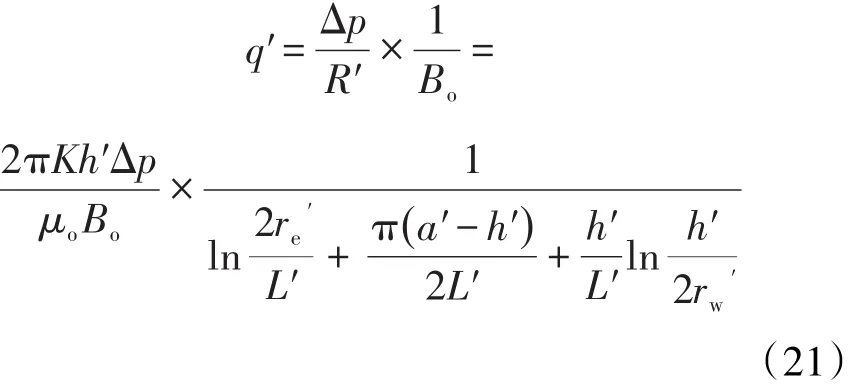
3 产能公式对比及各向异性影响因素分析

3.1 不同产能公式对比

对于各向同性的均质油藏，当忽略毛细管力、重力和弹性膨胀的影响，达西稳定渗流条件下，常用的有以下3种水平井产能公式［29］。

Borisov公式［9］为：

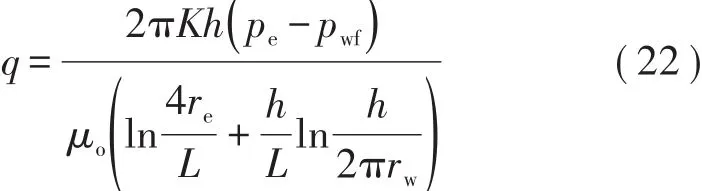
Giger-Resis-Jourdan 公式［8］为：

（22）式—（24）式未考虑油藏的各向异性，且只考虑了外部平面径向流和内部垂向径向流及其渗流阻力，并未考虑靠近水平井区域的中间平面线性流及其渗流阻力。与目前常规水平井产能公式（Borisov公式、Giger-Resis-Jourdan公式、Joshi公式）相比，建立的三维各向异性油藏综合形式水平井产能新公式既考虑了所有渗流形态，又考虑了油藏的三维各向异性。

3.2 不同产能公式计算结果对比

已知的油藏基本参数为：泄油面积为1×106m2，水平井井筒半径为0.1 m，三维各向异性油藏x，y，z方向的渗透率分别为2 000，1 000和100 mD，油层厚度为10 m，纵向上垂直于井筒方向的底部渗流边界到井筒中心的距离为5 m，地层原油黏度为3.0 mPa·s，原油体积系数为 1.00 m3/m3，生产压差为 1.0 MPa。计算可以得到平面等效渗透率为1 414 mD。当水平井与x轴夹角为45°时，由（21）式—（24）式可以得到不同水平段长度下水平井产能公式的计算结果（图3），不同产能公式计算的水平井产能不尽相同。

由图3可知：①水平井产能随着水平段长度的增加而增大。分析认为，这主要是由于水平段长度越长，水平井控制储量的范围及泄油面积越大，水平井的产能越高。②随着水平段长度的增加，目前常规水平井产能公式与建立的三维各向异性油藏综合形式水平井产能新公式的计算结果偏差增大。当水平井长度小于200 m时，4种方法的水平井产能计算结果较为接近；当水平井长度超过200 m后，目前常规水平井产能公式与建立的三维各向异性油藏综合形式水平井产能新公式的计算结果偏差逐渐增大，表现为目前常规水平井产能公式计算结果偏高。分析认为，这主要是因为油藏渗透率的三维各向异性不可忽略，且随着水平井长度的增加，水平井平面线性流的范围越来越大，目前常规水平井产能公式未考虑油藏的非均质性及平面线性流带来的渗流阻力，因此计算结果偏高，而建立的三维各向异性油藏综合形式水平井产能新公式充分考虑了油藏的各向异性及平面线性流及其渗流阻力，计算结果更合理。

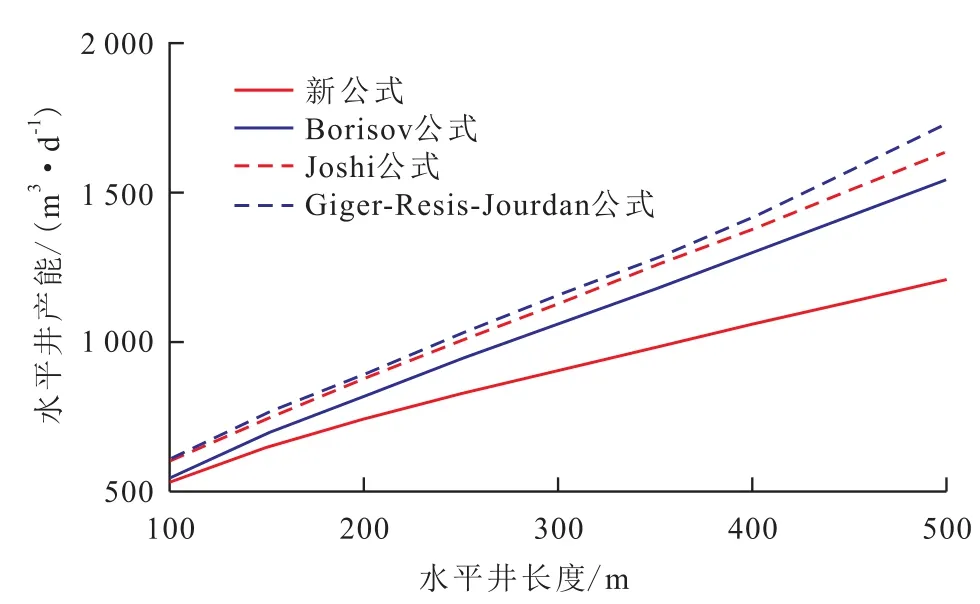
图3 不同水平井产能公式计算结果对比Fig.3 Comparison of calculation results fromdifferent horizontal well productivity formulas

3.3 各向异性影响因素

平面各向异性 当水平井长度为300 m，平面等效渗透率为1 414 mD时，设置不同的Kx和Ky，其他基础参数不变，计算不同水平井方位下的平面各向异性对水平井产能的影响（图4）。

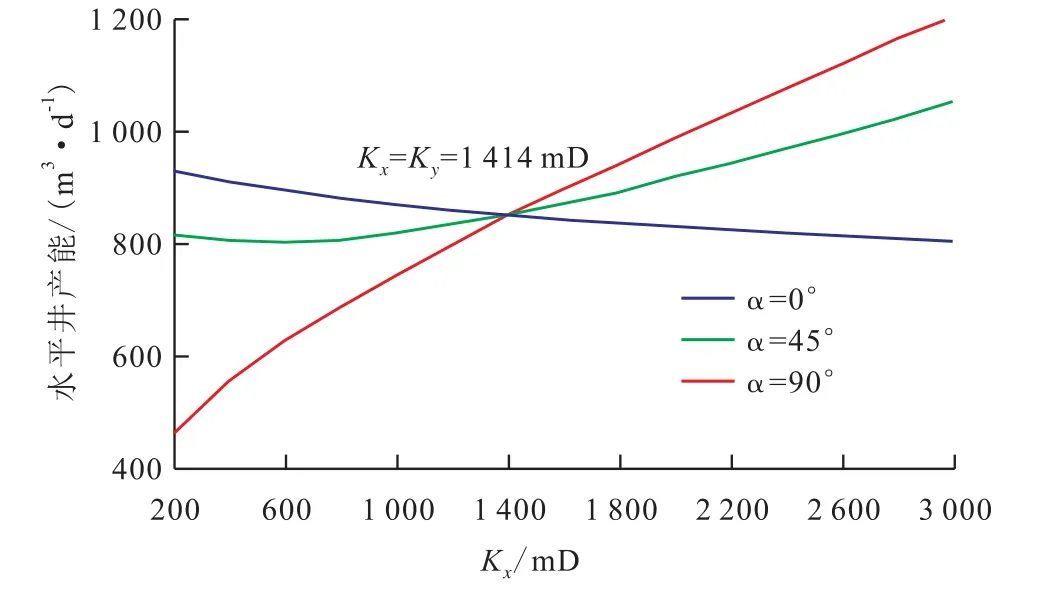
图4 平面各向异性对水平井产能的影响Fig.4 Effect of planar anisotropy on horizontal well productivity

由图4可知，平面各向异性对水平井产能影响较明显，不同水平井方位下渗透率对产能的影响规律也不同。当α=0°时，即水平井井筒平行于x轴时，随着Kx的增加，水平井产能逐渐降低；当α=90°时，即水平井井筒垂直于x轴时，随着Kx的增加，水平井产能逐渐增加；当α=45°时，即水平井井筒和x轴成45°夹角时，随着Kx的增加，水平井产能先下降后增加。其原因为水平井井筒越接近垂直主渗透率方向，主渗透率越大，则渗流阻力越小，产能越高。

垂向各向异性 当水平井长度为300 m、水平井井筒与x轴夹角为45°时，保持其他基础参数不变，设置不同的Kz值，计算垂向各向异性对水平井产能的影响。由图5可知，平面渗透率一定时，水平井产能随着垂向渗透率的增加而增大。分析认为，这主要是因为油藏中的垂向渗透率远小于平面渗透率，随着垂向渗透率的增大，油藏各向异性程度逐渐变小，水平井产能逐渐增加。

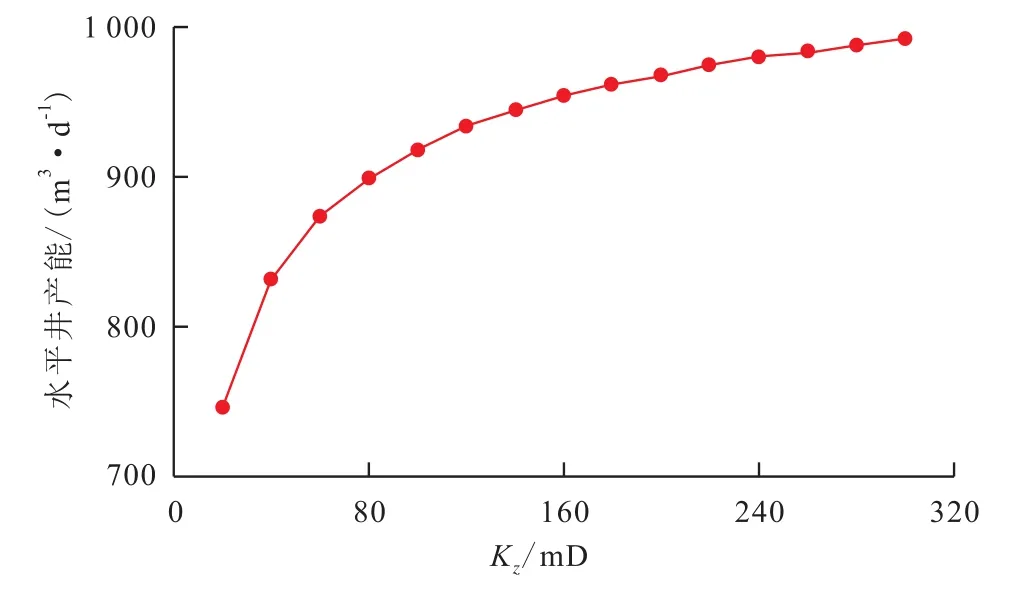
图5 垂向渗透率对水平井产能的影响Fig.5 Effect of vertical permeability on horizontal well productivity

水平井方位 当水平井长度为300 m时，保持其他基础参数不变。研究各向异性油藏中水平井方位对水平井产能的影响。

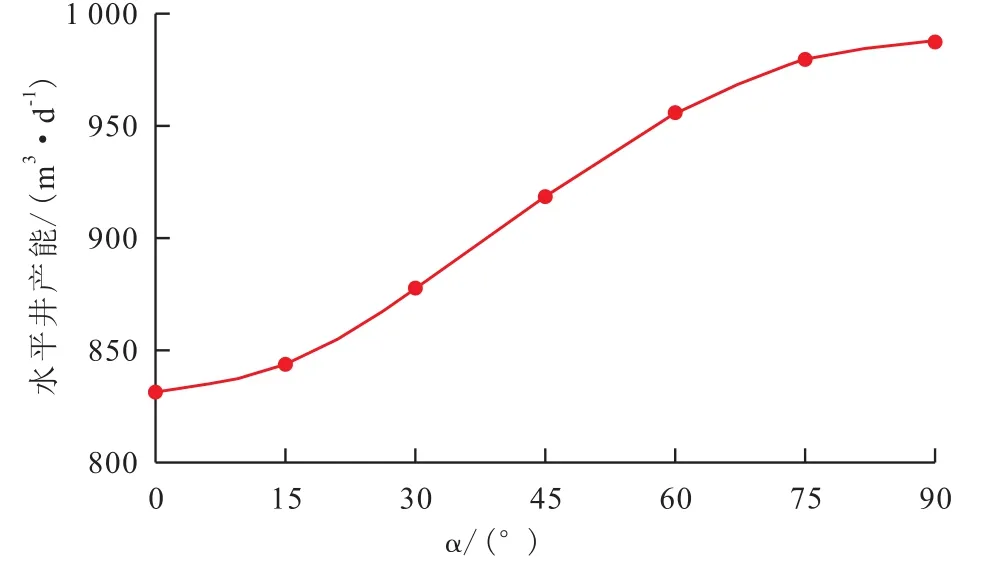
图6 水平井方位对产能的影响Fig.6 Effect of azimuth valueαon horizontal well productivity

由图6可以看出，水平井与油藏主渗透率方向的夹角对产能的影响显著，随着水平井方位的增加，水平井产能逐渐增加，当水平井井筒垂直主渗透率方向（α等于90°）时产能最高，约为平行于主渗透率方向（α等于0°）时产能的1.2倍。这是因为水平井井筒垂直于主渗透率方向时，油藏向水平井井筒的供液方向与主渗透率方向相同，此时的渗流阻力最小。

4 实例计算与分析

以渤海SZ油田2017年实施的水平井X8H1为例，基础参数包括：油层厚度为5 m，水平井位于储层中央，泄油面积为12.25×104m2，油藏顺物源方向渗透率为4 000 mD，垂直物源方向渗透率为2 857 mD，垂向渗透率为338 mD，地层原油黏度为100 mPa·s，原油体积系数为 1.08 m3/m3，水平井垂直物源方向布井，水平段长度为260 m，井筒半径为0.1 m，生产压差为2.4 MPa。利用该实例对三维各向异性油藏综合形式水平井产能新公式及目前常规水平井产能公式（Borisov公式、Giger-Resis-Jourdan公式、Joshi公式）进行对比分析。X8H1井实际初期产能为132 m3/d。Borisov公式计算的产能为200 m3/d，与实际产能的误差为51.5%；Giger-Resis-Jourdan公式计算的产能为246 m3/d，误差为86.4%；Joshi公式计算的产能为187 m3/d，误差为41.4%；建立的三维各向异性油藏综合形式水平井产能新公式计算的产能为136 m3/d，误差仅为3.0%。由计算结果可知，Giger-Resis-Jourdan公式的误差最大，三维各向异性油藏综合形式水平井产能新公式的误差最小。

通过研究分析可知，X8H1井部署的油藏非均质性较强，不能够按照各向同性的均质油藏处理；另外，水平井长度超过200 m，水平井平面线性流的范围增大，计算产能时不能忽略平面线性流所带来的渗流阻力。目前常规水平井产能公式均未考虑油藏各向异性及平面线性流所带来的渗流阻力，导致所计算的渗流阻力偏小，产能预测结果偏高；而三维各向异性油藏综合形式水平井产能新公式考虑因素更全面，更加符合实际油藏三维各向异性的特点以及水平井的渗流特征，计算结果与实际水平井产能更为接近，预测结果更准确。

5 结论

根据实际油藏三维各向异性的特点以及水平井的渗流特征，建立三维各向异性油藏综合形式水平井产能新公式。该公式综合考虑油藏三维各向异性和水平井平面线性流特征对水平井产能的影响，能够更加准确地评价水平井产能。不论水平段长度多长，油藏三维各向异性均会严重影响水平井产能，要准确评价水平井产能，必须考虑三维各向异性的影响；而随着水平井长度的增加，水平井的渗流形态会发生变化，平面线性流的范围越来越大，且其所带来的渗流阻力对水平井产能的影响也增大，不可忽略。

符号解释：

h——油藏厚度，m；re——泄油半径，m；x,y,z——三维各向异性油藏平面主渗透率方向坐标；Kx,Ky,Kz——三维各项异性油藏x,y,z方向的渗透率，mD；L——水平井长度，m；rw——水平井井筒半径，m；α——水平井与坐标轴x夹角，（°）；β1——y与z方向渗透率比值系数；β2——z与x方向渗透率比值系数；β3——x与y方向渗透率比值系数；K——平均渗透率，mD；x′——坐标变换后的等效各向同性油藏平面主渗透率方向坐标；y′——坐标变换后的等效各向同性油藏平面垂直主渗透率方向坐标；z′——坐标变换后的等效各向同性油藏垂向渗透率方向坐标；h′——坐标变换后的等效各向同性油藏的油层厚度，m；L′——坐标变换后的等效各向同性油藏的水平井长度，m；rw′——坐标变换后的等效各向同性油藏的井筒半径，m；α′——坐标变换后的等效各向同性油藏的水平井与坐标轴 x′夹角，（°）；re′——坐标变换后的等效各向同性油藏的泄油半径，m；rwv′——坐标变换后的等效各向同性油藏的垂向井筒半径，m；rwh′——坐标变换后的等效各向同性油藏的平面井筒半径，m；R1——外部平面径向流渗流阻力，MPa·d/m3；μo——地层原油黏度，mPa·s；a——渗流区域宽度，m；R2——中间平面线性流渗流阻力，MPa·d/m3；R3——内部垂向径向流渗流阻力，MPa·d/m3；R——水平井的总渗流阻力，MPa·d/m3；q——均质油藏综合形式水平井产能，m3/d；Δp——总生产压差，MPa；Bo——地层原油体积系数，m3/m3；R′——三维各向异性校正后的水平井总渗流阻力，MPa·d/m3；R1′——三维各向异性校正后的外部平面径向流渗流阻力，MPa·d/m3；R2′——三维各向异性校正后的中间平面线性流渗流阻力，MPa·d/m3；R3′——三维各向异性校正后的内部垂向径向流渗流阻力，MPa·d/m3；a′——三维各向异性校正后的渗流区域宽度，m；q′——三维各向异性油藏综合形式水平井产能，m3/d。