大气PM2.5中多环芳烃浓度缺失值填补方法的研究

王燚烊 王瑞福 武建辉△

【提 要】 目的 研究大气PM2.5中多环芳烃(PAHs)浓度缺失值的填补方法。方法 采用Pearson相关分析16种∑PAHs浓度与气象因素及大气污染物的相关关系；采用Box-Cox变换、多元线性逐步回归法和曲线拟合法拟合回归方程，将缺失的16种∑PAHs浓度作为因变量，相关变量作为自变量，以预测值作为PAHs浓度填补值。结果 16种∑PAHs浓度与平均温度、风速和日照小时数呈负相关，与平均相对湿度和平均气压呈正相关，与PM2.5、PM10、SO2、NO2浓度呈正相关，与O3呈负相关。气象因素中平均温度对16种∑PAHs浓度影响最大，大气污染物中PM2.5对16种∑PAHs浓度影响最大，回归方程预测的2017年16种∑PAHs浓度与实测的比较，结果显示均无差别。结论 对数据Box-Cox变换后采用多元线性逐步回归法建立16种∑PAHs浓度与平均温度和平均风速的回归方程，回归模型拟合效果较好，可用来填补缺失的PAHs浓度。

随着空气污染的加剧，大气PM2.5中的多环芳烃(PAHs)由于具有随颗粒物远距离迁移的特征，而受到了国内外学者的关注，很多地区都开展了大气中PAHs浓度的监测[1]，国内大气PM2.5中PAHs对人群健康影响的研究受到广泛关注[2]。而在PAHs浓度的收集过程中缺失数据是不可避免的，如果忽略缺失数据，直接把获得观测值的先后顺序当作时间顺序来建模，势必会得到错误的拟合模型[3]。

填补法是对各种填补措施的总结概括，常见的填补法有替代法和建模估计法[3]。唐山市的路北监测点由于时间和条件的限制，样品的采集不是逐日开展的，为填补PAHs浓度缺失值，采用Box-Cox变换、多元线性逐步回归法和曲线拟合法拟合方程填补缺失的PAHs浓度。

材料与方法

1.资料来源

(1)PAHs浓度 PAHs浓度数据来源于2015年1月-2017年12月唐山市路北监测点,在固定采样日(每月10～16日)和霾日(AQI>200)进行PM2.5采样，利用高效液相色谱法成分分析得到PAHs的浓度。

(2)大气污染物浓度 同期的大气污染物浓度资料来源于唐山市6个国控大气环境监测站点，由唐山市环境保护局监测。

(3)气象资料 同期气象数据来源于唐山市气象局，主要包括平均气压(hpa)、平均温度(℃)、日平均风速(m/s)、平均相对湿度(%)和日照小时数(h)。

2.统计学方法

用SPSS 19.0和R 3.4.4软件进行统计分析；Pearson相关分析16种PAHs浓度与气象因素和大气污染物的相关性；利用Box-Cox变换、多元线性逐步回归法和曲线拟合法拟合回归方程，将缺失变量PAHs浓度作为因变量，相关变量为自变量，以预测值作为PAHs浓度填补值，对未监测的PAHs浓度进行填补。

结 果

1.相关性分析

表1为2015-2016年PAHs浓度与气象因素和大气污染物之间的Pearson相关系数。结果显示，PAHs浓度与平均温度、风速之间呈负相关，与平均相对湿度和平均气压之间呈正相关；与PM2.5、PM10、SO2、NO2浓度呈正相关，与O3呈负相关。

2.路北监测点16种∑PAHs浓度与气象因素的多元线性逐步回归方程

(1)16种∑PAHs浓度与气象因素的多元线性逐步回归方程

多元线性逐步回归分析2015年1月-2016年12月气象因素与16种∑PAHs浓度的关系，运用逐步法，α入=0.10，α出=0.15，最后筛选进入方程的是平均温度和平均风速。直线方程为：

Y1=307.999-7.718X1-50.463X2

式中Y1表示16种PAHs总浓度，ng/m3；X1表示平均温度，℃；X2表示风速，m/s。

结果显示，拟合的回归方程有统计学意义(P<0.05)。X1的标准化回归系数为-0.577，X2的标准化回归系数为-0.305，说明平均温度对16种多环芳烃总浓度影响最大。

(2)Box-Cox变换后16种∑PAHs浓度与气象因素的多元线性逐步回归方程

表1 PAHs与大气污染物和气象因素之间的Pearson相关系数

注：a为P<0.01;b为P<0.05；c为P>0.05

对因变量Y进行Box-Cox变换，不同取值λ(-2≤λ≤2)，用R中的boxcox函数采用最大似然估计法进行估计[4]，计算其似然函数的最大值ln(Lmax(λ))，图1为似然函数的最大值ln(Lmax(λ))随λ变化的曲线，结果显示：λ=0时，ln(Lmax(λ))的值最大。

图1 似然函数的最大值ln(Lmax(λ))随λ变化的曲线

根据似然原理，λ=0时为对数变换，对因变量Y经Box-Cox变换后的数据再次进行多元线性逐步回归分析[5]，回归方程为：

(3) Box-Cox变换后建立的16种∑PAHs浓度与气象因素方程的回归诊断

图2为Box-Cox变换后建立的16种∑PAHs浓度与气象因素方程的回归诊断结果，结果显示，变换后建立的回归方程满足正态性的假设，满足方差齐性的条件。

3.路北监测点16种∑PAHs浓度与大气污染物的多元线性逐步回归方程

(1) 16种∑PAHs浓度与大气污染物的多元线性逐步回归方程

多元线性逐步回归分析2015年1月-2016年12月16种∑PAHs浓度与大气污染物的关系，α入=0.10，α出=0.15，最后筛选进入方程的是PM2.5、PM10、O3和SO2。直线方程为：

Y2=153.151-0.152X3+0.42X4-0.269X5+0.141X6

图2 Box-Cox变换后16种∑PAHs浓度与气象因素方程的回归诊断

式中Y2表示路北监测点16种多环芳烃总浓度，ng/m3；X3表示O3，μg/m3；X4表示PM2.5，μg/m3；X5表示PM10，μg/m3；X6表示SO2，μg/m3。

结果显示，拟合的回归方程有统计学意义(P<0.05)。X3的标准化回归系数为-0.368，X4的标准化回归系数为1.267，X5的标准化回归系数为-1.084，X6的标准化回归系数为0.171，说明PM2.5对16种多环芳烃总浓度影响最大。

(2) Box-Cox变换后16种∑PAHs浓度与大气污染物浓度的多元线性逐步回归方程

对因变量Y进行Box-Cox变换，图3为似然函数的最大值ln(Lmax(λ))随λ变化的曲线，结果显示：λ=0时，ln(Lmax(λ))的值最大。

图3 似然函数的最大值ln(Lmax(λ))随λ变化的曲线

对因变量Y经Box-Cox变换后的数据再次进行多元线性逐步回归分析，回归方程为：

(3) Box-Cox变换后建立的16种∑PAHs浓度与大气污染物浓度方程的回归诊断

图4为Box-Cox变换后建立的16种∑PAHs浓度与大气污染物回归方程的回归诊断结果，结果显示，Box-Cox变换后建立的多元线性回归方程满足正态性的假设，方差齐。

4.曲线拟合法建立路北监测点16种∑PAHs 浓度与平均温度的方程

(1) 平均温度与路北监测点16种∑PAHs的回归方程

直线回归分析2015年1月-2016年12月路北监测点16种∑PAHs浓度与平均温度的关系，直线方程为：

Y3=201.444-8.217X7

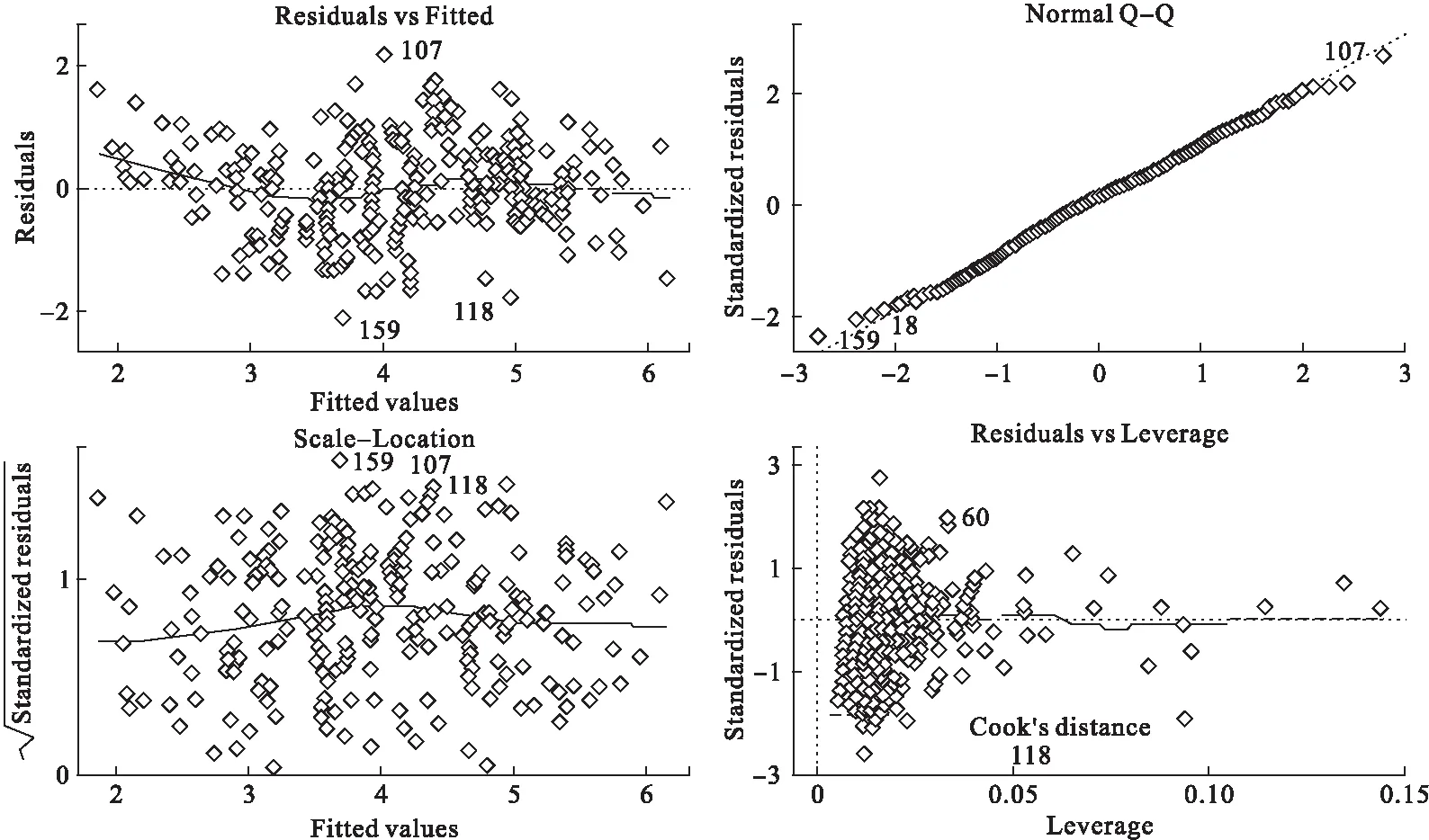
图4 Box-Cox变换后16种∑PAHs浓度与大气污染物浓度方程的回归诊断

式中Y3表示路北监测点16种多环芳烃总浓度，ng/m3；X7表示平均温度，℃。

(2) Box-Cox变换后16种PAHs浓度与平均温度的回归方程

对因变量Y进行Box-Cox变换，图5为似然函数的最大值ln(Lmax(λ))随λ变化的曲线，结果显示：λ=0时，ln(Lmax(λ))的值最大。

根据似然原理，λ=0时为对数变换，对因变量Y经Box-Cox变换后的数据再次进行直线回归分析[5]。回归方程为：

图5 似然函数的最大值ln(Lmax(λ))随λ变化的曲线

回归方程的方差分析显示，拟合的回归方程有统计学意义(P<0.001)。对回归系数进行假设检验，回归系数也有统计学意义(P<0.001)。

(3) Box-Cox变换后建立的16种∑PAHs浓度与平均温度回归方程的回归诊断

图6为Box-Cox变换后建立的16种∑PAHs浓度与平均温度的直线回归方程的回归诊断结果，结果显示，Box-Cox变换后建立的回归方程满足正态性的假设，满足方差齐性的条件。

图6 Box-Cox变换后16种∑PAHs浓度与平均温度方程的回归诊断

5.Box-Cox变换前后建立的回归方程回归分析结果比较

表2为 Box-Cox变换前后采用多元线性逐步回归法和直线回归法建立的回归方程的回归分析结果比较，结果显示，经Box-Cox变换后，决定系数(R2)升高，对数据变换后建立的回归方程的效果好于变换前建立的回归方程。

表2 Box-Cox变换前后建立的回归方程的回归分析结果比较

6.Box-Cox变换后建立的回归方程预测值与实测值的比较

表3为Box-Cox变换后多元线性逐步回归法和直线回归法建立的回归方程预测的2017年固定采样日(每月10～16日)和霾日(AQI>200)的16种∑PAHs浓度与路北监测点实测的16种∑PAHs浓度的比较，经Kruskal-wallis H检验，P=0.154>0.05，按α=0.05检验水准，尚不能拒绝H0，差别无统计学意义，即Box-Cox变换后建立的方程预测的16种∑PAHs浓度与监测点实测的16种∑PAHs浓度均无差别。

表3 不同方程预测与实测的PAHs浓度的比较

讨 论

16种∑PAHs浓度与平均温度、风速和日照小时数之间呈负相关关系，与平均相对湿度和平均气压之间呈正相关关系，温度高、日照时间长都会加速多环芳烃的分解，风速高会不利于多环芳烃的沉积[6]，这与本研究16种∑PAHs浓度均与平均温度、风速和日照小时数之间呈负相关关系结果一致。大气中的PAHs主要以可吸入颗粒物和气相的形式吸附在颗粒物或者在大气飘尘中，空气中的PAHs与氧气、臭氧或其他氧化剂反应生成内环过氧化物[7]。PAHs浓度与PM2.5、PM10、SO2、NO2浓度呈正相关关系，与O3呈负相关结果一致。

将缺失变量16种∑PAHs浓度作为因变量，相关变量作为自变量，采用多元线性逐步回归法和直线回归法对因变量Y经Box-Cox变换前后拟合回归方程。直线回归方程显示，大气污染物中PM2.5对16种∑PAHs浓度影响最大；气象因素中平均温度对16种∑PAHs浓度影响最大[7]。研究表明，影响大气中的 PAHs存在状态的因素包括PAHs的理化性质、气象因素、其他污染物(如PM10、SO2、NO2)等[8]。Callén等人利用多元线性回归模型，用气象因素和PM10浓度作为可能的预测指标能较好的模拟出空气中PAHs浓度[9]。Mehmet等人也利用多元回归分析预测PAHs与气象因素和颗粒物浓度的关系，结果显示，温度对PAHs浓度影响较大，而相对湿度和气压影响相对较小，利用方程预测和实测的PAHs年均浓度相近，可以较好的说明多元回归模型可用于PAHs浓度和相关因素的预测[10-11]。

对因变量Y经Box-Cox变换后采用多元线性逐步回归法和直线回归法预测得到2017年固定采样日(每月10-16日)和霾日(AQI>200)的16种∑PAHs浓度与监测点实测的16种∑PAHs浓度进行比较，结果显示，建立的方程预测的16种∑PAHs浓度与路北监测点实测的16种∑PAHs浓度均无差别。因变量Y经Box-Cox变换后采用多元线性逐步回归法建立的回归方程拟合效果优于Box-Cox变换前建立的回归方程，而且采用多元线性逐步回归法和曲线拟合法建立回归方程较为简单易行，可操作性强，能更直接的说明PAHS浓度与气象因素和大气污染物浓度之间的关系。因变量Y经Box-Cox变换后采用多元线性逐步回归法拟合的PAHS浓度与平均温度和风速的回归方程效果较好(R2=0.742)，能较好的预测16种∑PAHs浓度。可以用Box-Cox变换和多元线性逐步回归法拟合16种∑PAHs浓度与平均温度和风速的方程，然后用预测值来填补未监测日期的16种∑PAHs浓度。