基于可验证SM2门限算法的移动终端签名系统的设计与实现
2019-03-19,,
,,
(1.西南科技大学 计算机科学与技术学院,四川 621010; 2.北京市公安局 昌平分局警务支援大队,北京 102200)
0 引言
伴随着移动互联网的快速发展、智能手机迅速普及,各种移动互联网业务也迅速发展,如移动电子商务、手机支付、手机阅读、手机游戏、手机证券等[1]。移动端作为一个开放性的轻量级设备,在密钥传输、使用过程中所面临的安全威胁更为严峻。因此,如何保证在移动端安全地使用密钥进行数字签名[2]成为了目前移动安全应用所面临的关键问题。
目前为了解决常用的1024位RSA算法所面临的严重安全威胁,国家密码管理部门发布了以ECC算法为基础的改进密码算法SM2椭圆曲线公钥密码算法[3]。该方案的正确性、效率和安全性上都优于传统RSA和ECC算法。为了在移动设备上使用基于SM2的数字签名[4],并且符合《电子签名法》私钥只能由合法用户持有并受此用户控制的规定,本文在尚铭等人[5]提出的SM2椭圆曲线门限密码算法和基于多项式的可验证门限密码技术[6]的基础上提出了一种适用于移动终端数字签名系统的可验证SM2椭圆曲线门限密码方案并通过实现该方案,证明本文提出的可验证SM2门限签名系统方案,在增加可接受时间消耗的同时,能抵御移动终端环境下恶意敌手的欺骗攻击以及合谋攻击,更符合移动数字签名的安全需求。
1 相关研究
1.1 SM2数字签名算法
SM2数字签名算法是国家密码安全局于2010年12月17日发布的基于椭圆曲线离散对数问题的数字签名算法。可用于保证身份的真实性、数据完整性和行为的不可否认性等。该算法中由一个签名者对数据产生数字签名,并由一个验证者验证数字签名的可靠性。在使用该算法之前,各参与方需先设定相同的公开参数,包括p、q、E和G,其中p是大素数,E是定义在有限域Fp上的椭圆曲线,G=(xG,yG)是E上q阶的基点。其签名过程如下[5]:
(1)密钥生成阶段,签名者随机选取秘密d,d∈[1,q-1],计算P=dG并将P作为公钥公开,d作为私钥保存。
(2)签名生成阶段,签名者随机选取随机数k∈[1,q-1],计算kG=(x1,y1);随后计算r=(Hash(m)+x1)modq,其中m为待签名的消息,其中Hash(·)是单向哈希函数;若r=0或者r+k=q,则需要重新选取随机数k。最后计算签名值s=(1+d)-1(k-rd)modq,若s=0,也必须重新选择随机数k;否则将(r,s)作为签名结果。
(3)签名验证阶段,验证者接收到m和(r,s)后,首先检查是否满足r,s∈[1,q-1]且r+s≠q;然后计算(x'1,y'1)=sG+(r+s)P;r'=(Hash(m)+x'1)modq,判断r'和r是否相等,若二者相等则签名验证通过,否则验证失败。
1.2 可验证门限密码方案
门限密码方案[6]是指采用秘密分享技术将基本的密码机制生成的结果(密钥或者数字签名等)分布于一定数量的参与者集合中,只有有效的参与者子集进行联合,才能恢复正确的密钥或者发布有效的数字签名,而不合法的参与者子集则无法通过伪造参数恢复出正确的密钥或者产生有效数字签名。门限密码方案需要满足以下两个条件:
(1)每个参与者对密文或者消息应使用自己的子密钥进行解密或签名操作可以得到对应的子明文或者子签名消息,t个子明文或者子签名消息可以恢复出原始明文或者数字签名,而少于t分得子明文或者子签名消息不能恢复出原始数据;
(2)已知子明文或者子签名消息不能获取主密钥与子密钥之间的任何信息。
可验证门限密码方案[6]是在通常的门限密码方案的基础上额外添加验证操作,从而解决不诚实分发者或参与者的问题。在可验证门限密码方案中,分发者不但需要向其他参与者发布自己的秘密份额,还需要广播自己对该秘密份额的证明,当各个成员获取其秘密份额时,需要通过公开的证明对秘密份额的正确性进行验证;在秘密重构阶段,每个参与者也需采用同样的验证方法来对其他成员发布的秘密份额的正确性进行校验。可验证门限密码方案可以抵御以下两种攻击:
(1)恶意的分发者在份额分发协议中向其他参与者发送错误的秘密份额;
(2)恶意的参与者在秘密重构协议中向其他参与者发布错误的秘密份额。
2 改进的可验证SM2门限签名方案
2.1 密钥生成协议
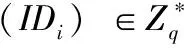
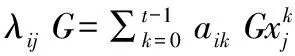


2.2 签名生成协议
(1)参与者集合执行t阶J-RSS和2t阶J-ZSS分享份额分别为βi和αi;
(2)参与者Ui计算并广播γi=βi(1+di)+αi;
(3)参与者Ui记录γj(1≤j≤n),并通过插值公式恢复出γ=β(1+d);

(5)设从参与者集合U中选择2t-1个签名者,设签名者集合为S={i1,i2,…,i2t-1},签名者Ui(i∈S)执行t阶J-RSS,分享份额为ki,并广播Ki=kiG;
(6)签名者Ui执行PM-SS得到kG=(x1,y1),并计算r=(Hash(m)+x1)modq;
(7)签名者Ui计算签名份额si=d'i(ki+r)-r,得到签名s的分享份额si;
(8)至少2t-1个签名者Ui通过广播发布其签名份额si;

(10)签名者Ui通过对接收到的2t-1个正确的签名份额进行插值计算,得到签名结果s=∑i∈Ssi,输出(r,s)作为签名者集合S对消息m的数字签名。
2.3 签名验证协议
(1)签名验证者接收m和(r,s)后;
(2)验证者检查是否满足r,s∈[1,q-1]且r+s≠q;
(3)计算(x'1,y'1)=sG+(r+s)P;r'=(Hash(m)+x'1)modq,判断r'和r是否相等,若二者相等则签名验证通过,否则验证失败。
3 基于可验证SM2移动签名系统的实现
3.1 系统架构设计
基于可验证SM2门限移动数字签名系统结构主要由移动终端客户端、通信服务队列和密钥管理服务器构成,其各自作用如下。
(1)移动终端:移动终端作为客户端,提供客户端软件,支持对客户端密钥的管理,包括:密钥和签名的生成、存储、备份;为提高移动终端应用的安全性,防止java层代码被反编译,从而导致密钥份额等内容泄漏。移动终端应用代码基于Android Studio NDK开发编译生成可安装APK文件,从而增强移动客户端的安全性。
(2)通信服务队列:采用基于AMQP的消息通信服务RabbitMQ,提供分布式消息传递和消息队列服务,利用其高效可靠的消息传递机制为移动终端和密钥管理服务器提供快速稳定的数据交换、份额分发、进程间通信等服务;
(3)密钥管理服务器:配合移动终端设备完成基于SM2的可验证数字签名的生成、保存、备份等操作的服务器。密钥管理服务代码采用C++语言进行开发,其算法执行内容与移动终端执行内容相同。
3.2 功能模块划分
可验证SM2门限签名系统为能够移动终端提供安全可靠的签名服务,根据改进的可验证SM2门限签名方案中的不同协议抽象出不同功能模块,对应分别是:(1)公私密钥生成模块;(2)数字签名模块;(3)数字签名验证模块。各个模块的功能为:公私钥密钥生成模块通过可验证门限密码方案生成移动终端签名群的公私钥;数字签名模块通过可验证门限签名方案生成有效的SM2数字签名;签名验证模块可对数字签名模块生成的SM2数字签名的正确性、有效性进行验证。各个模块相互独立,可以实现移动终端在不同阶段调用的需求。此系统中包含的算法的实现类图如图1所示。

图1 可验证门限分散算法类图
其中:cn_test_JniTest为移动终端应用采用NDK实现的JNI接口声明,包括密钥生成、签名生成和签名验证3个本地接口声明,密钥管理服务端则不包含此函数;base为上述本地接口的对应实现;Participant为基于SM2的可验证门限签名方案的具体实现,包括门限密钥份额生成、验证、重构、数字签名份额生成、验证、重构以及数字签名认证等方法;XSSUtil为Shamir秘密分享的实现,包括随机秘密分享、零秘密分享、乘积秘密分享等过程的实现;ECP为椭圆曲线点类;SM2为SM2密码算法的相关函数,包括SM2密钥生成、SM2数字签名生成、SM2数字签名验证等方法;RabbitMQProp为消息传递服务组件RabbitMQ的基本配置,包括服务端地址、端口等信息、以及对通信队列建立通信连接等方法;queueUtil为消息传递服务组件对消息队列的处理方法,包括消息的收发等操作。
3.3 系统模块设计与实现
3.3.1 密钥生成模块
在本阶段模块的主要工作是产生数字签名系统的公私钥对,主要过程为通过多项式秘密分享的方式分享门限签名密钥份额,并获取通过广播多项式承诺值对密钥份额的有效性进行判断。具体步骤为:
(1)移动终端签名应用发起获取公钥申请,密钥管理服务器获得申请后根据门限值(t,n)创建n-1个密钥服务进程,并初始化数字签名算法涉及的公开参数、创建通信服务队列。
(2)移动终端应用与n-1个密钥管理服务进程同时执行改进SM2可验证门限密码生成协议获得系统公钥以及各自持有的私钥份额。主要函数过程如下:
void getPA(char *x,char *y,char *di, int t,int n,int playerno)
{
randomize();
Participant player=Participant(playerno,t,n);;
mpz_set_ui(init,playerno);
ECP PA;
player.generteKeyShares();
player.collectKeyShares();
player.varifyKeyShares();
player.getPA(&PA);
}
3.3.2 签名生成模块

(1)移动终端签名应用发起数字签名申请,密钥管理服务器获得数字签名申请之后,创建n-1个密钥服务签名进程,并载入对应的私钥份额;

void sign(char *e, char *r,char *s,char *x,char *y,char *di,int t,int n,int playerno,int U[])
{
randomize();
Participant player=Participant(playerno,t,n);
player.shareDi()
}
(3)选取其中(2t-2)个签名进程配合移动终端应用,作为签名参与者执行可验证SM2门限协议5~10步,生成并检验数字签名份额,在获得2t-1个正确的数字签份额后,移动终端应用通过差值公式生产对应的数字签名(r,s),主要函数过程为:
void sign(char *e, char *r,char *s,char *x,char *y,char *di,int t,int n,int playerno,int U[])
{
mpz_t r0,s0,di0,x0,y0;
mpz_init(r0);
mpz_init(s0);
mpz_init(di0);
EC_point PA;
PA.init();
mpz_set_str(PA.x,x,16);
mpz_set_str(PA.y,y,16);
mpz_set_str(di0,di,16);
player.generteSignShares(e0,U);
player.collectSignShares();
player.varifySignShares();
player.get_sign(&e0,&r0,&s0,U);
}
3.3.3 签名验证模块
在此阶段模块中主要实现对签名结果的验证,验证过程由密钥管理服务器执行。具体步骤为:
(1)移动终端应用向密钥管理服务器发起激活签名验证进程请求,密钥管理服务器获取验证请求之后创建签名验证进程,并载入相关参数;
(2)密钥管理服务器签名验证进程检查(r,s)是否满足r,s∈[1,q-1]且r+s≠q;若满足参数条件,则计算基点(x'1,y'1)=sG+(r+s)P以及验证签名值r'=(Hash(m)+x'1)modq,若r'与r是否一致,若二者相等则表明签名没有被篡改,否则签名失效,并将结果返回至移动终端应用。主要函数过程为:
int verify(char *r,char *s,char *e,char *x,char *y)
{
mpz_t r0,s0,e0;;
mpz_init(r0);
mpz_init(s0);
mpz_init(e0);
EC_point PA;
PA.init();
mpz_set_str(PA.x,x,16);
mpz_set_str(PA.y,y,16);
mpz_set_str(r0,r,16);
mpz_set_str(s0,s,16);
mpz_set_str(e0,e,16);
if(SM2.verify(&r0,&s0,&e0,&PA)){
cout<<"签名验证:通过!"< return 1; } else{ cout<<"签名验证:未通过!"< return 0; } } 通常来讲,门限签名的正确性指的是通过签名算法所生成的数字签名结果必须通过对应的签名验证算法,而本文所提出的改进的SM2可验证门限签名方案中涉及密钥份额、子签名份额以及门限签名,下面对这3个结果的正确性进行论证。 定理1:在SM2可验证门限签名方案的密钥生成阶段,参与者Uj能够验证参与者Ui所发送的λij的真伪,从而保证密钥生成阶段产生的参与者各自的私钥份额是正确的。 证明:参与者Ui在密钥生成阶段会公开自己份额对应的校验信息aikG(k=0,1,…,t),λijG可以写成: λijG=fi(IDj)G=ai0G+ai1IDjG+ ai2IDj2G+…+aitIDjtG 根据参与者Ui公开的证明信息,参与者Uj可通过验证上式是否成立来验证参与者Ui所发送的份额参数λij的是否正确,从而保证获取的份额参数是正确的,进而保证参与者Uj通过差值计算获得正确的私钥份额。 定理2:在签名份额生成过程,签名者Uj能够验证合法的签名者Ui所发布的签名份额信息si的真伪,从而保证签名者Uj获取的签名份额是正确的。 siDi(-1)+rDi(-1)-rG= [d'i(ki+r)-r)](d'i)-1G+rDi-1-rG= (ki+r-r(d'i)-1)G+rDi-1-rG=kiG+ rG-rDi-1+rDi-1-rG=kiG 而Ki=kiG,故Ki=siDi-1+rDi-1-rG成立,所以若子签名份额能够通过上式的校验,则证明签名参与者Uj获取Ui签名份额是正确的。 定理3:在数字签名重构过程中,签名者通过差值公式计算得出的签名值s是正确的。 证明:由SM2可验证门限签名生成协议过程第(6)可得r=(Hash(m)+x1)modq,而(x1,y1)=kG式中k=∑i∈Ski,所以x即是点kG的x坐标。由于: (k1+r,…,kt+r)↔k+r, ((1+d1)-1,…(1+dt)-1)↔(1+d)-1, 根据分散秘密重构定理,在获得2t-1个正确的签名份额的条件下: s=∑i∈Ssi=(1+d)-1(k+r)-r,因此该签名方案产生的数字签名是正确的。 在本系统实现方案中通过可验证门限技术保证系统的安全性,以下将从防恶意敌手的欺骗攻击和抗不安全集合的合谋攻击两个方面对该系统方案的系统的安全性能进行论证。 定理1:本文提出的基于SM2的可验证签名方案可以抵御欺骗攻击。 定理2:本文提出的数字签名方案可以抵御合谋攻击。 证明:由Shamir秘密分享方案可知,在(t,n)门限的条件下,大于等于2t-1个成员可以通过合谋重构Lagrange恢复出插值多项式f(x),由于IDi为公开信息,故合谋者可以获得其他群成员Ui的秘密份额λi,但是根据子签名si=(1+di)-1(ki+r)-r,合谋者无法获得Ui的私钥di,因此不能冒充群成员Ui对消息m生成对应子签名份额。所以本文提出的门限签名方案是可以抵抗不安全集合的合谋攻击。 基于第3章的系统设计模型,采用(t,n)门限集合为(2,3)的情况下,在表1所示系统设备上针对可验证SM2门限签名系统方案和普通门限签名方案进行系统运行效率测试,测试结果如图2所示。其中系统参与者由一个移动终端进程和2个密钥服务端进程构成,共同执行改进的可验证SM2门限签名方案和普通签名方案。图2-a,b,c中纵坐标表示分别运行普通门限签名方案和本文提出的SM2可验证门限签名方案在100、200、300、400次运行次数下不同进程在门限签名方案的3个阶段的平均耗时;横坐标A、B、C分别代表使用普通门限数字签名方案的3个阶段,分别为密钥生成阶段、签名生成阶段以及签名验证阶段,而A1、B1、C1分别代表使用可验证SM2门限数字签名方案对应的3个阶段。图2-d则为3个终端分别执行两种方案时各个阶段的总平均时间消耗。 表1 系统设备配置参数 图2 (2,3)条件下两种方案的效率对比 根据图2(a),(b),(c)可以看出在各个终端执行两种方案时的时间消耗与2(d)中的平均结果相差不大,证明本面向移动终端的数字签名系统在良好网络环境下具有良好的稳定性。根据图2(d)中的数据可知在(2,3)条件下,未采用可验证方案的密钥生成阶段平均耗时约40.294 ms,签名生成阶段平均耗时约35.186 ms,签名验证阶段约为4.954 ms;采用可验证方案的密钥生成阶段平均耗时约47.711 ms,签名生成阶段平均耗时约37.687 ms,签名验证阶段约为5.148 ms。由此可以推论采用SM2可验证门限签名方案在增强系统整体安全性和数字签名正确性的基础上同时也增加了一定的时间,但增加的时间消耗在可接受范围。而面对移动终端的开放性环境,对接收的消息做进一步确认是必要的,因此此方案具有一定的实用性和应用价值。 本文提出的基于SM2的可验证门限签名方案,每个参与者私钥由参与者自己选择,并根据可验证秘密分享过程对SM2数字签名进行可验证秘密分享。安全性分析表明在密钥生成、签名生成阶段,利用公开信息进行验证,可以有效避免恶意敌手或者参与者的欺诈,且可以抵御参与者合谋攻击。因此,该方案具有良好的安全性。通过对系统功能的实现以及相关的测试,证实该系统方案的正确性和可靠性。结果证明,基于可验证SM2门限算法的移动终端签名系统满足开放性移动终端安全使用的需求,且相较于同类数字签名方案更贴近实际环境,具有一定的实际应用价值。4 系统分析与讨论
4.1 正确性分析

4.2 安全性分析
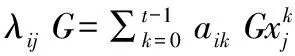

4.3 效率分析


5 结语
