基于EEMD-ICA与SVD的电网谐波检测方法研究
2019-03-19玥,,,珣
玥,, , 珣
(1.西安工程大学 电子信息学院, 西安 710048; 2.三门峡黄河明珠(集团)有限公司,河南 三门峡 472000; 3.西安中冶新材料有限公司, 西安 710061)
0 引言
电能是目前人类社会使用最广泛的能源之一,随着科学技术和国民经济的发展,人们对电能质量的要求越来越高。但伴随着电力电子技术的发展,电网中接入的非线性负载如各种变频变流装置、炼钢电弧炉和电力机车等越来越多,由此而引发的电能质量问题也越来越严重,由于它们具有非线性、冲击性和不平衡的用电特点,会造成电能质量问题,使电网电压波形畸变,引起电压波动与闪变以及含有谐波、间谐波,影响电网及用电设备的安全与经济运行。
目前已有学者采用独立成分分析的盲源分离方法对单通道电网谐波提取进行研究,并取得一定成果。文献[1-2]构造虚拟通道实现单通道电压信号谐波、间谐波分离,得到很好的分离结果。但文中构造虚拟通道需要未知源信号的先验频率信息,并且每分离N个频率谐波,需要构造2N个虚拟通道,算法复杂,不易工程实现。燕山大学孟玲玲[3-4]提出EVD-FastICA和LSM-FastICA算法分离电网谐波,先采用EVD方法确定单通道信号变换成多路观测信号的矩阵阶数,再采用最小二乘法增加谐波检测精度。该方法仍然需要源信号先验频率信息,且具有运算量大等缺点。文献[5-6]分别基于峭度极大的ICA算法和引入相关系数的方法分离电网谐波,但该方法只分离出电网中3、5、7等次数谐波,未提及频率小于50 Hz的电网间谐波的分离,并且待分离源信号并不是单通道情况。文献[7-9]采用SCICA方法[10]通过建立虚拟通道将单通道源信号转换为多通道信号,从而进行ICA分离,并且采用三阶牛顿算法代替二阶牛顿法,使收敛更快,谐波分离效果更好。虽然无需源信号的先验信息,但SCICA只能运用于平稳信号,且不能够分离频率相近的谐波信号。
本文将经验模态分解方法(Empirical-Mode Decomposition, EMD)与独立成分分析方法相结合,分离单通道电网电压谐波、间谐波。不仅无需源信号先验信息,而且对非平稳信号也有很好的分离效果。首先,采用经验模态分解方法,将单通道电压信号进行分解,得到多路本征模态函数分量(Intrinsic Mode Functions, IMF),各IMFs均为每时刻含有单一频率,互相正交且零均值的振荡函数,从而实现单通道信号向多路信号的转换,该转换过程无需任何单通道源信号的先验信息。然后,采用SVD方法对数据进行降维,再运用基于负熵的固定点独立成分分析(FastICA)方法对信号进行谐波、间谐波分离。为了克服经验模态分解(EMD)对噪声高度敏感,鲁棒性差等缺点,本文采用总体经验模态分解(EEMD)代替经验模态分解(EMD)的方法,实现单通道信号到多路信号的转换,降低算法对噪声的高敏感度,增强算法鲁棒性。将EEMD与ICA相结合进行单通道信号分离的方法,已有一些学者进行研究。Bogdan等人[11]首先提出EEMD-ICA方法,提取噪声中的生物信号,如EEG信号,并从仿真和实验两方面与SCICA、WICA方法进行对比,说明了EEMD-ICA方法无需源信号先验信息,分离效果好等优点。国内学者郭一娜,在原有EEMD-ICA算法的基础上,加入PCA算法[12-14],对IMFs进行降维,简化算法,并分离模拟信号对该算法进行验证,取得了很好的效果。ZHANG Chun等人[15]提出SEEMD方法解决了EEMD方法边缘效应问题。Ganesh R等人[16]提出将LDA算法加入到EEMD-ICA中对生物信号EMG特征进行分析。以上的研究均基于对生物信号,如EEG,EMG等的分析与提取。这类信号具有非平稳性大,分离对象频率差别大等特点。含有谐波、间谐波的电网电压信号与上述分析对象(EEG,EMG信号等)相比具有相对平稳,频率差别小等特点。本文首次将EEMD-ICA方法运用到电网电压谐波、间谐波分离问题中,并且采用SVD代替PCA对IMFs数据进行降维,通过模拟信号谐波分离,对所提方法再该领域的应用的可行性进行验证,并且仿真结果进一步说明了该方法与已有的单通道电网电压谐波提取方法相比,更加简洁,准确。
1 算法及原理
1.1 电网电压数学模型
电网电压是频率为50 Hz的正弦波,但由于大量电力电子设备,大功率非线性负载的加入,使电网电压受到污染,产生谐波、间谐波(频率小于50 Hz),受污染的电网电压可表示为:
v(t)=Amsin(ωt+ψ)+Hmsin(n1ωt+φ1)+
Hintermsin(n2ωt+φ2)
(1)
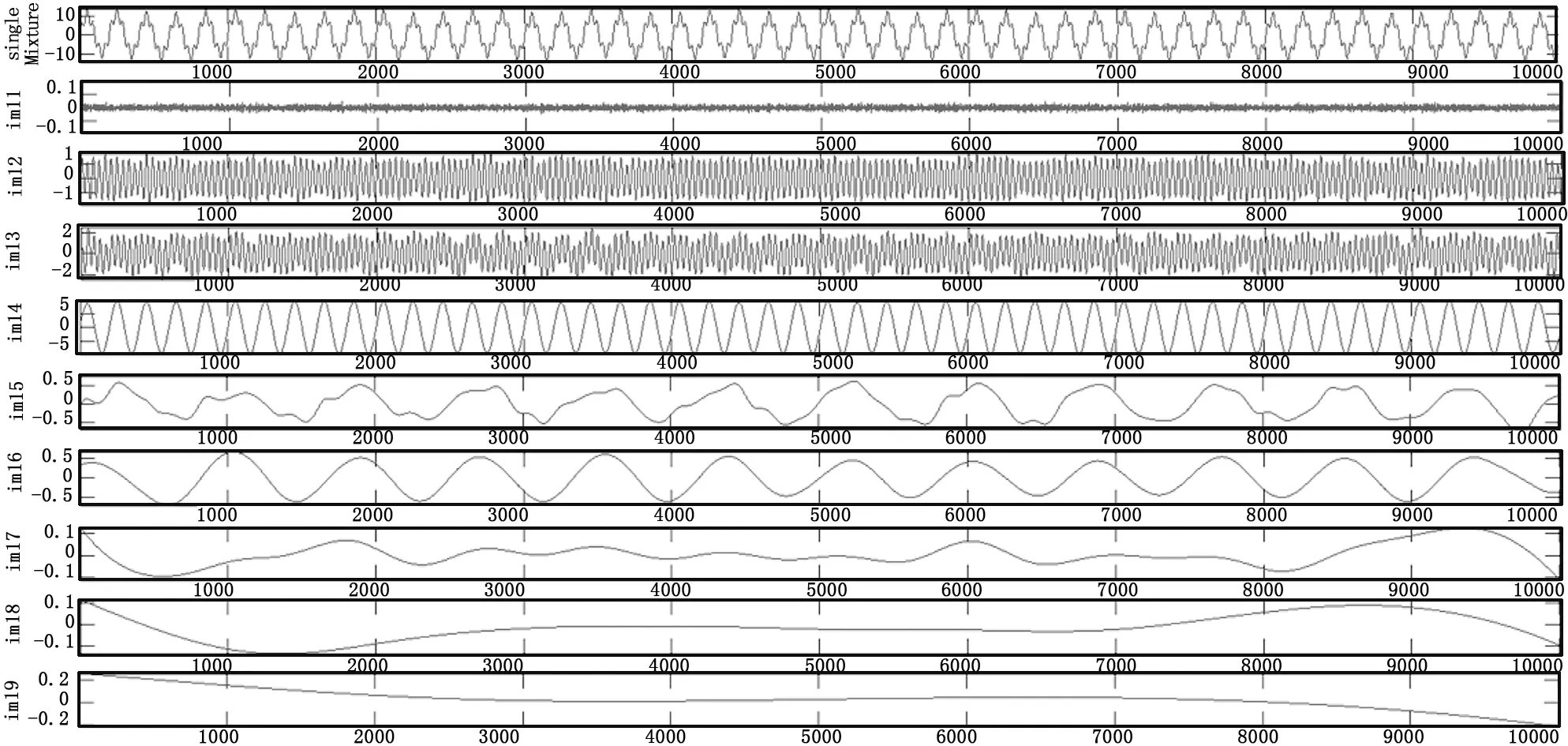
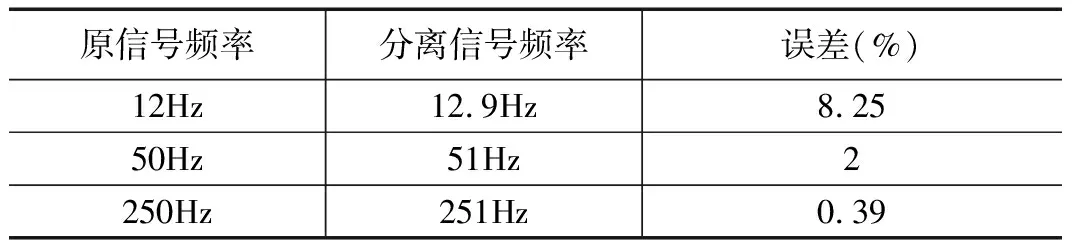
式中,ω=2πf,f=50 Hz,v(t)=Amsin(ωt+ψ)为基波项,Am,ψ分别为基波电压的幅值和初相位;Hmsin(n1ωt+φ1)为谐波项,Hm,φ1分别为谐波电压的幅值和初相位,n1为谐波次数,n1=1,3,5...,2n+1,(为正整数);Hintermsin(n2ωt+φ2)为间谐波项,Hinterm,φ2分别为间谐波电压的幅值和初相位,为间谐波项的频率系数满足0 独立成分分析技术是实现盲源分离的重要方法之一,该方法能够在源信号未知的情况下,通过优化算法将多个观测信号按照统计独立性原则分解为若干独立分量,从而获得源信号的估计量[17]。ICA算法具体描述如下: 设有n个观测信号x1,x2,x3,...,xn,是由个未知源信号s1,s2,s3,.,sm,线性混合而成,每路信号有l个采样值,并且观测信号数量不小于源信号量,即满足n≥m。则有: X=AS (2) 其中X=[x1,x2,…xn]′称为观测信号矩阵,S=[s1,s2,…sn]′称为源信号矩阵,A为混合矩阵,阶数为n*m, 观测信号矩阵X与原信号矩阵S的阶数分别为n*l和m*l。 独立成分分析技术是在源信号S和混合矩阵A均未知的条件下,通过观测信号X估计源信号S及混合矩阵A的过程。假设源信号S中各分量相互独立,且最多只有一个服从高斯分布。通过ICA算法得到分离矩阵W(W=A-1),阶数为m*n,从而得到源信号S的估计量Y: Y=WX (3) 独立成分分析的关键问题是建立分离结果独立性的目标函数及其相应的分离算法。实现ICA的算法有很多,本文采用应用较为广泛,收敛速度快的基于负熵的快速固定点FastICA方法,该方法是由芬兰学者Hyvarinen等人提出。算法框图如图1所示[17]。 图1 FastICA算法框图 经验模态分解(EMD)方法是由Huang N E等人提出[18],可将单通道信号分解为多路本征模态函数分量(Intrinsic Mode Functions, IMF),各IMFs均是互相正交的零均值振荡函数。互相正交保证同一时刻各个IMFs中只含有单一频率,且各个IMFs之间不存在相同频率,该频率称为固有频率。零均值振荡保证各个IMFs存在相同数量的局部极大值和极小值,并且所有极大值均大于0,所有极小值均小于0。 采用EMD方法分解出的多路本证模态函数具有混叠现象,如分离出的两路IMF同一时刻具有相同频率。同时,EMD方法对噪声高度敏感,鲁棒性差。为了克服EMD方法的不足,Huang N E等人对EMD方法进行改进[19],提出总体经验模态分解方法(Ensemble-EMD),该方法通过对单通道信号加入均匀白噪声,降低EMD对噪声的敏感性,增强算法鲁棒性,是一种噪声辅助数据分析方法,同时也是数据驱动型算法。 采用EEMD方法对单通道信号分解,得到多路IMFs分量后,采用FastICA算法对所有IMFs分量进行独立成分分析,得到各独立分量ICs以及分离矩阵W和混合矩阵A。在所有独立分量ICs中寻找与源信号相关性较大的分量,并结合分离矩阵W进行信号重构,实现电压信号谐波分离。 采用EEMD-ICA方法对单通道电压信号进行基波、谐波及间谐波分离,无需任何源信号的先验信息,避免了利用先验信息建立多路虚拟信号,该方法不但能够分离常规谐波(3、5、7次等),对间谐波(频率小于50 Hz)也有很好的分离效果。 采用EEMD将单通道信号转化为多路信号,该过程中由于噪声等因素影响,所得到的IMFs并不都与所要分离的谐波相关,具有高冗余量,因此,在采用ICA对IMFs进行独立成分分析之前需要对数据进行降维。 主成分分析(Principal Component Analysis, PCA)是统计数据、数据压缩以及特征提取中常用的经典方法,目的是将高维空间数据向低维空间投影,消除原高维数据的冗余度,从而实现对原高维数据的降维,其实质是一种用原有变量的线性组合来表示事物的主要方面的分析方法。PCA技术只能够对数据的二阶统计量进行理,常作为ICA中的一个关键的预处理步骤。本节基于式(2)模型阐述PCA的实现方法,PCA算法实现过程如下: (1)将观测矩X中心化(去均值): X=X-E{X} (4) 其中:E{X}为矩阵X的均值,上式中实现矩阵X为零均值矩阵。 (2)求观测矩阵X的协方差矩阵CY: (5) (3)求协方差矩阵CY的特征值与特征向量: CYD=DΛ (6) 其中:D的列向量为CY的特征向量,Λ为对角矩阵,CY其对角元为的特征值λi,i=1,2,…,n。 (4)将特征值λi及其对应的特征向量降序排列,取前k个较大的特征值,将其对应的特征向量作为原高维数据的主成分,并组成新的特征向量矩阵,进行数据重构D',得到降维后的矩阵X'。 X'=(D')TX (7) 上述PCA过程中,通过求协方差矩阵的特征值与特征向量实现主成分分析,实现数据降维。该过程中,对特征值及其特征向量的对角化被球矩阵必须为方阵,即上述过程中的协方差矩阵。协方差矩阵的求取过程的算法复杂度为O(nl),随着原数据的维数的增加,算法的复杂度随之按照2次方的速度增加,大幅度增加系统负担。 为了减化算法复杂度,减少系统运算负担,本文提出采用奇异值分解(SVD)实现主成分分析,对原数据进行降维。具体实现过程如下: (1)将观测矩阵X中心化(去均值): X=X-E{X} (8) 其中:E{X}为矩阵的均值X,上式中实现矩阵X为零均值矩阵。 (2)求新矩阵NX: (9) (3)对新矩阵NX进行奇异值分解(SVD): NX=UCVT (10) 其中:V与U分别为n*n和l*l的方阵,C为有限个非零对角元素的对角矩阵。 (4)将C的对角元素降序排列,取前k个较大的对角值,将其对应的V矩阵的列向量作为原高维数据的主成分,并组成新的特征向量矩阵V',进行数据重构,得到降维后的矩阵X'。 X'=(V')TX (11) 将SVD方法与PCA方法进行对比可以得出,采用这两种方法均可以实现对原始高维数据的降维,但PCA方法需要先求观测信号矩阵的协方差矩阵CY,在求协方差矩阵CY的特征值与特征向量,从而实现主成分分析。本文提出的SVD方法,将观测信号直接进行奇异值分解,得到对角矩阵C与其对应的向量矩阵V,从而得到原数据的主成分。该方法避免了求协方差矩阵的过程,减少了O(nl)的算法复杂度,减少了系统的运算负担,实现了对原高维数据降维算法的优化。因此,本文采用SVD进行数据降维。 为了验证EEMD-SVD-ICA算法对谐波、间谐波分离的有效性,本文采用MATLAB建立基波、谐波以及间谐波线性混合的单通道信号: x(t)=10sin(50*2πt)+3sin(250* 2πt)+sin(12*2πt) (11) 该信号是由频率为50 Hz的基波,250 Hz的5次谐波以及12 Hz的间谐波组成,其波形图如图2所示。 图2 单通道电网电压模拟波形 其中:纵坐标表示信号幅值,横坐标表示采样点个数。图3为模拟信号的FFT频谱图。 图3 模拟信号的FFT频谱图 其中:纵坐标表示频率幅值,横坐标表示频率分布,单位为104πrad/s。由频谱图可以看出,模拟信号中含有12 Hz的间谐波,250 Hz的5次谐波以及50 Hz的基波。 由于ICA算法无法对单通道信号进行分析,因此,运用ICA对信号进行盲源分离之前采用EEMD算法将单通道信号转换为多个彼此正交的本证模态函数(Intrinsic Mode Functions, IMF),再将多路IMF分量运用SVD算法进行降维,最后采用ICA算法进行分离。图4为运用EEMD对图2信号进行分离的各个本征模态函数及原信号波形图。其中,高斯噪声系数为0.2。 图4 运用EEMD分离的各个本征模态函数及原信号波形 将图4中各路IMFs进行ICA分离,得到多路ICA分量。通过与已知信号进行对比,可找出与原信号相关的ICA分量,同时对其进行FFT分析得到频谱分析,如图5所示。 图5 ICA分量及其频谱分析图 表1所示。其中,左侧分别为间谐波、基波以及5次谐波的波形图,右侧分别为其频谱分析图。频谱分析图横坐标表示频率,单位为104πrad/s。分离信号的频率与原信号频率误差如表1所示。 表1 分离信号的频率与原信号频率误差 上一小节中,实现对具有基波、5次谐波以及间谐波的模拟电压信号进行谐波分离,分离结果如图5所示,图中可以证明采用EEMD-SVD-ICA可以将模拟信号中的基波、谐波以及间谐波有效分离,分离出的信号是具有单一频率的波形,并且与原信号相比,频率误差仅为1 Hz左右,如表1所示,即实现了对单通道信号谐波分离,验证了算法的有效性。 采用EEMD-SVD-ICA算法对单通道电压信号进行谐波分离,全过程中无需待分离信号的先验信息,如幅值、频率等,也无需利用上述先验信息建立多路虚拟信号。而是采用EMD方法将单通道信号变换为多路本征模态函数(IMFs)代替多路虚拟信号进行ICA分离。这种方法避免建立多路虚拟信号,并且采用SVD代替PCA方法对多路IMFs进行降维,算法得到大幅度简化。 本文提出基于EEMD-ICA与SVD相结合的单通道电网电压谐波分离方法,基于MATLAB的模拟数据进行谐波提取,仿真结果说明,该方法不仅能够分离出基波和5次谐波,而且对于频率小于50 Hz的谐波也有很好的分离效果。该方法无需源信号的先验信息,并且对非平稳信号也有很好的分离效果,采用SVD代替PCA对数据进行降维,相比于现有的单通道点压谐波分离方法更加简单可靠,为电网电压谐波、间谐波分析,提高电能质量提供了夯实的理论基础。1.2 独立成分分析(Independent Component Analysis, ICA)

1.3 EEMD-ICA算法
1.4 SVD与PCA
2 仿真验证
2.1 仿真结果



2.2 仿真结果分析
3 总结
