基于Kalman滤波器的高精度电子秤设计
2019-03-19,
,
(中北大学 电气与控制工程学院,太原 030051)
0 引言
随着生活节奏的加快,人们对电子产品的要求越来越高。使得很多开发商不得不采用高速处理器来满足人们对于速度的追求。电子称作为日常生活中经常使用的电子产品之一,其显示重量的精度与稳定速度都有待提高。文献[1-3]中采用平均滤波、中值滤波或者去极值滑动平均滤波的方式处理重量数据,但是此类滤波方式不仅会降低系统的动态响应速度[4],而且精确度也有待提高;文献[5]仅采用硬件低通滤波,相对于硬件滤波,软件滤波可靠性高,稳定性好,且不存在阻抗匹配等问题[6]。为此,本设计提出一种Kalman滤波与一阶低通数字滤波相结合的数据滤波方式,不仅提高了系统的动态响应速度,而且使滤波后的数据更加精确。
为了拓展电子称的功能,为用户带来更加贴心、人性化的使用体验,借助STM32高性能、低功耗等优势,本设计集成了日常称重过程中所需要的大部分功能,优化了用户的使用体验。同时电子称与互联网的结合,使得用户可以将消费金额上传到云端,最终可以绘制一条长期的销售额曲线,这对于用户来说非常具有现实意义。
1 电子称的工作原理
该系统以32位微控制器STM32作为主控芯片,外围模块主要包括等强度悬臂梁,应变片组成的惠斯通电桥,A/D转换模块,HMI触摸屏显示模块,OLED显示模块,时钟模块,WiFi通信模块。系统的整体结构图如图1所示。

图1 系统整体结构图
当被称物体放在称盘上时,悬臂梁因受力而产生微小的形变,使得称重传感器输出一对差模电压信号。A/D转换器首先将该信号进行放大,然后转化为数字量供主控芯片使用。主控芯片接着将A/D数值转换为重量,并对该重量数据进行滤波处理,最后显示在触摸屏上;系统利用触摸屏与用户进行交互,数据显示与功能按钮都一起显示在触摸屏上,方便用户操作;OLED负责实时时钟的显示;ESP8266会在用户需要上传数据时自动连接附近可用热点并完成数据上传的任务;电子秤在空闲时能够自动进入睡眠模式,暂停各个功能模块,大大降低了系统的功耗。
2 电子秤的硬件设计
该电子秤的硬件部分主要由称重传感器模块、A/D转换模块、STM32主控模块、显示模块、WIFI通信模块以及时钟模块组成。为了达到国家标准《非自动称通用检定规程JJF 1336-2012》中三级称的标准[7],本设计采用灵敏度为1 mV/V,最大量程为1 kg的称重传感器作为该电子秤的称重传感器,并设计电子秤的分度值为0.1 g,最大量程为500 g。
2.1 称重传感器设计
为了确保四个应变片能够承受到同等强度的应力,设计采用特制的等强度悬臂梁[8],材料选用弹性较大的45号钢材。其形状如图2所示。

图2 等强度梁
在悬臂梁的等强度区域处黏贴有高精度电阻应变片,上下两面各等距离分布两个。然后将电阻应变片接成电桥的形式,这样既可以提高测量精度,也可以防止因温度影响电阻应变片阻值造成的测量误差[9]。电桥原理图如图3所示。

图3 电桥原理图
当悬臂梁受到向下的压力时,上面的应变片将受到拉应力,电阻变大;下面的应变片将受到压应力,电阻减小[10]。假设R1=R2=R3=R4,变化均为ΔR,由电桥分压原理可知:
(1)
(2)
通过上面的推导可以看出,桥臂输出电压与应变片的电阻变化量成正比。图4为0~500 g之间重量与输出A/D值之间的拟合曲线。
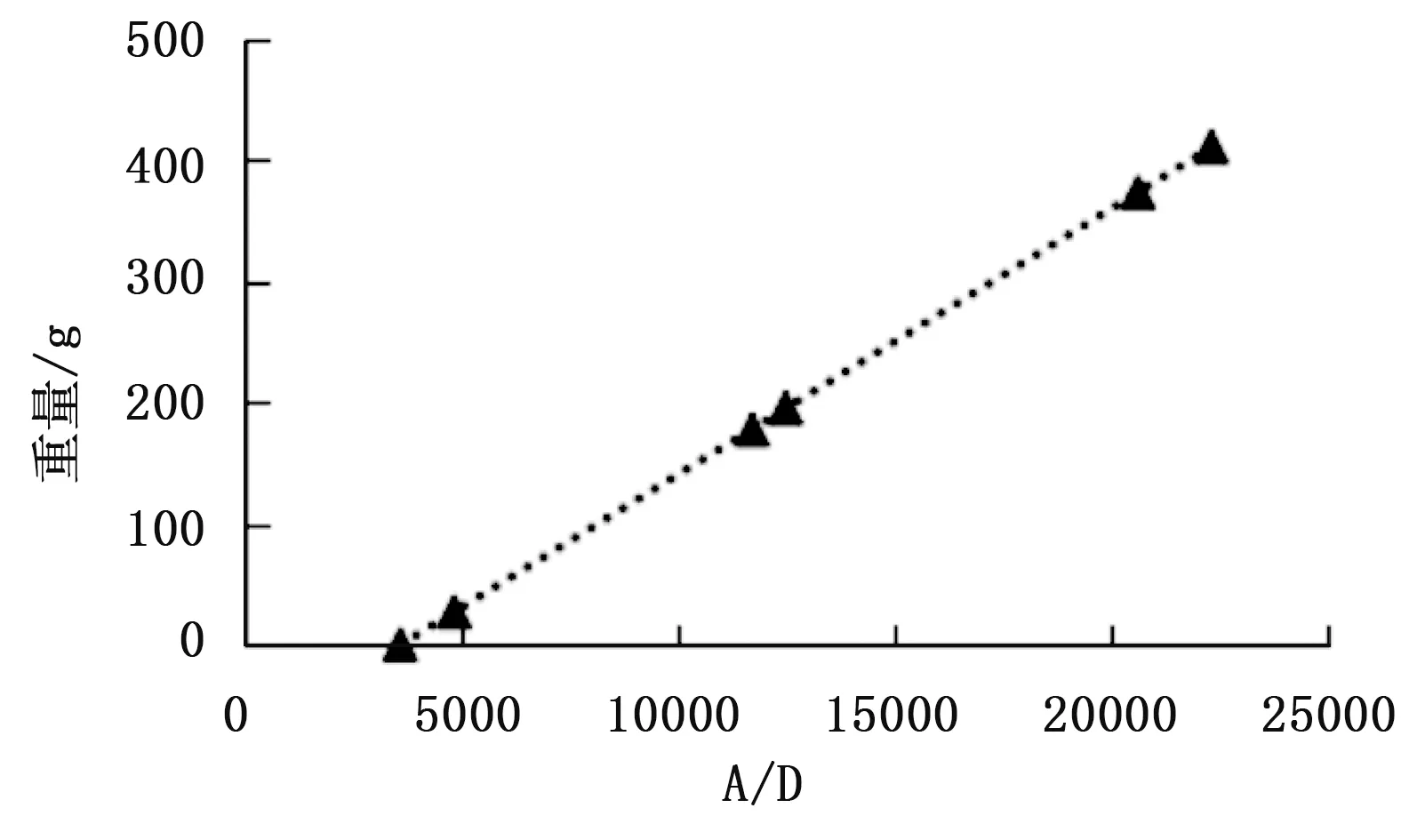
图4 重量、ADC拟合曲线
2.2 A/D转换电路设计
灵敏度与最大量程是电子秤最重要的两个参数[3],由于该电子秤设计的分度值为0.1 g,最大量程为500 g,所以分度数为5 000,考虑到实际中噪声的影响,一般增加裕量后设置为最小分辨率的10倍,故A/D转换电路的分辨率设计为1/50 000。此时A/D转换器至少为16位(16位A/D转换器的分辨率为1/65 536)[1]。本设计采用的芯海科技24位A/D转换芯片CS1237是一款高精度、低功耗的Sigma-Delta模数转换芯片,内置一路ADC,一路差分输入通道和一路温度传感器,完全能满足上述计算的位数要求。图5为A/D转换电路原理图。其中,CS1237采用差分输入方式,参考电压Vref=5.0 V。该芯片内部通过低噪声仪用放大器实现PGA放大,并且可以通过SPI通信接口配置特殊寄存器的方式来选择放大倍数,放大倍数可以设置为1、2、64、128。
设S为称重传感器的灵敏度,Fmax为其最大量程,us为称重传感器的电源电压,Mmin为称重传感器能够分辨的最小载荷量。所以在最小载荷下重传感器的输出umin为:
(3)
其中:S=1 mV/V,Fmax=1 kg,us=5 V Mmin=0.1 g,所以umin=0.5 μV。
采用24位A/D转换器,能够分辨的最小输入电压uin.min为:
(4)
因参考电压Vref=5.0 V,所以uin.min≈0.29 μV。
当称重传感器承受满载负荷时,传感器输出电压umax为:
(5)
因为A/D转换器的最大输入电压uin.max=Vref=5 V,所以信号能够进行的最大放大倍数Amax为:
(6)
综上所述,为了达到高精度的设计要求,选择芯片的最大放大倍数128倍对信号进行放大。

图5 CS1237原理图
2.3 STM32控制模块设计
主控芯片选用以ARM Cortex-M3为内核的STM32系列微控制器STM32C8T6。相对于传统电子秤使用的8位单片机,该芯片CPU时钟频率高达72 M,更加适合处理复杂的计算情况。更重要的是,STM32C8T6具有3种低功耗模式——睡眠、停机和待机。其中在待机模式下,内部电流仅有2 μA。并且可以任意配置低功耗模式下的唤醒方式——中断唤醒或事件唤醒。本设计中,电子称在一定时间内自动进入睡眠模式,其中就包含包含主控芯片的停机模式,大大降低了电量的消耗,达到了节能的目的。
3 电子秤数据滤波器设计
因为A/D芯片在进行数据转换的时候,容易受到各种因素的干扰,包括电源的纹波以及参考电压的浮动等,导致其输出的数据无法很快稳定在一个确定的数值。而传统电子秤的数据处理多采用中值滤波或者去极值滑动平均滤波,但是类滤波算法主要应用于高频震荡系统,虽然滤波后曲线相对光滑,但是会给系统带来很大的延迟,导致其动态响应变慢。而且此类算法在计算时需要占用比较大的系统RAM资源。针对目前存在的滤波精度较低、数据更新不及时和计算复杂度较高等问题,本文设计了一种将Kalman滤波与一阶低通数字滤波相结合的滤波算法。
3.1 Kalman滤波器的算法
随着传感器技术的发展,各种滤波技术也得到了大量的应用和扩展。而Kalman滤波又是目前应用比较广泛的一种滤波技术。下面以线性系统为例,介绍Kalman滤波器的基本理论。
假设线性离散系统方程为:
x(n)=Ax(n-1)+Bu(n)+w(n)
z(n)=H(n)x(n)+v(n)
(7)
式中,x(n)为系统的状态向量,u(n)为输入向量,w(n)为估计噪声向量,A,B为系统矩阵,z(n)为量测向量,H(n)为量测转移矩阵,v(n)为观测噪声向量。其中估计噪声和观测噪声均为符合高斯分布的白噪声,设其协方差矩阵为Q和R。
基于此系统方程,可以推导出线性离散系统方程的最优解。根据系统的预测性,要想估计系统n时刻的值,只需要知道系统n-1时刻态即可:
x(n|n-1)=Ax(n-1|n-1)+Bu(n)
(8)
则系统在n时刻的协方差估计为:
P(n|n-1)=AP(n-1|n-1)AT+Q
(9)
因为由(9)式得到了n时刻的状态预测结果x(n|n-1),而n时刻的系统的测量值为w(n),结合测量值和预测值,可以计算出系统在n时刻的最优估计值x(n|n)。
x(n|n)=Ax(n|n-1)+
K(n)[z(n)-H(n)x(n|n-1)]
(10)
其中:K(n)表示Kalman增益系数:
(11)
在计算出n时刻的最优解x(n|n)的基础上,为了实现下一次的迭代运算,还需要更新一下系统的在n时刻最优解对应的协方差:
P(n|n)=[I-K(n)H(n)]P(n|n-1)
(12)
式中,I为单位矩阵。式(9)~(13)就是线性离散系统的Kalman滤波的基本方程。
由上述分析可以看出,Kalman滤波的工作过程就是不断的预测、矫正。它不需要知道全部过去的数据,而是用前一个估计值和当前的实际测量值来估计信号的当前值,使用起来相对简单,且易于工程实现[11-12]。
3.2 在电子秤数据滤波中的应用
在利用C语言实现Kalman滤波器之前,考虑到该系统为一阶线性系统,故将上述公式中的矩阵向量全部用标量替代,观测值取当前时刻传感器的返回值,系统矩阵A,B取单位矩阵,过程噪声的协方差矩阵Q取0.01倍的单位矩阵,观测噪声协方差矩阵R取单位矩阵。
因为电子秤最小量程为0.1 g,需要显示的重量数据保留两位小数,考虑到绘图精度的问题,下图中纵坐标是对原始的重量数据扩大100倍之后再进行绘制的。图6(a)、(b)分别为电子称在进行称重10 g和20 g重量时的滤波效果图。从图中曲线可以看出,滤波后的重量数据基本保持在0.05 g的误差范围之内。
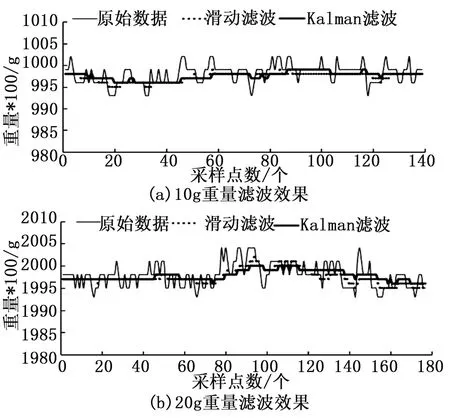
图6 3种滤波算法效果图
考虑到在数据上升阶段,一阶低通数字滤波器的动态响应效果更好,因此设计采用一阶低通数字滤波配合Kalman滤波来实现更好的滤波效果。具体实现思路是当当前采集的数据与上一次滤波后的数据之差大于某一范围时,采用一阶低通数字滤波,这样有利于提高系统的动态响应速度;而当两次数据之差小于这个范围时,采用Kalman滤波,这样有利于提高滤波后数据的准确度。相对于传统的滤波算法,该滤波方式具有响应速度快、数字稳定度高、占用RAM资源小等优势。图7为Kalman滤波搭配一阶低通数字滤波与上述两种滤波算法的动态响应曲线,图中可以看出Kalman滤波与一阶低通数字滤波的动态响应性最好。

图7 3种滤波算法的动态响应曲线
3.3 与原始滤波算法的对比
考虑到衡量算法的主要指标为算法的时间复杂度和空间复杂度[13],为了更深入的分析滤波算法对高精度电子秤的影响效果,下面根据这两个指标来对比分析上述两种滤波算法。
假设x(n)为系统在n时刻的采样值,L为去极值滑动平均滤波器需要的数据个数,则n时刻滤波器的输出x(n)为:

(13)

由上式可知,去极值滑动平均滤波器每接收一个新的采样值,就把该值放在数据内存单元的最后一个数据位置,再将所有数据向前移动一个内存单元,以此覆盖掉第一个内存单元中的数据;然后对这L个数据进行排序,一般采用冒泡排序法;最后在去掉极大值和极小值之后,对中间的L-2个数据计算平均值并作为滤波后的返回值[14]。以后每调用一次这个滤波函数,系统就会按照上述流程执行一次。
故去极值滑动平均滤波在冒泡排序最坏的情况下,该算法的时间复杂度为:
O(L2)+O(log2(L-2))=O(L2)
(14)
空间复杂度为O(1)。
而本设计采用的线性离散系统的Kalman滤波与一阶低通数字滤波算法的时间复杂度和空间复杂度均为O(1)。所以本设计的Kalman滤波与一阶低通数字滤波具有明显优势。
4 实验结果与分析
系统的软件部分采用C语言编程实现,通过在keil上对STM32进行裸机编程,从而实现相应的功能。本系统包含的程序功能函数分为滤波函数,A/D采集函数,重量显示函数,功能选择与切换函数,低功耗判断函数等。图8为系统整体流程图。

图8 系统整体流程图
最后,根据国家最新的电子称检定标准《非自动称通用检定规程JJF 1336-2012》的相关要求,需要利用M1级检定砝码对本文设计的电子称进行偏载误差、线性度误差、重复性误差、鉴别力、零点误差等进行检定。表1为测试结果。

表1 模拟燃料组件测量实验
测试结果表明,随着称重重量的增加,由于等强度梁线性度的微小偏差,使得测量误差呈现增加趋势,但是总体误差始终保持在允许范围内,测量精度达到0.1 g,最大量程达到500 g。因此,根据测试结果,采用Kalman滤波器的高精度电子秤各项指标均达到国家规定的三级称指标。
5 结论
本文设计并实现了基于Kalman滤波器的高精度电子秤称重系统,详细介绍了各个模块的基本原理及实现方案。该电子称的最大量程为500 g,分度值为0.1 g。此类高精度电子称设计的关键在于称重传感器的设计,难点在于其称重数据的处理。由于外部因素的影响,导致电子称显示的数据会出现抖动和漂移。而本设计采用的一阶低通数字滤波配合Kalman滤波很好的解决了这个问题,既提高了电子称的精度,又加快了电子称重量显示的速度。在工厂流水线生产模式中,如果需要称量产品的重量,本设计将节省大量时间。
