基于SLAM的旋翼无人机组合导航算法研究

，， ，

(西北工业大学 自动化学院, 西安 710072)

0 引言

近年来，随着旋翼无人机在军事和民用的领域得到了广泛的应用，旋翼无人机导航算法也得到了深入的研究与探讨。室外环境中，GPS和惯导系统组合导航算法在旋翼无人机组合导航系统中得到了良好的应用[1]，然而在缺乏GPS信号的室内环境或GPS信号受到干扰的情况下，需要其它的辅助或替代方法来实现精确的导航定位[2]。同步定位与地图构建算法(SLAM)指的是搭载特定传感器的主体，在没有环境先验信息的情况下，在运动过程中建立起环境的模型，同时估计自己的运动[3]。因此，可以在组合导航系统引入SLAM算法实现在GPS信号缺失情况下的精确导航定位[4]。

SLAM起源于1986年在旧金山举行的IEEE机器人与自动化会议，大多SLAM工作以激光雷达作为主要传感器。SLAM算法在陆地、室内和水下载体中的应用已经取得很大的进展，将其应用于旋翼无人机是组合导航领域的一个新的研究方向[5]。惯性/SLAM导航系统应用组合导航思想，将SLAM输出的位置姿态估计与惯性测量单元(IMU)的测量相融合[6]，获得全状态估计，它不仅能够达到较高的定位精度，导航参数的输出频率也得到统一。基于上述惯性/SLAM组合导航的特点，本文提出一种基于SLAM的组合导航算法，该算法首先利用扫描匹配的方法，将当前帧与地图之间的关系作为一个优化问题寻找全局最优解，然后采用组合导航算法融合惯性元件和扫描匹配算法输出的导航参数，获得精确的导航信息。最后通过仿真实验验证所设计组合导航系统稳定性和有效性。

1 系统构成

本文研究对象是旋翼无人机组合导航系统，该系统的主要组成有嵌入式计算机、惯性测量单元(加速度计、陀螺仪)、磁力计、单点测距激光雷达和二维激光雷达等，图1是实验平台的实物图。平台选用SLAMTEC公司的Rplidar A2激光雷达，它可以实现对周围环境的360度全方位扫描测距检测，从而获得周围环境的轮廓图[7]。考虑到测量精度和成本，选用单点测距激光雷达TF mini作为高度计，TF mini基于ToF原理，可以实现稳定的距离测量。

图1 搭载激光雷达的实验平台

惯性测量单元和导航计算机构成捷联惯导系统，捷联惯导系统可以输出无人机姿态信息和位置信息。磁力计可以解算出姿态角信息。激光雷达数据经过扫描匹配后可以获得旋翼无人机的位置信息，通过联邦卡尔曼滤波的方法对捷联惯导系统和激光雷达的数据进行融合，更新无人机状态，获得无人机精确的位姿估计。系统原理图如图2所示。

图2 系统原理图

2 基于扫描匹配的SLAM算法

帧到地图全局扫描匹配算法是一种相对定位过程[8]，假设一个旋翼无人机在平面上从位置x0移动到x1，在位置x0和x1，它会分别接受到激光雷达扫描到的点云S0和S1。扫描匹配的过程就是找到一个刚体转换ξ，使得t时刻点云St能与t-1时刻点云St-1匹配。只考虑二维平面情况下，可以用ξ=(px,py,ψ)T表示旋翼无人机的位置平移量和航向角。

高斯-牛顿迭代算法可以用于求解一个最优值，该方法最早出现在计算机视觉研究中[9]，它是以梯度下降法为基础的算法。梯度下降法又称最速下降法[10]，这种算法计算量小，能迅速找到最优解，因此在很多大规模数据集的处理上都会运用到梯度下降法或其改进算法。

考虑激光雷达工作的二维平面，高斯-牛顿方法的基本思想是通过多次迭代，寻找出一个最优解ξ=(px,py,ψ)T，使得对应的这帧的激光雷达点云在栅格地图上表示的概率值的残差之和ξ*最小，其中ξ*表示为：

(1)

这里Si(ξ)是激光扫描点集si=(si,x,si,y)T，它们都是ξ的函数。n为一帧激光雷达点云中点的总个数。将激光雷达扫描点的全部坐标si=(si,x,si,y)T转换到导航坐标系坐标Si(ξ)，激光扫描点集在在导航坐标系下位姿由下式表示：

(2)

Si(ξ)对应的位姿在栅格地图中的映射的概率值可以表示为M(Si(ξ))，接下来开始求解最优迭代步长Δξ，求解公式如下：

(3)

首先将函数M(Si(ξ+Δξ))进行一阶泰勒展开：

(4)

其次，要求出Δξ取何值使函数(4)的值最小，需要对Δξ求导并且令导数等于 0，即：

(5)

根据公式(5)求解Δξ的的过程，引入高斯牛顿方程求解最优步长：

(6)

式中,

(7)

H叫Hessian矩阵，对公式(2)求导可得到：

(8)

在栅格地图中应用双线性插值算法，地图梯度▽M(Si(ξ))可以表示为：

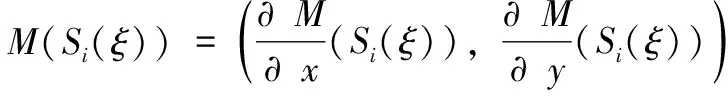
(9)

已知▽M(Si(ξ))和∂Si(ξ)/∂ξ，则可以估计高斯牛顿迭代的最优步长Δξ。累加获得的最优步长Δξ，从而可以得到旋翼无人机在以起始点为原点的北东地导航坐标系中的二维位置。

通过基于扫描匹配SLAM算法可以对旋翼无人机二维位置进行更新，同时，由单点测距激光雷达构成的高度计可以对旋翼无人机的高度进行更新，因此，由激光雷达和高度计组成的SLAM组件实现了对旋翼无人机三维位置估计。

3 组合导航算法设计

为了提高多旋翼无人机导航定位的精度和可靠性，本节应用组合导航理论设计导航系统，在上节得到SLAM组件输出的位置信息的基础上，融合捷联惯导系统输出信息，设计基于联邦滤波组合导航算法。

捷联惯导系统模型中，将姿态误差角、位置误差、速度误差、陀螺仪以及加速度计测量误差作为状态量[11]，得到捷联惯导系统的误差模型[12]。针对旋翼无人机自身特点与应用环境，采用简化的捷联惯导系统误差模型进行卡尔曼滤波算法的设计，简化后的捷联惯导系统模型如公式(10)所示。

(10)

将惯性传感器测量误差模型从捷联惯导系统的误差模型中提取出来，它的数学表达式为：

(11)

通过上式可以看出，可以通过一个单独设计的卡尔曼滤波器对姿态角误差和陀螺仪误差进行估计。本节使用加速度计、陀螺仪和磁力计组成一个联邦滤波子系统，将该子系统称为子滤波器1，用来对姿态角误差和陀螺仪测量误差进行估计。

在子滤波器1中，只有对姿态角误差和陀螺仪误差的观测量，所以子滤波器1估计的状态量也只包含姿态角误差和陀螺仪误差，这样可以有效降低状态维数，提高运算速度。

SLAM组件、陀螺仪和加速度计组成联邦滤波器的另一个滤波子系统，将该子系统称为子滤波器2，公式(10)通过子滤波器2进行状态量的估计。分别通过子滤波器1和子滤波器2对捷联惯导系统的误差进行估计，大大提高了组合导航算法的精度。

综上，本节所采用的的联邦滤波器结构设计如图3所示。

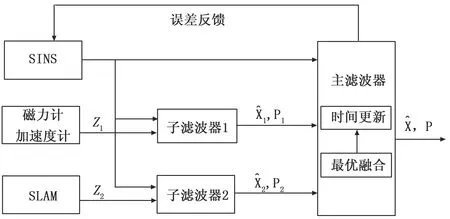
图3 联邦滤波器结构设计图

子滤波器1包含加速度计、陀螺仪以及磁力计3种传感器。卡尔曼滤波器1的量测量为加速度计、磁力计解算的姿态角和组合导航算法给出的当前时刻姿态角的差值。子滤波器1结构如图4所示。

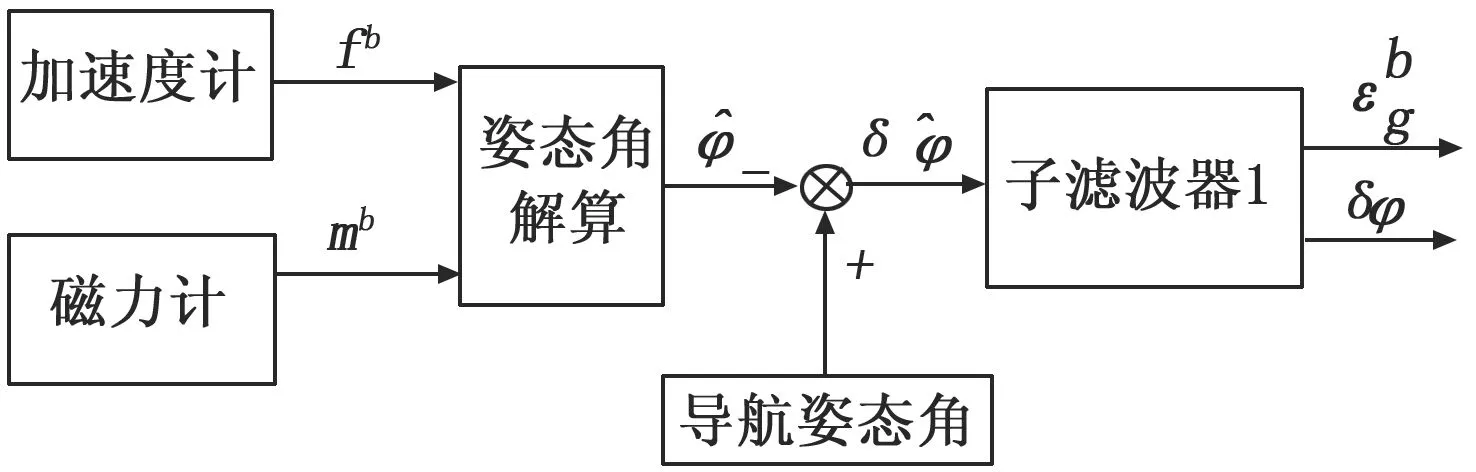
图4 子滤波器1结构图

子滤波器1中，选取包含姿态角误差和陀螺仪误差的六维向量作为状态方程的状态量。状态方程为:

(12)

根据加速度计和磁力计解算旋翼无人机姿态角方法，将组合导航算法输出姿态角与传感器解算姿态角之差作为子滤波器1的量测量。则子滤波器1的量测方程有如下形式：

(13)

子滤波器2包含陀螺仪、加速度计以及SLAM组件。首先利用SLAM组件获得导航坐标系中的位置信息，子滤波器2以SLAM组件输出的位置与导航算法给出的当前位置的差值作为位置误差的量测信息。子滤波器2结构如图5所示。

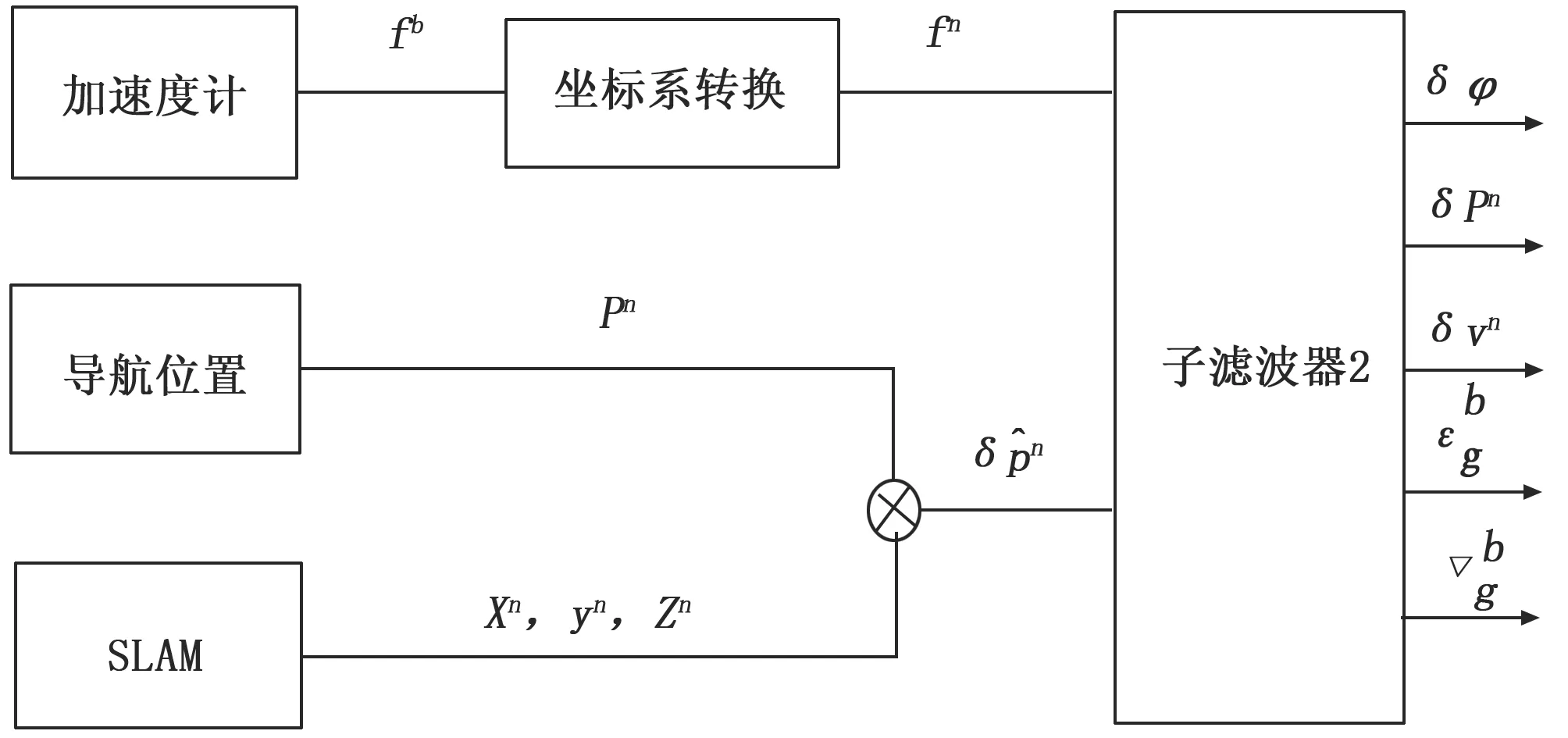
图5 滤波子系统2结构图

子滤波器2中，选取选取姿态误差角、位置误差、速度误差、陀螺仪以及加速度计测量误差共15维的变量作为卡尔曼滤波器状态量。根据公式(10)，子滤波器2状态方程可以表示为：

(14)

由于子滤波器2使用SLAM组件输出的位置信息与组合导航算法给出的位置之差作为子滤波器2的量测量，而且SLAM组件给出的数据本身就是离散形式，因此子滤波器2的量测方程可以直接用离散化的形式表示：

(15)

(16)

主滤波器对两个子滤波器中的公共状态量进行融合，比较两个滤波子系统的状态变量可知，两个子滤波器的公共状态为：

(17)

本文中联邦滤波器公共状态融合算法如下：

(18)

由于子滤波器2中的独有状态可以直接作为主滤波器的状态量输出，因此主滤波器输出的状态量为：

(19)

公式(18)和公式(19)中的下标[a,b]表示只取相应量对应部分的值。

同时，需要将主滤波器状态量中的陀螺仪误差和加速度计误差部分反馈到惯性导航系统中，作为导航系统的更新中的一部分，从而减小导航参数更新时的误差。

4 仿真实验分析

4.1 实验数据的采集

利用图1所示的实验平台，使飞控组件和SLAM组件同时采集陀螺仪、加速度计和磁力计输出信息和SLAM组件输出的位置和高度信息，将采集到的数据通过MATLAB对所设计的联邦滤波算法进行仿真验证。

数据采集环境为西北工业大学自动化学院楼走廊，实验环境如图6所示，图中线为遥控的实验平台运动路线，白色圆圈处为起点位置，深色圆圈处为终点位置。

图6 数据采集环境

基于扫描匹配的SLAM算法在嵌入计算机TK1上实时输出旋翼无人机的二维位置，高度信息由TF mini直接输出并存储。二维位置数据记录在.rosbag文件中，通过在PC平台上对rosbag文件进行回放，将/pose输出位置信息生成位置信息文件，在MALTAB中绘制建图过程中实验平台轨迹图如图7，图中坐标系为以起点处位置为原点的北东地导航坐标系。

图7 实验平台运动轨迹

观察图7中的实验平台轨迹，实验平台位置的估计轨迹同遥控给出的运动指令基本一致，只是局部由于实验平台运动过程中的抖动出现了位置的畸变，说明通过基于扫描匹配的SLAM算法能够实现有效的同步定位与室内建图。

4.2 仿真结果与分析

4.2.1 姿态角滤波结果分析

根据图8可以看出，使用基于联邦滤波组合导航算法之后，姿态角被钳制在一个很小的范围内，有效抑制了姿态角的发散，为速度和位置的解算提供了保障。

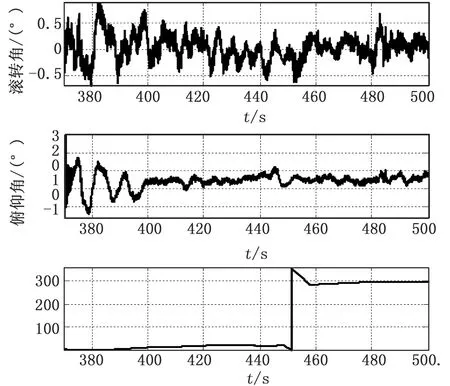
图8 联邦滤波器解算姿态角

4.2.2 速度滤波结果分析

观察图9，使用基于联邦滤波组合导航算法之后，北向速度首先稳定在0.2 m/s左右,442 s以后北向速度回归到0值左右。东向速度首先在0值左右浮动，442 s后逐渐在[-0.1,-0.2]区间变化，地向速度由于采样设备抖动，其值在[-0.4,0.4]区间变化。三个方向的速度变化趋势基本同采样时无人机运动先北向运动后西向运动的运动趋势相吻合。

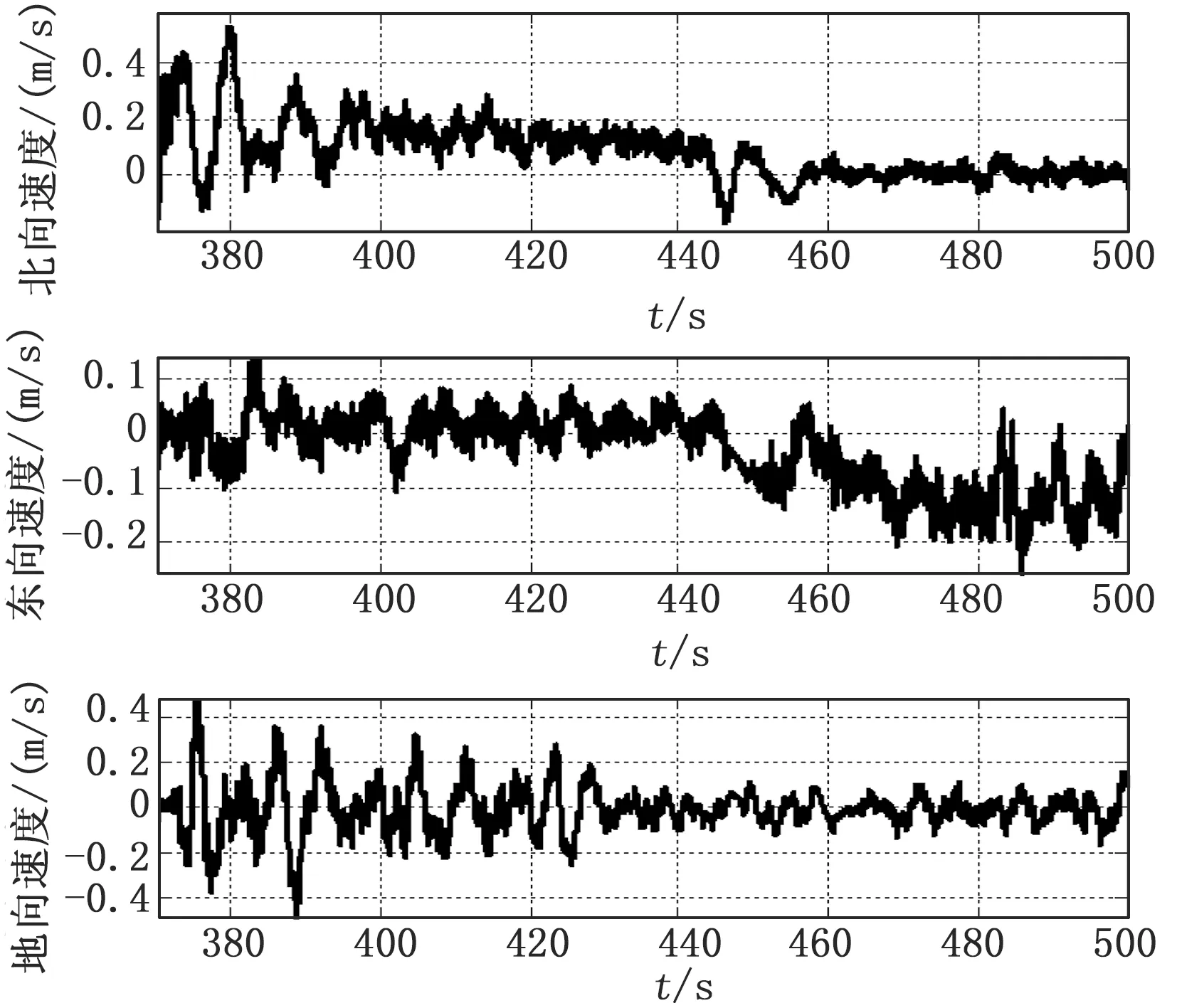
图9 联邦滤波器解算速度

4.2.3 位置滤波结果分析

对比图10中的联邦滤波器曲线和SLAM组件曲线可以看出，位置数据整体比较接近，SLAM输出数据噪声较大，经测量北向和东向位置误差值可达50 mm，经过联邦滤波器滤波有效滤除噪声，滤波后北向和东向位置噪声值不超过20 mm，提高了导航数据的精度。受采样设备抖动的影响，SLAM组件输出的地向位置抖动幅度较大，联邦滤波器能够有效跟踪地向位置的变化，经测量滤波后地向位置误差在40 mm以内，能够满足旋翼无人机室内导航的需求。

图10 联邦滤波器解算位置

5 结论

本研究针对旋翼无人机组合导航系统，引入基于扫描匹配的SLAM算法，提出一种基于SLAM的旋翼无人机组合导航算法。通过仿真实验，将组合导航算法与单独的SLAM算法进行对比，实验结果表明了基于SLAM的组合导航算法的可行性与优越性，为旋翼无人机在未知环境中的自主飞行提供了更精确的定位方法。以后将在论文基础上，继续研究旋翼无人机的自主导航工作。