一种球形滚动机器人的路径跟踪控制器设计

，， ，

(1.辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001；2.北京邮电大学 自动化学院，北京 100876； 3.北京印刷学院 信息工程学院，北京 102600)

0 引言

球形滚动机器人是近些年发展起来的一种新型移动机器人，此类移动机器人采用内部驱动单元实现外部球壳滚动。球形滚动机器人具有完全封闭、滚动灵活、抗倾翻和耗能低等特性，这些特性使此类移动机器人对外界环境表现出很强的适应力，因而逐渐受到国内外学者的关注[1-11]。球形滚动机器人是一种内驱动式非完整滚动球体，点接触式滚动形式虽然减小了球形滚动机器人的运动阻力，但也增大了球形滚动机器人的控制难度。因此，球形滚动机器人的控制问题逐渐成为球形机器人领域的研究热点之一。

球形滚动机器人的跟踪控制问题一般包括球形滚动机器人的轨迹跟踪控制问题和球形滚动机器人的路径跟踪控制问题。与轨迹跟踪控制[11]相比，路径跟踪控制[1-8]仅要求球形滚动机器人的运动路径与参考几何路径一致，而不要求球形滚动机器人于指定时刻到达指定位置。文献[1-3]提出了基于曲率控制的球形滚动机器人路径跟踪控制方法，通过调节球形滚动机器人的横向姿态和纵向速度来实现球形滚动机器人对于期望路径的渐近跟踪。文献[4]提出了一种基于相对曲率半径控制的球形滚动机器人路径跟踪控制方法，通过改变球形滚动机器人的滚动轴水平倾角来实现球形滚动机器人对于参考路径的跟踪控制。文献[5]提出了一种基于运动学模型和动力学模型分析的球形滚动机器人路径跟踪控制策略，并基于所提出的控制策略分别设计了PD控制器和自适应滑模控制器。文献[6]提出了一种基于模糊分级滑模控制的球形滚动机器人路径跟踪控制方法，所提出的控制方法能够实现球形滚动机器人稳定的路径跟踪。文献[7]基于滑模控制设计了一种球形滚动机器人的路径跟踪控制器，实现了球形滚动机器人对于倾斜平面上参考路径的渐近跟踪。文献[8]提出了一种基于神经网络补偿的模糊控制方法，实现了球形机器人系统对于滚动平面上期望路径的跟踪控制。综上可见，目前对于球形滚动机器人路径跟踪控制问题的研究相对较少，已取得的研究成果还处于理论探索和初步实验阶段，相关的理论与方法仍然有待于进一步完善和探索。

在建立一种球形滚动机器人运动模型的基础上，本文设计了一种基于自适应滑模控制策略的路径跟踪控制器。首先推导球壳纯滚动和无自转非完整约束条件下球形滚动机器人的运动方程，然后在此基础上设计一种滑模增益自适应控制器，该自适应滑模控制器能够保证球形滚动机器人的运动路径收敛于期望的参考路径，最后通过数值仿真与样机实验验证本文设计的路径跟踪控制器的有效性和理论分析结果的正确性。

1 球形滚动机器人的运动方程

BYQ-III型球形滚动机器人[9-10]是一种配重驱动式球形滚动机器人，该球形滚动机器人的基本结构如图1所示。BYQ-III型球形滚动机器人主要由球壳1、框架2和配重5三个部分构成，该球形滚动机器人内部配置了两台独立的驱动电机，分别为框架电机3和配重电机4。框架电机3和配重电机4的旋转轴通过球壳中心并且相互垂直，在两台驱动电机的作用下配重5在球壳1内可以进行横向和纵向的摆动。配重5的摆动使该球形滚动机器人的重心偏移，从而实现该球形滚动机器人在地面上的横向运动和纵向运动。

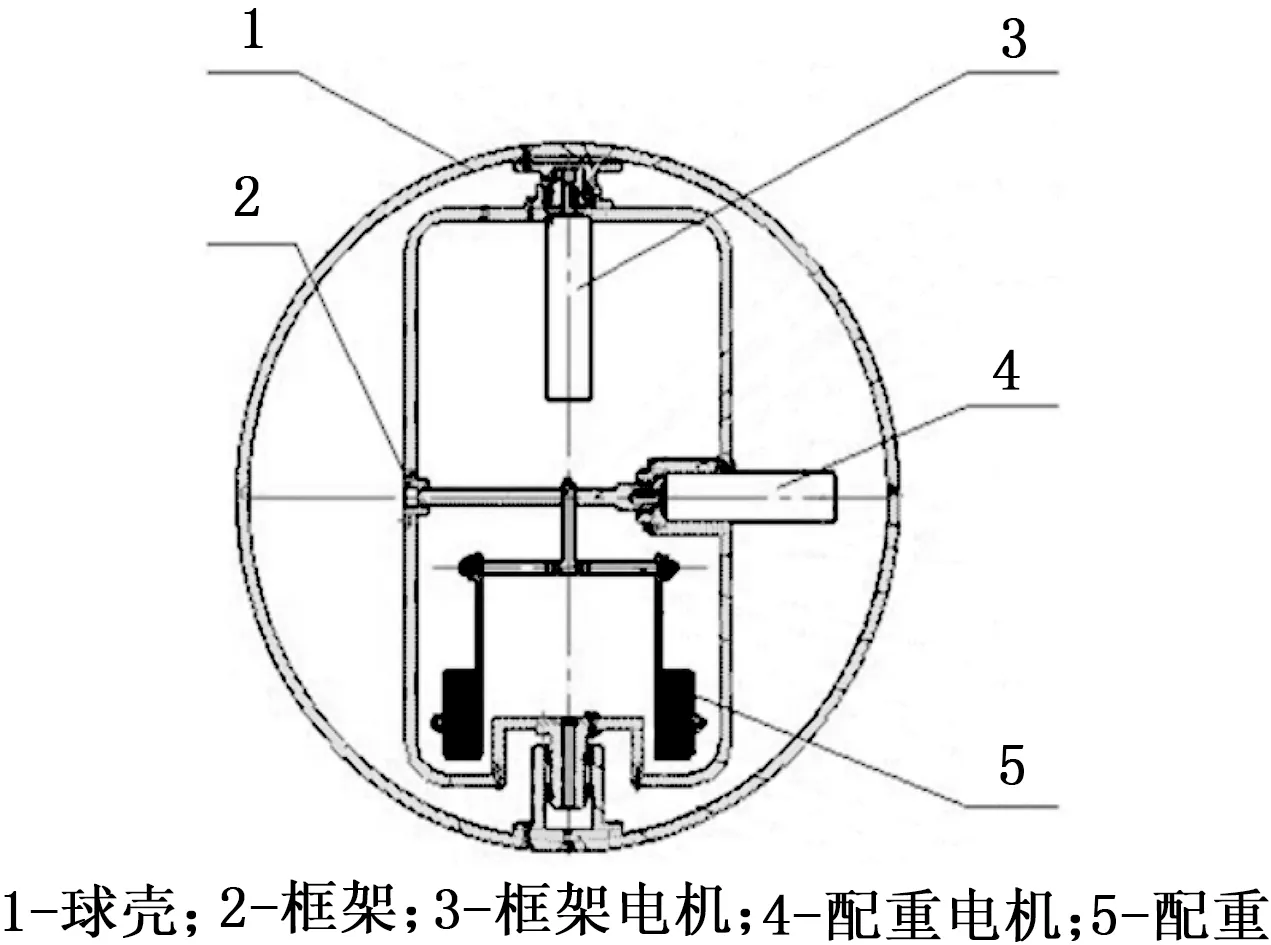
图1 BYQ-III型球形滚动机器人的基本结构

球形滚动机器人的运动模型是分析球形机器人系统的运动学特性和动力学特性的重要基础，也是有效实现球形滚动机器人稳定运动控制的前提条件。因此，为建立有效的控制方法以实现BYQ-III型球形滚动机器人准确的路径跟踪，需要首先建立该球形滚动机器人的运动模型。

在推导BYQ-III型球形滚动机器人的运动方程之前，首先对该球形机器人系统作出如下合理性假设。

假设1：BYQ-III型球形滚动机器人的外壳为均质对称的薄壁球壳，并且该球形滚动机器人在地面上运动时球壳纯滚动且无自转[5-8, 11]。

图2 具有2个输入的均质薄壁球壳模型

当BYQ-III型球形滚动机器人在地面上滚动时，若忽略球壳与内部驱动单元的耦合动力学特性，则该球形机器人系统可以等效为如图2所示的具有2个输入的均质薄壁球壳。ΣO{X,Y,Z}为固连于地面的惯性坐标系，ΣC{X1,Y1,Z1}为固连于球壳的运动坐标系，ΣC的坐标原点位于球壳中心C。由惯性坐标系ΣO到运动坐标系ΣC的Z-Y-X欧拉角分别为航向角φ、横滚角θ和俯仰角φ。τφ和τθ分别为框架电机的输出力矩和配重电机的输出力矩。由于球形外壳具有全向对称性，球壳与XOY平面的接触点P和球壳中心C的运动路径完全一致。设球壳与地面的接触点P在XOY平面内的惯性坐标为(x,y)，球壳的半径为r，球壳的质量为m，球壳的转动惯量为I。

该球形滚动机器人纯滚动和无自转的非完整约束可以表示为[5-8, 11]：

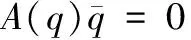
(1)

式中，广义坐标向量q和约束矩阵A(q)分别为：

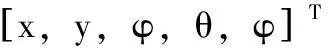
(2)

(3)

分别计算该球形滚动机器人的动能K和势能P，可得该球形机器人系统的拉格朗日函数L为：

L=Κ-P=

(4)

利用含约束乘子的拉格朗日方程，可得该球形滚动机器人的动力学模型为：

(5)

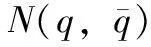
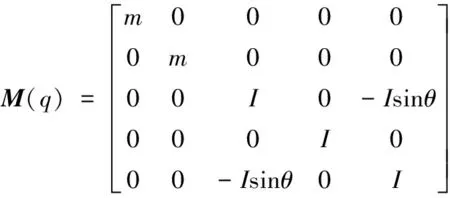
定义矩阵C(q)为:

(6)

式中，

由约束条件式(1)，可得该球形机器人系统的运动学模型为：

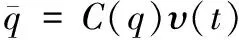
(7)

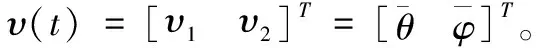
(8)

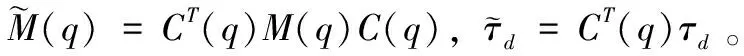
引入新的控制输入u为:

(9)

将式(9)代入式(8)，可得该球形机器人系统的简化动力学模型为:

(10)

至此，该球形机器人系统的运动方程可以表示为：

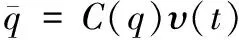
(11)

2 路径跟踪控制器设计

2.1 滑模自适应增益控制律设计

对于球形滚动机器人，其路径跟踪的控制目的是实现球壳与地面的接触点P对于地面上参考几何路径的准确跟踪。

设地面上给定的参考几何路径为：

f(x,y)=0

(12)

这里，假设参考路径的描述函数f(x,y)足够光滑，光滑函数f(x,y)存在关于x和y的二阶偏导数。

定义球形机器人系统的路径跟踪误差为：

ep=f(x,y)

(13)

至此，式(11)所示的球形机器人系统的路径跟踪的控制目标转化为选取适当的控制律u，使式(13)所示的球形滚动机器人的路径跟踪误差ep收敛至零。

基于球形机器人系统路径跟踪控制的上述目标，分别设计机器人系统的滑动变量s1和s2为：

s2=υ2-c2

(14)

式中，c1和c2为正常数。

由式(13)和式(11)，可以得到:

(15)

式中，

对式(15)求导，进一步可得:

(16)

式中，d1=J1(q)C(q)ud。

由式(7)和式(11)，可以得到:

(17)

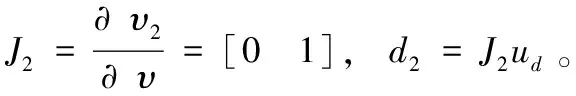
对式(14)求导，由式(15)至式(17)可得：

(18)

式中，

由式(6)、式(15)和式(17)，可以得到：

B=

(19)

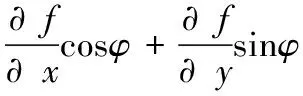
u=B-1ν-B-1G

(20)

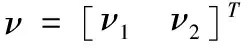
将式(20)代入式(18)，可以得到：

(21)

(22)

在式(21)基础上，设计滑模自适应增益控制器为：

ν=-α(t)sign(S)-βS

(23)

式中，

式中，β1和β2为正常数；切换增益αi(t)如下所示：

(24)

式中，γi>0，αi(0)>0；εi、σi和μi为很小的正常数。在式(24)中，引入参数σi和μi的目的只是为了保证控制器的切换增益αi(t)>0。为求清晰起见，在本文后面的分析和讨论中不失一般性地假设：对于任意时刻t，均有αi(t)>σi。

对于本文设计的路径跟踪控制器式(23)，这里进一步作出如下几点说明：

(1) 路径跟踪控制只要求式(13)所示的路径跟踪误差ep收敛至零，即仅需保证式(14)中滑动变量s1的收敛性。由此可以看出，式(14)中滑动变量s2的设计并不唯一。一般而言，可以选取式(7)所示的准速度υ1或υ2作为被控量来设计机器人系统的滑动变量s2，从而使式(18)所示的矩阵G和B具有相对简单的形式。对于式(14)中滑动变量s2，其中的正常数c2的取值与稳态时球形滚动机器人的运动速度有关。由式(7)不难看出，正常数c2的取值越大，机器人系统进入滑动模态后球壳的滚动速度就越快。

(2) 由式(23)和式(24)可以看出，本文设计的滑模控制律实际上由变速趋近项-αi(t)sign(si)和指数趋近项-βisi两部分构成。在本文控制律式(23)中，变速趋近项能够根据滑动变量si的变化自适应地调节控制器的切换增益αi(t)。当|si|>εi时，切换增益αi(t)逐渐增大使其足以压制扰动和不确定项di。当si减小至|si|<εi时，切换增益αi(t)逐渐减小，以减轻滑模控制器的抖振现象。与文献[12]方法相比，本文方法在控制律式(23)中进一步加入了指数趋近项-βisi，指数趋近项-βisi能够动态地适应滑动变量si的变化，可使滑动变量si更快地收敛至零。系统状态越远离滑动面si=0，指数趋近项的控制作用就越强。

(3) 受建模误差和外部干扰等不确定性的不良影响，实际机器人系统无法产生理想的滑动模态si=0，只能在较小的零邻域内建立真实的滑动模态。对于本文设计的自适应滑模控制器式(23)，滑动变量si能够在有限时间内收敛至零邻域|si|<εi，并在此后始终保持在一个更大的收敛域|si|<δi内，即机器人系统的真实滑动模态在零邻域|si|<δi内存在。该零邻域收敛半径δi的具体表达式如式(25)所示，收敛半径δi的大小可以通过调节参数γi来进行控制，正常数γi取值越大，收敛半径δi越小。

(25)

2.2 稳定性分析

定理1：对于式(11)所示的球形机器人系统，按式(14)设计机器人系统的滑动变量s1和s2，若采用式(20)和式(23)所示的输入变换和控制输入ν，则机器人系统的滑动变量s1和s2能在有限时间内收敛至|si|<δi。

证明：首先，证明控制器的切换增益αi(t)是有界的。

关于控制器的切换增益的有界性，本文此处只进行定性的说明，更为详细的分析请参阅文献[12]。

不妨设初始时刻为t0，并且当t=t0时|si(t0)|>εi。由切换增益的自适应律式(24)可知，从初始时刻t0开始切换增益αi(t)逐渐增大。又由扰动和不确定项di的有界性可知，必然存在某时刻t1，当t=t1时切换增益足以克服扰动和不确定项di，并使滑动变量si(t)从t1时刻开始逐渐减小。设当t=t2时，滑动变量si(t)已减小至|si(t2)|<εi。由切换增益的自适应律式(24)可知，从t2时刻开始切换增益αi(t)逐渐减小，并且当t=t2时切换增益达到最大值αi(t2)。由于切换增益αi(t)不断减小，因此必然存在某时刻t3，当t=t3时切换增益已不足以压制扰动和不确定项di，于是滑动变量si(t)从t3时刻开始逐渐增大。设当t=t4时滑动变量si(t)已增大至|si(t4)|>εi，于是上述过程又从头开始不断重复、循环。

∀t>0

(26)

然后，分别对|si|>εi和|si|<εi两种情况进行分析。

(1) 对于|si|>εi的情况，这里采用Lyapunov稳定性理论证明滑动变量si能够在有限时间内收敛至|si|<εi。定义Lyapunov函数Li(t)为：

(27)

式中，ξi为小于γi的正常数。

对式(27)求导，由式(21)至式(24)可得：

(28)

当|si|>εi时，由式(28)进一步可得：

(29)

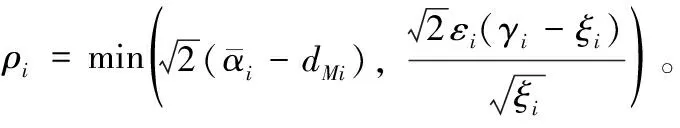
由式(29)可见，滑动变量si必能在有限时间内由初始值|si(0)|>εi收敛至|si|<εi。

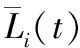
由上述分析过程容易看出，当|si|<εi时滑动变量si并不能始终维持在该零邻域内，但是能够始终保持在一个具有更大收敛半径的零邻域中。对于式(23)所示的自适应滑模控制律，当|si|<εi时显然有βi|si|≼αi(t)，此时可忽略控制律式(23)中的指数趋近项-βisi。然后再按照文献[12]的证明过程可证，当|si|<εi时滑动变量si能够始终保持在零邻域|si|<δi内。限于篇幅，关于滑动变量si的收敛域的详细分析请参阅文献[12]，本文此处不再赘述。

由以上证明过程可知，机器人系统的滑动变量si能在有限时间内收敛至零邻域|si|<δi，即机器人系统的真实滑动模态在零邻域|si|<δi内存在。

3 仿真研究

为验证本文所提出的路径跟踪控制策略的有效性，在Matlab环境中进行路径跟踪控制的数值仿真实验。BYQ-III型球形滚动机器人的物理参数分别为:

为测试本文设计的路径跟踪控制器的鲁棒性，假设实际机器人系统各物理参数与其名义值相差10%。数值仿真实验中，分别取:

设球形机器人系统的初始条件为：

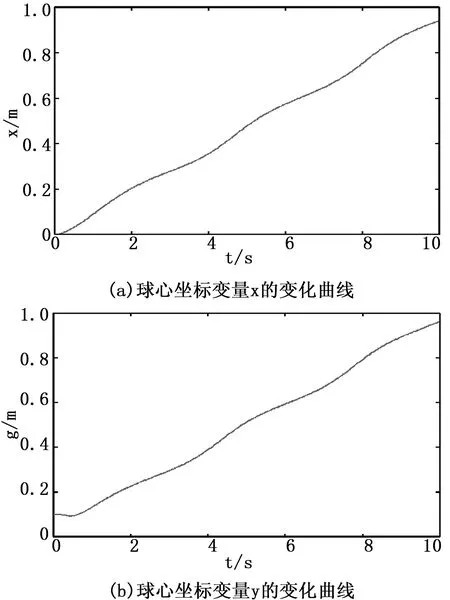
图3 球心位置的变化曲线(仿真结果)

本文设计的路径跟踪控制器的各参数分别取为：c1=4.8，c2=0.9，ε1=ε2=0.05，β1=4.5，β2=1.3，γ1=3.4，γ2=7.5，σ1=σ2=0.1，μ1=μ2=0.1。需要说明的是，所设计的路径跟踪控制器中并未计入机器人系统模型参数的变化。数值仿真实验中，选取式(30)所示的直线路径作为球形滚动机器人的参考路径：

f(x,y)=x-y=0

(30)

由式(30)可以看出，本文选取的参考路径与文献[11]选取的期望轨迹虽为同一直线，但在不同的跟踪控制问题中参考路径(或期望轨迹)的描述方式是完全不同的。

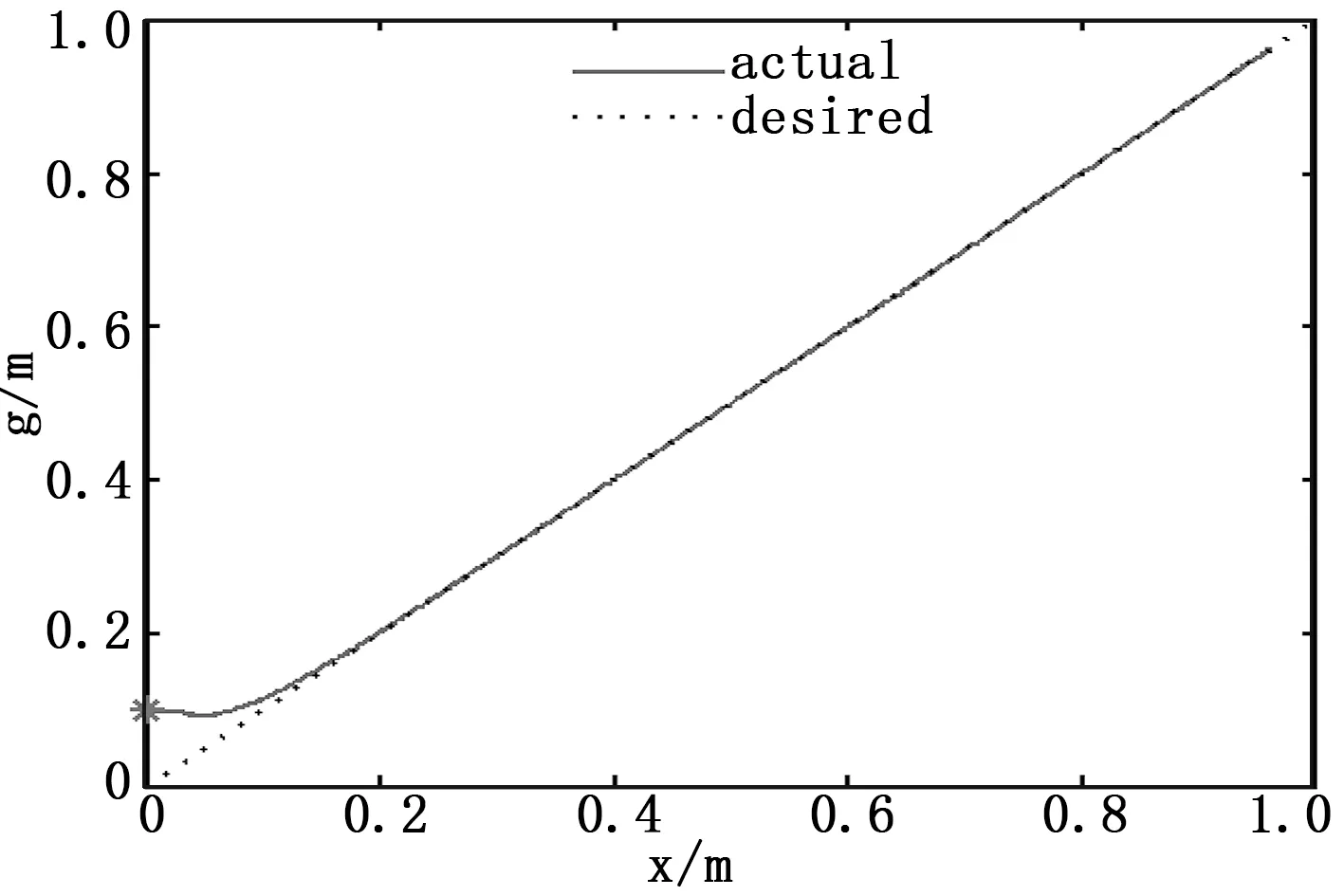
图4 直线路径跟踪的仿真结果

仿真时间设为10 s，基于自适应滑模控制算法的路径跟踪控制器的控制效果如图3和图4所示，图4中星号指示机器人的出发位置。由图3和图4可以看出，球形滚动机器人先由参考路径外的初始位置出发，经过1.7 s左右球形滚动机器人准确地到达了给定的参考路径，并在此后始终在指定的参考路径上滚动。由仿真结果可见，本文设计的路径跟踪控制器控制性能良好，被控对象中存在的参数变化不确定性得到了有效抑制，从而表明本文设计的路径跟踪控制器具有很强的鲁棒性。

4 实验结果

为进一步验证本文设计的路径跟踪控制器的有效性，利用BYQ-III型球形滚动机器人实物样机在室外的塑胶跑道上进行路径跟踪控制实验，实验环境如图5所示。路径跟踪控制实验中，借助安装在内部框架上的姿态测量系统和框架电机的光电码盘，可以得到球壳的姿态角和角速度。在此基础上，利用式(6)可得出球壳中心的速度，然后采用对速度积分的方法可以计算出球壳中心位置[11]。

图5 塑胶跑道控制实验环境

(30)

式中,ti表示第i次采样时刻，m表示采样点数量。

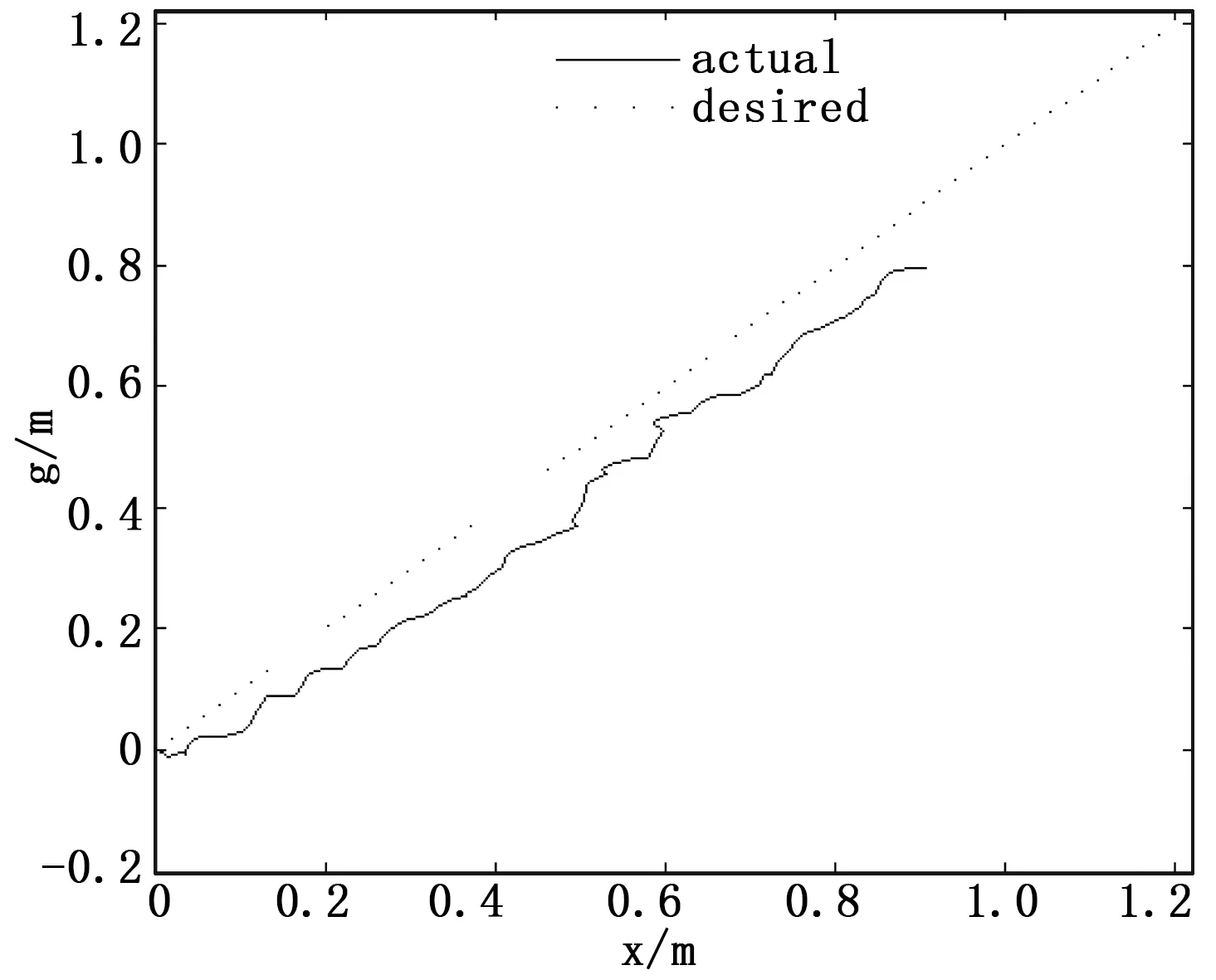
图6 直线路径跟踪的实验结果

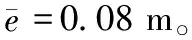
5 结论

针对一种球形滚动机器人的路径跟踪控制问题，本文提出了一种自适应滑模控制策略。所提出的控制策略无需知道有界扰动和不确定性的上界，能够通过动态调整控制器的切换增益使机器人系统在有限时间内进入真实的滑动模态。理论分析和仿真结果表明，本文提出的控制策略能够保证球形滚动机器人的实际运动路径收敛于期望的参考路径。样机实验结果进一步验证了理论分析的正确性和本文设计的滑模自适应增益控制器的跟踪性能。基于多体动力学模型和视觉定位的球形滚动机器人路径跟踪问题是本文下一步研究工作的重点。