离散Markov跳变系统事件触发H∞量化输出反馈控制

，，

(浙江理工大学 机械与自动控制学院,杭州 310018)

0 引言

Markov跳变系统作为一类特殊的随机混杂系统，不同模态之间可以通过Markov链来进行转移。由于此特性，在过去的几年中Markov跳变系统得到了学者们广泛的研究[1-2]，其中包括稳定性分析以及控制器设计等。

随着计算机和网络技术的发展，通信模式由传统的点对点方式转变为智能网络方式，网络控制系统(network control systems，NCSs)应运而生，NCSs相比较于以往的控制系统具有低成本、方便安装与维护等等优点。NCSs是通过数字通信网络将被控对象、传感器、控制器以及执行器等控制节点连接起来的闭环控制系统。但是，由于网络带宽的有限性带来了许多诸如数据包丢失、时延、量化误差等新的问题，针对这些问题在过去的几年中出现了大量的研究成果[3]。事件触发机制能够有效的避免网络化控制系统因占用大量网络资源而引起的问题因此得到了广泛的研究[4]。何为事件触发机制，即只有当采样数据满足一定条件时才能继续传输下去。相比于传统的周期触发方式，事件触发能够有效地节约网络资源。近年来，学者们提出了不同的事件触发机制来尽可能的最小化通信资源的使用。文献[5]研究了具有状态和输入双重量化的网络化奇异系统的事件触发H∞控制问题且进一步设计了状态反馈控制器。文献[6]解决了具有分组丢失的事件触发的(NCSs)的量化稳定的问题，同样的这篇文章设计的也是状态反馈控制器。然而，状态反馈控制器要求所有状态变量都是可观测的，这在实际工程中很难实现，因此输出反馈的研究随之产生。文献[7]针对Markov跳变系统，在测量输出量化的情况下研究了事件触发H∞输出反馈控制问题。Peng等[8]研究了非均匀采样网络控制系统的事件触发H∞输出反馈控制。上述两篇文章都设计了输出反馈控制器但都是针对连续系统而言的。就目前现有的研究成果来看，有关离散Markov跳变系统的事件触发机制的研究并不多。

另一种解决网络带宽有限所带来的问题的方法即为量化，在通过有限的通信信道发送信号之前量化信号是必不可少的。因此，有关控制信号量化方面的问题引起了学者们广泛的研究。Xiao等[9]讨论了单输入Markov跳变线性系统的模依赖量化状态反馈镇定问题。上述文章考虑了控制器与执行器之间的量化情况，在实际过程中传感器对被控对象采样的控制信号同样需要量化。

近几年来，关于离散Markov跳变系统的研究不断深入。文献[10]研究了具有网络诱导延迟的离散Markov跳变系统基于事件触发的H∞滤波问题。Rasool等[11]研究了具有自适应量化密度或有限信息的离散系统鲁棒H∞输出反馈控制器设计。到目前为止，将离散Markov跳变系统和事件触发机制结合的研究成果较少。

综上所述，本文研究基于事件触发机制的离散Markov跳变系统量化H∞输出反馈控制。主要工作如下：(1)为了减小网络带宽所带来的影响，引入事件发生器和量化器；(2)结合离散Markov跳变系统，建立了将事件触发方案，网络诱导时延，量化结合起来的统一系统模型；(3) 使用Jenson不等式降低系统保守性，从而获得保证系统渐近稳定且满足H∞性能指标的充分条件并设计了输出反馈控制器。

注释1：Rn和Rn×m分别表示n维的欧氏空间和n×m阶实矩阵集合，上标T和-1分别表示向量或矩阵的换位和矩阵逆。符号P>0表示P是实对称正定。I和0分别表示单位矩阵和零矩阵。diag{…}表示对角矩阵。此外，使用*表示对称矩阵的对称项。

1 问题描述

1.1 系统描述

考虑如下所示线性离散Markov跳变系统：

(1)

其中x(k)∈Rn，y(k)∈Rm，u(k)∈Rw，z(k)∈Rp分别表示状态向量，测量输出，控制输入，控制输出，ω(k)∈Rq表示服从于L2∈[0,∞)的外部扰动。A(rk),B(rk),Bw(rk),C1(rk),C2(rk),D(rk),为与rk相关的且有着适当维数的常数矩阵，系统模态rk是随着k在有限集S={1,2,3…N}中取值的Markov随机过程。πij表示从模态i跳变到模态j且满足以下条件：

Pr(rk+1=j|rk=i)=πij

(2)

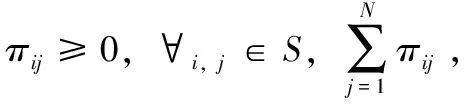
为了方便书写，当rk=i时，将A(rk),B(rk),Bw(rk),C1(rk),C2(rk),D(rk),分别记为Ai,Bi,Bwi,C1i,C2i,Di。

假设1：在系统的两个通道里都存在网络通信时延。其中，传感器与控制器之间的时延为τsc(k)，控制器与执行器之间的时延为τca(k)，总的时延为τ(k)=τsc(k)+τca(k)且τ(k)∈[τm,τM]。

假设2：传感器是时间驱动，控制器、执行器和量化器均为事件驱动。通信网络中的数据是单包传输，且没有数据包的丢失。

1.2 基于事件触发机制的系统模型

为了减少网络通信负担且保证系统性能，我们在传感器和控制器之间引入事件发生器。与文献[12]类似，当前采样数据y(k)会马上传输到事件发生器，最新的信息能否传输到控制器取决于以下条件：

[y(k)-y(sl)]TΦi[y(k)-y(sl)]>σiyT(k)Φiy(k)

(3)

其中：Φi∈Rm为待设计的正定加权对称矩阵，k∈N,sl∈N,σi∈[0,1)。y(k),y(sl)分别表示当前采样数据和最新传输数据。如果采样数据满足(3)，那么数据将会传输到控制器当中。

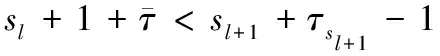
[y(sl+r)-y(sl)]TΦi[y(sl+r)-y(sl)]>

σiyT(sl+r)Φiy(sl+r)

综上我们将[sl+τsl,sl+1+τsl+1-1]分成以下几段：

(4)

定义：

(5)

接着定义误差向量：

(6)

根据(3)-(6)，当k∈[sl+τsl,sl+1+τsl+1-1]时有：

(7)

为了进一步减少通信负担，在传感器与控制器之间引入对数量化器fi(·)，假设不同模态的量化器相同因此记fi(·)=f(·)。量化器f(·)定义为f(y)=[f1(y1)f2(y2) …fn(yn)]T，对数量化器fs(ys)(s=1,2,…,n)定义如下：

(8)

(9)

设计静态输出反馈控制器为：

(10)

结合(6)～(10)可以得到:

(11)

将(11)代入(1)中，得到以下闭环控制系统：

(12)

在本节结束之前，我们给出了系统随机稳定和H∞性能指标的定义以及一些重要的引理。

定义1：当外界扰动ω(k)=0时，对任意初始条件，系统(12)满足:

(13)

那么，系统(12)是渐近稳定的。

定义2：对于任意ω(k)≠0,ω(k)∈L2[0,∞)，在零初始条件下，控制器输出z(k)满足:

E{‖z(k)‖2<‖ω(k)‖2}

(14)

则系统(12)是渐近稳定的且H∞性能指标γ>0。

引理1[16]：对于任意实数ρ，矩阵R>0,XT=X满足以下不等式：

-XR-1X≤ρ2R-2ρX

引理2[17]：对于给定的对称矩阵E1和任意适当维数的矩阵E2,E3，那么：

对于所有满足ΔT(k)Δ(k)≤I的Δ(k)，当且仅当存在ε>0时，使得以下式子成立：

引理3[18]：对于任意正定矩阵M∈Rn*n，标量d1,d2∈Z(d1≤d2)，向量w(k)∈Rn,k∈[d1,d2]，则有如下不等式成立：

2 主要结果

基于上节建立的离散Markov跳变时延系统模型，本节将给出闭环系统(12)的稳定性分析和控制器设计结论。

2.1 稳定性分析

以下将给出系统(12)渐近稳定的一个判据定理1，为接下来的控制器设计提供理论基础。

定理1 对于给定标量γ>0,τM,τm，增益矩阵Ki以及触发系数0≤σi<1，如果存在正定对称矩阵Pi>0,Q1>0,Q2>0,R1>0,R2>0,Φi>0(i∈S)，满足以下线性矩阵不等式：

(15)

(16)

其中：

Λ11=-Pi+Q1+Q2-R1

Λ33=-Q1-R1-R2,Λ44=-Q2-R2Γ1=

有限集S={1,2,3…N}。

那么，闭环系统(12)是渐近稳定的且具有H∞性能指标γ>0(此处直接写gama即可，不用强调大于0)。

证明： 针对系统(12)，构造如下所示的Lyapunov-Krasovskii 泛函：

V(k)=V1(k)+V2(k)+V3(k)+V4(k)+V5(k)

(17)

其中：

V1(k)=xT(k)Pix(k)

η(l)=x(l+1)-x(l)

当外部扰动ω(k)=0时，求ΔV(k)。

E{ΔV2(k)}=E{xT(k)Q1x(k)-xT(k-τM)Q1x(k-τM)}

E{ΔV3(k)}=E{xT(k)Q2x(k)-xT(k-τm)Q2x(k-τm)}

E{ΔV5(k)}=E{(τM-τm)2ηT(k)R1η(k)-

利用引理3的Jenson不等式可以得到：

E{ΔV(k)}≤ξT(k)∑ξ(k)

其中：

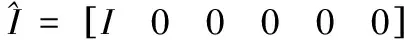
根据Schur补引理可得如果(15)～(16)成立，那么系统(12)是渐近稳定的。

接下来证明系统(12)的H∞性能，当ω(k)≠0时，可得：

E{ΔV(k)}=E{ΔV(k)}+zT(k)z(k)-γ2ωT(k)ω(k)-

zT(k)z(k)+γ2ωT(k)ω(k)=

ξT(k)Ψξ(k)-zT(k)z(k)+γ2ωT(k)ω(k)

其中：

根据Schur补引理可得(15)保证Ψ<0，因此如果(15)～(16)成立，那么系统(12)是渐近稳定的且具有H∞性能指标γ>0。证毕。

注释2：在证明定理1的过程中，通过使用Jenson不等式得到是线性系统渐近稳定的充分条件并且降低系统的保守性。在现有的文献中为了降低系统的保守性常常引入适当维数的自由矩阵，虽然此方法能够达到所需的效果可是却大大增加了计算的复杂度而Jenson不等式则可以有效的避免这个问题。

2.2 控制器设计

在定理1的基础上，我们设计了输出反馈控制器使得系统(12)渐近稳定。以下给出了具体控制器的设计方法。

(18)

(19)

(20)

其中：

βi=diag{-M1,…,-Mi-1,-Mi+1,…,-MN}

那么，闭环系统(12)是渐近稳定的且具有H∞性能指标γ>0。

证明： 矩阵不等式(15)等价于：

(21)

其中：

注释3：由于Δf为不确定项因此无法使用Matlab当中的LMI工具箱进行求解，所以需对其进行转换具体方法如下：

利用引理2可得，存在实数ε>0使得式(21)转变为以下不等式：

(22)

(23)

(24)

其中：

由于YiC1i=C1iMi不是严格的不等式，于是我们将其转化：

接着，将(16)左右同时乘以Mi可得：

(25)

利用Schur补引理可知(25)等价于(19)。

综上所述，如果(18)～(20)成立，那么系统(12)是渐近稳定的且具有H∞性能指标γ>0。证毕。

注释4：在推导定理2的过程中，最大的困难在于如何解决KiC1iMi这样的非线性项的问题。在Zha等[7]的启发下，我们成功地克服了这个问题并且针对离散Markov跳变系统提出了一种新的静态输出反馈控制器设计方法。

注释5：近些年来，尽管有一些文献已经提出了静态输出反馈控制[19]，但很难用于即存在事件触发机制又带有量化的离散Markov跳变系统。定理2给出的新方法无疑对具有量化的网络化Markov跳变系统的事件触发输出反馈H∞控制器的设计是有效的。

3 数值仿真

假设系统(12)有两个模态描述如下：

模态1：

模态2：

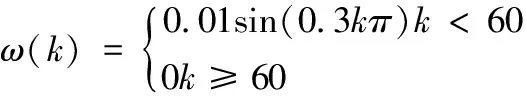
针对该系统，我们考虑以下情况。对数量化器量化指标相同δ=0.1,给定最小时延τm=0.01时。根据定理2通过求解LMIs得到不同触发系数σi与最大时延τM的关系如表1所示，从中我们可以容易地看出，触发系数越σi大，最大时延τM越小，这表示系统时延减小，但系统的性能下降。

表1 不同触发系统下对应的最大时延

当触发系数给定为σ1=σ2=0.1时，可以得到不同量化指标δ与最大时延τM的关系如表2所示，从中可以看出量化使得最大时延τM有所减小，这也表明了本文提出的能够减小网络通信负载。

综上所述，给定触发系数σ1=σ2=0.1，最大时延τM=0.5，量化指标δ=0.1，γ=4通过定理3利用LMI工具箱得到以下数据：

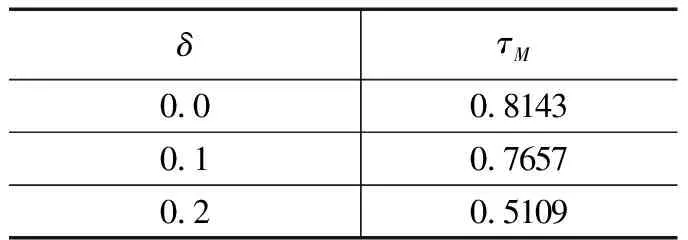
表2 不同量化指标下对应的最大时延

输出反馈增益：K1=0.0539,K2=-0.2830.

触发矩阵：

注释6：Markov 跳变系统可以用来模拟许多具有突变特性的动态系统，比如生化系统，电力系统，经济学系统以及网络控制系统等。近年来，将事件触发机制与量化结合考虑的文章有很多，例如文献[7]主要研究的是连续的Markov跳变系统，就目前而言离散Markov跳变系统方面的研究还是有限的。这就更加说明了本文研究的必要性。在本文的仿真例子中，网络时延和数据丢包存在于传感器、控制器以及执行器三者之间的信息传输通道中，而我们将这些随机特性用 Markov 链来表示，再结合事件触发和量化进而建立一个新的系统模型并对该模型进行仿真实验。

图1 模态切换图

图2 状态响应图

图3 事件触发时刻图

4 结束语

本文研究了基于事件触发机制的离散Markov跳变系统的量化H∞输出反馈控制。在考虑到网络带宽有限导致网络资源不合理利用地情况下，引入了事件触发机制来决定采样信号能否传递。另一方面在传感器与控制器之间引入对数量化器。在结合分析网络诱导时延的基础上，将事件触发，量化以及离散Markov跳变系统统一起来建立了一个新的系统模型。利用现有的数学方法得到使闭环系统渐近稳定且满足H∞性能指标的充分条件，并在此基础上进一步设计了输出反馈控制器。最后通过仿真实例说明本文设计方法的有效性。