基于IGSA优化的LSSVM制冷系统故障诊断研究

， ，，

(杭州电子科技大学 自动化学院， 杭州 310018)

0 引言

空调制冷设备已经逐渐成为人们追求舒适环境的必需品。然而制冷系统结构复杂，工作环境特殊，加上缺少定期维护与检修，使得制冷设备常常“带障”运行。制冷系统一旦发生故障，将会导致系统运行效率低下，能源成本增加，用户舒适感下降，部件磨损加剧等问题[1]。因此，对制冷系统的故障进行早期的检测与诊断显得尤为重要。

近些年来，研究人员针对制冷系统结构复杂、非线性程度高等特点，提出了许多基于数据驱动的方法来对其进行故障诊断[2]。常见的有主元分析、神经网络等[3-4]。其中神经网络方法应用较为广泛，但传统神经网络存在训练模型需要的数据量大，收敛速度慢，精度不高等缺点。

支持向量机(Support vector machine, SVM)是一种基于结构风险最小化原则的机器学习方法[5]，能够很好地平衡模型的分类精度和泛化能力，在样本量有限、系统的非线性及高维模式识别中优势显著，已经成功应用于机械、化工等领域的故障诊断中。最小二乘支持向量机(Least square support vector machine, LSSVM)是SVM的一种演变方法，它从约束条件出发，采用误差的二范数作为损失函数，并将SVM的不等式约束替换为等式约束，简化了计算，缩短了计算时间[6]。LSSVM的核参数与正则化参数的选取对模型的性能影响很大，使用较多的网格法与梯度下降法[7]寻优时间长，收敛精度不高，难以获得最优的分类模型。目前，利用粒子群(PSO)、遗传(GA)、引力搜索(GSA)等启发式算法对LSSVM的参数进行寻优是研究的热点。胡天琪等[8]用改进的粒子群算法优化LSSVM，在模拟电路的故障诊断中验证了方法的有效性。周竹等[9]用遗传算法对LSSVM的参数寻优，提高了霉变板栗的识别率。Yuan等[10]建立基于LSSVM的短期风力预测模型，并用引力搜索算法对模型参数进行寻优，提高了预测精度。

研究表明，相较于GA和PSO算法，GSA在收敛性能上有一定的优势[11]。然而基本GSA仍然存在早熟收敛，易陷入局部最优等问题[12]，依然需要对其加以改进，提高搜索性能。本文在标准GSA的基础上，引入PSO的局部搜索能力和粒子的速度更新机制，改进算法的速度公式，并将改进的引力搜索算法用于LSSVM的参数优化中，建立一种IGSA-LSSVM的制冷系统故障诊断模型。将建立好的模型用于风冷热泵机组故障模拟实验中，结果验证了算法的有效性和优越性。

1 基本原理

1.1 最小二乘支持向量机(LSSVM)

设训练集{(xi,yi)},i=1,2,…,N,xi∈Rd，其中xi是第i个输入变量，yi是相应的类别，d为样本个数。原空间的函数优化问题为：

s.t:yi[wTφ(xi)+b]=1-ei,i=1,…,N

(1)

式中，γ为惩罚因子，用来平衡模型的复杂性和训练误差，选取合适的γ可以使模型具有良好的泛化能力；ei为误差量；b为截距；w为法向量；φ(i)为映射函数，将输入空间的内积xi·xj转换为特征空间的内积φ(xi)·φ(xj)[13]。

引入Lagrange函数：

(2)

式中，αi为Lagrange乘子，分别对w,b,ei,αi求偏导，计算得到关于α和b的线性方程组：

(3)

式中，E=[1,1,…,1]T；α=[α1,α2,…,αn]T；y=[y1,y2,…,yn]T；ΩN×N为核矩阵。Ωij可由下式计算：

Ωij=<φ(xi)·φ(xj)>=φ(xi)Tφ(xj)

=K(xi,xj)，i,j=1,…,N

(4)

(5)

由上述可知，选取RBF核的LSSVM分类模型有两个参数需要确定，即约束条件中的系数γ以及核宽σ，它们的选取对LSSVM的性能有很大影响。

1.2 引力搜索算法(GSA)

GSA是一种新颖的启发式算法，由Rashedi等人于2009年根据万有引力现象而提出[11]。在GSA中，每个粒子对应着一种解决方案，所求问题的解则由粒子的位置表示。粒子之间通过万有引力作用而移动，其中质量越大的粒子拥有的吸引力更大，而且移动速度也要更慢。最终所有粒子聚集在质量最大的粒子周围，其位置对应着最优解。

(6)

其中：Maj(t)表示j的主动引力质量，Mpi(t)表示i的被动引力质量，G(t)是引力系数，ε是一个小的常量，Rij(t)是粒子i和粒子j之间的欧几里得距离。

适应度函数一旦确定，相应的引力和惯性质量就可以通过计算得出。用下列方程更新引力和惯性质量：

Mai=Mpi=Mii=Mi,i= 1,2, …,N

(7)

fiti(t)为粒子i在t时刻的适应度值，求解最小适应值时，worst(t)和best(t)的定义如下：

(8)

为了让算法具有随机特征，设d维上施加于i的合力为由其他粒子施加的引力分量的随机加权和：

(9)

randj是[0,1]之间均匀分布的随机数。

(10)

Mii(t)是第i个粒子的惯性速度。

在t+1时刻，粒子i的位置和速度可以表示如下：

(11)

(12)

1.3 改进的引力搜索算法(IGSA)

尽管GSA具有良好的优化性能，但是从式(11)和(12)可以看出，GSA的位置和速度更新只考虑了粒子当前的状态，即没有记忆性[15]。而当算法迭代运行到后期时，靠近近视最优解的粒子质量都基本相同，此时粒子的运动将十分缓慢，算法发生了停滞现象。本文提出的IGSA是在标准GSA的基础上，引入PSO的局部搜索能力和粒子的速度更新机制，使得算法在维持搜索群体多样性的同时，还能改善搜索效果。

改进后的粒子运动方程为：

(13)

(14)

为了验证改进算法的有效性，选取3个经典的基准函数来进行测试[16]。

(15)

(16)

(17)

为了公平起见，GSA和IGSA的参数均设为：搜索空间的粒子数N=30，c1=0.5，c2=1.5，w为区间[0,1]内的随机数，最大迭代次数均为1 000次。GSA和IGSA分别单独运行30次，获得3个测试函数的最优值和平均值，并计算出标准差，详细结果见表1，f1(x)、f2(x)和f3(x)的迭代曲线图如图1所示。

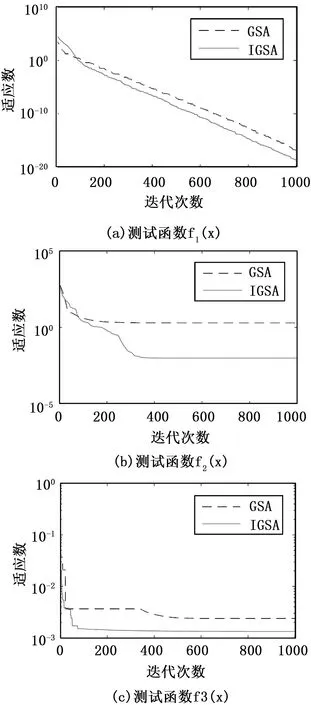
图1 GSA与IGSA优化迭代曲线对比

从图1可以看出IGSA在优化三个测试函数的表现上均优于GSA，有更快的收敛速度和更高的收敛精度。这是因为IGSA引入了历史全局最佳适应值gbest，惯性质量大的粒子受到gbest的引导，朝着全局最优解的方向移动，较好地解决了GSA后期算法停滞的问题。这为IGSA用于LSSVM的参数进行优化提供了依据。

表1 GSA和IGSA优化结果对比

1.4 基于IGSA的LSSVM参数优化

LSSVM模型构建的过程中将分类的错误率(误分率)作为适应度函数，以误分率最小化为优化目标，最优值对应的参数组合γ即为LSSVM模型的最优参数，具体步骤如下。

Step1：随机生成初始种群并初始化LSSVM的参数γ，初始化粒子数γ，最大迭代次数γ，学习因子γ，γ，确定搜索空间；

Step2：输入训练样本，对数据进行预处理及归一化，将初始化得到的γ对训练集进行LSSVM学习，并将分类的错误率作为IGSA的适应度函数，计算每个粒子的适应值；

Step3：根据公式(7)，(8)计算γ，γ，和γ；

Step4：根据公式(10)计算γ；

Step5：根据公式(13)，(14)更新粒子的速度与位置即得到的LSSVM参数；

Step6：判断程序是否迭代完成，若否，回到Step3；若是，则返回最优参数，程序结束。

2 实例分析

2.1 实验数据采集

本文的研究对象为一台分体式热泵型落地空调器，型号是：KFR-72LW，机组的额定制冷量7.2 kW，制热量是8 kW，蒸发器与冷凝器都采用了R22-空气翅片换热器，节流装置采用热力膨胀阀。在该机组的基础上，依托焓差实验台，搭建故障模拟实验系统。分析除机组正常运行(类别编号F0)的情况外，引入压缩机吸排气串气，四通阀泄漏等4种典型单一故障，如表2所示。

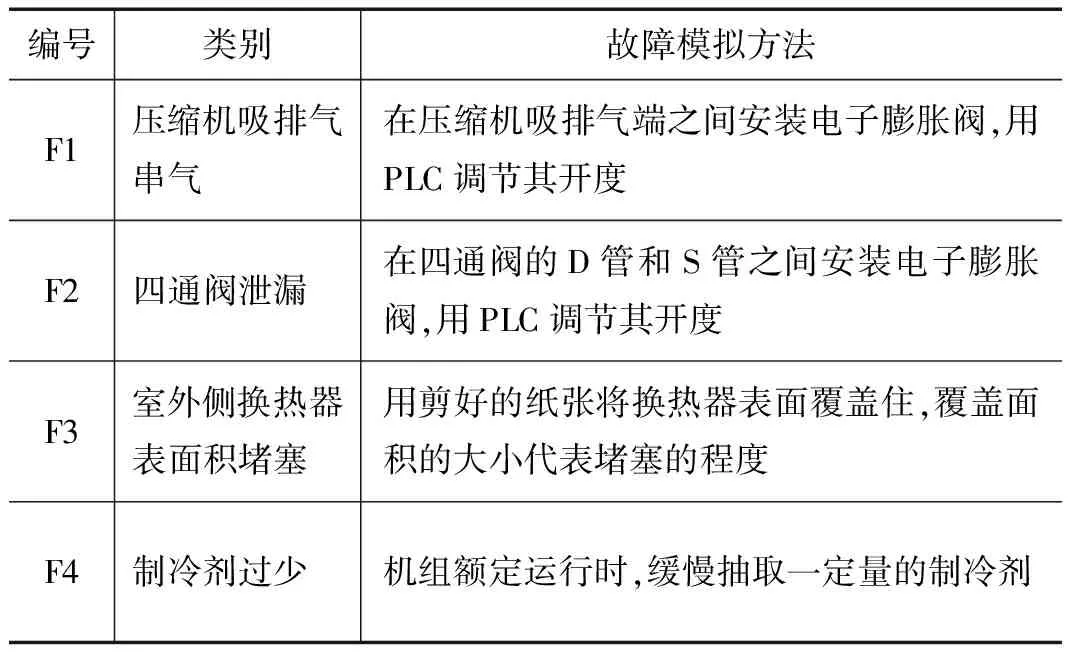
表2 故障类别及模拟方法

在搭建好的故障模拟实验台上，对需要采集的参数进行传感器布点。在实验设计中，一共设置了22个采集点位置，分别代表了机组运行的温度、压力等参数。通过数据采集系统，获取机组在制冷工况下运行的原始数据，原始样本数据由22个特征参数组成，代表了不同状态下的特征参数的变化，由γ～γ表示。部分原始样本数据见表3。

2.2 IGSA-LSSVM诊断模型

基于IGSA和LSSVM的制冷系统故障诊断模型的构建主要分为两大部分，即LSSVM模型的训练，以及将训练好的模型用于故障模式的分类。LSSVM的两个结构参数γ和σ的选取对诊断模型的性能非常重要，常用的网格法和交叉验证法收敛速度太慢，并且可能达不到全局最优。因此，本文采用IGSA算法对参数进行优化。由于标准的LSSVM只能解决二类分类问题，而本文需要将制冷系统正常运行及4中典型故障进行区分，属于多分类问题。因此，需要将多个LSSVM进行组合，常用的组合方法有“一对一”，“一对多”， “有向无环图”等[17]，本文采用实际应用广泛的“一对一”分类方法。由于有5种类别：正常、压缩机吸排气串气、四通阀泄漏、室外侧换热器表面积堵塞以及制冷剂过少，需要构建5×(5-1)/2=10个二分类LSSVM分类器，最后采用投票的方法来确定故障的类别。

IGSA优化LSSVM的故障诊断过程如图2所示，首先，对样本数据进行预处理，并将其分为训练集和测试集；然后，对IGSA算法的参数进行初始化，选择核函数构建LSSVM模型；接着，按照前文1.4节所诉，利用IGSA对LSSVM的参数进行优化获取最优参数；最后，将最优参数和训练集对LSSVM模型进行训练，构建最终的故障分类模型，并用测试集对该模型进行验证，分析故障分类结果。

图2 基于IGSA与LSSVM的故障诊断过程

2.3 诊断结果及分析

在本研究中，利用搭建好的故障模拟实验台采集机组正常运行和模拟故障的数据。原始数据可能存在噪声和异常数据，首先要将其剔除，由于故障特征参数的量纲和数量级可能不同，还需要对数据进行归一化处理。然后在正常运行及4种故障的样本数据中随机选取400组，其中300组作为训练集，用于模型的训练；100组作为测试集，用于模型的验证。IGSA的参数设置为：最大迭代次数itmax=200，粒子数N=30，c1=0.5，c2=1.5，γ和σ的取值范围分别为[0,1000]和[0,100]。经过IGSA迭代寻优后，得到最优的参数组合：γ=297.42，σ=18.25。利用优化好的IGSA-LSSVM模型对正常运行及4种故障进行区分，故障分类结果如图3所示。

表3 部分原始样本数据

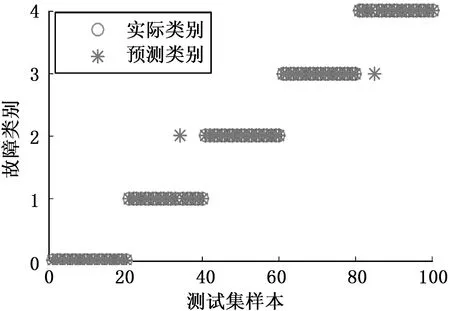
图3 故障分类结果

从图3可以看出，IGSA-LSSVM模型能够准确地将制冷系统正常运行及4种故障进行区分，准确率达到了98%。为了对比验证本文所提方法的有效性，将其与标准LSSVM，PSO-LSSVM以及GSA-LSSVM模型进行比较，其中各模型的训练数据及测试数据均与IGSA-LSSVM模型一致，PSO和GSA的参数设置均与IGSA优化算法相同。具体的诊断性能如表4所示。

表4 故障诊断结果对比

从表4可以看出，IGSA-LSSVM诊断模型性能最好，准确率达到了98%。表明改进的引力搜索算法对于LSSVM的参数寻优能力更强，所得的诊断结果也更为准确。而标准的LSSVM模型由于人为选取参数的盲目性，诊断性能最差，准确率只有83%。同时GSA-LSSVM的准确率为92%，高于PSO-LSSVM的90%，说明GSA的寻优能力要强于PSO。由于标准的引力搜索算法缺少记忆性，容易陷入局部最优，本文提出的IGSA算法借鉴粒子群算法中的记忆性思想，改进速度更新机制，能有效地减少振荡，跳出局部最优，获得更优的参数组合，取得更好的故障诊断结果。

3 结束语

LSSVM用于制冷系统故障诊断时，对故障模式的分类性能很大程度取决于核函数参数和惩罚因子的选取。由于人工设置参数可能导致故障识别不准确，本文提出了一种改进的GSA算法来优化参数，建立了IGSA-LSSVM的制冷系统故障诊断模型。仿真结果表明，改进的GSA能够快速收敛到全局最优。故障模拟实验表明，IGSA-LSSVM模型能够对风冷热泵机组的正常运行及4种故障进行准确区分，提高了故障诊断的准确率。同时，与标准的LSSVM，PSO-LSSVM以及GSA-LSSVM模型进行对比，表明了所提方法的优越性，在制冷系统故障诊断方面具有良好的应用前景。