基于递推法的CRC-32校验码并行改进算法

左飞飞，杜英森，刘剑霏

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

在数据的传输过程中由于空间电磁环境复杂等原因，可能会产生误码，即某几位数据0变为1，或1变为0，导致接收端得到错误的数据。为了降低误码率，通常对数据进行特定编码，在收发端进行额外的验证，使接收端能发现某些错误，进而实现纠错功能，常用的编码方法有CRC-32校验码、CRC-16校验码、汉明码、奇偶校验法等[1]。其中32位循环冗余校验(Cyclic Redundancy Check)简称CRC-32校验在性能和资源消耗两方面都有较大的优势，因而，在无线电通信、SATA硬盘数据传输等系统中，CRC-32校验是最常用的检错手段之一[2]。

计算CRC-32校验码有两类方法：一类方法是将CRC-32校验码生成过程转换为对应的逻辑门电路，将这样的门电路固化在系统的整体电路中，它的优点是计算速度快，但由于它是专门为固定的通信系统设计的电路，所以无法更改和移植，并且专门设计和集成的成本较高[3]；另一类是编程实现，在众多编程实现的途径中，FPGA和CPLD由于其可并行计算、可反复修改的特性使其在CRC-32的计算中有较大优势。

编程实现CRC-32校验码生成程序有两种传统方法：一种为串行算法，一种为查表法。这两种是循环调用的函数，设置一个CRC寄存器，设置寄存器初始值后，依次根据输入数据进行计算，更新CRC寄存器的数值，直至对数据处理完毕，CRC寄存器最终存放的数据即为CRC值[4]。这两种方法都能实现运算目的，但串行算法由于需要一位一位地计算运行结果，导致运行速度过慢，查表法由于需要存储所有的运算结果，导致占用空间过大。

引信应用环境最大的特点就是过载数值大、体积小，在这样的前提下进行筛选，现在使用的某品牌QFN封装CPLD的最小体积可小至5 mm×5 mm，但是由于这样的FPGA或CPLD一般是入门级产品，寄存器位数通常只有100～300左右，在这样的条件限制下，需要提出一种新的CRC-32校验码生成方法，能够根据不同芯片寄存器空间的限制，最大限度的利用存储空间提升运算速度。

在CRC-32校验码生成方法中，固定电路成本高且缺乏灵活性，传统按位串行算法计算速度慢、查表法需要额外占用空间，本文针对此问题，提出了基于递推法的CRC-32校验码并行改进算法。

1 传统CRC-32校验码的生成算法

CRC校验的基本原理如下[5]：CRC校验发收端的首要工作是确认系统所采用的生成多项式G(x)，任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应，例如：代码1010111对应的多项式为x6+x4+x2+x+1，而多项式x4+x3+1对应的代码为11001。校验码的具体生成过程为：假设要发送的信息用多项式C(x)表示，将C(x)左移R位(可表示成C(x)×2R)，这样C(x)的右边就会空出R位，这就是校验码的位置。用C(x)×2R除以生成多项式G(x)得到的余数r(x)就是校验码，将它们组合起来，变为{C(x),r(x)}并发送出去，这样发送的数据就是一个能被生成多项式G(x)整除(模2除)的码多项式。接收端收到{C(x),r(x)}后，用它除以生成多项式G(x)，如果余数为0，则说明传输过程中无错误发生，否则说明传输有误。

由上述可知，生成多项式G(x)是构成CRC校验码的关键。并不是任何一个多项式都可以作为生成多项式，从检错与纠错的要求出发，生成多项式应能满足下列要求：1)任何一位发生错误都应使余数不为0；2)不同位发生错误应当使余数不同；3)应满足余数循环规律。国际上常用的几种CRC校验码及其生成多项式如下所示[6]：

CRC-12：x12+x11+x3+x2+x+1，

CRC-16:x16+x15+x2+1，

CRC-CCITT:x16+x12+x5+1，

CRC-32:x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1。

生成多项式的G(x)位数越高，检错能力就越强，由于CRC-32的可靠性，把CRC-32用于重要数据传输，在通信、计算机等领域运用十分广泛。

1.1 串行算法[7]

依据CRC校验码的产生原理来设计程序，寄存器每输入8位或16位待计算数据后更新一次，以8位为例说明该算法。

图1 每次输入1字节的CRC-32串行算法Fig.1 Byte-wise serial algorithm for CRC-32 check code

这种方法的思路与CRC校验码的生成原理一致，优点是可读性强，占用空间小，模块代码较少，修改灵活，可移植性较强，缺点也很明显，每位数据都要进行一次移位与异或计算，计算量大，速度慢。

1.2 查表法[8]

查表法的基本原理是把所有会出现的CRC码全部计算出来，放在一个表里，每次进数据通过查表得到当次结果，省去了计算时间，可大大提高运行速度。对于CRC-32来说，共有256组32位的数据需要提前存储在处理器的寄存器中，寄存器中的一部分数据如下：

查表法的优缺点基本与串行计算法相反，由于每次计算只需查表即可得到答案，因此它的运行速度很快，但是相对的，存储这样的一个查找表至少需要占用256×32=8 192位寄存器，占用空间对于寄存器较少的CPLD或入门级FPGA过大，另外这样的查找表一旦约定的寄存器初始值不同或选择的特征多项式不同，整个表内的所有值都需要重新计算，几乎没有可修改性，移植性较弱。

2 基于递推法的CRC-32校验码并行改进算法

串行算法虽然速度慢，但其每次计算过程在逻辑上都完全按照CRC-32校验码的生成原理，每次串行算法的结果与初始值之间的逻辑关系可以由CRC-32校验码生成原理经过简单的推导转化成并行逻辑关系。根据这样的思路，可以将第一次串行算法的结果作为第二次串行算法的初始值，再将第二次串行算法的结果作为第三次串行算法的初始值，按照这样的规律层层递推n次，就可以直接得到并行输入任意n位数据时CRC寄存器中新老数据之间的并行逻辑关系。

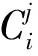
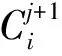
(1)

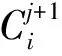
(2)

(3)

(4)

基于递推法的CRC-32校验码并行改进算法以递推法为基础，根据实际情况中不同的计算速度和占用空间的需求，计算出并行输入任意n位数据时CRC寄存器中新老数据之间的并行逻辑关系，并根据这一逻辑关系修改程序，从而达到在一定占用空间的限制下，最大程度提升运算速度的目的。

3 仿真验证

为了具有代表性，本文在仿真验证过程中分别并行输入16位数据、8位数据、4位数据的递推并行算法进行验证。

基于第2章所使用的CRC-32特征多项式，类似上面的推算，我们可以分别得出并行输入16位数据、8位数据、4位数据的CRC低6位更新逻辑，其中并行输入4位的CRC-32更新逻辑(低6位)如下所示：

crc_new[0]=crc_old[28]^data_in[0];

crc_new[1]=crc_old[28]^crc_old[29]^data_in[0]^data_in[1];

crc_new[2]=crc_old[28]^crc_old[29]^crc_old[30]^data_in[0]^data_in[1]^data_in[2];

crc_new[3]=crc_old[29]^crc_old[30]^crc_old[31]^data_in[1]^data_in[2]^data_in[3];

crc_new[4]=crc_old[0]^crc_old[28]^crc_old[30]^crc_old[31]^data_in[0]^data_in[2]^data_in[3];

crc_new[5]=crc_old[1]^crc_old[28]^crc_old[29]^crc_old[31]^data_in[0]^data_in[1]^data_in[3]。

3.1 正确性仿真验证

首先验证本文提出方法的正确性，编写Verilog程序，在ISE软件环境下进行编译后，设定同样的初始值、输入数据，如果得到的结果相同，则证明该算法无误，反之说明算法不正确。

设定初始值32′hFFFFFFFF，取输入数据为32′h12345678，使用并行输入16位、8位、4位数据的递推并行算法运行程序，输出结果为32′h4A090E98，再通过查表法与串行算法分别进行计算，发现三者得到的结果一致，证明本文提出的计算数据无误。

3.2 占用空间与计算速度的仿真验证

3.3.1占用空间对比

在ISE软件中，程序设计占用寄存器数量等片上资源在Design Summary中可以直观的看到，分别截取16位、8位、4位递推并行算法、串行算法和查表法的界面即可做出比较。

根据图2、图3可以看到：并行输入16位、8位、4位数据的递推并行算法占用寄存器分别为449个、225个和68个；查表法占用寄存器2 095个；串行算法占用寄存器32个。

3.3.2计算速度对比

随机输入一串长度为1 000位的数据，在ISE自带仿真器中对比得出最后结果的时刻数字，如图4、图5所示。根据图4、图5可以看到：本文提出的递推并行算法与查表法、串行算法所得结果相同并且均为正确结果，其中并行输入16位、8位、4位数据的递推并行算法分别在第106、190、315个时钟周期得出正确结果，查表法在第59个时钟周期得出正确结果，串行算法在第2 107个时钟周期得出正确结果。

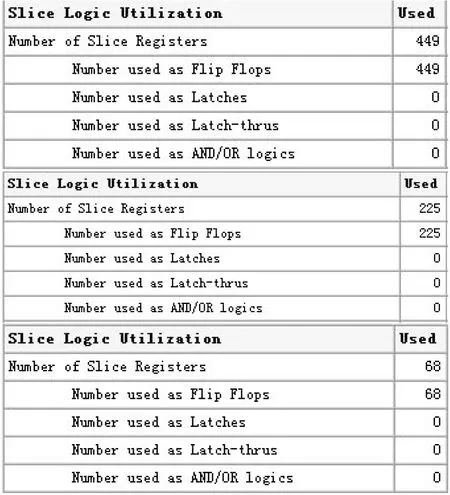
图2 16位、8位、4位并行算法占用空间统计Fig.2 Numbers of slice registers of 16/8/4 bits parallel algorithm

图3 串行算法和查表法占用空间统计Fig.3 Numbers of slice registers of serial algorithm and the look-up table method

3.3 仿真结果分析

根据3.1节、3.2节，将仿真数据汇总在表1中做比对，其中，占用空间s越小越好，处理时间t越短越好。

图4 并行输入16位、8位、4位递推并行输入算法计算时间Fig.4 Time consumptions of slice registers of 16/8/4 bits parallel algorithm

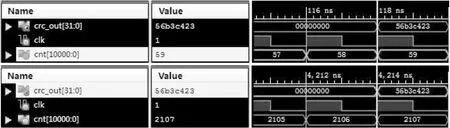
图5 查表法与串行算法计算时间Fig.5 Time consumptions of slice registers of serial algorithm and the look-up table method

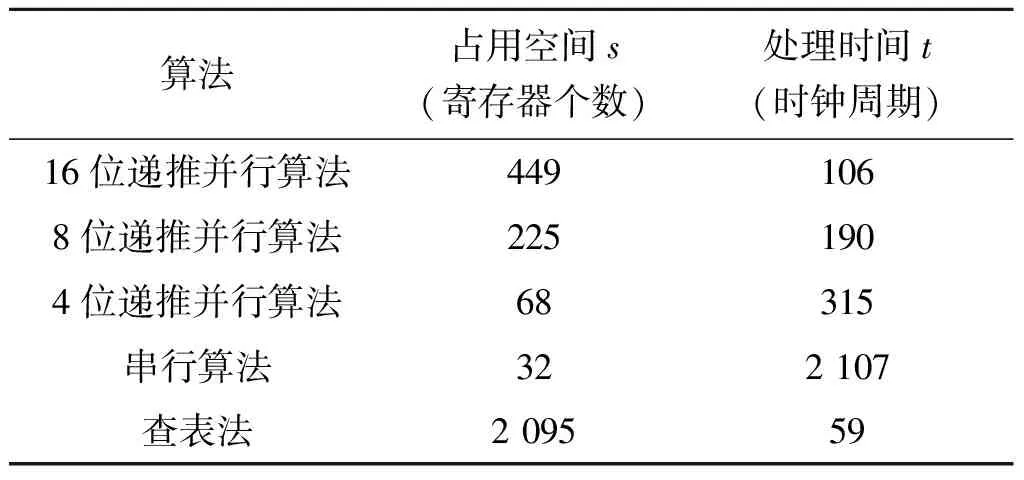
算法占用空间s(寄存器个数)处理时间t(时钟周期)16位递推并行算法4491068位递推并行算法2251904位递推并行算法68315串行算法322 107查表法2 09559

通过比较数据可以看出，本文提出的算法在不同寄存器数量的限制下，比传统方法计算速度更快。并行输入16位、8位、4位数据的递推并行算法的仿真结果说明，本文提出的基于递推法的CRC-32校验码并行改进算法速度快于按位串行计算的方法，存储空间小于查表法，有利于小型化、快速化的硬件实现。

4 结论

本文提出的基于递推法的CRC-32校验码并行改进算法以递推法为基础，根据实际情况中不同的计算速度和占用空间的需求，计算出并行输入任意n位数据时CRC寄存器中新老数据之间的并行逻辑关系，并根据这一逻辑关系修改程序，从而达到在一定占用空间的限制下，最大程度提升运算速度的目的。仿真结果表明，本文提出的基于递推法的CRC-32校验码并行改进算法速度快于按位串行计算的方法，存储空间小于查表法，有利于小型化、快速化的硬件实现。