基于谱熵的单通道多跳频信号参数盲估计方法

曾晓宇，矫文成，孙慧贤

(陆军工程大学石家庄校区，河北 石家庄 050003)

0 引言

跳频(Frequence Hopping，FH)通信是扩频通信的主要类型之一，具有保密性好、抗干扰能力强、截获概率低、组网能力强等优点，是国内外军事通信的主导手段。跳频通信的广泛应用使得无线频谱的使用情况变得更加复杂与多变，尤其是在固定地域内非合作式跳频通信的情况下，为了避免不同信号间的冲突、提高频谱的使用效率，需要通信设备在没有信号先验知识的情况下具有估计空域内跳频信号参数的能力。

跳频信号参数的盲估计问题，从接收机方面考虑可以分为单通道接收下的方法与多通道接收下的方法。单通道接收下的处理方法包括：时频分析方法[1]，稀疏线性回归方法[2]等；多通道接收下的处理方法有：谐波恢复方法[3]、盲源分离方法[4-5]、子空间投影方法[6]。单通道接收实现简单、对硬件要求低，但对多信号的处理能力有限且方法本身具有不能分辨同步跳频信号的缺陷；多通道接收由于使用阵列天线、引入了信号到达方向(Direction Of Arrive，DOA)的概念、增加了空间维度的信息，使得准确性更高性能更强，但对硬件设备的要求也更加苛刻。

军事通信中的跳频通信设备大多是便携设备，对硬件体积、规模都有严格的限制，配置以单天线居多，所以本文的研究主要针对单通道接收下的异步混合跳频信号参数估计。单通道接收下，研究接收信号为单一跳频信号的文献较多[1,7-8]，基本原理都是利用跳频信号时频脊线的周期性或者局部极值来进行参数估计，当同时存在多个信号时该方法就无法使用。而研究接收信号为混合信号时的文献较为匮乏，文献[9]提出了一种基于时频重心的方法，能够在其他定频干扰信号存在时完成跳频信号参数的估计，但是跳频信号的个数仍然只限于一个。文献[10]提出了一种基于小波包的单通道方法，能够同时实现多个跳频信号的参数估计，但是该方法需要收发双方共享先验信息，不能实现全盲估计。本文针对此情况，提出了基于谱熵的单通道多跳频信号参数盲估计方法。

1 基础理论

1.1 跳频信号

跳频信号可视为一个多分量信号，每个分量由基本信号通过时移和频移得到，每个分量表现为常数频率的指数信号[9]。单一跳频信号表达式为：

(1)

式(1)中，P代表信号功率，T代表跳频周期，rectT(t)代表宽度为T的矩形窗，fk代表跳频频率，θ代表跳变时刻，n(t)代表信号噪声。

数目为N的多个跳频信号，其混合信号的表达式为：

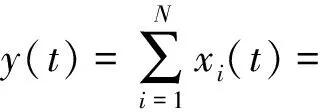
(2)

1.2 谱熵

谱熵是一种反映信号频谱的分布状态的变量，在时频变换得到时频矩阵M(t,f)的基础上，信号x(t)在第t个时刻点的谱密度定义为：

(3)

由式(3)可以看出，0≤P(t,f)≤1，同时，∑P(t,f)=1(f=1,2,…,N)。结合Shannon信息熵定义，定义信号x(t)在t时刻的谱熵为：

(4)

1.3 PRI变换

脉冲重复间隔(Pulse Repetition Interval，PRI)变换多用于混合脉冲周期信号的分选，可以盲识别出混合周期信号中各分量信号的周期值[11]。跳频时刻的集合可以模型化为单位冲激函数的和，其表达式为：

(5)

式(5)中，M为跳频时刻点的总个数；hi为跳频时刻集合中第i个元素的值，即第i个跳频的时刻。

跳周期的变换谱为：

(6)

用|G(τ)|表示跳周期的谱线。变换后，在真实的跳周期上会出现峰值，经过筛选后可得到跳周期集合。筛选根据观察时间、消除子谐波以及消除噪声的原则，设定门限为[12]

(7)

式(7)中，α，β，γ为可调参数，Ck为第k列脉冲串的脉冲个数，T为观测的总时间，ρ为跳时刻密度。

2 基于谱熵的单通道多跳频信号参数盲估计方法

在单通道接收的情况下，由于时频脊线法在盲估计跳频信号参数时无法适用于多个跳频信号同时存在的情形，本文通过使用谱熵函数来对多跳频信号进行参数的盲估计。

2.1 多跳频信号的谱熵

根据1.2节中的定义，任一时刻的谱熵可以抽象为n元变量(n由频率分辨率决定，等于时频矩阵中列向量的维数)的函数

(8)

自变量间的限定条件为：

(9)

从式(2)可以看出，多个跳频信号的混合信号在时频域上具有稀疏性，即在任一时刻的频率占用会根据信号数目集中分布在一个或多个离散的频率簇上，将这些频率簇的集合记为Λ。那么会存在xi≫xj(xi∈Λ,xj∉Λ)的现象，根据式(9)的限制，可以得到xj(xj∉Λ)近似等于零，又因为limx→0x·lgx=0，说明稀疏处频点对谱熵产生的影响可以忽略，那么式(8)将简化为：

(10)

假设跳频信号的数目为N，理想情况下集合Λ中频率簇的个数恒为N，但是实际上由于时频变换中的时间窗存在一定时间长度，当信号在某时刻发生频率跳变时，该时刻频谱会被展宽，所以跳频点时刻的集合Λ中频率簇个数m会增加并处于区间(N,2N]之中。现实中不同信号的谱密度是存在一定差异的，但为了便于定性分析，假设每一个信号都是完全平等的，即∀xi,xj∈Λ,xi=xj，综合式(9)，式(10)进一步简化为：

(11)

从式(11)中可以看出，某一时刻的谱熵与集合Λ中频率簇个数m成正相关关系，故跳频点时刻的谱熵会大于非跳频点时刻，即跳频点时刻的谱熵会出现正向突变，而谱熵正向峰值的位置又对应了谱熵函数一阶导函数的零点，所以谱熵函数可以反映多跳频信号的跳频时刻信息。

2.2 方法流程

基于谱熵的单通道多跳频信号参数盲估计方法的主要流程如图1所示。单通道接收机得到原始信号为时域波形信号，首先通过时频变换将信号从时域投影到时频域，得到信号的时频矩阵；然后基于时频矩阵计算谱熵函数，并从谱熵函数中获取所有的跳频时刻；最后通过PRI变换，从混合的跳频时刻中提取出不同分量的跳频周期。

图1 基于谱熵的单通道多跳频信号参数盲估计方法的主要流程
Fig.1 Main flow of blind estimation method for single-channel multi-hopping signal parameters based on spectral entropy

3 仿真结果及性能分析

为了验证上述方法的可行性和分析性能指标，本文对分别进行了三组仿真实验。

仿真输入信号统一为混合的两个异步跳频信号，其理论参数为：信号1的跳速为2 000 hops/s(即跳周期为500 μs)，跳频归一化频率的集合为{0.46,0.42,0.38,0.34,0.30,0.26}；信号2的跳速为1 600 hops/s(即跳周期为625 μs)，跳频归一化频率集合为{0.24,0.20,0.16,0.12,0.08,0.04}。采样频率为1 MHz，仿真时间8 192 μs，噪声为高斯白噪声。

实验一 使用STFT时频分析方法，信号为全驻留跳频信号(驻留时间等于跳频周期)。

图2(a)和(b)分别展示了信噪比为10 dB下信号的时域波形与时频域分布。图2(c)表明，在跳频时刻点处，谱熵曲线呈现正向峰值，通过谱熵的峰值提取，能正确得获取多跳频信号的跳频时刻。跳频时刻经过模型化并进行PRI变换后，通过阈值判别得到跳周期的估计值，如图2(d)中所示，在理论跳周期500 μs及625 μs附近，出现了高于阈值的峰。说明该方法能达到预期目的，实现对多跳频信号周期的盲估计。经过100次蒙特卡罗仿真，信噪比与检测成功率如表1所示(当两个估计值与理论值的差距均不超过5%时视为估计成功)。

表1 实验一的信噪比与检测成功率

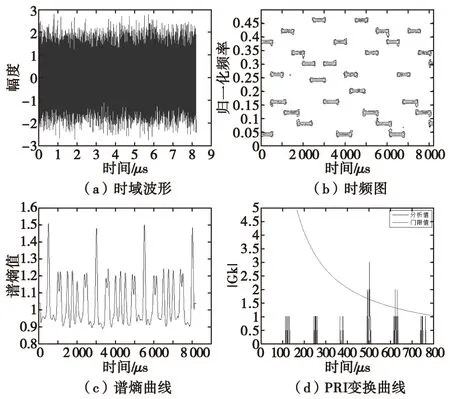
图2 实验一仿真结果(SNR=10)Fig.2 Experiment 1 simulation results(SNR=10)

实验二 使用全驻留跳频信号，时频分析方法分别使用STFT、WVD和SPWVD。

图3展示了使用不同的时频分析理论，在不同信噪比下分别重复进行100次蒙特卡罗仿真，得到周期估计的成功率与成功时周期估计均方根误差。周期估计的均方根误差计算公式为：

(12)

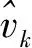
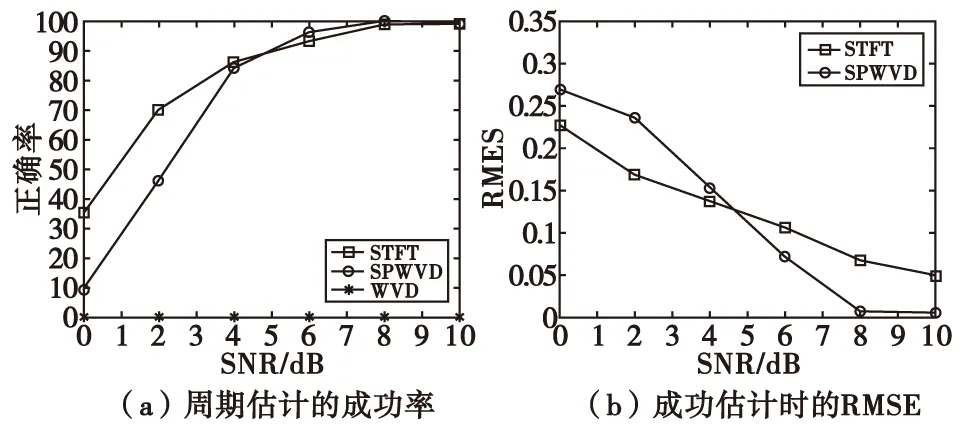
图3 实验二仿真结果Fig.3 Experiment 2 simulation results

图3(a)表明，估计结果与使用的时频分析方法密切相关：基于STFT与SPWVD时频方法的估计结果较为理想，对SNR大于6 dB时，两种时频分析下的检测成功率皆高于90%，一致性较好；当SNR小于4 dB时，两种时频分析下的检测成功率都会大幅下降，但SPWVD的下降更加剧烈。而基于WVD方法，完全无法正确估计信号参数，分析其原因是WVD中交叉项干扰严重。从图3(b)中可以看出，在正确估计跳周期的前提下，当SNR大于5 dB时，SPWVD的估计均方根误差要低于STFT的估计均方根误差，说明前者的估计精度更高；而当SNR小于5 dB时，呈现相反情况。

实验三 使用STFT时频分析方法，信号为驻留时间为90%跳频周期的跳频信号。

对比图2与图4，直观上可以看出当跳频驻留时间减少时，时域频域图像存在明显空缺部分，谱熵曲线对跳频时刻反映更加模糊，PRI变换曲线在跳频时刻的峰分辨更加困难，但依旧能正确估计跳频周期。表2展示了在实验三条件下，经过100次蒙特卡罗仿真得到的信噪比与检测成功率。对比表1与表2，当信号从全驻留跳频信号换成驻留时间为90%跳频周期的信号时，高信噪比下检测成功率的饱和值从99%下降到73%，整体检测成功率下降了约25%。说明跳频滞留时间的减少会恶化本方法的检测估计结果。

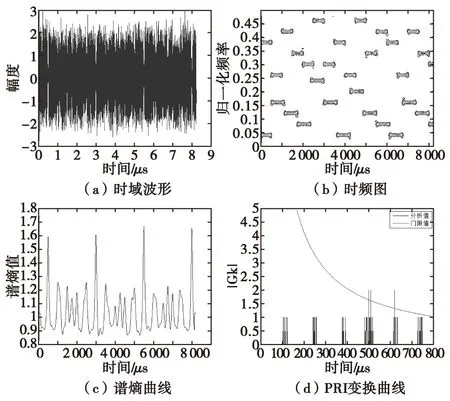
图4 实验三的仿真结果(SNR=10)Fig.4 Experiment 3 simulation results(SNR=10)

综合上述结果，本文提出的算法在时频分析不存在交叉项干扰时，能够实现对多跳频信号跳周期的盲估计。就STFT与SPWVD时频分析而言，当信噪大于6 dB时，两者的检测成功率相近且接近饱和，但SPWVD检测精度更高；而当信噪比低于4 dB时，STFT的检测成功率要高于SPWVD。但是，跳频驻留时间的减少会降低算法的检测性能。

4 结论

本文提出了一种单通道接收下基于谱熵的多跳频信号跳周期盲估计方法。该方法在时频分析的基础上，利用谱熵函数完成了对异步跳频信号中跳频时刻的全盲估计，并进一步利用雷达信号处理中的PRI变换，估计了不同分量信号的跳频周期。仿真结果表明，该方法以不存在交叉项干扰的时频分析方法为基础时，能达到预期目的。信噪比大于6 dB时，使用STFT与SPWVD时频方法皆能保证90%以上的检测成功率与0.1以下的均方根误差值，而SPWVD时频方法的检测精度更高。但是本文提出方法的检测性能会因为跳频信号的跳频驻留时间的减少而降低。本文方法为单通道接收多跳频信号的参数盲估计提供了新的思路，跳频驻留时间对本文方法影响的定量关系以及如何将本文方法与其他各种改进的时频分析方法相结合以提高检测性能有待进一步研究。