基于局部熵的超声信号阈值降噪方法

张 洪，张 郁，王通德

(1.江南大学机械工程学院江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122；2.国网电力科学研究院江苏南瑞恒驰电气装备有限公司，江苏 无锡 214161)

0 引言

超声检测作为五大常规无损检测技术之一，是目前国内外应用最广泛、使用频率最高且发展较快的一种无损检测技术，已经被国家相关法规列为特种设备检验的必要环节[1]。然而在金属材料的超声检测中，例如奥氏体不锈钢等粗晶材料的晶界会对超声波起散射作用，造成结构噪声，从而使缺陷信号被噪声污染甚至湮没[2]。因此，采用合适的信号处理方法，抑制金属晶粒引起的结构噪声，有利于缺陷回波信号的识别，从而提高检测结果的正确率。

目前，超声信号的降噪方法一般依据噪声信号与缺陷信号的频域概率分布差异，通过傅里叶变换、小波变换、经验模态分解(Empirical Mode Decomposition, EMD)等方法对信号进行分解，然后再对分解的结果进行降噪处理。傅里叶变换无法同时在时域和频域上获得较好的局部化性质，目前已经很少使用。小波变换则需要选择小波基函数和分解层数，是非自适应性的[3]，降噪效果受参数选择的影响较大。而EMD及其改进方法不需要先验获得信号和噪声的统计特性，即可自适应地分解信号，适用范围更广。

使用EMD及其改进方法将信号分解为多个本征模态函数(IMF)分量之后，还需要对这些IMF分量做进一步的降噪处理。目前常用的IMF分量降噪方法沿用了小波领域的阈值降噪法[4-5]，此方法对高斯白噪声的降噪效果较好，但对结构噪声的降噪效果则不佳。基于此，本文针对传统IMF分量降噪方法的不足，提出了基于局部熵的金属材料超声信号阈值降噪方法。

1 基本原理

1.1 CEEMDAN算法

EMD可以自适应地将非线性、非平稳的信号分解为一系列频带不同的IMF分量和残余分量之和，并且将IMF分量按照瞬时频率的差异从高到低排列起来。虽然EMD克服了小波变换的最优参数选择问题，但是其存在模态混叠现象，限制了信号分解的效果。

集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)是一种噪声辅助数据分析方法，通过在原信号中多次添加白噪声，分别进行EMD分解，然后对多次EMD分解得到的IMF分量取平均值，求得最终的IMF分量。这种方法虽然能够有效地解决模态混叠问题，但分解过程中添加的白噪声无法完全消除，且平均次数的多少严重影响了信号的重构误差。即使增加计算次数可以减小重构误差，但也会严重影响分解的计算效率。

具有自适应白噪声的完整集成经验模态分解 (CEEMDAN)方法在EEMD的基础上进一步改进，在EMD分解的每个阶段添加自适应的白噪声，可在较少的平均次数下使重构误差几乎为0。因此CEEMDAN不但可以解决EMD分解的模态混叠问题，同时也可以解决EEMD分解的重构误差与平均次数相矛盾的问题。

CEEMDAN分解算法的具体步骤如下：

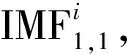
(1)

残余分量r1(t)=x(t)-IMF1。

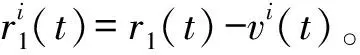
(2)

残余分量r2(t)=r1(t)-IMF2。

3)重复上述的分解步骤n次，且每一次分解后都会得到IMFi分量和残余分量，直到满足EMD分解的终止条件。最终得到的分解结果为

(3)

1.2 熵理论

信息论中，信息熵用事件发生的概率的倒数来表示该事件的信息[6]。设pi(i=1,2,3,…,n)为系统某一状态发生的概率，则该状态所具有的信息量可用如下公式定义：

(4)

式(4)中，概率pi具有如下性质

(5)

使用所有状态含有的信息量的数学期望值作为系统的信息熵

(6)

2 超声信号的局部熵阈值降噪算法

使用CEEMDAN分解信号得到如式(3)所示的IMF分量，再对IMF分量进行阈值降噪。传统方法依据信号的长度与方差等参数来确定降噪阈值，但此方法未对CEEMDAN分解进行优化，用于IMF分量降噪时效果不佳。本文针对IMF分量的降噪方法进行优化，使用信号的熵作为阈值的选取依据。

然而，直接使用式(6)计算出的信息熵，反应的是整体信号的信息量，无法用来衡量某一个信号点的含噪状态，也就难以作为阈值的选取依据。因此改进信息熵的计算方法，提出能够反映信号局部性质的局部熵，并以此作为信号阈值降噪的依据。

2.1 一维信号的局部熵

一维信号局部熵的计算方法类比了图像处理领域的二维信号局部熵[7]，建立尺寸为w的窗口，则一维信号x(t)在时间坐标轴上t0处的邻域为(t0-w/2,t0+w/2)。根据式(6)，计算这个邻域内信号的熵值Sw(t0)，作为信号点x(t0)在窗长度w下的局部熵。对每个信号点做如上处理，即可获得所有信号点的局部熵Sw(t)。

不同信号的局部熵数值范围可能不同，为了提高局部熵在阈值降噪中的通用性，对局部熵做线性归一化处理,使其分布范围为0到1之间：

(7)

局部熵反映了信号的离散程度，在均匀区域中局部熵比较大，在异质区域中局部熵比较小[7]。常见的缺陷可等效为圆柱状缺陷[8]，对超声波的反射次数较少，因此缺陷回波属于均匀信号，局部熵较大；而金属晶粒对超声波起多次散射作用，因此晶粒造成的结构噪声属于异质信号，局部熵较小。这个缺陷回波信号与结构噪声信号之间的局部熵差异，即为本文阈值降噪算法的理论依据。

2.2 超声信号的局部熵校正

如图1所示，超声波声场中存在主声束和副瓣声束[9]。而超声波的能量主要集中在半扩散角θ0以内，即主声束的范围为2θ0。2θ0以外为副瓣声束，其含有的能量在波源附近衰减很快[1]。因此本文仅考虑主声束被材料晶粒散射而造成的结构噪声。

设超声波传播时间为t，超声波在金属材料中的传播速度为c，金属材料单位面积内的晶粒数目为Zs。在时刻t，主声束的波阵面为一个球冠面，则球冠最大开口部分圆的半径r=ctsinθ0，球冠的高h=ct(1-cosθ0)，由此计算出的球冠的面积为Scq=2πrh=2πc2t2sinθ0(1-cosθ0)，此时超声波的主波束所能检测到的晶粒数目为：

Q=ZsScq=2πZsc2t2sinθ0(1-cosθ0)

(7)

式(7)中只有t为变量，其它参数为常量。可见超声波传播的时间t越久，所检测到的晶粒数量就越多。

图1 波源声束示意图Fig.1 Diagram of ultrasonic beam source

根据文献[8]中的式(13)可知，晶粒的数目越多，由晶粒造成的散射回波也就越多，即结构噪声越杂乱。因此超声波的传播时间较短时，所能检测到的晶粒数目较少，结构噪声的杂乱度较低，局部熵也就较大；反之超声传播时间越长，结构噪声的局部熵也就越小。

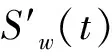
(8)

为了使校正后局部熵的数值仍然分布在0到1之间，需要对其再做一次如式(7)的线性归一化处理。

(9)

式(9)中，E(·)为数学期望。

2.3 局部熵阈值降噪算法

使用CEEMDAN分解信号x(t)，得到分量IMFi(i=1,2,…,n)和残余分量r(t)。使用相关系数法[10]确定需要降噪的IMF分量：计算IMFi与原信号x(t)之间的相关系数，并取相关系数为中等程度相关及以上的分量IMFj(j∈i)作为需要降噪的分量。

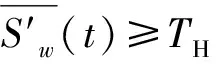
(10)

式(10)中α为降噪系数，其函数的形式如图2所示。

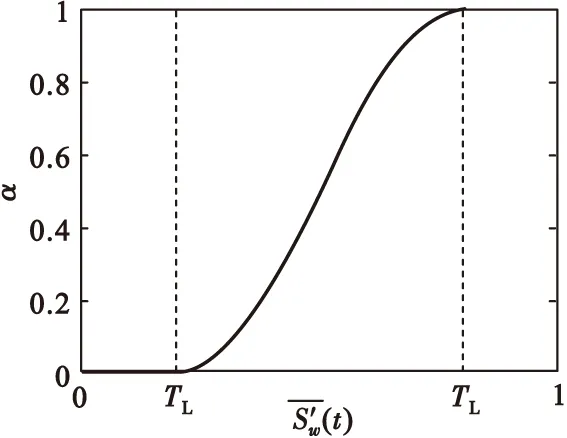
图2 降噪系数α函数图Fig.2 Function diagram of De-noising coefficient α

则降噪后的IMF分量为

(11)

经降噪后得到的超声信号x′(t)为

(12)

2.4 超声信号的消噪方法

基于局部熵的超声信号阈值降噪方法的具体实施步骤如下：

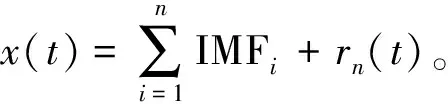
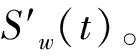
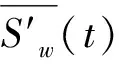
4)计算IMFi与原信号x(t)之间的相关系数，选取中等程度相关及以上的分量IMFj(j∈i)作为需要降噪的分量。

3 试验与分析

3.1 数据来源

目前通用的仿真方法，无法控制超声信号在不同时刻的局部熵数值，因此也就无法证明2.2节理论的正确性。因此，本文使用实测的超声信号为研究对象，分别对比了局部熵校正前与校正后的降噪效果、局部熵最优计算窗口长度与一般窗口长度下的降噪效果、传统方法与本文方法的降噪效果，以证明本文提出方法的有效性。

实测信号如图3所示，检测仪器为友联PXUT-910超声探伤仪，检测对象为压力容器钢X型对接焊缝，焊缝厚度为108 mm，焊缝宽度为50 mm，检测标准为JB/T4730.10-2010。

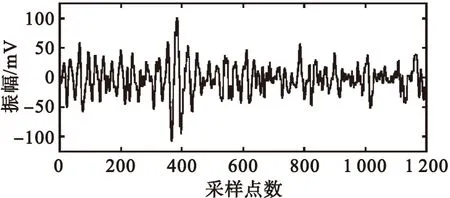
图3 实测超声信号Fig.3 Measured ultrasonic signal

3.2 降噪效果对比

常用的降噪效果评价指标为信号的信噪比和均方差，但根据其定义[11]，这两个指标的计算过程必须以纯净信号为基准。纯净信号为仅含有用波形，且不含有噪声波形的信号，仿真试验中可以很容易地获取这个信号，但实测信号实验中却很困难。因此本文以信号降噪前后的波形对比图作为标准，来评判降噪方法的有效性。

将实测超声信号x(t)进行CEEMDAN分解，分解后得到的IMF分量见图4。从图4中可以看出，超声信号x(t)被分解为9个IMF分量，但其中哪些分量的噪声属于结构噪声仍然未知，需要使用相关系数法来确定。计算IMFi(i=1,2,…,9)与原信号之间的相关系数，结果如表1所示(保留3位小数)。

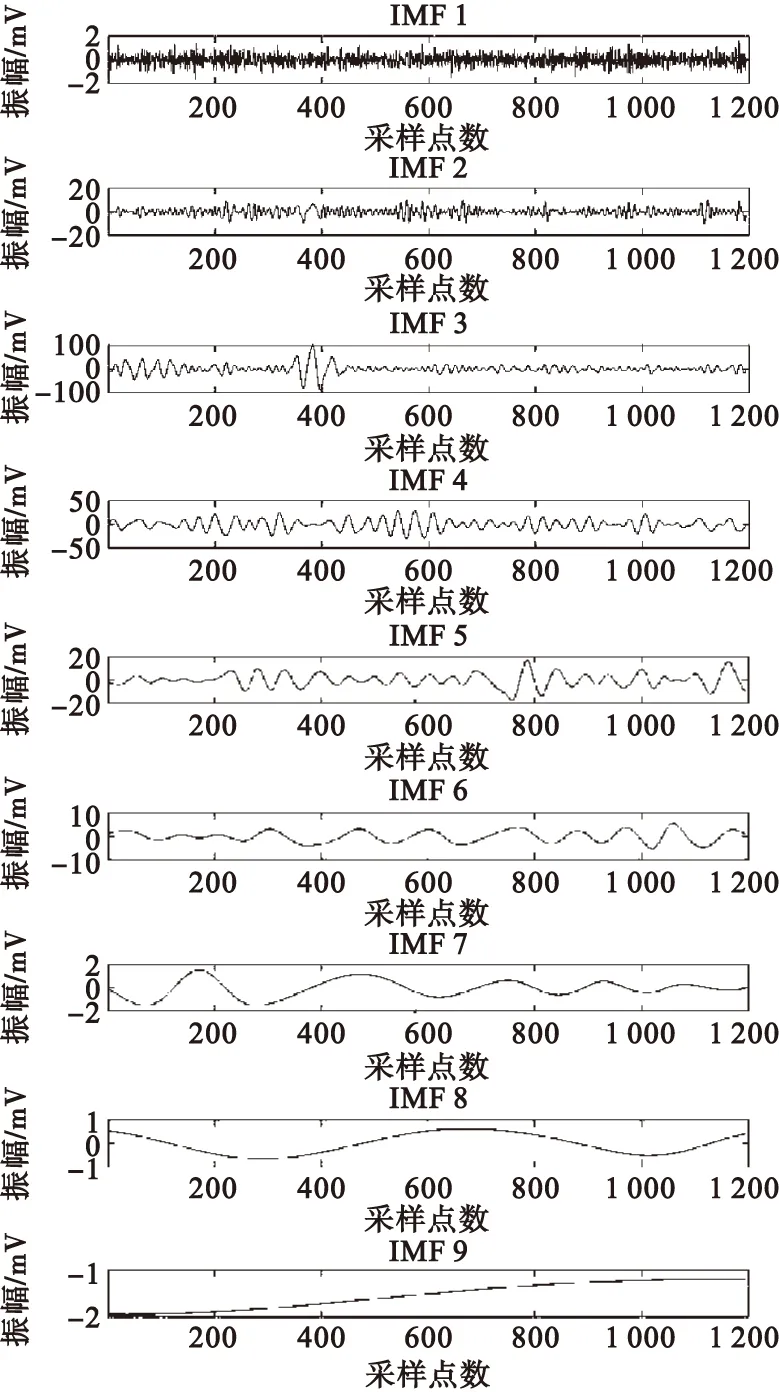
图4 CEEMDAN分解结果Fig.4 Decomposition results of CEEMDAN

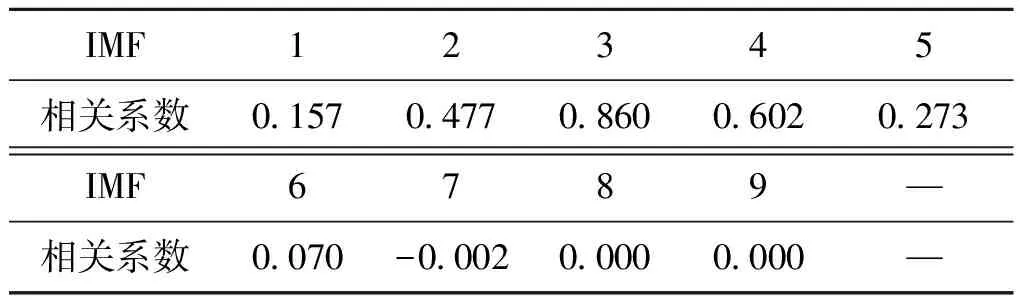
IMF12345相关系数0.1570.4770.8600.6020.273IMF6789—相关系数0.070-0.0020.0000.000—

根据Pearson相关系数定义的中等程度相关，取相关系数为0.4及以上的IMF分量为需要降噪的分量。由表1中的相关系数值可知，结构噪声所在的分量为IMFj(j=2,3,4)，这些分量需要按照本文提出的方法进行处理；IMF1为高斯白噪声分量，不属于本文研究内容，使用传统方法[12]进行处理;IMFk(k=5,6,…,9)为趋势分量，不作处理。

3.2.1局部熵的校正及其降噪效果

初步选取局部熵计算窗口长度w为100，计算图3所示超声信号x(t)的局部熵，并依据式(7)作线性归一化处理,结果如图5所示。

图5 局部熵及其校正Fig.5 Local entropy and its correction

从图5中校正前的局部熵可以看出，局部熵的大体趋势随着时间的增长而减小，这符合2.2节中关于超声波传播特性对局部熵数值影响的分析。

为了消除局部熵随着时间增长而减小的趋势，对校正前的局部熵进行一元线性回归分析，得到一元线性方程，然后从校正前的局部熵数值中减去这个趋势方程，即可得到校正后的局部熵。一元线性方程及校正后的局部熵如图5所示。

分别以校正前与校正后的局部熵为降噪参数，取阈值TH=0.8，TL=0.2,使用式(10)、式(11)对IMFj(j=2,3,4)进行降噪，再使用式(12)重构IMF分量得到降噪后的信号，降噪效果如图6所示。

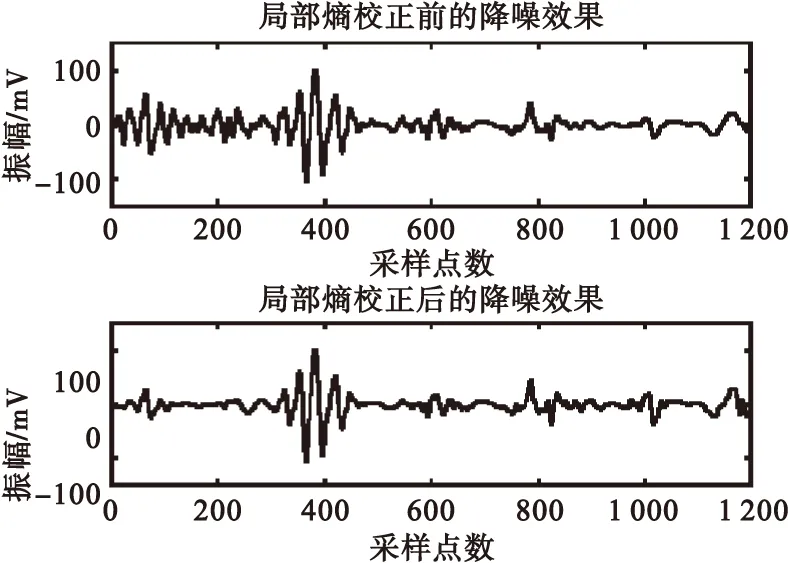
图6 局部熵校正前后的降噪效果Fig.6 De-noising effect by local entropy before and after correction

从图6中可以看出，使用校正前的局部熵作为降噪参数时，虽然信号后半部分的降噪效果较好，但前300个采样点的信号降噪效果较差。而使用了本文提出的方法校正局部熵之后，再进行降噪时，不论是信号的前半部分还是后半部分，都得到了较好的降噪效果。

3.2.2窗口长度的选取及其降噪效果

窗口长度w决定了每个时刻的局部熵是由多少个信号点计算而来的。为了研究不同的窗口长度对降噪效果的影响，分别取w为50，100，166，200，250，300时，计算超声信号x(t)的局部熵，然后进行降噪处理，其中w=166是依据式(9)计算出的最优窗口长度。降噪后的信号波形如图7所示。

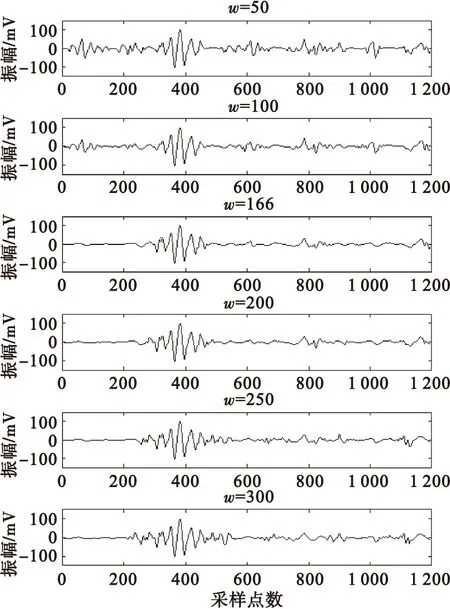
图7 不同窗口长度下局部熵的降噪效果Fig.7 De-noising effect of local entropy under different window length

当窗口长度过小时，窗口内的信号只能存在较少的幅值状态，也就是相均质。这导致了部分噪声信号的局部熵值偏大，在进行降噪处理时被当作了有用信号，从而被保留下来。从图7所示降噪对比图中可以看出，当w=50时，信号中仍保留有较多的噪声；而当w从50扩大到166时，降噪的效果越来越好。

当窗口长度过大时，有效信号附近的噪声信号则更容易被保留下来。计算这些噪声信号的局部熵时，由于窗口长度过大，部分有效信号也会被包含进来，这部分有效信号会拉高噪声信号的局部熵，从而使噪声被保留下来。如图7所示，当w从166扩大到300时，有效信号两端的噪声信号越来越多。

依据本文提出的方法选取最优窗口长度(w=166)，再进行信号的降噪处理，从结果中可以看出，不论是整体的降噪效果，还是有效信号附近的降噪效果，都得到了提升。

3.2.3与传统方法的对比

使用小波变换及CEEMDAN结合传统的阈值算法对信号进行降噪，与本文提出的方法作对比。其中小波变换选取db4小波函数将信号x(t)分解到第5层，采用Rigrsure方法确定阈值，选取硬阈值函数和软阈值函数中降噪效果较好的一组结果作为对照；CEEMDAN方法的阈值和阈值函数选取方式同上。三种方法的降噪效果如图8所示。

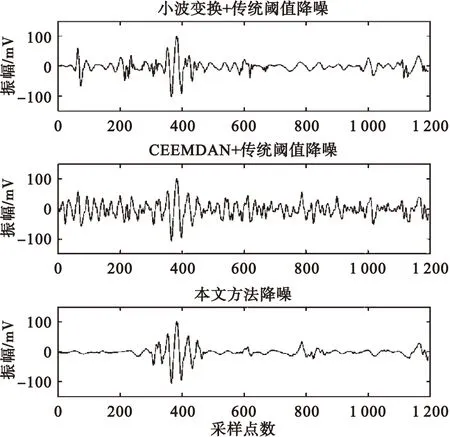
图8 不同方法的降噪效果Fig.8 De-noising effect of different methods

从图8中可以看出，小波变换结合传统阈值算法的降噪方法，对结构噪声占主导的超声信号有一定的降噪作用，但是降噪后的信号仍保留有较多的噪声。CEEMDAN结合传统阈值算法的降噪方法，由于没有针对IMF分量的特性进行优化，因此降噪效果极为有限。而本文提出的方法，不仅在整体的降噪效果上优于小波变换，而且对有效信号的保留也更加完整，更有利于信号的分析与识别。

4 结论

本文提出了基于局部熵的超声信号阈值降噪方法。该阈值降噪方法首先计算出一维超声信号的局部熵，并根据超声波在金属材料中的传播原理，对局部熵的数值进行校正，同时还确定了局部熵的最优计算窗口长度选择方法。最后结合局部熵，提出了适用于IMF分量的阈值降噪公式，用以取代现有的IMF分量阈值降噪方法。试验结果表明，在对实测超声信号的降噪过程中，经过该阈值降噪方法处理过的信号，能够有效地消除绝大部分的结构噪声，且尽可能地保留了有用信号，降噪效果优于小波变换及CEEMDAN结合传统阈值算法的降噪方法。