基于数据驱动的迭代学习算法在导弹 突防能力评估中的应用

邹 慧

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

保证可靠的发射和稳定的飞行，是实现导弹有效攻击的前提条件。迅速地突破各种阻击和干扰，最后实现战斗部爆炸损伤目标，是武器作战能力的重要体现。导弹突防能力又称导弹空中生存能力，指导弹能够穿透敌方拦截系统而不被损伤的能力。根据导弹的特点和作战应用的实际情况，对其突防能力评估进行了建模研究，对导弹作战效能评估有重要的意义。

基于数据驱动的迭代学习算法[1]表示仅使用输入和输出数据得到系统最优跟踪性能，可以避免费

时的辨识试验，通过多次反复执行就能改善系统性能。指数标度法完全适用韦伯-费希纳心理学定律，应用指数标度法进行导弹突防能力评估的主要任务是合理构建主观感觉判断矩阵N，并计算客观差异判断矩阵M的排序权值。

本文在构建导弹突防能力评估的递阶结构模型上，利用(0，2)标度法[2]构造客观差别判断矩阵，采用数据驱动迭代学习算法同时优化矩阵中相邻2层的客观重要度，并检验矩阵的一致性和计算矩阵的排序权重。结果表明，基于数据驱动的迭代学习算法在用于导弹突防能力的评估中简单通用，具有较高的应用价值。

1 突防能力指标评估体系的递阶层次模型

1.1 基于迭代学习算法的指数标度法

基于迭代学习算法的指数标度法包括下面5个步骤[3]：

步骤1：建立分层递进模型,它包括零优选目标层X、准则层Y和方案层Z。准则层Y包括要考虑的准则、子准则，这些准则和子准则可由若干层组成。

步骤2：利用上个层次的要素为准则对Y层(涵盖子准则层)的各要素两两比较，利用(0,2)标度构建Y层的主观感觉判断矩阵N={cij|i，j=1～n}，在矩阵N中cij=2,如果i元素比j元素重要，写1；如果i元素与j元素重要度相同，写0。

步骤3：将主观感觉判断矩阵N转化为客观差别判断矩阵M。计算矩阵N中各个元素的重要性排序指数：

(1)

计算矩阵B={bij|i,j=1,…,n}n×n，其中:

bij=ari-rj

(2)

式中：a(a>1)为相邻两级的比率。

步骤4：使用迭代学习算法优化矩阵M中的a，并且计算排序权值ωi，i=1，…，n。又因为矩阵M的定义为：

(3)

如果矩阵M满足公式(3)，那么矩阵M具有完全一致性，于是有：

(4)

(5)

从上面可以看出，公式(5)左侧的值越小，矩阵M的一致性就会越高。若公式(5)等号成立，那么矩阵M就具有完全的一致性。鉴于此，将Y层中每个因素的单次排序和一致性检查的问题归结为以下问题：

(6)

(7)

在公式(7)中，一致性指标函数CIF(n)，wk(k=1,…,n)作为排序权值向量，比率参数a是优化变量。公式(6)是一个线性优化问题并且很难用传统方法求解，然而解决该问题的一个简单但有效的方法是迭代算法。如果CIF(n)<0.1，则矩阵M具有令人满意的一致性，并且用这种方法计算的每个元素的排序wk和参数a是可接受的。

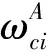
(8)

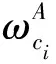
1.2 迭代学习算法

迭代学习控制具有严格的数学描述和详细的理论分析，它是智能控制领域的一个重要分支。迭代学习理论自诞生以来，经过国内外学者的研究，其理论体系不断完善。该算法的基本原理如图1所示。

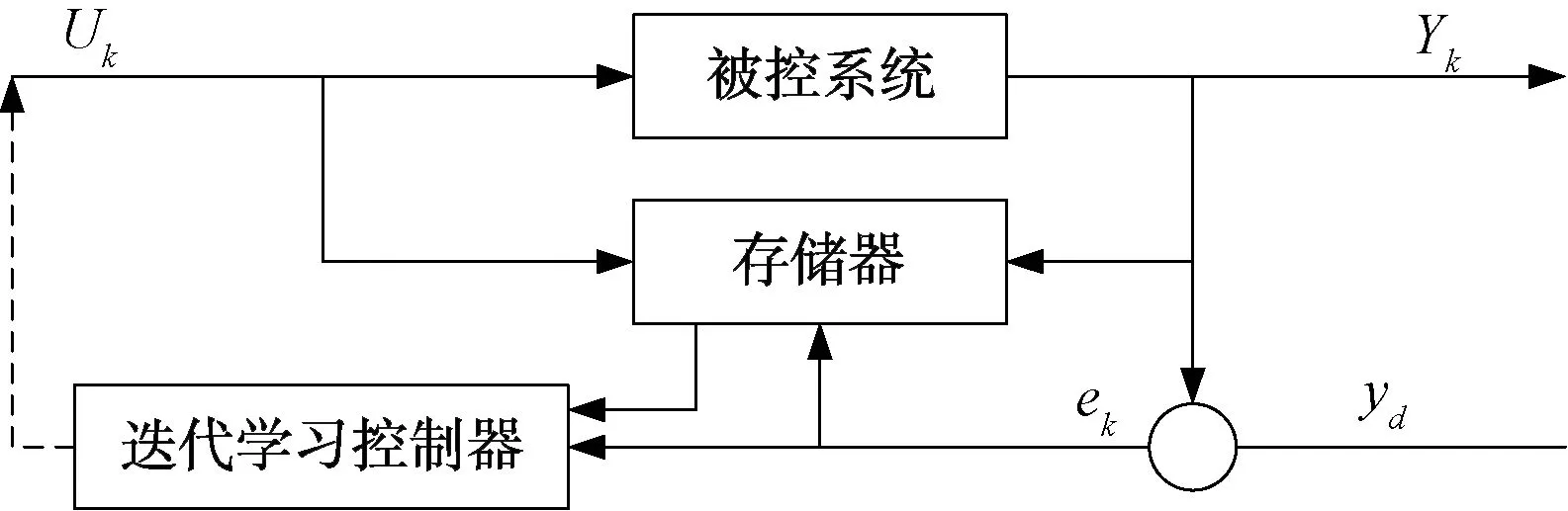
图1 迭代学习控制技术理论基本原理图

由图1可知，系统的第k次控制项uk作用于被控系统，并输出yk。因此，假定要跟踪的系统信号期望轨迹为yd，可以得到第k次输出误差公式为：

ek=yd-yk

(9)

将uk、yk、ek存储到存储器中，可知系统第k+1次控制项uk+1是由第k次控制项(uk)以及误差项(ek)经过映射后得到。从以上可以看出，迭代学习控制基本规律的经典数学描述为：

uk+1=F(uk，ek)

(10)

式中：F()表示映射关系。

考虑图1的迭代学习控制基本原理，工作流程可详细表示为：

(1) 设置u0为系统的初始状态控制项序列，yd为跟踪信号期望轨迹。

(2) 当第k批次控制项序列uk作用于被控系统时，对应于系统输出项的序列为yk。

(3) 此时系统跟踪误差项序列ek将根据控制算法自动计算，控制项uk、输出项yk和误差项ek等将由系统自动存储，根据迭代学习控制律可以计算出uk+1。

由此可知，应用迭代学习控制技术的目的是在可控的时间[0,T]中，搜索出控制项uk,使得该控制项作用于被控系统时，系统输出项yk可以迅速追上期望轨迹yd，并且最终顺利实现任务。

虽然传统的迭代学习控制有较好的性能，然而它在学习律的增益参数选择方面仍然有严重的对设计者的依赖。另一方面学习律的增益在系统控制中起着不可替代的作用，所以国内外的很多研究学者将优化理论引进这一领域中，设计并优化满足特定要求的性能指标，最终得到最优学习律。以下就是最为经典的迭代学习控制技术优化理论——迭代学习控制牛顿优化算法。

迭代学习控制牛顿优化算法具有较快的收敛速度，它通常用于求解复杂的非线性方程组。求解该算法的基本思想是对非线性方程进行线性化，并通过线性方程求解，可以得到近似零点[4]，基本方程为：

(11)

国外学者Konstantin设计了Newton 法求解连续非线性系统的迭代学习控制器[5]，yk=F(uk)为该方法的系统模型。其中uk∈U，yk∈Y，且U

和Y均为Banach空间，映射关系F()在 Banach 空间满足F:U→Y。

通过上述模型，迭代学习控制的学习规律设计如下：

uk+1=uk-[F′(uk)]-1(yd-yk)

(12)

1.3 递阶层次模型

突防能力是导弹的重要性能指标，也是影响导弹系统作战效能的最重要因素之一。 在导弹武器系统的演示中，评估导弹突防能力具有十分重要的意义。为提高导弹突防能力，需进一步针对一体化的突防干扰体系(如图2所示)进行分析。

图2 导弹突防干扰体系组成

根据上述干扰系统中分析的影响地地导弹突防能力的主要因素，建立了导弹突防能力的评价指标体系，构建了较为简化的地对地导弹突防能力评价指标体系的层次模型，如图3所示。

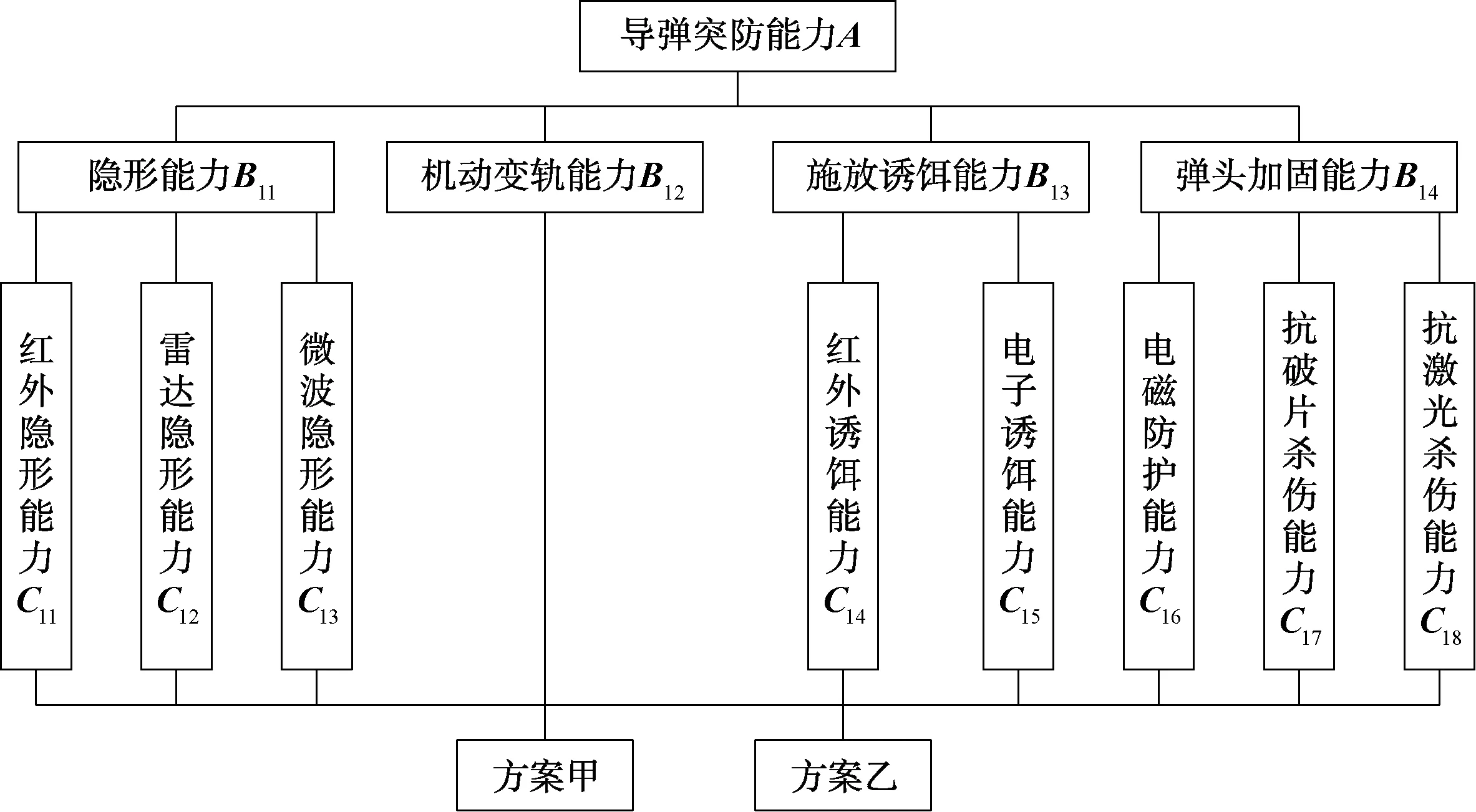
图3 导弹突防能力的递阶层次结构

2 应用分析

本节应用基于迭代学习算法的指数标度法对甲、乙2种型号的地地导弹突防能力进行评估。

采用基于数据驱动的训练方法对输入的样本进行训练，构造出B层上的各要素，如表1所示。

表1 训练样本

数据网络训练结果如下：

采用基于迭代学习算法的指数标度法，可以得到以X层为判据的主观感觉判断矩阵M。各评价指标的权重分别为W1=0.157、W2=0.478 9、W3=0.274 2、W4=0.089 9、参数a=1.321 5，相应的一致性指标函数值是0.000 069。得出子准则层主观感觉判断矩阵M11、M13、M14的评价指标的权值见表2。

表2 主观感觉判断矩阵B11、B13、B14的 各评价指标的权值计算结果

假设机动变轨能力B12、红外隐身能力C11、雷达隐身能力C12、微波隐身能力C13、红外诱饵能力C14、电子诱饵能力C15、电磁防护能力C16、抗破片损伤能力C17和抗激光损伤能力C18分别为WB12、WC11、WC12、WC13、WC14、WC15、WC16、WC17、WC18，利用上述GA-ESM得到的结果，计算每个合成的权重，如表3所示。

表3 合成权重计算结果

甲、 乙2种地地导弹各项指标值如表4所示。

表4 甲、乙2种地地导弹的各项指标值

根据上述指标，导弹甲和导弹乙的突防能力可以分别计算为X1=0.489，X2=0.510，又因为X1

3 结束语

针对现有导弹突防能力评估系统的局限性，建立了地对地导弹突防能力评估的分层模型，采用基于迭代学习算法的指标标度法优化矩阵中相邻2层的客观重要度，检验矩阵的一致性，计算矩阵的排序权重，对导弹突防能力进行了评估。结果表明用本文方法进行评估，将定性分析与定量分析相结合，是有效和可行的。