土中中风化嵌岩抗拔桩承载机理研究

，，，，，

(1.贵州大学 土木工程学院，贵阳 550025; 2 东南大学 交通学院，南京 210096； 3.贵州师范大学 材料与建筑工程学院， 贵阳 550025)

1 研究背景

抗拔桩广泛应用于大型地下室抗浮、高耸建(构)筑物抗拔、海上码头平台抗拔、悬索桥和斜拉桥的锚桩基础、大型船坞底板的桩基础和静荷载试桩中的锚桩基础等。在地下水位较高的地区，当上部结构荷重不能平衡地下水浮力的时候，结构的整体或局部就会受到向上浮力的作用，如：地下水池、建筑物的地下室结构、污水处理厂的生化池等必须设置抗拔桩。嵌岩抗拔桩作为钻孔灌注桩的一种重要类型，单桩承载力高、沉降量小的特点较为显著[1]，适合应用于较大范围的中风化、较破碎的岩层(如：贵州地区)，在工程中得到广泛的应用，尽管如此，但嵌岩抗拔桩工程中的理论研究滞后于工程应用研究，尤其贵州中风化岩层中抗拔桩承载特性的研究很缺乏。但是，国内外学者对抗拔桩承载力特性也做了相关方面的研究。

国内学者，何思明[2]在前人研究基础上，假设桩端破坏面在桩端处并与其相切，破坏面与水平面的夹角为45°-φ/2(φ为土的内摩擦角)，构造出桩土破坏面方程dz/dx=tan(45°-φ/2)N(N为破裂面参数)，根据极限平衡原理，建立平衡方程，利用极值定理求出土体抗拔桩极限承载力；唐孟雄等[3]利用幂函数形式的滑移面假定，采用极限平衡法，推导出一种计算基岩内抗拔桩极限承载力的方法；王光满等[4]结合工程实例，对在复杂岩溶地质条件下嵌岩抗拔桩的设计进行了研究；王耀辉等[1]对模型嵌岩桩试验进行了数值对比分析。

国外学者提出很多计算抗拔桩极限承载力的模型，如：假设破坏面为圆柱面的标准模型[5]、Meyerhof理论模型[6]、Das理论模型[7]、倒圆锥台模型[8]、Chattopadhyay理论模型[9]、Shanker理论模型[10]以及Kotter方程求解模型[11]等。然而，这些模型只适合计算土质地基中的抗拔桩极限承载力，并不适用于桩、土(岩)组合地基的嵌岩抗拔桩极限承载力计算。

从已有的现状来看，目前对嵌岩抗拔桩承载特性的理论和试验方面研究较少，抗拔桩极限承载力计算理论主要聚焦于土质地基中，理论研究滞后于工程应用，且抗拔方面的原位试验较少，尤其土中中风化嵌岩抗拔桩承载机理研究尚未有报道。鉴于此，结合实际工程现场试验数据，对中风化地区数值模型进行合理的选取，建立合理的模型并运用FLAC3D对嵌岩抗拔桩进行数值模拟，对其承载特性进行分析，研究成果可为相关类似工程提供一定指导。

2 抗拔桩原位试验

2.1 工程概况

某工程地基为岩溶地基，基础等级为二级，场区为负地形，场区地下水静水位高程为1 257.0 m；场区地势低洼，地表水易于汇集，汇水面积大，根据场地水文地质情况调查及贵州雨季经常出现极端天气分析，该工程需考虑地下水位对建筑物的影响以及工程重要性等级，并该工程区的地基进行抗浮设计。由工程的岩土工程勘察报告，工程区地层及岩性分布情况见表1。拟建工程采用旋挖灌注桩作为抗浮桩，工程试验桩的设计参数见表2，拟采用基础形式塔楼为独立基础+筏板基础或桩基础，其单桩设计竖向抗拔极限承载力为1 200，2 700 kN。

表1 场地土层概况Table 1 Soil profile on site

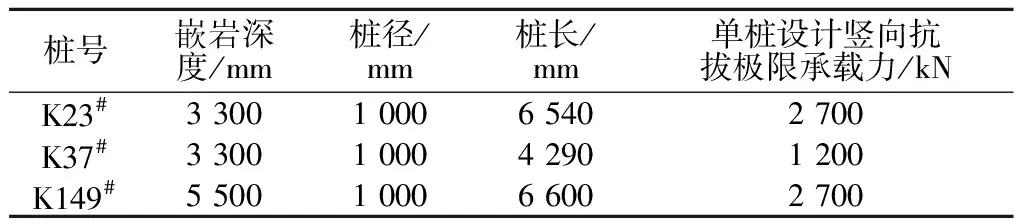
表2 试验桩基本参数Table 2 Basic parameters of test piles

为检测抗拔桩是否满足设计要求，采用自平衡试验方法对表2中3根基桩进行抗拔试验，以确定抗拔桩的承载力特征值是否满足工程要求。

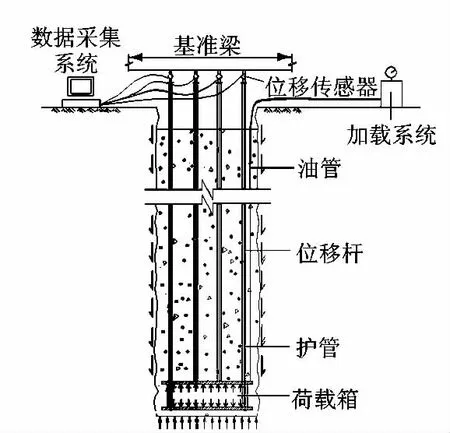
图1 自平衡测试原理Fig.1 Schematic of self-balancing test

2.2 试验原理及方法

试验采用“基桩自平衡法”对指定检测的抗拔桩进行抗拔试验[12]。成桩前预先埋设荷载箱，并在荷载箱顶、底盖上安装上、下位移计，位移计位于位移杆内部，其原理及构造见图1。荷载箱中的压力可用压力表测得，上下盖板的位移可用位移传感器测得。根据抗拔桩的上拔位移绘制的δ-U曲线(δ为上拔位移，U为抗拔桩竖向承载力)即可确定试验桩承载力特征值，具体试验过程方法参见规程[12]和《建筑基桩检测技术规范》(JGJ 106—2014)[13]。

2.3 试验结果及分析

对现场试验数据进行整理可绘制出图2所示的δ-U曲线，在加载过程中3根桩均未达到极限状态且δ-U曲线均属于“陡变型”。图中O—A1、O—A2、O—A3为加载段；A1—C1、A2—C2、A3—C3为卸载段。

根据《建筑地基基础设计规范》(GB 50007—2011)[14]附录T单桩竖向抗拔荷载试验要点T.0.10第1条规定：对于陡变型曲线，取相应于陡升段起点荷载值；同时，根据T.0.1第一条规定，将单桩竖向抗拔极限承载力除以2得到单桩竖向抗拔极限承载力特征值。由《建筑地基基础设计规范》(GB 50007—2011)和图2可得K37#、K23#、K149#的承载力特征值分别为2 715.8，5 596，5 594.5 kN，均满足设计要求。

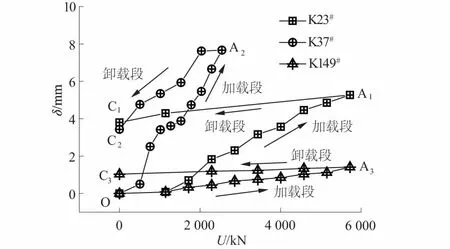
图2 试验δ-U曲线Fig.2 Curves of δ-U(load-settlement) obtained from test

3 数值模型确定嵌岩抗拔桩极限承载力

为进一步研究嵌岩抗拔桩桩侧阻力、桩身轴力、各桩的极限承载力及不同嵌岩深度对抗拔极限承载力影响的承载特性，根据工程实测的岩土参数，结合中风化岩层的实际情况，选取适合的参数，建立合理的FLAC3D数值模型，运用所建模型分别对土体中的3根嵌岩抗拔桩K37#、K23#、K149#进行数值模拟分析，确定其极限承载力。同时，以K23#桩的参数及地质条件建模，分析了桩的埋深与桩身轴力、桩侧阻力的影响，以及桩径D、嵌岩深度h对极限承载力Pu的影响，具体过程如下。

3.1 模型建立及参数的确定

3.1.1 基本假定

利用弹塑性力学知识，假定地基为一个半无限体，忽略次要因素影响，可作以下基本假设[15]：

(1)桩、岩体为均质、连续体，且各向同性。

(2)孔壁粗糙，桩岩接触面为非理想界面咬合接触。

(3)由于嵌岩桩嵌固段承载特征突出，视桩底为悬空。

(4)桩身为弹性体，岩体为理想弹塑体，岩体本构模型符合摩尔-库仑准则。

(5)不考虑时间效应，荷载为静力荷载。

3.1.2 基本参数

该工程场地各土(岩)层参数见表3。其他各参数中岩石变形模量Es=342.30 MPa，弹性模量E=16.304 GPa，泊松比ν=0.21；土体弹性模量E=4 MPa,泊松比ν=0.18。

表3 场地土层参数Table 3 Soil parameters on site

根据式(1)、式(2)可得岩石体积模量K=9.37×109Pa， 剪切模量G=1.41×109Pa，但由于试验区的岩石为中风化岩石，岩石较为破碎，故该2个指标作为模型值过大，不能代表中风化岩石的力学性质，需对岩石的体积模量及剪切模量折减到1/10左右，故模型使用的岩石体积模量K=9.37×108Pa， 剪切模量G=1.41×108Pa；土体体积模量K=2.99×106Pa， 剪切模量G=1.653×106Pa。

(1)

(2)

式中：E为岩土的变形模量；ν为材料的泊松比。

根据孙书伟等[16]编著的《FLAC3D在岩土工程中的应用》可知：①接触面的内摩擦角φ和黏聚力c一般为接触面周围材料的0.6～0.7倍，本文取0.7倍；②接触面的切向刚度Ks和法向刚度Kn取为接触面相邻区域材料的“最硬”处材料等效刚度的10倍，即

(3)

式中：K为岩土材料体积模量； ΔZmin为接触面上连接区域上的最小尺寸。

但当材料的黏聚力和内摩擦角已知时，接触面的法向刚度和切向刚度的值要通过试验数据反演，对3根桩进行数值模拟可最终确定土体接触面的切向刚度Ks和法向刚度Kn均为5.19×108Pa,岩石切向刚度Ks和法向刚度Kn均为2.621×1012Pa；土层的内摩擦角φ=7°，黏聚力c=5 600 Pa；岩石的内摩擦角φ=21.7°，黏聚力c=25 200 Pa。

3.1.3 数值模型

本文采用FLAC3D对嵌岩桩进行模拟分析，根据地质条件，利用桩体轴向受荷的对称性，嵌岩桩模型采用 1/2 半无限体模型且模型按土(岩)体模型、桩体模型(桩长与实际桩长相同)与接触面单元模型组合建立(见图3)，其相关参数见表3。

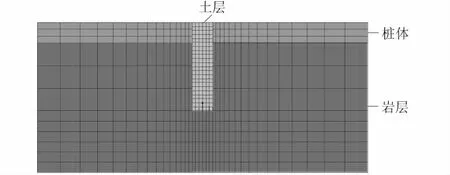
图3 桩整体网格图Fig.3 Global grids of pile

模型节点数为3 813，单元数为3 168。模型截面尺寸为16 m×8m；模型深度方向的尺寸为桩长+3 m厚岩石长度。约束情况：地面为自由面；桩周桩土(岩)为对称约束；桩身底部为荷载施加位置。

3.2 数值模拟成果与分析

3.2.1 试验桩数值模拟及极限承载力的确定

运用FLAC3D软件数值模拟自平衡分级加载试验时，数值模拟与现场试验步骤一致，数值模拟结果与试验数据对比情况见图4，可以看出数值模拟数据与试验数据δ-U曲线变化趋势一致且值的大小相近，说明所建模型可模拟该工程现场情况。

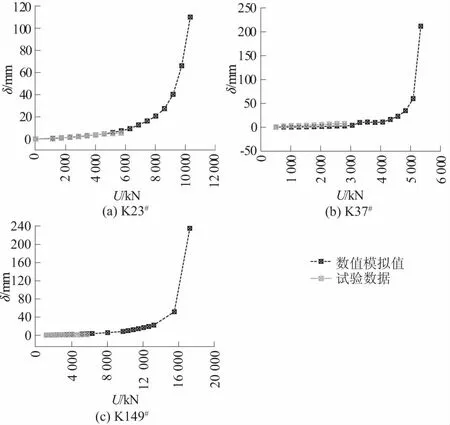
图4 模型桩δ-U曲线Fig.4 Curves of δ-U of model pile

根据《建筑地基基础设计规范》(GB 50007—2011)，由数值模拟δ-U曲线可得到扣除抗拔桩自重后的极限承载力见表4。

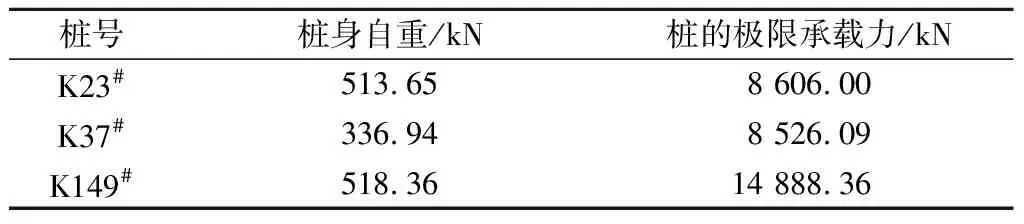
表4 试验桩极限承载力Table 4 Ultimate bearing capacity of each test pile

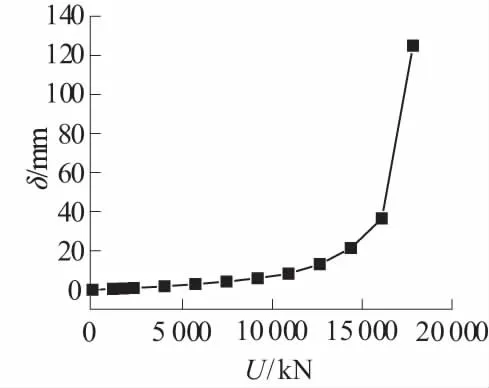
图5 完全嵌岩抗拔桩 δ-U曲线Fig.5 Curve of δ-U completely socketed uplift pile in rock

3.2.2 不同嵌岩深度下桩的抗拔特性研究

以K23#桩的岩土参

数为条件，分别对嵌岩深度h为0，2，3.3，4.5，6.54 m及桩径D为1.0，1.2，1.4，1.6，1.8 m的抗拔桩进行数值模拟分析，分析得到完全嵌岩抗拔桩的δ-U曲线见图5，在不同嵌岩深度h及不同桩径D下抗拔桩的极限承载力变化规律见图6。

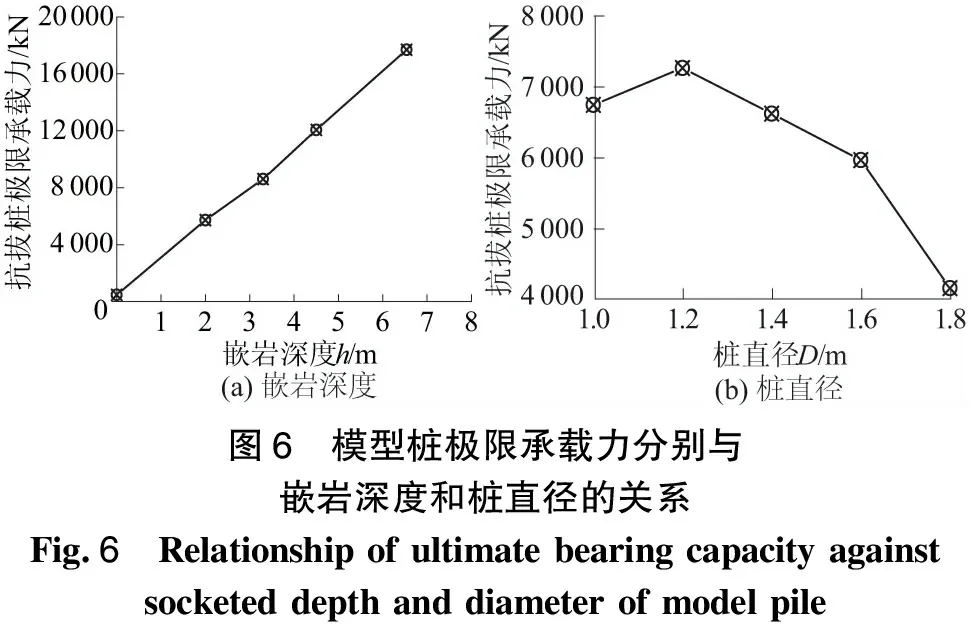
图6 模型桩极限承载力分别与嵌岩深度和桩直径的关系Fig.6 Relationship of ultimate bearing capacity againstsocketed depth and diameter of model pile

从图6(a)可看出，随着嵌岩深度的增加，抗拔桩的极限承载力显著增强，在嵌岩深度2～3 m范围内其承载力增大幅度不大，但嵌岩深度3～6.54 m范围，抗拔桩的极限承载力增大较快，这表明在设计嵌岩抗拔桩时，一般要求嵌岩深度>3 m为宜，且嵌岩深度越大越好，当嵌岩深度h=0 m时，其极限承载力为82 kN，当嵌岩深度为h=6.54 m时，极限承载力为17 700.4 kN，说明嵌岩抗拔桩的极限承载力受嵌岩深度h的影响较大。

从图6(b)可以看出，随着桩径的增加，抗拔桩的极限承载力先增大后减小。当桩径在1.0～1.2 m范围内时，极限承载力与桩径正相关，但在1.2～1.8 m这个范围内时，极限承载力与桩径负相关，说明抗拔桩的极限承载力具有尺寸效应。

3.2.3 嵌岩抗拔桩桩身轴力及桩侧阻力的变化

根据数据模拟分析结果，可得到模型桩在不同级别荷载下的桩身轴力见图7。

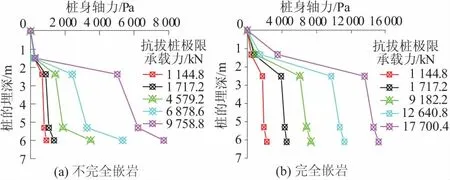
图7 模型桩轴力分布曲线Fig.7 Curves of axial force distribution of model piles

从图7可以看出，桩身轴力随桩埋置深度的增大而变大。当抗拔桩抗拔承载力增大时，桩身轴力随之增大，且在一定范围内，存在以下规律，即桩身轴力在埋深0～3 m范围内变化较大，在3～6.54 m范围内变化较小，且不同嵌岩深度的变化规律存在显著差异。

根据桩身轴力与极限侧摩阻力的关系，桩侧阻力可以按公式(4)计算[17]

qsik=(Qi-Qi+1)/ΔAs。

(4)

式中：Qi为第i截面轴力;Qi+1为第i+1 截面轴力;ΔAs为桩身第i段的侧面积，ΔAs=πd·ΔLi,其中d为桩身直径,ΔLi为桩身第i段的长度。

根据式(4)可计算得到K23#桩在不同嵌岩情况和不同级别荷载下桩侧阻力随桩埋置深度分布曲线见图8。

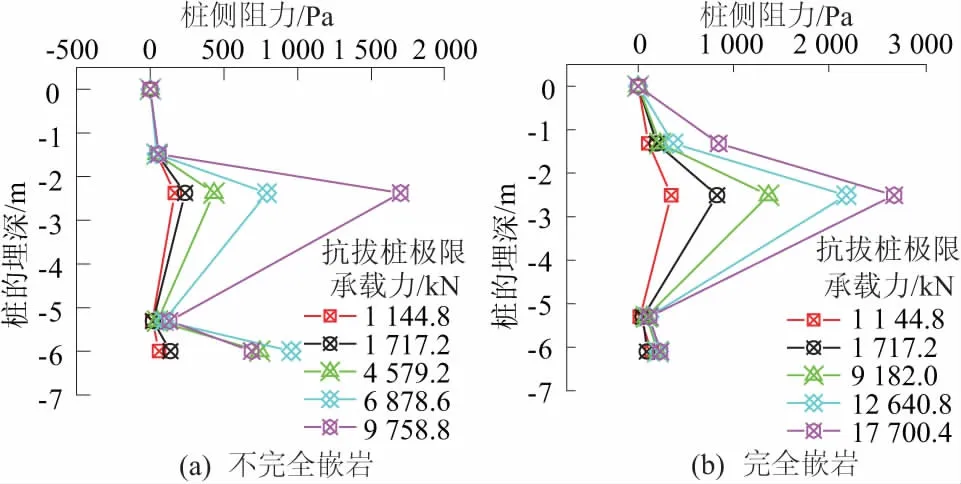
图8 模型桩侧阻力分布曲线Fig.8 Curves of side resistance distribution of model piles

由图8可知，嵌岩桩桩侧阻力的分布规律与文献[1]相似。桩侧阻力随向上荷载的增加而增加。模型桩不完全嵌岩时，在加载过程中产生的侧阻力主要分布在桩身上部区域，在荷载为9 758.8 kN时，侧阻力最大值为1 698.57 Pa, 位置接近于模型上部桩长1/3处，其下部产生的侧阻力相对较小；模型桩完全嵌岩时，在加载过程中产生的侧阻力主要分布在桩身中部区域，在荷载为17 700.4 kN时，侧阻力最大值为2 685.98 Pa, 位置接近于模型上部桩长1/2处。其下部产生的侧阻力也相对较小。

值得注意的是，尽管模型桩在建立时，假定桩/岩(土)接触面光滑，没有明显的沟槽或台阶，但是桩在不完全嵌岩或者完全嵌岩情况下，侧阻力分布明显不均匀，其上部、中部产生的侧阻力远大于下部、桩身两端的侧阻力。即在嵌岩深度相同时，作用的荷载越大，其轴力越大，从而相应的桩侧阻力越大；随着埋置深度的增加，桩侧阻力先增大后减小，桩中间的桩侧阻力最大，因此，桩中部的侧阻力对极限抗拔承载力贡献最大。

4 结 论

(1)本文对中风化泥质白云岩地质条件下的嵌岩抗拔工程桩进行了“自平衡”抗拔试验，根据试验结果，可知该工程桩满足设计要求。

(2)在中风化泥质白云岩的地质条件下，嵌岩抗拔桩数值模型建立时，风化岩石的参数剪切模量G、体积模量K一般取为试验换算值的1/10左右。

(3)嵌岩抗拔桩的极限承载力Pu与其嵌岩深度h及桩身直径D关系密切。对6.54 m长的嵌岩抗拔桩数值模拟表明：Pu随h的增加而增大，Pu随D的增大先增大后减小。在嵌岩深度2～3 m范围内其Pu增大幅度不大，但嵌岩深度3～6.45 m范围，Pu增大较快，因此，在抗拔桩的设计时，其嵌岩深度h不宜太小，h>3 m为宜;在D<1.2 m范围内，桩径的增加对Pu是有利的；在D>1.2 m的范围内，桩径的增加对Pu是不利的；说明抗拔桩极限承载力具有尺寸效应。

(4)在桩长范围内，桩身轴力随嵌岩深度的增加而增大，且增加幅度受桩周岩土体的影响，在桩端底部达到最大值。

(5)桩侧阻力不是均匀分布的。随埋置深度的增加，桩侧阻力先增大后减小，桩中部的桩侧阻力最大，且桩中部的侧阻力对极限抗拔承载力贡献最大。