砂岩地基上地下结构浮力特性研究
2019-03-18,,,,,
,,,, ,
(1.兰州大学 西部灾害与环境力学教育部重点实验室,兰州 730000; 2.兰州大学 土木工程与力学学院,兰州 730000; 3.青岛勘察测绘研究院,山东 青岛 266011
1 研究背景
目前,随着工程建设的发展,城市用地减少,人地矛盾突出,城市建筑开始向地下空间发展[1-3],大埋深地下室、地下车库涌现。地下结构的底板往往低于地下水位,结构设计必须考虑抗浮性能。抗浮设计多利用阿基米德定律计算结构浮力,亦即采用静水压力[4-5]。此基底浮力计算方法存在较大争议,部分学者认为建筑物浮托力由孔隙水压力引起,并不等于静水压力[6],且伴随着渗流过程发生,与地基土的渗透系数、渗流条件、渗透压及渗透时间密切相关[7],实际浮力应根据土-水-基础系统的相互作用对静水条件下的全水头压力进行折减;相反,也有学者认为不论地基渗透性如何,在高渗透压、长时间作用下,基底的浮力最终都会接近全水头压力,不宜折减[8-9]。
针对地下结构的抗浮问题争议,早期工程师们的经验结论与研究者的试验成果相互结合,形成了规范的条文规定。《岩土工程勘察规范》(GB 50021—2017)[10]规定:对基础、地下结构物和挡土墙,应考虑在最不利组合情况下地下水对结构物的上浮作用,原则上按设计水位计算浮力,对节理不发育的岩石和黏土且有地方经验或实测数据时,可根据经验确定;《岩土工程手册》[11]规定:当建筑物位于粉土、砂土、碎石土和节理裂隙发育的岩石地基时,按设计水位100%计算浮托力。当建筑物位于节理裂隙不发育的岩石地基时,按设计水位50%计算浮托力。当建筑物位于黏性土地基时,其浮托力较难确定,应结合地区的实际经验考虑; 《给水排水工程构筑物设计规范》(GB 50069—2016)[12]规定:地表水或地下水对结构作用的浮托力,其标准值应按最高水位确定,并应按qw=γwhwηfw计算,其中ηfw为浮托力折减系数。可以看出,规范对浮托力的计算规定不一,实际中很难去界定所属类型。鉴于此,后来许多学者进行了更加详细的研究,宋林辉等[13]模拟了黏土层上的深基础,将实测中的浮力与阿基米德定律计算的理论浮力进行了对比,得到了水压力折减系数为0.65左右;孙广利等[14]结合工程实际,利用孔隙水压力计对粉质黏土地基进行了观测,得到折减系数为0.85。宋林辉等[8-9]以黏土为地基,进行了模型试验,测试结果显示,黏土地基水压可以折减,折减原因有2点:一是水头损失;二是土颗粒与基底有接触,减少了水与基底的接触面积。张第轩等[15-16]通过室内模型试验,指出砂土和黏土地基均不可折减。以上成果从不同领域的结构设计角度出发,依地基土类型、结构进行分类,结论对地库抗浮设计意义非凡,但是也存在着诸多问题。例如规范界定模糊,不易操作,而且不同规范对同一内容的规定有所差异;研究主要集中在砂土、黏性土地基上,对黏性土地基的水压折减观点不一,出现不折减或多种折减系数的结论;对同一地基没有考虑地下水的渗流条件影响,这也是分析认为以往研究中黏性土地基出现多种结论的主要原因。
本文针对目前深基坑地下结构广泛触及的砂岩地基,通过设计室内模型试验研究渗流条件、渗透压、渗流时间对地下结构浮力特性的影响,同时依托兰州某砂岩地基地下车库工程,进行现场基底孔隙水压力监测试验,验证模型试验结果,以期得到一些有用的结论,为此类工程抗浮设计提供依据。
2 模型试验
2.1 试验原理
静水中任一点处于球应力状态,浮力按阿基米德定律计算,即
F浮1=ρgΔV1=ρgAΔh1。
(1)
式中:ρ为液体密度(kg/m3);g为重力加速度(m/s2);A为水压作用面积(m2);ΔV1为排开液体的体积(m3);Δh1为静水头高度差(m)。
位于地基上的地库底板,其浮力由地下水经渗流后的孔隙水压力引起,水头差有所损失,实际基底浮力为
F浮2=ρgΔV2=ρgAΔh2。
(2)
式中:ΔV2为等效排开液体的体积(m3);Δh2为实际浮力作用等效水头(m)。定义抗浮折减系数为
(3)
试验测定模型所受浮力并转化成折减系数进行分析。
2.2 试验设备
原则上需选择量程小、精度高的土压力盒与孔隙水压力计进行试验,但受模型试验操作空间、砂岩自身性质(坚硬且平整度差)的限制,选用直接测量仪器埋设困难、误差大。因此选用间接测量方法设计试验,主要设备包括:用于模拟边界的试验箱(800 mm×800 mm×1 500 mm),用于模拟建筑物的模型箱(400 mm×400 mm×600 mm),测量浮力变化的S型拉压称重传感器(CFBLSM)或电子秤,控制加水量和监测水位变化的水位标。此外还包括钢横梁、螺母、螺杆、垫板、水龙头、水桶、卷尺、水平尺等设备。
2.3 试验过程
2.3.1 悬吊法试验过程
采用2种试验方法进行,分别是悬吊法和预压法。悬吊法如图1(a)所示,试验箱底部中央设置处理平整的模拟地基,地基与试验箱侧壁间空隙用标准砂回填,模型箱模拟建筑物,置于地基上,用螺杆将模型箱、电子秤、支撑于试验箱上的刚性横梁连接,试验开始前调节螺纹套筒使电子秤读数为模型箱及箱内砂土质量之和,静置一段时间后重新校正电子秤读数,开始稳定平缓地向试验箱内预注一定水量饱和地基,待地基饱和不再吸水后开始试验注水,每次注水高2 cm,记录水位随时间的变化,直到水头不再下降后开始下一次注水,试验终止条件为相邻2次注水电子秤读数不再变化(模型箱已浮起)。

图1 悬吊法示意图及其受力情况Fig.1 Schematic diagram and force analysis of suspension method
悬吊法中模型箱的受力情况如图1(b)所示,主要有拉力F1、重力G、浮力F浮、地基土的支持力p,液体对试验箱侧壁的黏滞力f。静力平衡条件为
F1+F浮+pA1=G+fA2。
(4)
式中:A1为支撑力p的作用面积;A2为黏滞力f的作用面积。
黏滞力f忽略不计,初始状态已调节电子秤读数为G,故支持力p为0,于是有
F浮=G-F1。
(5)
2.3.2 预压法试验过程
预压法如图2(a)所示,与悬吊法的不同之处在于:用螺纹钢筋连接拉压称重传感器和刚性横梁,试验开始前调节上下螺母施加1 N的压力(尽量小)在模型箱上,传感器读数突变时停止试验注水,此时的水位即为上浮水位。
预压法中模型箱受力如图2(b)所示,主要有预压力F2、重力G、浮力F浮、地基土的支持力p,液体对试验箱侧壁的黏滞力f。静力平衡条件为
F浮+pA1=G+F2+fA2。
(6)

图2 预压法示意图及其受力情况Fig.2 Schematic diagram and force analysis of preloading method
同样黏滞力f忽略不计,预压力F2已知,影响可以忽略,随着水头的增加,浮力首先克服重力G,支持力p变小,F2保持不变;当模型箱有上浮趋势时,支持力减小到0,F2突变,F浮=G,比较注水高度与F浮等效高度得η。
悬吊法的优点是能在模型试验中反映渗透压、时间的变化过程对浮力的影响,但是基底与地基间的作用力很小,并不等于结构物的重力,与实际情况有所差别,这一影响因素造成的是系统误差,并不影响整体规律。预压法与实际情况更接近,但只能得到最终的起浮水位,不能反映过程变化量,故设置2种试验方法相互结合修正,以期得到科学的试验结论。2种方法均进行渗流条件、渗透压、渗透时间的影响研究。渗流条件设置3种常见工况:基底与地基接触处不做处理(条件1);基底与地基接触处封闭但地基内部有裂隙(条件2);基底与地基接触处封闭且地基内无裂隙(条件3)。其中封闭措施采用快凝水泥沿四周接触部位外侧呈90°焊缝状密封,密封条带薄、抗拉强度低且破坏易出现在胶结面上,可忽略密封连接强度对浮力的影响。地基材料选用混凝土(模拟完全不透水材料)、砂岩、粉土、卵石(完全透水材料)。
3 试验结果分析
3.1 悬吊法
3.1.1 不透水材料
3种渗流条件下不透水材料地基上基础模型浮力、折减系数与渗透压(加水深度)的关系见图3。

图3 不透水材料浮力和折减系数随注水高度的 变化曲线Fig.3 Variations of buoyancy and reduction coefficient of impervious material against water injection height
由图3可以看出:
条件1时,基础所受浮力与理论值接近,随渗透压增加近似线性增长,折减系数趋于稳定,不随渗透压发生变化,其值在0.86~0.96之间。原因在于混凝土虽然属于不透水材料,但此时地下水主要通过基底与地基间的接触缝隙渗入基底,不透水地基的隔水作用难以有效发挥,故水压力折减较小。
条件2(制作模型时预先支模留设裂隙)时,基础所受浮力与理论值偏差较大,随着渗透压的增加,折减系数先增大后趋于稳定,其值在0.63~0.73之间。不透水地基发挥了一定的隔水作用,但地基内裂隙的存在提供了渗流通道,并且随着渗透压的增大,通过裂隙到达基底的地下水增加,原来的部分地基-基础接触面积不断被渗水薄膜侵占[17-18],这种侵占作用虽然随着渗透压的增大而增大,但也有一定的限度,因此折减系数呈现先增大后稳定的变化趋势。
条件3时,基础所受浮力与理论值偏差最大,折减系数在小渗透压下快速增长,随后趋于稳定,其值为0.22~0.46,不透水地基的隔水作用得以有效发挥,地下水主要通过地基材料的孔隙渗透进入基底。
水压力的折减主要发生在条件2、条件3两种情况下,为了研究渗流时间与所受浮力的关系,选取2种情况下理论起浮渗透压时浮力随时间的变化分析,如图4。

图4 不同条件下的浮力随时间变化曲线Fig.4 Buoyancy-time curves under different conditions
由图4(a)可知,随着时间的推移,条件2时,基础所受浮力逐渐增大,浮力增加速率逐渐减小,原因在于地基与基底间的接触点情况不一,通过裂隙渗入基底的水膜,最先侵占大部分容易渗入的接触点,随后才慢慢随着时间的增加形成对较难侵入点的占据,最后达到稳定;由图4(b)可知, 条件3时,基础所受浮力不随时间变化。
3.1.2 砂岩地基
用砂岩块代替不透水材料地基进行试验,其中通过挖取天然条件下完整程度不同的砂岩块模拟有裂隙、无裂隙工况。同理可得基础所受浮力、折减系数与渗透压(加水深度)的变化曲线如图5所示。

图5 砂岩地基浮力和折减系数变化随注水高度的 变化曲线Fig.5 Variations of buoyancy and reduction coefficient of sandstone foundation against water injection height
由图5可以看出,砂岩地基与不透水材料地基的浮力-渗透压关系曲线基本相同,砂岩在地库抗浮设计中可当作不透水材料对待。其水压力折减系数与不透水材料地基的取值范围大体相同,但随着渗透压的变化规律有所不同。3种渗流条件下,注水起始阶段,折减系数均出现突增现象,主要原因在于砂岩预饱和后,附着的部分土性黏结物膨胀剥落,填充在内部裂隙、孔隙及表面坑洼处,自然状态下的部分渗流通道在小渗透压下阻塞,只有当渗透压稍有增加时,填充物被带走,渗流通道恢复至自然状态,浮力增加明显。条件1、条件2时,折减系数在初始阶段突增之后,变化趋势与不透水材料情况下相似,取值分别为0.82~0.91,0.56~0.73;条件3时,折减系数为0.31~0.47,其随渗透压的增加而波动上升,升幅较小,原因在于砂岩地基内部的孔隙随着渗透压的增加逐渐贯通,连通的孔隙形成了新的渗水通道,通道内砂岩微粒易在高渗透压的作用下不断被渗流水份带走,通道扩张,这在此砂岩的渗透系数试验、微观试验中可以得到证实[19];砂岩地基上基础浮力随时间的变化与不透水材料相似,这里不予赘述。
3.2 预压法
预压法除对砂岩地基进行试验外,还对粉土(夹杂黏粒)、卵石地基进行了研究,模型试验结果如图6所示。

图6 模型基础起浮水位Fig.6 Floating water level of base model
对于3种地基材料:卵石、粉土、砂岩,起浮水位依次增大(理论起浮水位为16 cm)。对于砂岩地基的3种渗流条件,起浮水位也依次增大。卵石情况下,折减系数接近于1,为完全透水层,不能进行折减;粉土情况下,折减系数0.86,和文献[14]的研究成果0.85基本吻合;砂岩地基上条件1、条件2时,折减系数分别为0.86,0.70,在悬吊法结果的范围之内,更接近范围上限。条件3时,折减系数为0.50,超出悬吊法的结果范围,但是相差不大,与文献[11]的结论一致。悬吊法与预压法相比,折减系数偏小,水浮力折减过大,建议实际中按照情况采用接近所给范围上限的折减系数。
综合考虑2种相互补充的试验结果,认为砂岩地基上的地下结构抗浮设计可以考虑浮力折减。当基底与地基接触处不作处理时,折减系数为0.82~0.91;当基底与地基接触处采取封闭措施但地基内有裂隙时,折减系数为0.63~0.73;当基底与地基接触处封闭且砂岩地基内部无裂隙时,折减系数为0.31~0.50。实际工程中要充分发挥砂岩的隔水作用,必须在基底和地基接触面四周作封水处理,改变渗流路径,增大水头损失,使地下水通过渗流进入基底,而不是通过基底与地基间的缝隙进入,保证折减合理充分。这也是规范中要求基坑肥槽回填时必须在靠近建筑物周围1 m范围内利用2∶8灰土进行回填并保证密实度的原因所在。基底浮力具有时间效应,渗透压对其影响也较大,必须在实际工程中加以动态考虑,不能单纯地以某一时间点的某一水头来衡量建筑整个使用过程中的抗浮性能。
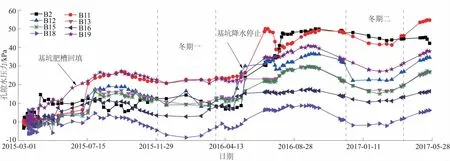
图8 孔隙水压力随时间变化曲线Fig.8 Curves of pore water pressure against time
4 现场监测
本文依托的兰州某地下车库工程,砂岩地基,筏板基础,主楼32层,裙楼2层,3层地下车库,如图7所示,地下水流向自东向西,在参照点1和参照点2处水位较高,超过基础底板10.3 m。地库东侧紧临另一建成使用的地下结构,无地下水流出。抗浮设计时考虑浮力折减,为保证抗浮设计安全,同时验证折减的合理性,进行基底水压力监测试验辅助降水措施。孔隙水压力计平面布置见图7(取车库的一半),地库边缘及中心均有布置,测点编号为B2,B8,B11,B12,B13,B14,B15,B16,B18,B19,其中测点B8,B14埋设后因施工原因失效。按就近影响的原则,水位最高处参照点1和参照点2的影响区以南北中线划分, B11,B12,B13,B16,B18,B19属参照点1影响范围,B2,B15属参照点2影响范围,各测点距参照点的距离见表1(横向为东西方向)。监测时间从2015年3月到至2017年5月。
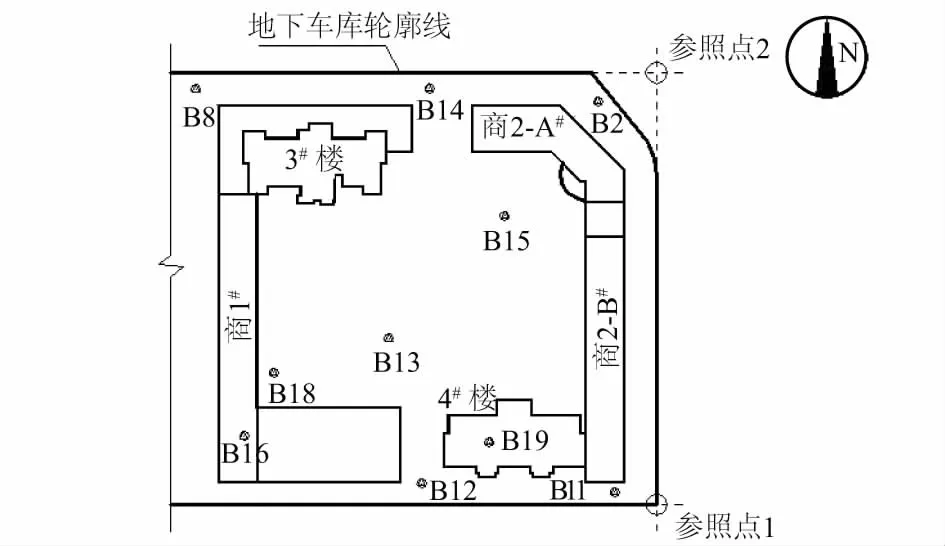
图7 孔隙水压力计平面布置Fig.7 Plane layout of pore water pressure gauges
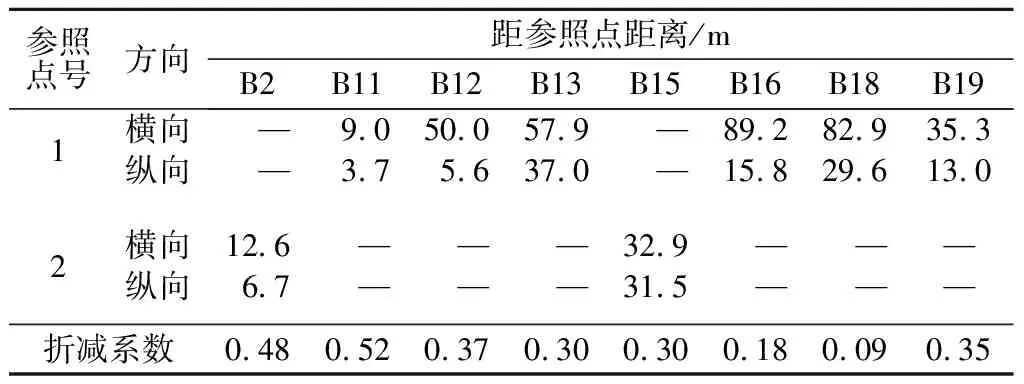
参照点号方向距参照点距离/mB2B11B12B13B15B16B18B1912横向纵向横向纵向折减系数—9.050.057.9—89.282.935.3—3.75.637.0—15.829.613.012.6———32.9———6.7———31.5———0.480.520.370.300.300.180.090.35
基坑开挖时在肥槽边设置有排水沟,集中抽水保证地下水位稳定不影响施工,排水沟低于筏板底面标高。各测点孔隙水压力如图8所示,监测初期,各测点孔压值经过一段时间波动后趋于稳定,均在10 kPa以内;整个监测期内,孔压曲线出现2处上升台阶、2处低谷,均是渗透压变化的结果。2处上升分别在基坑肥槽回填后、基坑外围降水井停止降水后;肥槽回填,槽底1 m高度范围内采用素混凝土封堵,水压难以释放,渗透压增大;停止降水后,地下水位回升,渗透压亦增大。2处低谷均位于冬季贫水期,地下水位较丰水期稍有下降,渗透压降低;孔压第2次上升稳定后,各测点数值相当于10.3 m的渗透压在基底与地基接触处封闭条件下的渗流结果,其大小与测点位置的渗透压和渗流路径长短相关。因地下水位沿基坑长边方向变化,测点渗透压与横向位置相关,渗流路径按基坑短边方向考虑,渗流路径与纵向位置相关。B1,B2分别与参照点1、参照点2距离最近且位置对称,孔压值均处于最高水平;B13与B12 相比,渗透压接近,受渗流路径较长影响而孔压值较低;B16,B18横向距离远大于其他测点,主要受渗透压的影响,孔压值最小;B19在整个时期内均处于较高位置,孔压值2次爬升时间段较其他测点稍长,主要因为此处岩块较为破碎,砂岩孔隙渗流贯通扩张明显,渗透系数变化大所致。
利用各点2次上升稳定后的孔压值,计算基础底板实际浮力作用水头并换算为折减系数,结果见表1。其值处于0.30~0.52之间(B16,B18除外),与此渗流条件下模型试验的结果较为吻合,且上述现场试验针对渗透压、渗流路径对水压力的影响研究与模型试验所得规律一致,说明模型试验所得结论可以推广到实际情况,为地库抗浮设计提供依据。
5 结 论
本文自行设计模型试验,结合现场试验监测数据,探究了砂岩地基渗透机理,可以得到如下结论:
(1)渗流条件对浮力折减影响最大。基底与地基接触处不做处理时,地下水通过基底与砂岩地基间缝隙进入基底,折减系数取0.82~0.91;基底与地基接触处做封闭处理但砂岩内部有裂隙时,地下水主要通过裂隙进入基底,折减系数取0.63~0.73;基底与地基接触处封闭且地基内无裂隙存在时,地下水通过砂岩内部孔隙渗透进入基底,折减系数取0.31~0.50。改变地下水渗流条件对水压力折减系数影响较大,基坑肥槽回填时易在基底四周做封水处理,减小抗浮设计要求。
(2)渗透压、渗透时间对浮力的影响随渗流条件而变。基底与地基接触处做封闭处理但砂岩内部有裂隙时,渗透压、渗透时间变化使基底与地基接触面积因水膜侵占而发生变化,二者对基础所受浮力影响较大;基底与地基接触处封闭且地基内无裂隙存在时,渗透压可以改变砂岩孔隙的存在状态,对基础所受浮力有所影响但效果较小,渗透时间对其基本没有影响;基底与地基接触处不做处理时,渗透压、渗流时间并不能造成地基发生实质性变化,对基础所受浮力影响最小,可以不加考虑。
(3)在渗流条件相同的情况下,单从水理性质来说,砂岩与混凝土相似,属不透水材料,但混凝土微观结构稳定,孔隙发生渗流侵蚀不易,较砂岩而讲其抗浮折减系数变化范围较小。
(4)实际中地库抗浮设计十分复杂,采用静水位计算并不合理,应综合地基材料渗透性、渗流条件、渗透压、渗透时间等因素经方案论证后综合决定。
