边界非完整约束悬臂裂纹梁的静力参数识别
2019-03-18杨骁,孟哲,黄瑾
杨 骁, 孟 哲, 黄 瑾
(上海大学土木工程系, 上海200444)
由于梁中的裂纹和梁柔性边界的刚度对梁的动静力学行为有显著影响[1-4], 因此梁边界条件和裂纹损伤程度的正确描述是合理分析梁动静力响应的前提. 同时, 梁边界条件及其裂纹的识别也是检测梁结构损伤的主要内容之一[5-11], 通常梁构件的边界和裂纹损伤识别可分为基于振动的动力识别方法[5-6,8-9,12-18]和基于静态变形的静力识别方法[7,10-11,19-25]. 虽然基于振动的动力识别方法已具有完备的理论基础, 并获得了丰富的研究成果和应用成果, 但是相关研究表明, 在某些情况下动力识别方法并不能提供精确的损伤信息[26]. 对于简单结构而言, 静力损伤识别不仅方便易行, 而且还可以有效地避免惯性和阻尼的不确定性对损伤识别结果的影响, 故建立可靠便捷的基于静力响应的梁损伤识别方法成为近年来的研究热点.
目前, 已有学者将梁裂纹等效为线性扭转弹簧实现裂纹的静力损伤识别. Buda等[20]建立了基于裂纹梁测量挠度与其显式闭合通解之差最小的优化算法, 给出了Euler-Bernoulli 梁裂纹位置及其损伤程度的识别方法, 并考察了挠度测量噪声对裂纹损伤识别的影响; Caddemi等[19,21]利用梁裂纹诱导挠度函数, 通过非线性方程求解, 给出了在已知裂纹大致位置及数量情况下单(多)裂纹的损伤识别方法; Yazdanpanah等[22]利用有限元法给出了梁裂纹定位的计算方法, 但该方法未涉及裂纹损伤程度的确定. 另外, 类似于裂纹诱导挠度函数, Sun等[27]基于基线修正建立了悬臂型结构的损伤识别方法; Koo等[10]利用梁裂纹诱导弦挠度函数, 建立了在正弯矩检测载荷条件下裂纹位置的确定方法; 而汪德江等[23]给出了Timoshenko 梁开闭裂纹位置及损伤的识别方法. 近年来, Wang等[7]给出了基于静力挠度的楔形悬臂梁边界竖向和扭转支承刚度的3 种识别方法, 并研究了识别刚度对测量挠度的敏感性; Wang等[11]进一步将该方法推广至具有内部竖向支承楔形悬臂梁支承刚度的识别. 然而,由于识别方法中涉及病态矩阵方程的求解, 故其应用范围受到一定的限制; 同时, 作者尚未见到相关的能同时确定梁构件边界弹性支承刚度和裂纹损伤程度的静力识别方法.
本工作给出了边界非完整约束悬臂裂纹梁的参数识别方法, 其步骤如下: 首先, 将悬臂梁中开裂纹等效为内部扭转弹簧, 而其边界非完整竖向和扭转约束分别等效为竖向弹簧和扭转弹簧, 并利用Delta 函数和Heaviside 函数得到了边界弹性支承悬臂Euler-Bernoulli 裂纹梁静力弯曲的显式闭合通解; 其次, 利用损伤诱导挠度函数给出了边界支承柔度的计算公式, 证明了其损伤诱导挠度函数和裂纹诱导弦挠度函数是分段线性函数, 其斜率在裂纹处发生突变, 且斜率改变量依赖于该处裂纹的等效扭转弹簧柔度, 从而建立了裂纹等效扭转弹簧柔度的计算公式, 避免了通常损伤识别方法中易出现的非线性方程组求解较难和解的非唯一性问题; 最后, 通过具有1 条和2 条裂纹的边界非完整约束悬臂裂纹梁的参数识别, 数值验证了本方法的适用性和可靠性, 并对挠度测量噪声和裂纹深度等对识别结果的影响进行了考察.
1 边界非完整约束悬臂裂纹梁弯曲的诱导挠度
图1 为边界非完整约束悬臂裂纹梁示意图. 图中, 设横截面长和高分别为L 和h 的矩形截面边界非完整约束悬臂Euler-Bernoulli 梁在x = xi(i = 1,2,···,N)处存在深度为di的开裂纹, 且其抗弯刚度为(E I)0. 将边界非完整约束等效为刚度分别为Kd和Kr的竖向弹簧和扭转弹簧, 且将裂纹i(i=1,2,···,N)等效为刚度为Ki的扭转弹簧[28], 其中

于是, 裂纹梁的等效抗弯刚度(E I)e可表示为[29-31]
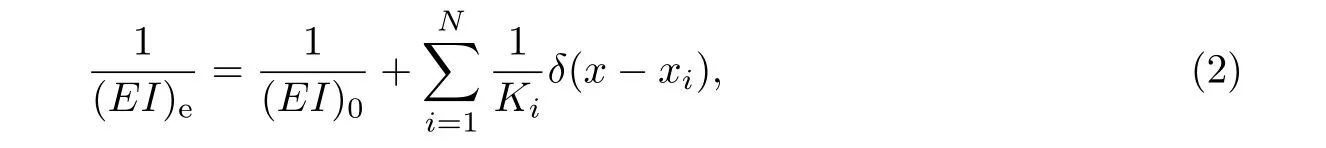
式中, δ(x)=H′(x)为Delta 函数, H(x)为Heaviside 函数[23,29].
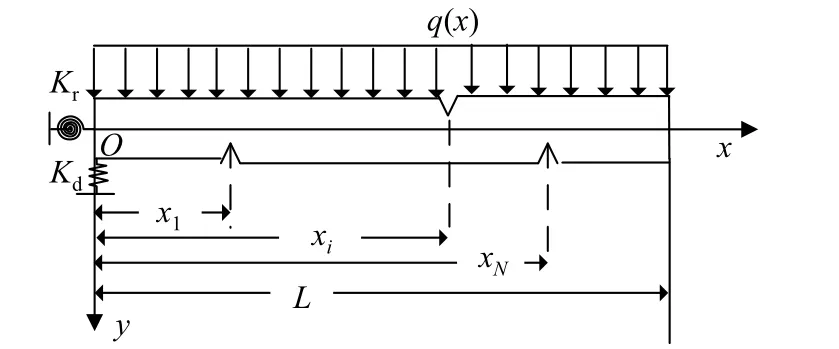
图1 边界非完整约束悬臂裂纹梁Fig.1 Cantilever cracked beam with nonholonomic constraint boundary
在横向载荷q(x)的作用下, 边界弹性支承悬臂裂纹梁静力弯曲的边值问题为

式中, w(x)为裂纹梁的挠度, M 和FS分别为裂纹梁的弯矩和剪力, 且

引入如下无量纲量和参数
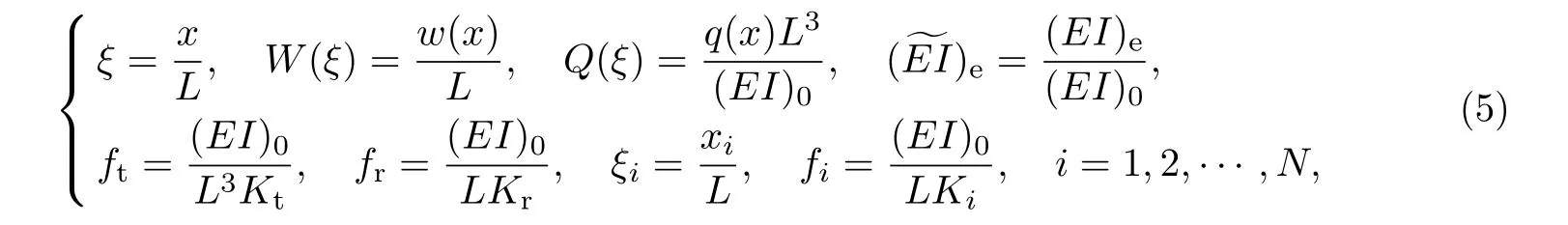

那么边值问题(式(3))的无量纲形式为

利用Delta 函数δ(ξ)和Heaviside 函数H(ξ)的性质, 可得边值问题式(7)的解为
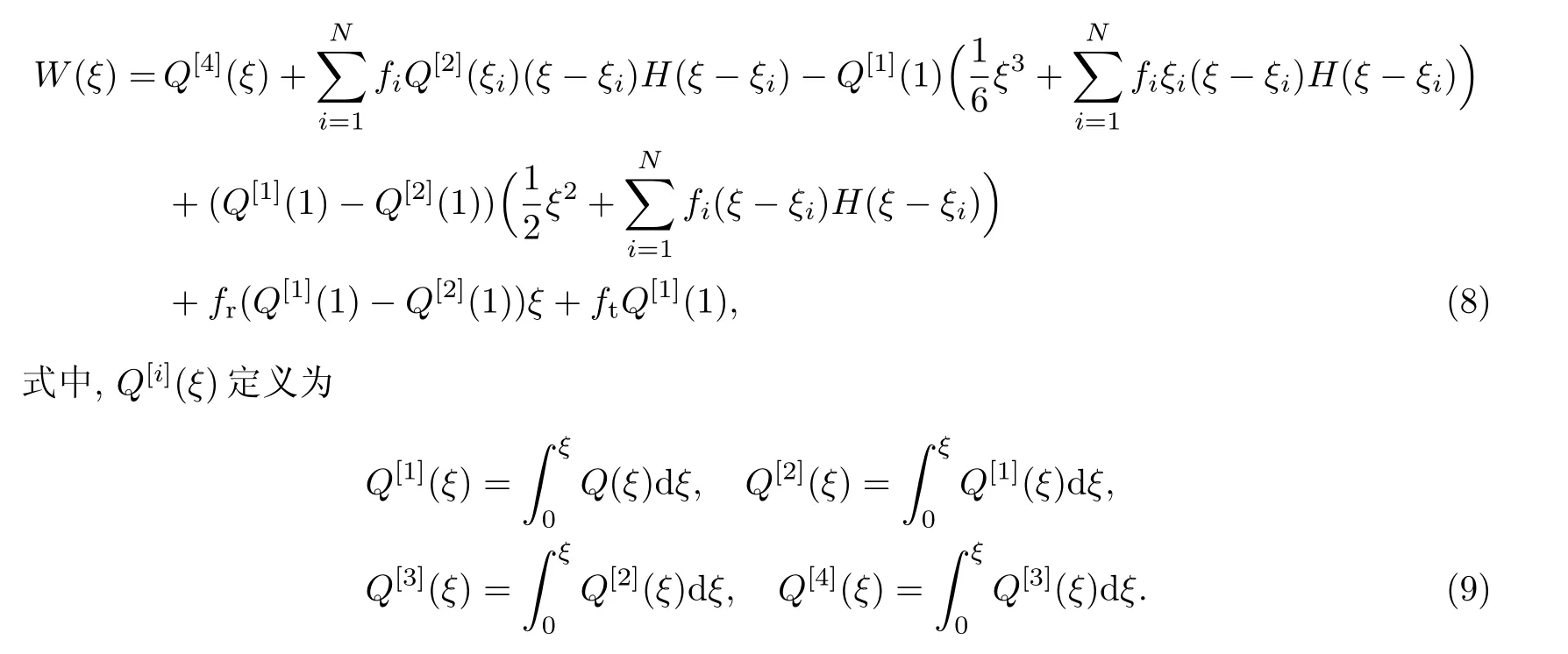
而无量纲弯矩m(ξ)和剪力fS(ξ)分别为

对于边界完整固定约束的无裂纹悬臂梁, 即fr= fS= 0, fi= 0(i = 1,2,···,N), 其无量纲挠度为
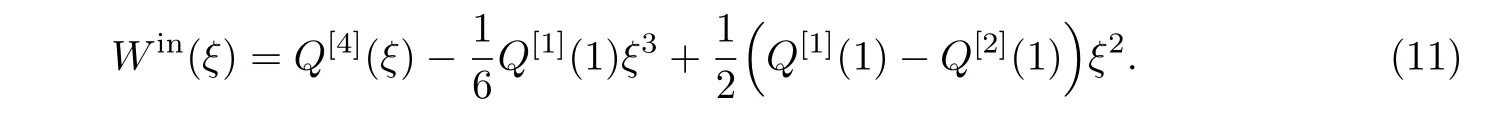
边界非完整约束以及裂纹引起的损伤诱导挠度函数WD(ξ)定义为
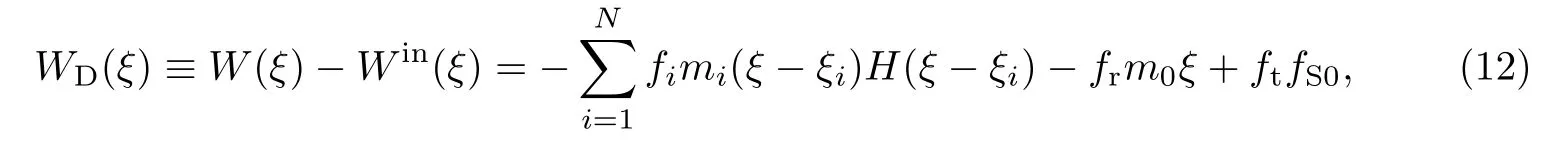
式中, fS0和m0分别为梁支承边界处的无量纲弯矩和剪力, 而mi为裂纹i(i = 1,2,···,N)处的无量纲弯矩, 且

为了依次识别裂纹损伤, 定义区间[ξa, ξb]上的裂纹诱导弦挠度函数

于是, 如果梁在区间[ξa, ξb]中存在l 条裂纹, 分别位于ξ =ξi(i=i0+1, i0+2,··· ,i0+l)处,则由式(12)可得

可见, 损伤诱导挠度函数WD(ξ)和裂纹诱导弦挠度函数WC(ξ)是分段线性函数, 即为折直线. 当区间[ξa, ξb]中不存在裂纹时, 损伤诱导挠度WD(ξ)为直线, 而裂纹诱导弦挠度函数WC(ξ)≡0; 当区间[ξa, ξb]中存在l 条裂纹, 且mi0 (i=i0+1, i0+2,··· ,i0+l)时, 裂纹诱导弦挠度函数WC(ξ)由l+1 条直线段组成.
2 边界非完整约束柔度及裂纹损伤程度的识别
在边界非完整约束端ξ = 0 附近选取2 个位置ξe1和ξe2, 满足0 < ξe1< ξe2< ξ1< ξ2<··· < ξN< 1, 即区间[0, ξe2]中不存在裂纹. 如果ξ = ξe1和ξ = ξe2处挠度测量值分别为和则有

这样, 完成了边界非完整约束悬臂裂纹梁边界支承柔度fr和ft的识别.
对于裂纹的损伤识别, 选取区间[ξa, ξb], 使得区间[ξa, ξb]中只存在一条裂纹i = j0,此时选取β > 0, 且令= ξa+ β,= ξb−β, 使得如果和处的挠度测量值分别为和, 则式(12)和(14)可得

则由式(18)可得

至此, 完成了区间[ξa, ξb]中裂纹j0的位置ξj0和裂纹损伤程度fj0的识别.
事实上, 如果区间[ξa, ξb]中存在多条裂纹, 则可以将区间[ξa, ξb]分为2 个子区间, 如等分为2 个子区间[ξa, (ξa+ξb)/2]和[(ξa+ξb)/2, ξb], 并根据裂纹诱导弦挠度函数(ξ)的性质判断这2 个子区间中是否存在裂纹, 如此下去, 可得到若干子区间, 使每个子区间中只存在一条裂纹.
可见, 不同于通常同时确定所有参数的损伤识别方法[12,16-17,20-24], 本工作基于损伤诱导挠度和裂纹诱导弦挠度的参数识别方法, 通过不同区间的选取, 依次逐个识别待定参数, 从而避免了非线性方程组的求解和参数识别反问题中解的非唯一性问题.
3 数值算例
假定边界非完整约束悬臂裂纹梁承受均布载荷的作用, 即Q(ξ)=Q0, 则
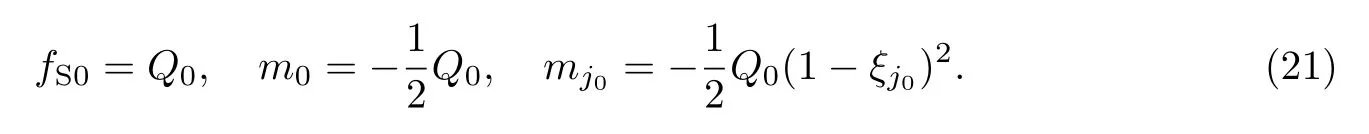
作为数值试验, 考虑测量噪声的影响, ξ 处挠度的测量值可由精确挠度W(ξ)近似为

式中, e 为测量误差, 而R()为[−1, 1]中的均匀分布随机数.
3.1 具有一条裂纹的边界非完整约束悬臂梁参数识别
作为第一个数值例子, 首先假定边界非完整约束悬臂裂纹梁在ξ1= 0.5 处存在深度为d1的裂纹, 并设ft= fr= 0.05, 取Q0= 1. 图2 为在不同裂纹深度d1下, 边界非完整约束悬臂裂纹梁的无量纲挠度W(ξ)和无量纲损伤诱导挠度WD(ξ)沿无量纲坐标ξ 的分布; 图3 显示了在区间[ξa, ξb]分别为[0, 1]和[0.3, 0.7]时, 无量纲裂纹诱导弦挠度WC(ξ)沿无量纲坐标ξ 的分布. 从图中可见, 相比于损伤诱导挠度WD(ξ)和裂纹诱导弦挠度WC(ξ)函数, 边界非完整约束悬臂裂纹梁无量纲挠度W(ξ)的裂纹效应并不明显. 对于无裂纹梁(d1= 0), 其无量纲损伤诱导挠度WD(ξ)为直线; 对于裂纹梁(d1̸=0), 无量纲损伤诱导挠度WD(ξ)和裂纹诱导弦挠度WC(ξ)均为由2 条线段构成的分段线性函数, 且2 条线段交点的横坐标即为裂纹位置.另外, 随着裂纹深度的增大, 裂纹位置处斜率的改变量也增大, 同时边界支承附近无量纲损伤诱导挠度WD(ξ)的直线段斜率为m0fr, 与纵坐标轴的截距为ftfS0.
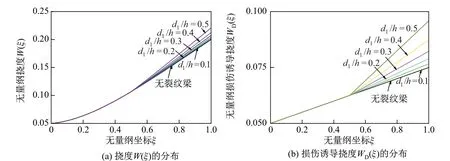
图2 当ξ1 = 0.5 时, 不同裂纹深度d1/h 下边界非完整约束裂纹梁挠度W(ξ)和损伤诱导挠度W D(ξ)的分布Fig.2 Distributions of the defections W(ξ) and damage-induced deflections W D(ξ) of the cantilever cracked beam with nonholonomic constraint boundary for different crack depths d1/h when ξ1 =0.5
取ξe1= 0.1 和ξe2= 0.3, 表1 给出了当无量纲柔度fr= ft分别为0.01, 0.03 以及0.05 时,不 同 测 量 误 差e 下, 由 式(17)确 定 的 边 界 近 似 柔 度分 别 与 其 精 确 值fr和ft的 误差er和et, 其中误差定义为

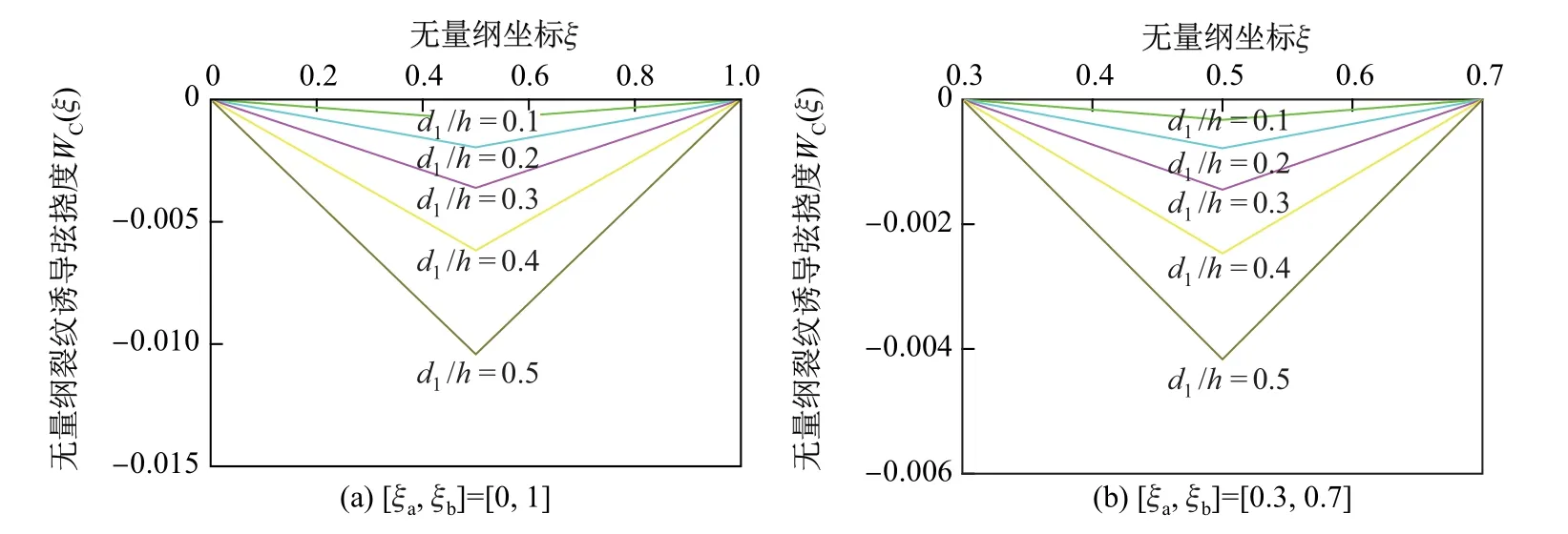
图3 当ξ1 =0.5 时, 不同裂纹深度d1/h 下边界非完整约束裂纹梁裂纹诱导弦挠度W C(ξ)的分布Fig.3 Distributions of the crack-induced chord-wise deflections W C(ξ)of the cantilever cracked beam with nonholonomic constraint boundary for different crack depths d1/h when ξ1 =0.5
可见, 当测量误差e 较小时, 式(17)可给出柔度fr和ft的较精确识别结果和而随着测量误差e 的增大, 柔度fr和ft的识别误差迅速增大, 且误差er大于误差et. 同时, 计算发现误差er和et随着ξe2−ξe1的减小而增大, 其原因是由式(16)确定式(17)的系数矩阵病态[7,11],因此如要获得柔度fr和ft的较精确识别结果, 应严格控制挠度和的测量误差, 并尽可能地使ξe2−ξe1增大.
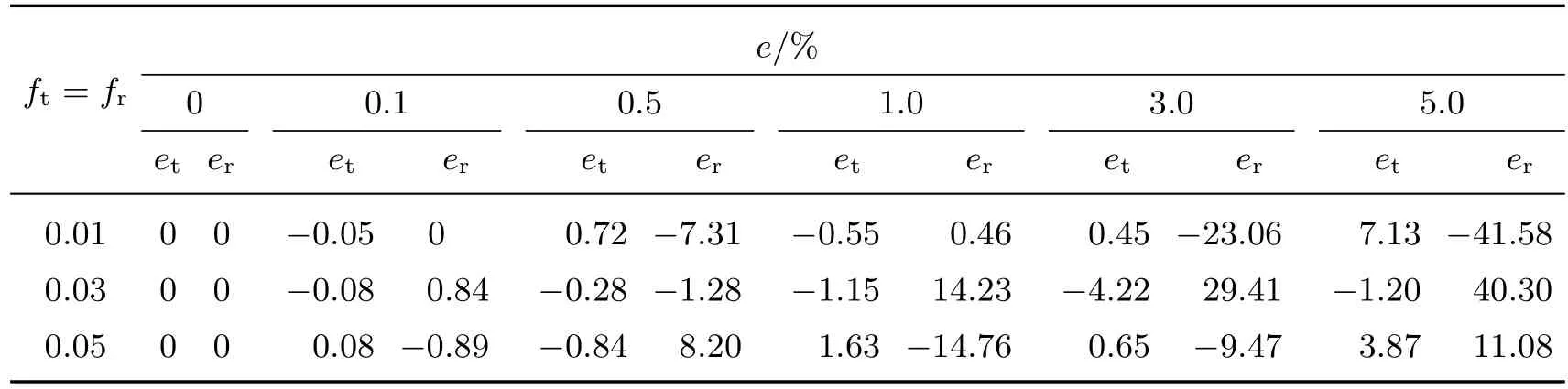
表1 不同测量误差e 下边界非完整约束柔度f r 和f t 的识别结果Table1 Identification results of the nonholonomic constraint compliances f r and f t for different measurement errors e
表2 给出了在不同裂纹深度d1和不同测量误差e 下, 由式(20)确定的裂纹近似位置及其等效弹簧近似柔度分别与其精确值ξ1和f1的误差eloc1和ef1(取ξa=0.3,ξb=0.7 和β =0.1), 其中误差eloc1和ef1分别为
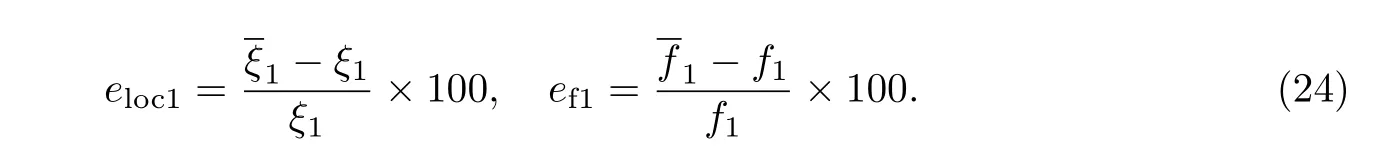
可见, 随着测量误差e 的增大, ξ1和f1的识别误差总体增大, 但当测量误差e �5%时, 由式(20)可给出较精确的ξ1和f1的识别结果. 同时计算发现, 参数β 的选取对识别结果几乎没有影响.
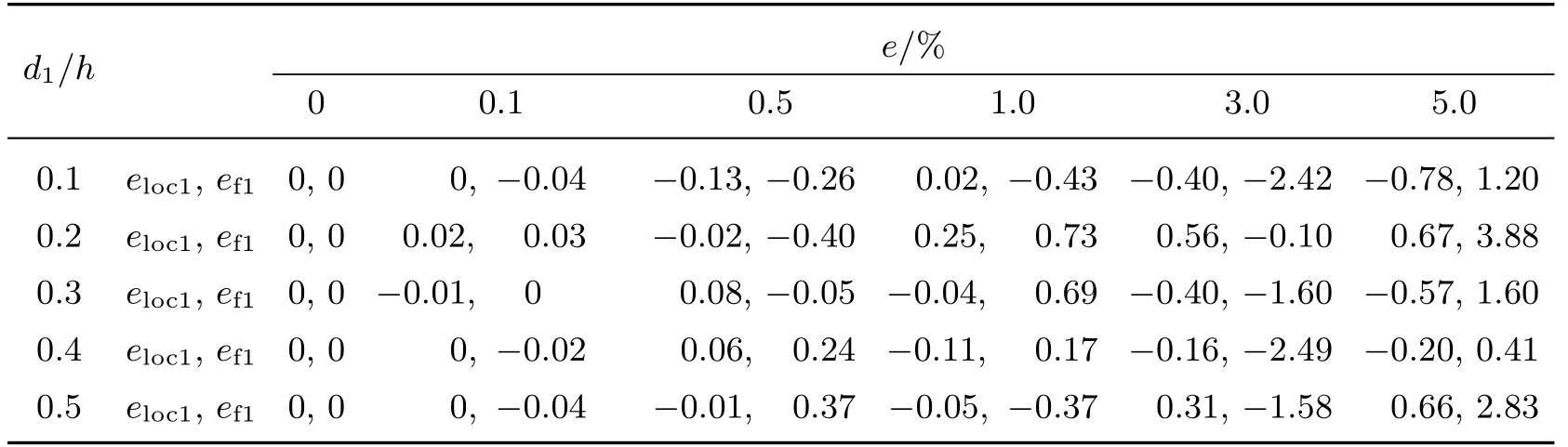
表2 不同裂纹深度d1/h 和测量误差e 下裂纹位置ξ1 及裂纹等效弹性柔度f1 的识别结果Table2 Identification results of the crack locations ξ1 and compliances f1 of the crack equivalent spring with different crack depths d1/h and measurement errors e
3.2 具有2 条裂纹的边界非完整约束悬臂梁参数识别
设边界非完整约束悬臂裂纹梁在ξ1= 0.4 和ξ2= 0.7 处存在深度分别为d1和d2的裂纹,这时仍取Q0= 1, ft= fr= 0.05. 图4 给出了在不同裂纹深度d = d1= d2下, 边界非完整约束悬臂裂纹梁的无量纲挠度W(ξ)和无量纲损伤诱导挠度WD(ξ)沿无量纲坐标ξ 的分布.从图中可以看出, 相比WD(ξ), W(ξ)的裂纹效应不明显, 并且对于2 条裂纹梁而言, WD(ξ)为由3 条线段构成的分段线性函数, 其交点即为裂纹位置, 分别为ξ1=0.4 和ξ2=0.7.
图5 给出了区间[ξa, ξb]分别为[0.2, 0.6]和[0.5, 0.9]、无测量误差e = 0 和测量误差e = 1%时, 无量纲裂纹诱导弦挠度WC(ξ)沿无量纲坐标ξ 的分布. 从图中可以看出, 当区间[ξa, ξb]只含1 条裂纹时, 其裂纹诱导弦挠度WC(ξ)为2 条线段组成的分段线性函数, 且随着裂纹深度的增大, 裂纹位置处斜率的改变量增大.

图4 当ξ1 =0.4, ξ2 =0.7 时, 不同裂纹深度d/h 下具有2 条裂纹边界非完整约束梁挠度W(ξ)和损伤诱导挠度W D(ξ)的分布Fig.4 Distributions of the defections W(ξ) and damage-induced deflections W D(ξ) of the cantilever beam with nonholonomic constraint boundary and two cracks at ξ1 = 0.4 and ξ2 =0.7 for different crack depths d/h
取ξa= 0.2, ξb= 0.7 和β = 0.1, 表3 给出了在不同裂纹深度d = d1= d2和不同测量误差e 下, 由式(20)确定的裂纹ξ1= 0.4 的近似位置及其等效弹簧近似柔度分别与其精确值ξ1和f1的误差eloc1和ef1. 表4 给出了当ξa= 0.5, ξb= 0.9 和β = 0.1, 不同裂纹深度d = d1= d2和不同测量误差e 下, 裂纹ξ2= 0.7 的近似位置及其等效弹簧近似柔度分别与其精确值ξ2和f2的误差eloc2和ef2, 其中误差eloci和efi(i = 1,2)的定义为eloci=−ξi)/ξi, efi=−fi)/fi(i = 1,2). 由表3 和4 可见, 随着测量误差e 的增大, 裂纹位置ξi和裂纹等效弹簧柔度fi(i = 1,2)的识别误差总体增大. 但整体而言, 利用裂纹诱导弦挠度可给出较精确的裂纹位置和裂纹等效弹簧柔度的识别结果, 因此本工作建立的边界非完整约束悬臂裂纹梁边界弹性支承柔度和裂纹位置及其等效扭转弹簧柔度识别方法具有一定的适用性和可靠性.
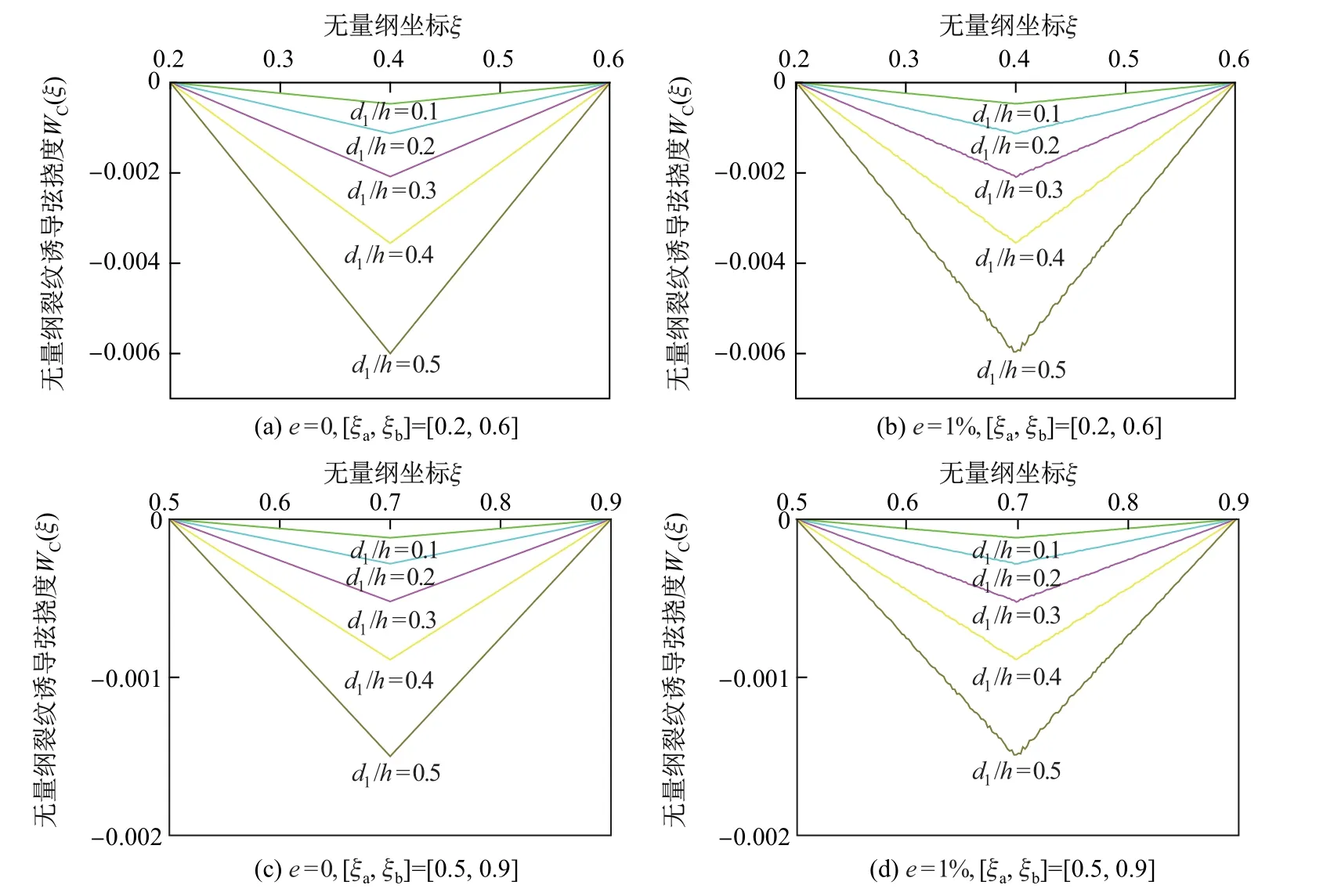
图5 当ξ1 = 0.4, ξ2 = 0.7 时, 不同裂纹深度d/h 下具有2 条裂纹边界非完整约束梁裂纹诱导弦挠度W C(ξ)的分布Fig.5 Distributions of the crack-induced chord-wise deflections W C(ξ) of the cantilever beam with nonholonomic constraint boundary and two cracks at ξ1 = 0.4 and ξ2 = 0.7 for different crack depths d/h
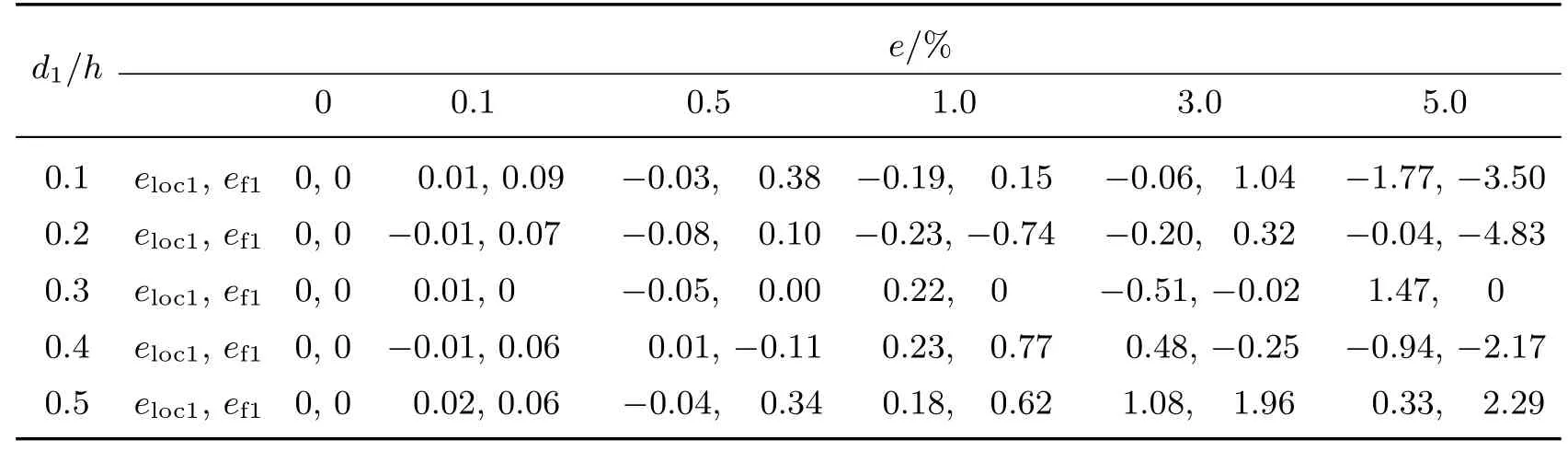
表3 不同裂纹深度d1/h 和测量误差e 下裂纹位置ξ1 及裂纹等效弹性柔度f1 的识别结果Table3 Identification results of the crack locations ξ1 and compliances f1 of the crack equivalent spring with different crack depths d1/h and measurement errors e

表4 不同裂纹深度d2/h 和测量误差e 下裂纹位置ξ2 及裂纹等效弹性柔度f2 的识别结果Table4 Identification results of the crack locations ξ2 and compliances f2 of the crack equivalent spring with different crack depths d2/h and measurement errors e
4 结 论
本工作对边界非完整约束悬臂裂纹梁的边界弹性支承柔度和裂纹损伤的静力识别方法进行了研究. 首先, 给出了弹性支承悬臂Euler-Bernoulli 裂纹梁静力弯曲的显式闭合通解; 其次,基于损伤诱导挠度和裂纹诱导弦挠度的性质, 给出了边界支承柔度和裂纹位置及其等效扭转弹簧柔度的识别方法, 该方法可依次逐个识别待定参数, 避免了通常损伤识别方法中由于同时识别若干参数所导致的算法复杂和解的非唯一性问题; 最后, 考虑挠度的测量噪声, 数值验证了本工作所建立的悬臂裂纹梁边界支承柔度及裂纹损伤识别方法的适用性和可靠性, 考察了裂纹深度和位置等对识别结果的影响, 得到如下结论:
(1) 由于涉及到病态矩阵, 基于损伤诱导挠度的边界支承柔度识别误差较大, 故为获得较精确的识别结果, 应严格控制挠度的测量误差, 并且尽量使2 个挠度测量点相距较远;
(2) 基于裂纹诱导弦挠度的裂纹位置和裂纹损伤程度识别方法具有可靠的精度, 且裂纹深度和位置对其识别结果影响较小;
(3) 随着挠度测量误差增大, 裂纹位置和裂纹等效扭转弹簧柔度识别误差总体增大, 但识别结果仍具有较高的精度;
(4) 对于静定梁而言, 损伤诱导挠度和裂纹诱导弦挠度仍为分段线性函数, 因此本方法亦适用于识别简支梁弹性支承柔度和裂纹损伤程度.
