基于曲线拟合的降雨侵蚀力模型初探

昌霞 刘赛娥

摘  要： 城市化和工业化进程加快，由降雨所产生的城市挖填方弃土和旱坡地水力侵蚀造成的水土流失越来越不容忽视。采用云南省昆明市西山区山洪预警监测区域内的13个监测点实测得到的降雨量数据作为分析基础，充分挖掘数据信息。通过对降雨数据的进行不同的曲线拟合分析，得到幂函数曲线拟合效果最好。结合对通用水土流失方程（USLE）的理解，提出降雨侵蚀预测力模型的乘法模型。研究建立的降雨侵蚀力R值估算模型，在一定程度可以满足水土流失预测、水土保持等方面的应用需求。

关键词： 幂函数; 拟合; 降雨侵蚀力; 乘法模型

中图分类号：TP391          文献标志码：A     文章编号：1006-8228（2019）02-69-04

A preliminary study on rainfall erosion force model based on curve fitting

Chang Xia， Liu Saie

（Yunnan land and resources vocational college， Yunnan， Kunming 650000， China）

Abstract： Due to the accelerated process of urbanization and industrialization， the water and soil erosion caused by soil disposal by urban excavation and soil erosion in arid slopes is becoming more and more important. The rainfall data obtained from 13 monitoring points in the mountain flood early warning and monitoring area of Xishan District of Kunming City， Yunnan Province are used for fully mining the information. Through different curve fitting analysis of rainfall data， obtained that the power function curve fitting effect is the best. According to the understanding of the universal soil erosion equation （USLE）， a multiplication model of rainfall erosion predictive force model is proposed. The establishment of estimation model of rainfall erosion force R meets the application demand of soil erosion prediction and water and soil conservation plan.

Key words： power function; fitting; rainfall erosion force; prediction model

0 引言

降雨侵蚀力（Rainfall erosivity，简称R值）反映了降雨对土壤的潜在侵蚀能力，对降雨侵蚀力时空分布规律的研究是进行水土流失预报与监测的基础[1-2]。如何利用已知水文、气象台站的降雨数据，估算未知点的降雨侵蚀力，特别是对于台站稀少且观测点分布又极不合理的地区有着重要意义。

近年来，众多学者采用Kriging方法实现降雨侵蚀力数据的离散化和空间化，洪伟等[3]研究发现Kriging插值方法在我国降雨侵蚀力研究上有很好的拟合优度，章文波[3]利用Kriging插值方法繪制了北方农牧交错带的降雨侵蚀力等值线图，赵文武等[4]运用析取Kriging插值对延河流域降雨侵蚀力进行空间数据分析。通过“空间内插”利用特定区域已知的离散观测数据来估计规则格点上的非观测数据[3]，有效地解决了这一问题。不同的研究区域和时间尺度，适用的插值方法及模型不同，那种“包插百量”的最优内插法是不存在的。因此，根据数据与区域特征，用适宜的插值方法来确定降雨侵蚀力计算模型一直是该领域研究的要点。

1 降雨侵蚀力因子

在本节中，我们主要介绍降雨侵蚀力因子的几个较为重要的要素，及对因子分析模型中的最著名的通用水土流失方程（USLE），为后面建立降雨侵蚀力预测模型提供分析依据。

1.1 基本定义

通俗来讲，降雨侵蚀力是指降雨引起土壤侵蚀的潜在能力。由降雨引起的水土流失大致可分为两个过程：一是土粒从土体中被分离;二是分离出的土粒被冲走，雨滴降落到地表，引起土壤击溅分离，一部分雨水渗入地下，另一部分形成地表径流。美国水土保持学家维斯奇迈尔（Wischmeier）通过对各种降雨不同组合形式的土壤流失量进行相关分析，提出了降雨的动能与其30分钟最大强度的乘积是判断土壤流失的最好指标，其表达式为：

⑴

式⑴中，R表示降雨侵蚀力;E表示降雨过程中某段降雨量产生的动能;I30表示降雨过程中连续30分钟的最大降雨强度。这个方程是根据美国资料总结出来的，然而世界各地的地形、地貌、降雨分布等自然因素会极为不同，所以各地学者根据各国、各个地区的具体情况，在通用方程的基础上研究得出了许多计算R的经验公式。

1.2 R要素

不管是计算R的通用方程还是其他经验公式，都可以看到影响影响降雨侵蚀力的因素主要是降雨量、降雨强度、雨滴能量等。因为降雨量、降雨时段直接决定降雨动能。下面本文阐述下这几个影响要素对土壤侵蚀的影响及相应的临界范围。

1.2.1 降雨量

降雨量是降雨特性指标之一。在区域性降雨量级界定里，降雨量5mm以下定义为小雨，降雨量5mm～17mm定义为小到中雨，降雨量17mm～38mm定义为中到大雨，降雨量38mm～50mm定义为大到暴雨，降雨量超过50mm定义为暴雨，降雨量超过100mm定义为大暴雨，降雨量超过20mm定义为特大暴雨。统计数据表明，一般10mm以下的小雨不产生径流，也不存在侵蚀;超过10mm的中雨可能产生径流，但冲刷量很小，引起水土流失的强度不大。随着降雨量的增加，水土流失强度逐渐增大。当降雨量达到50mm时，将产生明显的水土流失，且根据雨滴能量的不同，会产生较大的径流，所以一般将降雨量=50mm作为产生明显水土流失的临界值。

1.2.2 降雨强度

降雨强度是表示降雨侵蚀力的一个重要的潜在参数，也是引起水土流失的重要因素。在一定强降雨量和时段条件下，当雨强小到一定值时，将不引起地面径流，则不易产生水土流失。据哈德逊在非洲的研究发现：当降雨强度<0.42mm/min时，土壤侵蚀作用大大降低。当雨强<0.3mm/min时，土壤侵蚀作用己经很低，而在雨滴直径较小情况下，当雨强<0.2mm/min时，就几乎难以测量到土壤侵蚀量了[3]。据中国水土保持有关专家的研究表明：一般高强度暴雨的降雨时间大多在半小时左右，即使是时间较长的一些暴雨，其雨量也往往集中在1小时或半小时左右（据统计，在此时段的降雨可占总雨量的70%）。其余时间的降雨为低强度的间歇性降雨，一般不产生水土流失[4]。由降雨侵蚀因子R的计算方程式可看出，不同时期的降雨也是影响水土流失的重要因素之一。若以年为周期，在不同月份，降雨次数、雨量大小、强度会各不相同，一般在5～9月为降雨高峰期，易引起水土流失[5]。

1.2.3 雨滴能量

雨滴自空中下落对土壤的侵蚀过程，使土壤团粒分散，将土壤颗粒溅射向各方向、搬运土壤颗粒等，这时就必然要消耗能量。土壤表面团聚体分散的可能性和团聚体的重量成负相关。所以如果由于雨滴作用而使团聚体的重量减轻，将会加速团聚体的分散、并且由地表径流输送[6]。研究表明：雨滴动能远远大于片状水流所具有的能量。在一定降雨条件下，降雨历时越短，强度越高，产生的土壤流失强度越大[7]。所以在土壤侵蚀中，降雨能量占有主要地位。

其实，降雨量、降雨强度及能量大小等因素的影响作用并不是独立的，而往往是其综合作用的结果，只是作用的程度大小不同。降雨型土壤侵蚀既可因暴雨诱发，也可由久雨产生，不可简单地受某一无明确时间概念的临界降雨量的控制，而是与总降雨量、降雨强度、降雨时间三者均有关。

1.3 通用水土流失方程USLE

USLE模型是1965年W.Wischmeier和Smith t等在对美国东部地区30个州10000多个径流小区近30年的观测资料进行系统分析的基础上提出来的，其表达式为：

⑵

式⑵中，A为土壤侵蚀模数，R为降雨径流侵蚀力因子，K为土壤可侵蚀性因子，L为坡长因子，S为坡度因子，C为植被覆盖因子，P为土壤侵蚀控制措施因子[4]。USLE模型创建之后，包括创建者在内的世界各地的研究针对应用中存在的问题进行修正。随着对土壤侵蚀机理认识的不断深入，同时也为了实现计算机技术在土壤侵蚀预报中的广泛应用，美国土壤保持局于1997年建立了USLE的修正版（RUSLE：Revised Universal Soil Loss Equation）。RUSLE的结构与USLE的结构相同，但引入了土壤侵蚀过程的概念，使各因子的含义和算法有了一定的变化：R值用正常降雨年份的降雨资料计算，L、S、C值则分别为在其他条件相同的情况下通过与标准试验区对比得出[3]。

2 降雨侵蚀力模型

使用回归分析建立降雨侵蚀力模型需要解决两个重点，一是所使用的数据是否有噪声或有无其他对分析结果产生不良影响的因素[7];二是在回歸方程求出结果后如何评价其好坏，是否达到要求。本文就昆明市西山区山洪预警监测区域内的13个监测点实测得到的降雨量数据来进行处理、建模。

2.1 原始数据分析与处理

统计得到的原始数据，在一定程度上都存在误差，有些是人为测量不准确造成的，也有观测误差，测量器械本身的误差等，这些都是无法消除的，但是测量数据量的大小可以降低这些误差[6]。在使用的原始数据还会存在缺失值，比如记录时数据损坏、无法测量等无法考虑到的因素[7]。

在使用含有缺失值的数据进行分析时，需要做缺失值处理，否则会使分析结果误差增大，一般情况下，缺失值对分析结果造成的误差会随着元数据中缺失值的比例增大而增大。处理缺失值的方法有很多，本文采取插值处理方法来对数据进行处理。对数据的分箱方法是按照降雨量、平均雨强、短时最大雨强三个自变量将数据分组，在组内对径流模数和侵蚀模数求平滑值，主要取最大值，最小值和平均值三种。这样做是为了将噪声数据处理掉，对回归分析所使用的数学模型函数收敛。

2.2 曲线拟合分析变量关系

利用曲线拟合可以分析出两个变量之间的曲线关系，由于SPSS提供的拟合曲线都是一元的，所以分别对降雨量和径流模数、平均雨强和径流模数、短时最大雨强和径流模数作曲线拟合[9]。找到近似满足的关系，在此基础上建立一个含有三个变量的数学模型。

通过对降雨侵蚀各因子对侵蚀的影响规律进行分析，可以发现径流模数和降雨量、平均雨强、短时段最大雨强都成正相关关系，即径流模数和这三个因子构成的都是增函数，所以选取的Quadratic拟合二次方程、Cubic拟合三次方程、Power拟合乘幂曲线模型、Logarithmic拟合对数方程、Exponential拟合指数方程5种增函数来进行曲线拟合。

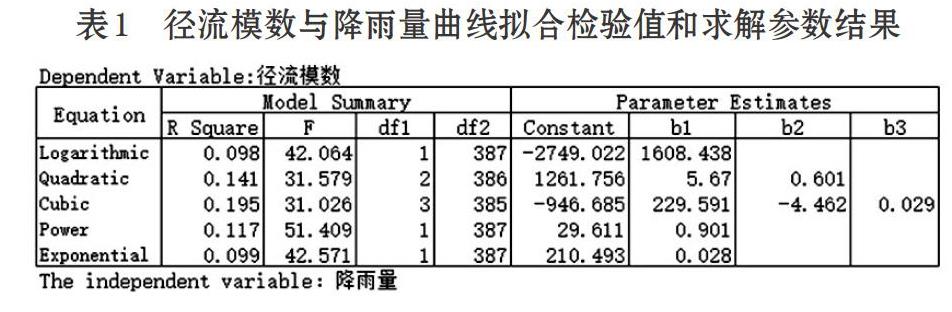
拟合采用的数据是经过预处理后的数据，径流模数使用的是经验平均值，使用SPSS软件对径流模数和三个变量进行曲线拟合，结果如下：

表1为径流模数与降雨量曲线拟合结果，相对于其他曲线，Cubic曲线拟合后计算得到的确定系数值最大，拟合效果最好。其次为Quadratic曲线和Power曲线。

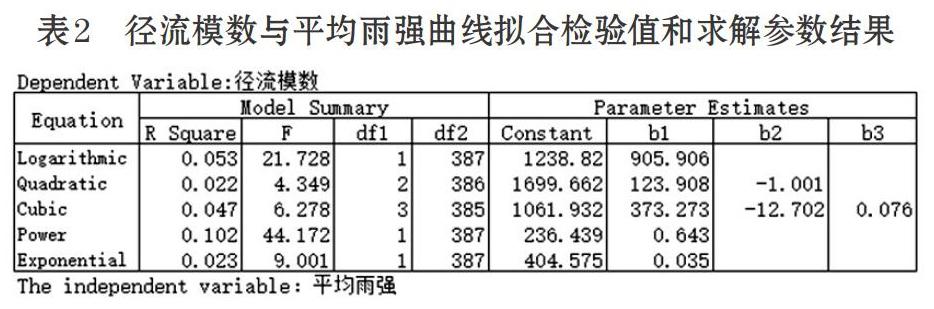
表2为径流模数与平均雨强曲线拟合结果，相对于其他曲线，Power曲线拟合后计算得到的确定系数值最大，拟合效果最好。

表3为径流模数与短时间最大雨强曲线拟合结果，相对于其他曲线，Power曲线拟合后计算得到的确定系数值最大，拟合效果最好。

2.3 乘法模型的建立

通过分析曲线拟合的结果，我们发现Power曲线对三个变量都能够较好地拟合，所以，将Power曲线模型作为基础模型，根据水土流失方程（USLE），得到各因子相乘的数学模型表达式。选取乘法模型，径流模数乘法模型为：

⑶

对式⑶进行线性化变换，即通过对数关系将各因子转换，式⑶两边通过对数变换可得：

⑷

再进行变量替换，令：

⑸

将式⑸带入式⑷，得到变换后的模型为：

⑹

这样，通过线性回归方程可以很容易求得参数值。

3 小结

本文对使用的曲线拟合进行了简单描述，给出乘法模型的构建过程。后续还需要对模型进行求解测试，分析结果。在本文中，只是选取了五个较为典型增函数来进行曲线拟合，针对不同年份、不同地区的数据可能在拟合结果上有一定差异，还需进一步扩大范围及维度。尤其在城市中，由于工程建设、施工等对土壤流失影响较大的因素的持续时间一般为2-3年，因此对应的通用土壤流失方程式中的可蚀性因子变化极快，这时只能用当年的R值进行逐年计算，才能得到较为符合实际的结果。

参考文献（References）：

[1] Shepherd J M， Burian S J. Detection of urban-inducedrainfall anomalies in a major coastal city[J]. Earth Interactions，2003.7（4）：1-17

[2] Beutel A， Faloutsos C. User behavior modeling and fraud detection[J]. IEEE Intelligent Systems，2016.31（2）：84-86

[3] Jiang B C， Yang W H， Yang C Y. An SPC-based forward-backward algorithm for arrhythmic beat detection and classification[J]. Industrial Engineeering & Management Systems， 2013.12（4）：380-388

[4] 單奇华，李卫正.俞元春.张金池.南京城市林业土壤可蚀性及影响因素[J].南京林业大学学报（自然科学版）2008.32（2）.

[5] 邹铁英.陈炼.谢泰生.数据挖掘技术在经济消费预测中的研究[J].现代计算机，2008.12.

[6] 范建荣，严冬，郭祥.GIS支持下的长江上游降雨侵蚀力时空分布特征分析[J].水土保持研究，2010.17（1）：92-96

[7] 田黎明，齐识，马金珠，等.白龙江流域上游径流年内分配变化规律分析[J].水文，2012.32（4）：82-87

[8] 孙泉忠，王朝军，赵佳等.中国降雨侵蚀力R指标研究进展[J].中国农学通报，2011.27（4）：1-5

[9] 杨轩，梁音，方继青，等.基于日降雨信息的月降雨侵蚀力模型[J].土壤学报，2010.47（2）：216-222