求解含对数势和变流动系数的Cahn-Hilliard-Hele-Shaw系统的解耦有限元方法
2019-03-16郭亚瑜贾宏恩
郭亚瑜,贾宏恩
(太原理工大学 数学学院,山西 太原 030024)
Cahn-Hilliard-Hilliard-Shaw(CH-HS)系统是数学物理中非常重要的模型。它可由在Hele-Shaw元胞中的 Cahn-Hilliard-Navier-Stokes(CH-NS)方程[1-2]简化而得,关于CH-HS的算法和背景可参考文献[3-4]。对于求解含多项式势的CH-HS系统,在文献[5]中提出了有限差分方法;在文献[6]中提出了间断Galerkin方法;在文献[7]中提出了无条件稳定的解耦方法,还有一些相关的研究可参见[8-10]。但是对于含对数势的CH-HS系统,在文献[11]中只给出了对弱解正则性的证明,并没有相应的数值方法。本文通过解耦的有限元方法,对于含变流动系数和对数势CH-HS系统的进行了相关的研究。
1 模型的建立
1.1 CH-HS模型
在Hele-Shaw元胞中的两相不可压缩流由Cahn-Hilliard-Hele-Shaw(CH-HS)方程描述:
(1)
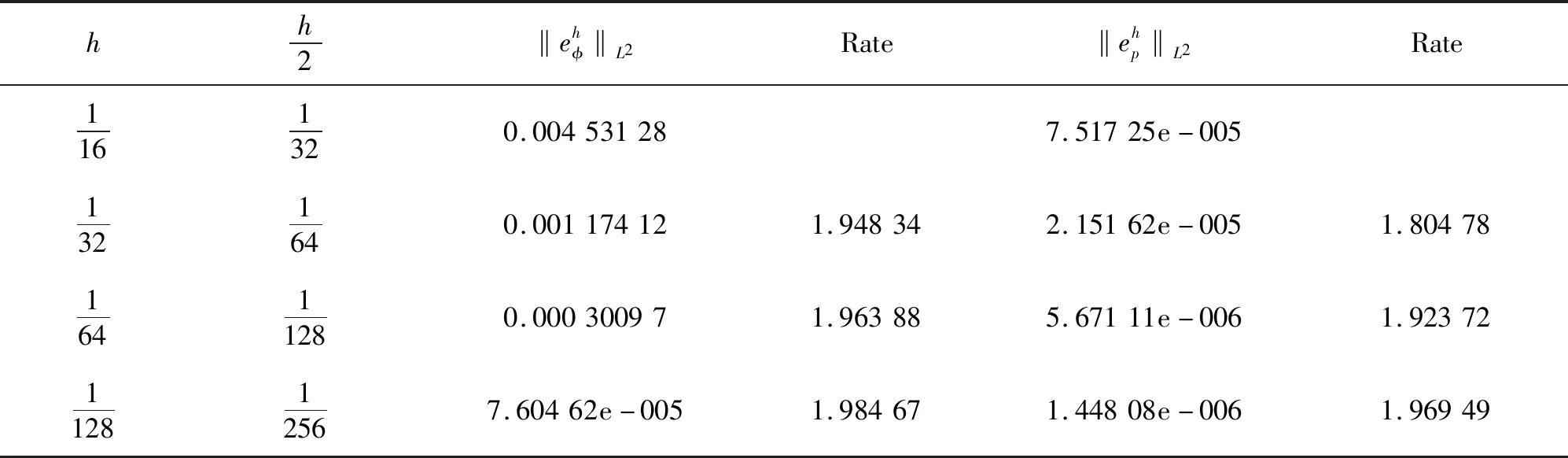
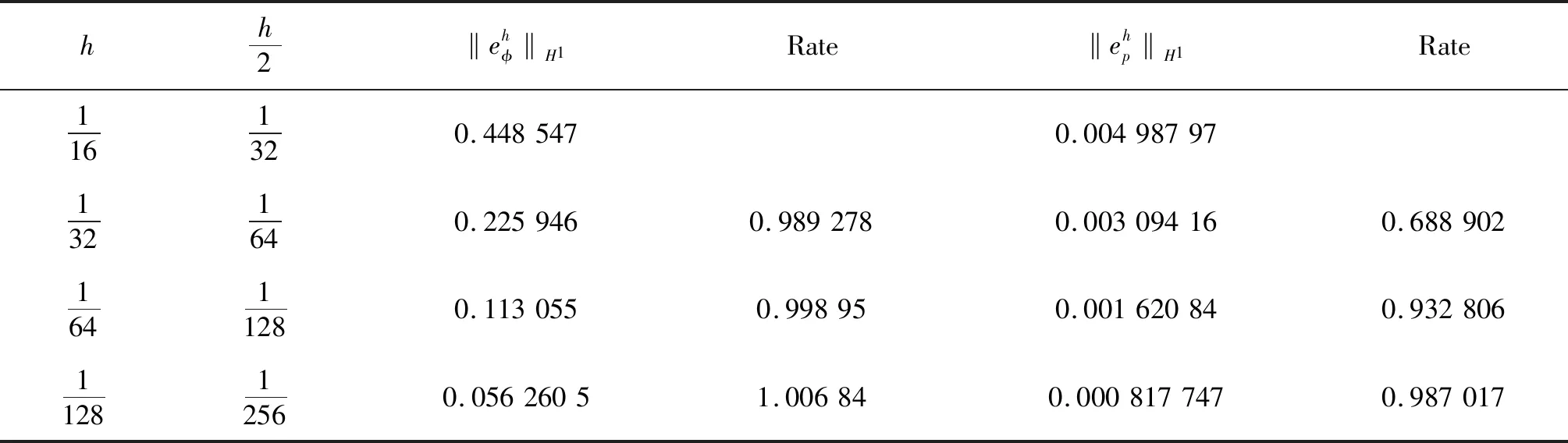
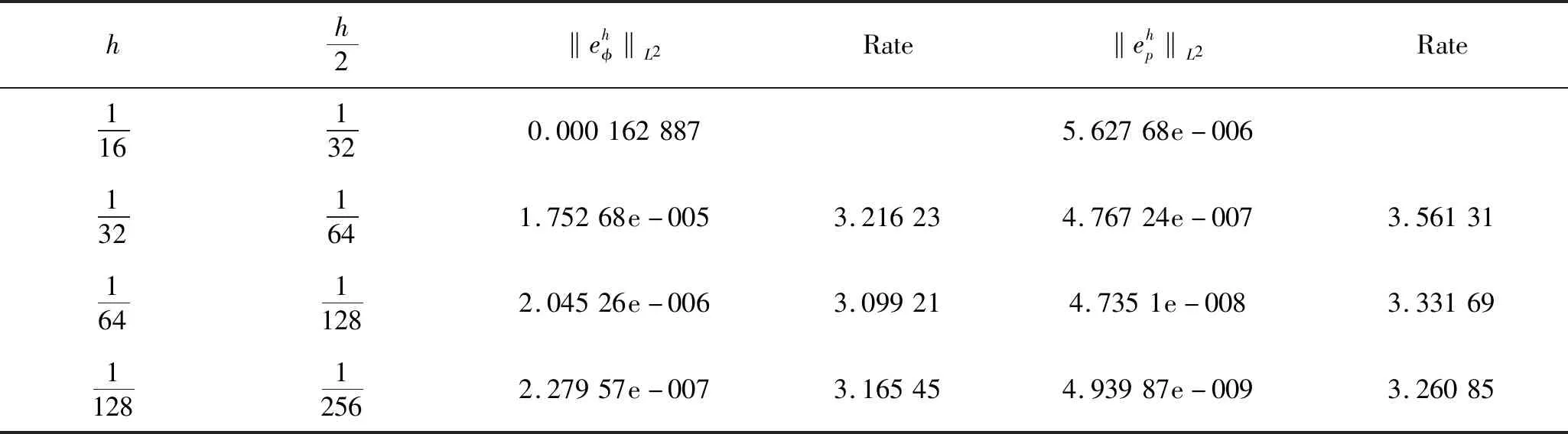
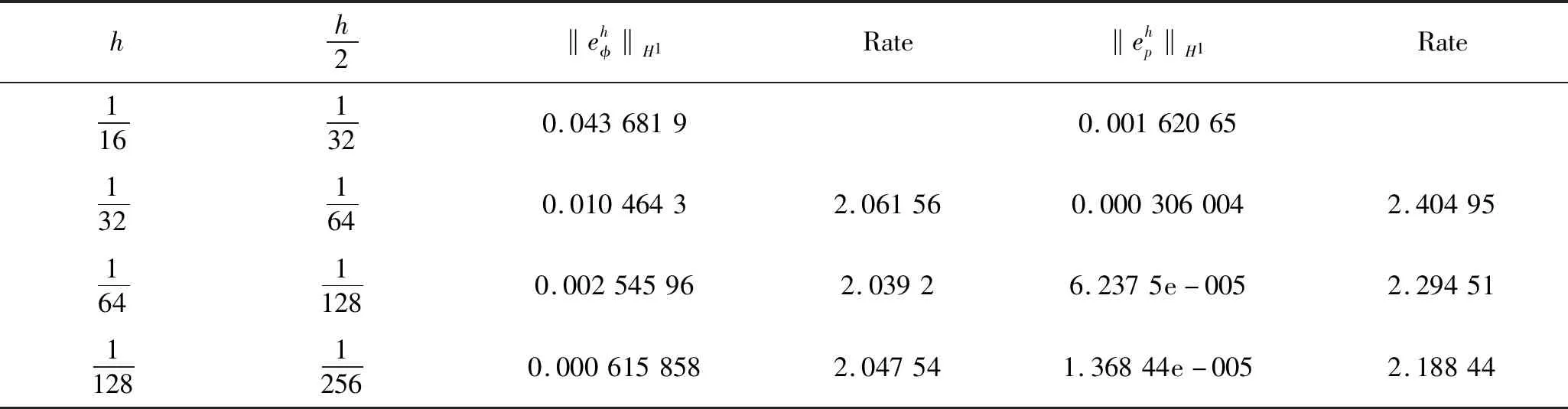
式中:Pe表示扩散的Peclet数;Ω⊂R2为开多边形或多面体区域;∂Ω为满足Lipschitz条件的边界;n是∂Ω上的外法向量;φ代表浓度;u代表速度;p表示压强;γ和ε都是正数;m(φ)表示流动系数,满足假设:0 含对数势的自由能密度函数[12]定义如下: (2) 式中θ<1。 (3) 式中κ∈(0,1)。其导数为: (4) (5) 可以发现CH-HS系统(1)是能量耗散的: (6) 并且是质量守恒的,即(φ(·,t),1)=(φ0,1),其中(·,·)表示在Ω上标准的L2内积。 CH-HS系统的变分形式为如下: (7) 这里f(φ)=f1(φ)-f2(φ),f2(φ):=φ,且: (8) 令0=t0 (9) 式中: un+1=-(μn+1) (10) (11) 对于任意的正整数r,定义Mh={vh∈C(Ω):|vh|K∈Pr, ∀K∈Th}⊂H1(Ω),这里Pr为阶数不超过r的多项式空间。 (12) (13) 证明:由定义 (14) 全离散格式(12)可以重写为: (15) (16) (17) (18) (19) 结合式(18)~(19)得: (20) (21) (22) (23) (24) 将式(22)~(24)结合,得: (25) (26) 利用Cauchy-Schwarz不等式,可知: (27) (28) 证毕。 在区域[0,1]×[0,1]上考虑CH-HS问题,初值取为: φ0=0.24·cos(2πx)cos(2πy)+ 0.4·cos(πx)cos(3πy) (29) 边界条件为: ∂nφ=∂nμ=0,u·n=0 (30) 令依赖于浓度的变系数函数为: (31) 其余参数分别为:Pe=20,θ=0.5,ε=0.05,γ=0.005,κ=0.01,τ=0.000 1,T=0.2。 表1~4呈现了对于所提格式利用不同的有限元计算的数值结果。 从表1~2可知,利用P1有限元计算,φ,p分别在L2范数下可以达到二阶精度,在H1范数下可以达到一阶精度。 从表3~4可知,利用P2有限元计算,φ,p分别在L2范数下可以达到三阶精度,在H1范数下可以达到二阶精度。 表1 利用P1有限元计算的L2范数下的数值结果Tab.1 Numerical results inL2norm by using P1 finite element 表2 利用P1有限元计算的H1范数下的数值结果Tab.2 Numerical results in H1norm by using P1 finite element 表3 利用P2有限元计算的L2范数下的数值结果Tab.3 Numerical results inL2norm by using P2 finite element 表4 利用P2有限元计算的H1范数下的数值结果Tab.4 Numerical results in H1norm by using P2 finite element 定义CH-HS的离散能量为: (32) 修正后的能量为: (33) 取参数τ=0.001,T=1,其余参数与表1中的相同。 图1表示了能量的稳定性质。 图1 能量变化图Fig.1 Evolution of energy 1) 区别于传统的多项式势的研究,研究对数势,对于对数势的处理,采用与含对数势的Cahn-Hilliard方程类似的正则化方法,并给出了相应的稳定性分析。 2) 分别利用P1有限元和P2有限元,进行数值模拟,得到了相应的精度。在未来的研究中,可以结合多重网格方法进行处理,进一步节省计算时间。
1.2 正则化问题


2 离散格式
2.1 半离散格式




2.1 全离散格式


3 稳定性分析



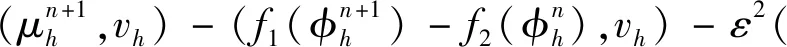
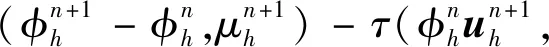

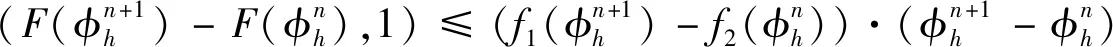

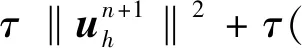

4 数值算例


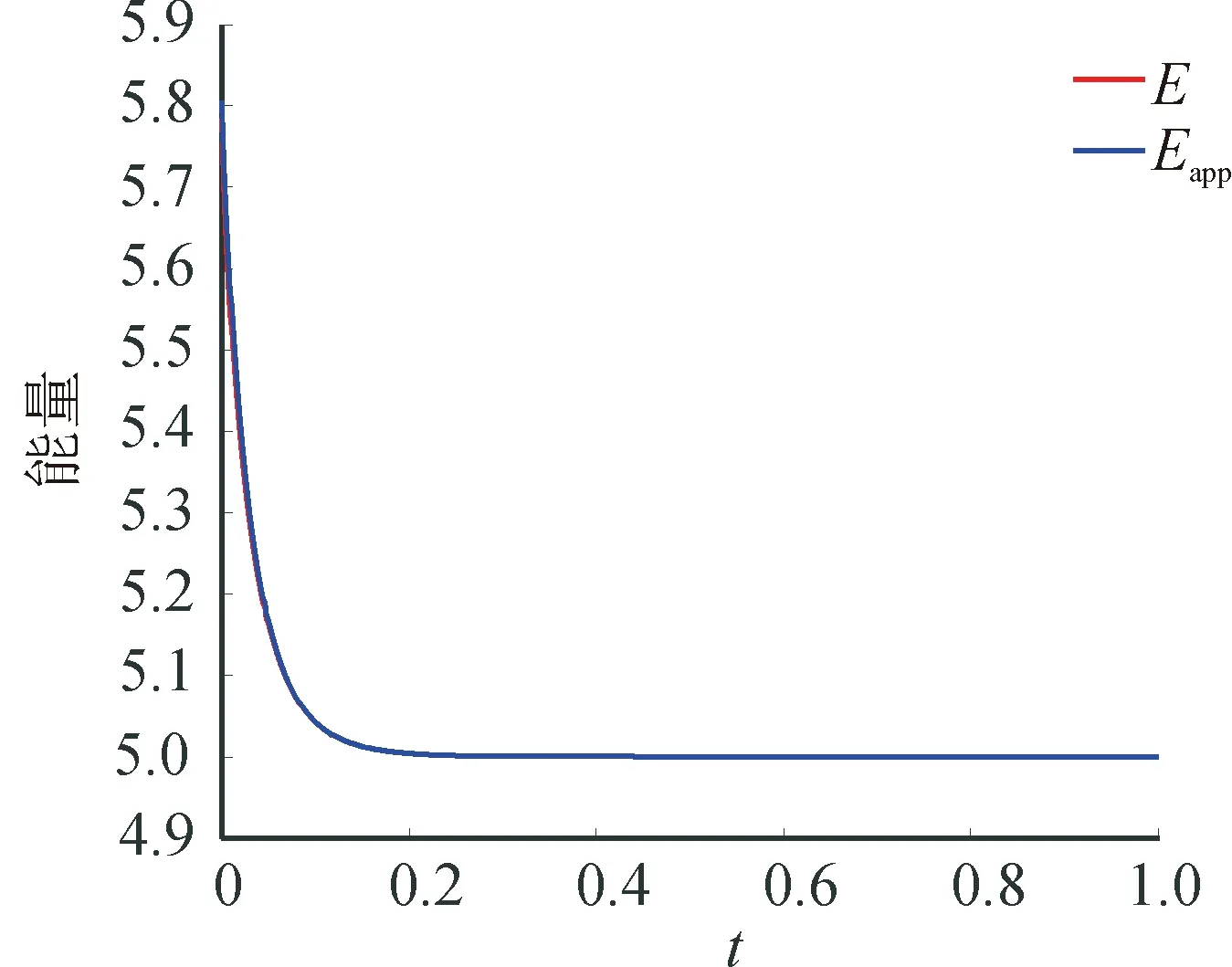
5 结 论
