城市轨道交通特定安全防护距离下的极限进站方案研究*
2019-03-15孔令发
孔令发
(上海富欣智能交通控制有限公司, 201203, 上海//工程师)
在城市轨道交通信号领域,为了保证列车能够安全进站,在线路终端站台后方需预留一定的安全防护距离。线路终端的安全防护距离由土建建设的客观条件决定,同时应兼顾建设成本来进行确定。因此,在特定(较短)的安全防护距离下,研究如何保证列车安全且高效进站具有十分重要的意义。
目前,我国通用的进站技术方案采用常用制动率进站方案。即在接近站台区域时,通过一个固定的常用制动率控制列车进站停靠站台。该方案无论对于车载ATO(列车自动运行)控车还是人工驾驶均有易控、易操作的优点,但同时存在以下问题:①为了保证进站效率,所需的站后安全防护距离较长;②在特定的安全防护距离下,只能通过降低进站效率来达到安全进站的目的。因此,研究一个兼顾行车安全、运营效率及建设成本的进站方案就显得颇为重要。
1 安全防护距离计算模型
安全防护距离是指在IEEE 1474.1标准中规定的列车安全制动模型中紧急制动曲线对应的目标停车点与常用制动曲线对应的目标点停车点之间的距离。其本质是附加在常用制动距离之上的安全富裕量,是CBTC(基于通信的列车控制)系统制动模型中的关键。它能保证列车在最不利的情况下发生紧急制动,也可停靠在安全停车点之前。安全防护距离模型如图1所示。
由以上模型,可以得到Sd的计算方法如下:
Sd=max(Sdi)
(1)
Sdi=deb(vi)-dsb(vi)
(2)
式中:
deb(vi)——在列车允许速度为vi处触发紧急制动,经过安全制动模型三阶段制动计算得出的紧急制动距离;
dsb(vi)——在列车允许速度为vi处触发常用制动,经过常用制动率制动停车的常用制动距离。
通过以上计算模型可以看出:为了减小安全防护距离,可以通过减小常用制动率,使常用制动距离增大,这样紧急制动距离与常用制动距离的差值减小,从而达到减小安全防护距离的目的。
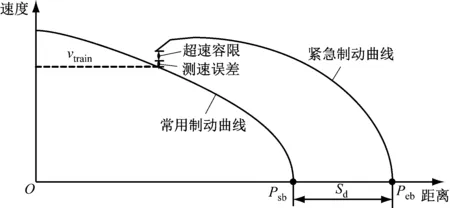
注:Sd表示安全防护距离; Peb表示紧急制动曲线上的目标停车点,即安全停车点;Psb表示常用制动曲线上的目标停车点,即运营停车点;vtrain表示列车运行速度
2 线路终端站台进站策略分析
当线路的终端位置及终端站台位置固定时,列车的进站示意如图2所示。
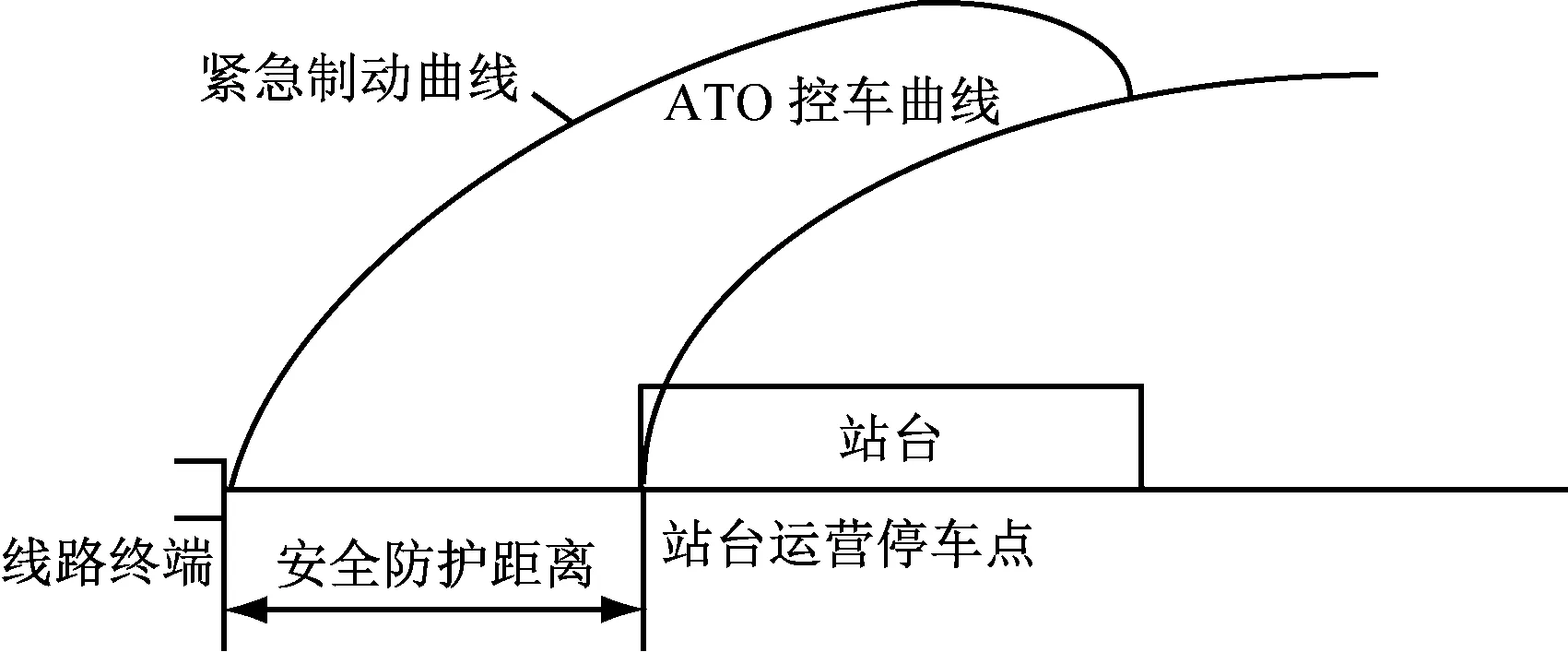
图2 线路终端位置及终端站台位置固定情况下的列车进站示意图
2.1 常用制动率进站分析
当线路终端和终端站台位置确定时,线路的安全防护距离长度一定,此时为了满足站台精确停车的运营需求,需要计算常用制动率。由上述分析可知,当安全防护距离较短时,只能通过减小常用制动率来满足列车能在站台停车点停车。然而,常用制动率的降低可带来进站速度降低、进站时间过长及乘客体验变差等诸多问题。
2.2 变制动率进站分析
当列车采用变制动率进站时,列车停站模型如图3所示。车载ATO控制列车沿着ATO允许速度曲线行驶,考虑在ATO允许速度的基础上叠加速度不确定性和超速容限后触发紧急制动,在安全制动模型规定的三阶段制动停车后,列车可安全地停靠在线路终端。
考虑极限情况,若要求运营停车点尽量靠近车档时,兼顾停站效率及舒适度,设计进站方案需考虑以下几个方面:
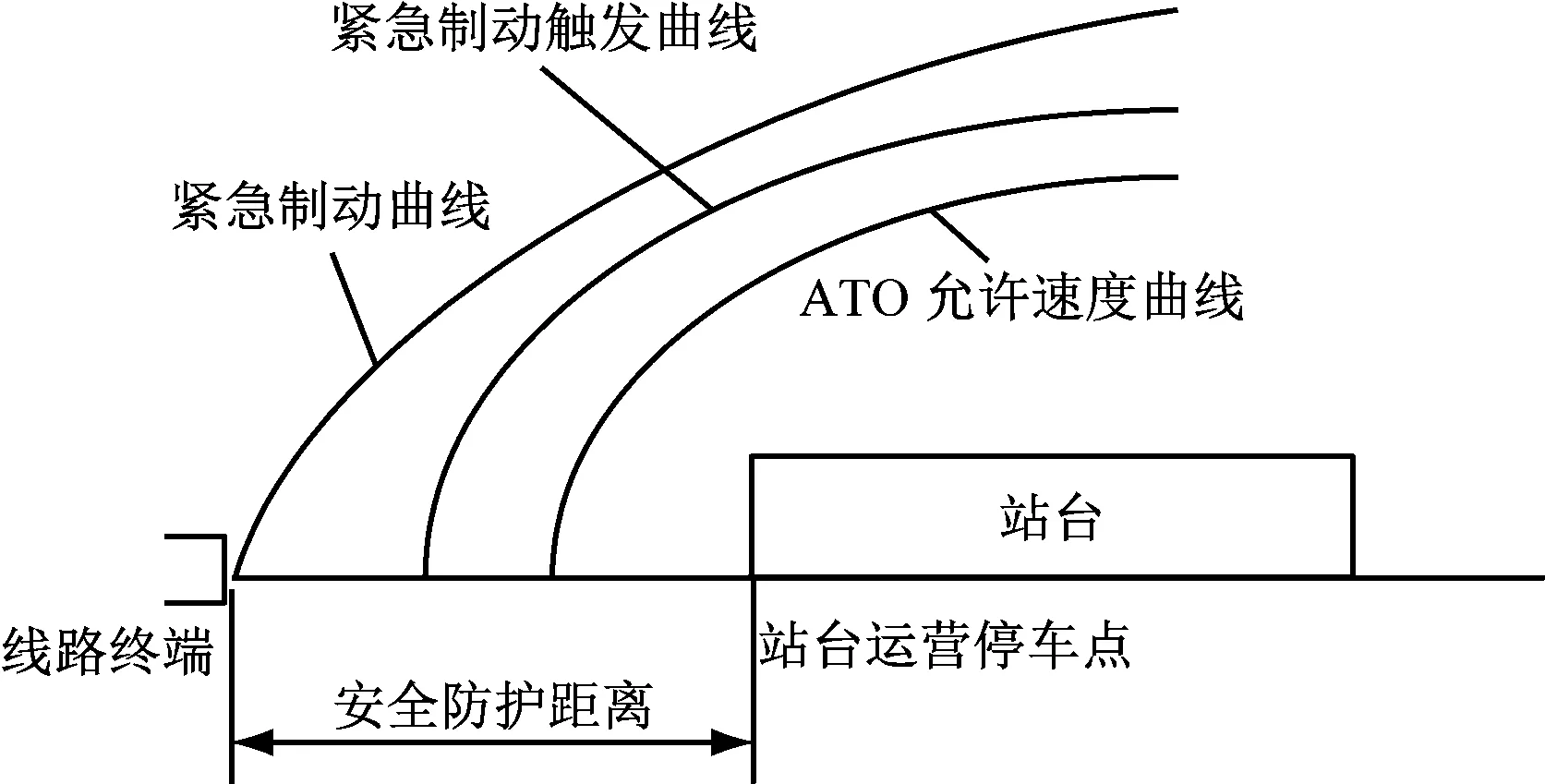
图3 列车采用变制动率进站示意图
(1) 计算并绘制紧急制动触发曲线。该曲线为安全曲线,当车辆特性参数发生变化时,会影响最终的停站距离(计算中已考虑了位置的不确定性)。
(2) 考虑站台区域速度不确定性和ATO控制范围,在紧急制动触发曲线的基础上,减去超速容限,得到允许速度-距离曲线。该曲线为ATO可控制行车曲线。
(3) 当列车进站靠近终端时,列车速度和加速度均已很小,车辆特性决定此时通过ATO控制已很难调整,此时ATO保持当前加速度进站并对准站台进行停靠。
(4) 列车停站过程中,需考虑乘客舒适性及冲击极限的要求。
3 上海某轨道交通线路变制动率进站方案仿真分析
3.1 仿真参数选取
为了验证列车采用变制动率进站策略的可行性,以及将其与常用制动率进站策略进行对比,选取上海某轨道交通线路的典型参数对该方案进行仿真分析。选取的参数如表1所示。
3.2 仿真结果分析
3.2.1 列车采用常用制动率进站方案
图4为安全防护距离与常用制动率关系图。由图4可知,当满足11.8 m的安全防护距离时,常用制动率为0.3 m/s2。
此时列车在站台边缘的进站速度为7.53 m/s,列车从到达站台边缘至完全停止所用的时间为25.09 s。
3.2.2 列车采用变制动率的极限进站方案
图5为采用变制动率的极限进站方案时列车运行速度与安全防护距离关系图。由图5可知,当ATO控制列车完全按照ATO允许速度曲线行驶时,经仿真可得列车最近可停靠在距离安全停车点8.01 m的位置。但实践表明,当ATO允许速度较低时,由于车辆特性的影响,会导致ATO控车精度变差。
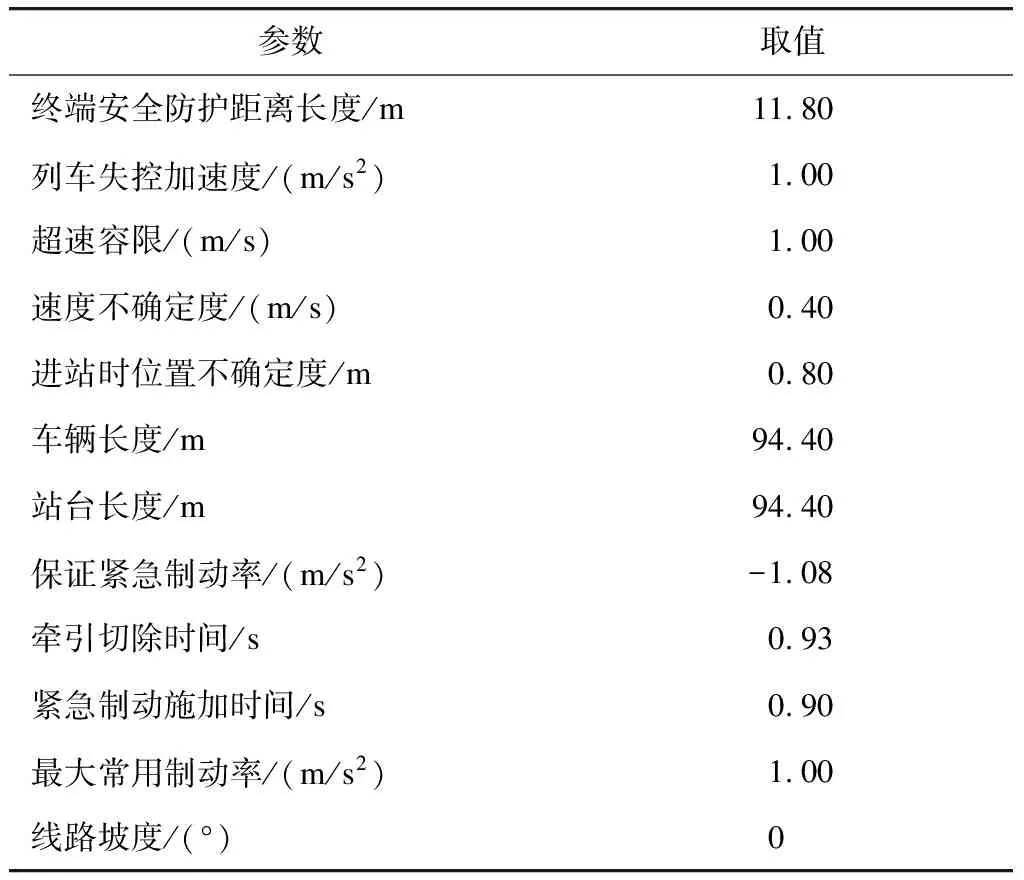
表1 上海某轨道交通线路变制动率进站方案参数表
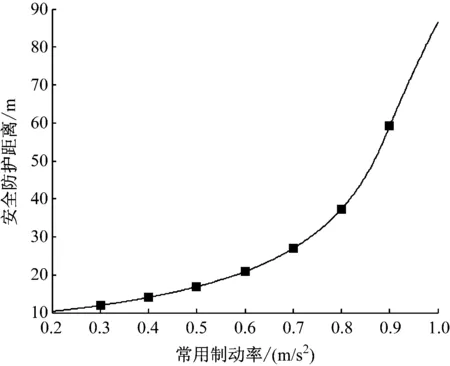
图4 安全防护距离与常用制动率关系图
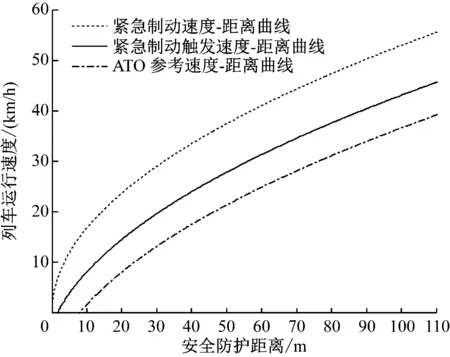
图5 列车运行速度与安全防护距离关系图
通过仿真可得ATO允许速度-距离曲线上对应的加速度(见图6)。由图6可知,当列车靠近停车点时, ATO控车的加速度也逐渐减小,此时 ATO采用变制动率控车的难度变大,相应精度变差。因此,采用优化的控车策略,即列车在接近停车点时采用固定制动率进行对准停车。
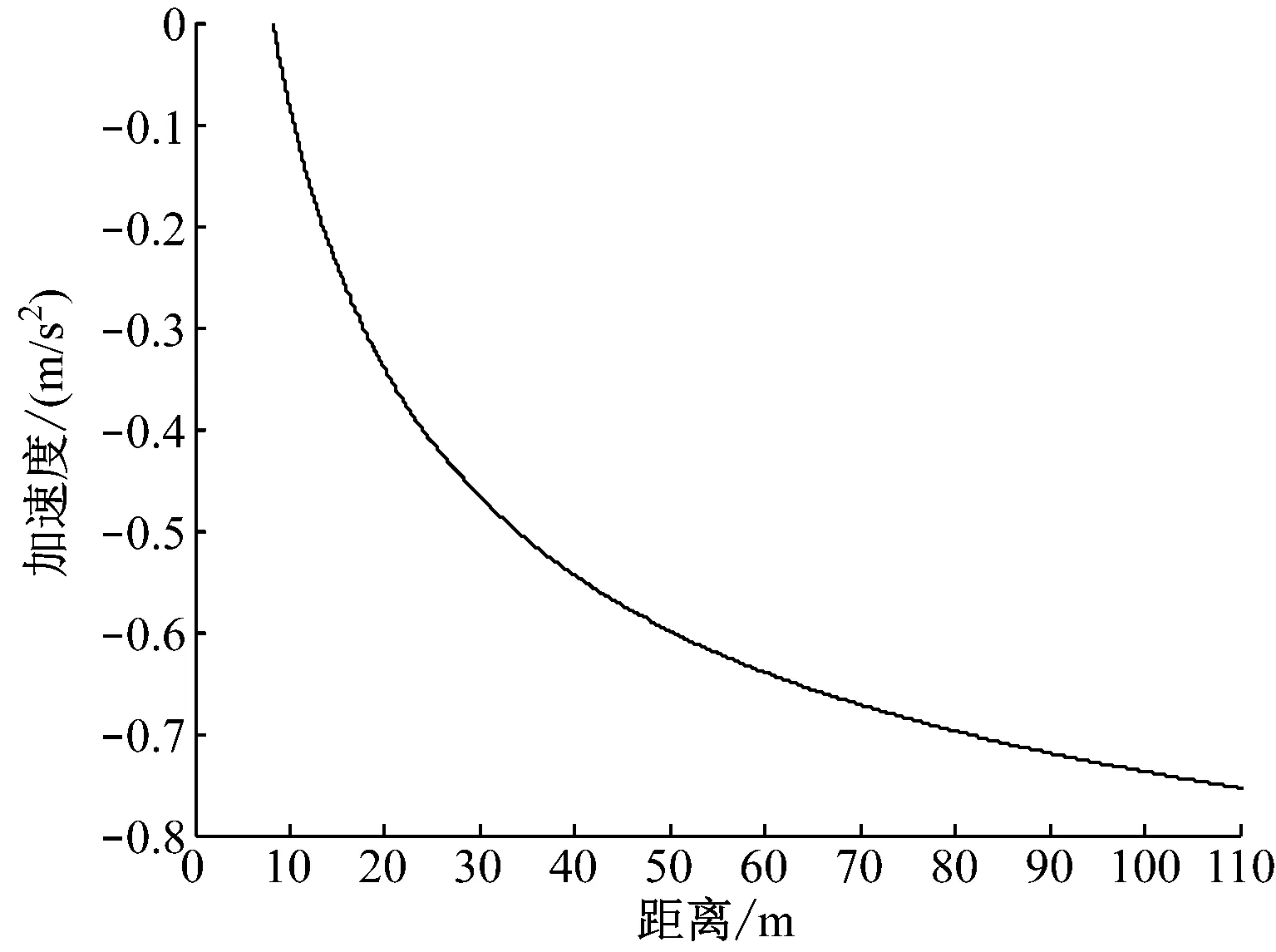
图6 ATO控车加速度-距离曲线
为了让列车准确地停靠在站台停车点处,即满足安全防护距离为11.8 m的要求,此时可以在ATO允许速度-距离曲线上选取一个点,ATO控制列车行驶至该点时,采用该点固定的制动率将列车停下。假设该点的速度为vs,加速度为as,则该点的选取需满足Ssbm与Sser的差值为11.8 m。其中,Ssbm表示在当前vs下,按照安全制动模型三阶段停车的制动距离;Sser表示在当前vs下,按照固定制动率停车的制动距离。
通过仿真可得“变制动率+固定制动率”下的速度-距离曲线,如图7所示。
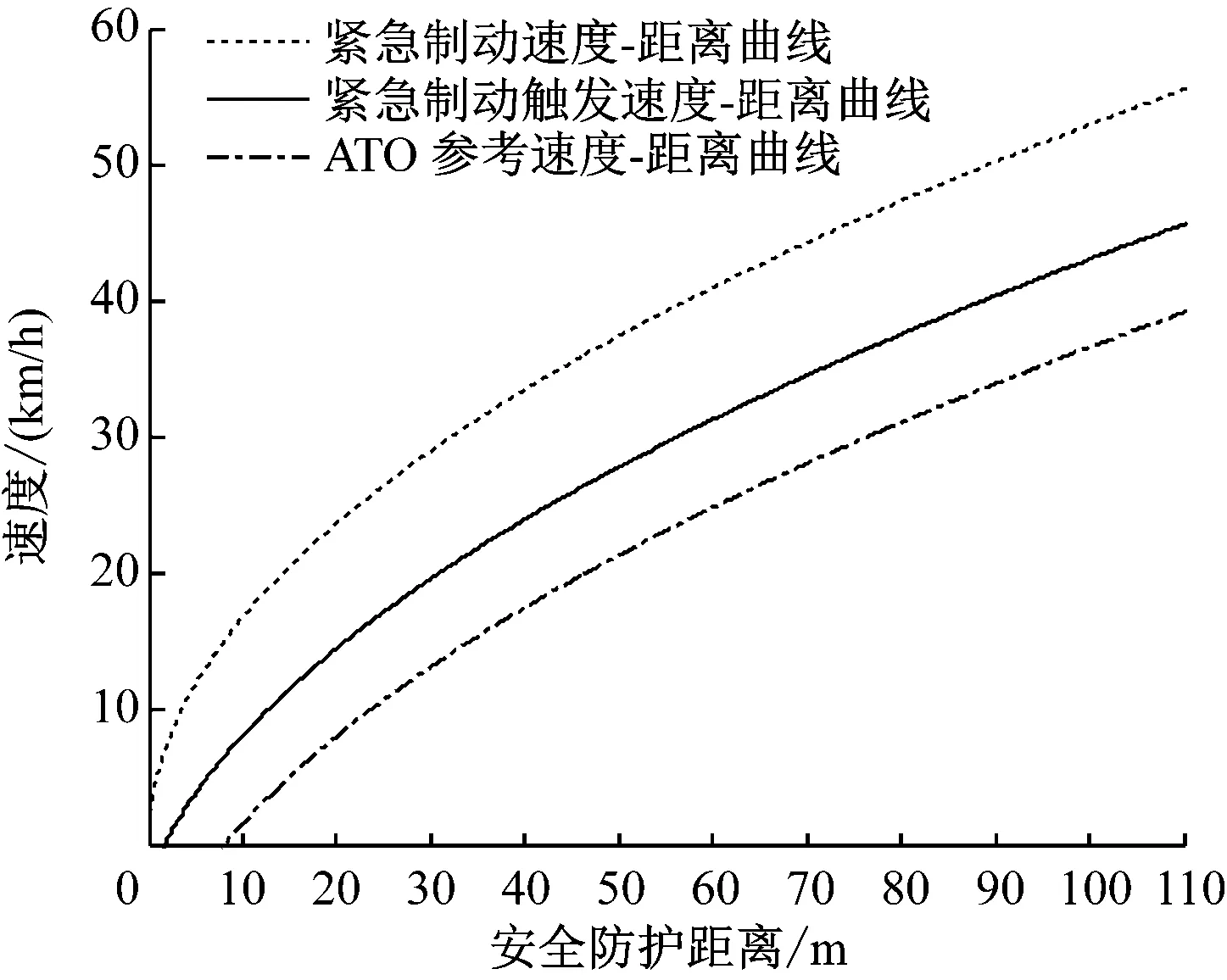
图7 “变制动率+固定制动率”下的速度-距离曲线
图7中,当列车距安全防护点的距离为17.16 m时,可按照此刻的固定加速度-0.3 m/s2将列车停下。此时计算得出列车在站台边缘处的速度为10.61 m/s,列车从站台边界至完全停车所用的时间为20.9 s。
4 结论
(1) 当列车采用变制动率进站的方案时,在极限情况下,可缩短站后的安全防护距离,适应土建建设的客观条件,降低土建建设成本。
(2) 采用变制动率进站的方案,在终端安全防护距离一定时,可提高进站效率,同时在考虑效率、旅客舒适度的平衡时,可在速度较低时选用更为平滑的固定制动率进站,此时速度曲线更为平滑,提高了旅客舒适度。
