基于降低悬挂式单轨车辆侧滚的结构参数优化研究*
2019-03-15杜子学
唐 飞 杜子学
(1.重庆中车长客轨道车辆有限公司,401133,重庆;2.重庆交通大学轨道交通研究院,400074,重庆//第一作者,教授)
悬挂式单轨作为一种轻型、中速、中运量的新型公共交通方式,具有施工简单、费用低、工期短、受地面交通干扰小、爬坡能力和曲线通过能力强、噪声低和乘坐舒适等特点[1]。其可与常规道路公交、轨道交通等其它公交方式错位发展、互为补充,是其他公共交通方式的有益补充和完善。
由于悬挂式单轨车辆结构和运行方式的独特性,在曲线入口、出口处的缓和曲线区间,车辆受曲线离心力作用发生较大侧滚[2],乘客需要频繁控制身体不发生倾斜,容易引起乘客身体疲倦,影响车辆运行稳定性和舒适性。因此,有必要对悬挂式单轨车辆在曲线运行时产生的较大的侧滚开展研究。
1 悬挂式单轨车辆模型的建立
1.1 悬挂式单轨结构
悬挂式单轨交通系统的车体是悬挂在轨道梁的下方,车辆转向架、走行轨面、导向轨面及电力通信系统均安装在下部有开口的轨道梁内部,走行轮和导向轮沿着轨道梁内部铺设的走行轨面和导向轨面行驶[3]。轨道梁由支柱支承,支柱可采用混凝土结构或钢管结构。悬挂式单轨交通系统的结构如图1所示。
1.2 转向架结构
悬挂式单轨车辆转向架是其最独特的组成部分。悬挂式单轨车辆转向架主要由构架、走行轮、导向轮、空气弹簧、枕梁、横向拉杆、中心销、吊架、安全钢索、横向减振器、牵引电机和差速装置等组成。悬挂式单轨车辆转向架结构如图2所示。
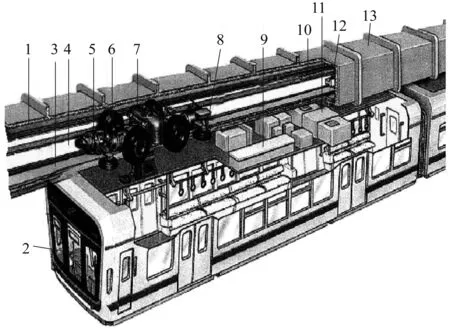
注:1——正极导电轨;2——列车自动控制;3——走行路面;4——导向轨;5——牵引电机;6——走行轮;7——摇枕装置;8——导向轮;9——主控制器;10——信号系统;11——空调装置;12——负极导电轨;13——轨道梁
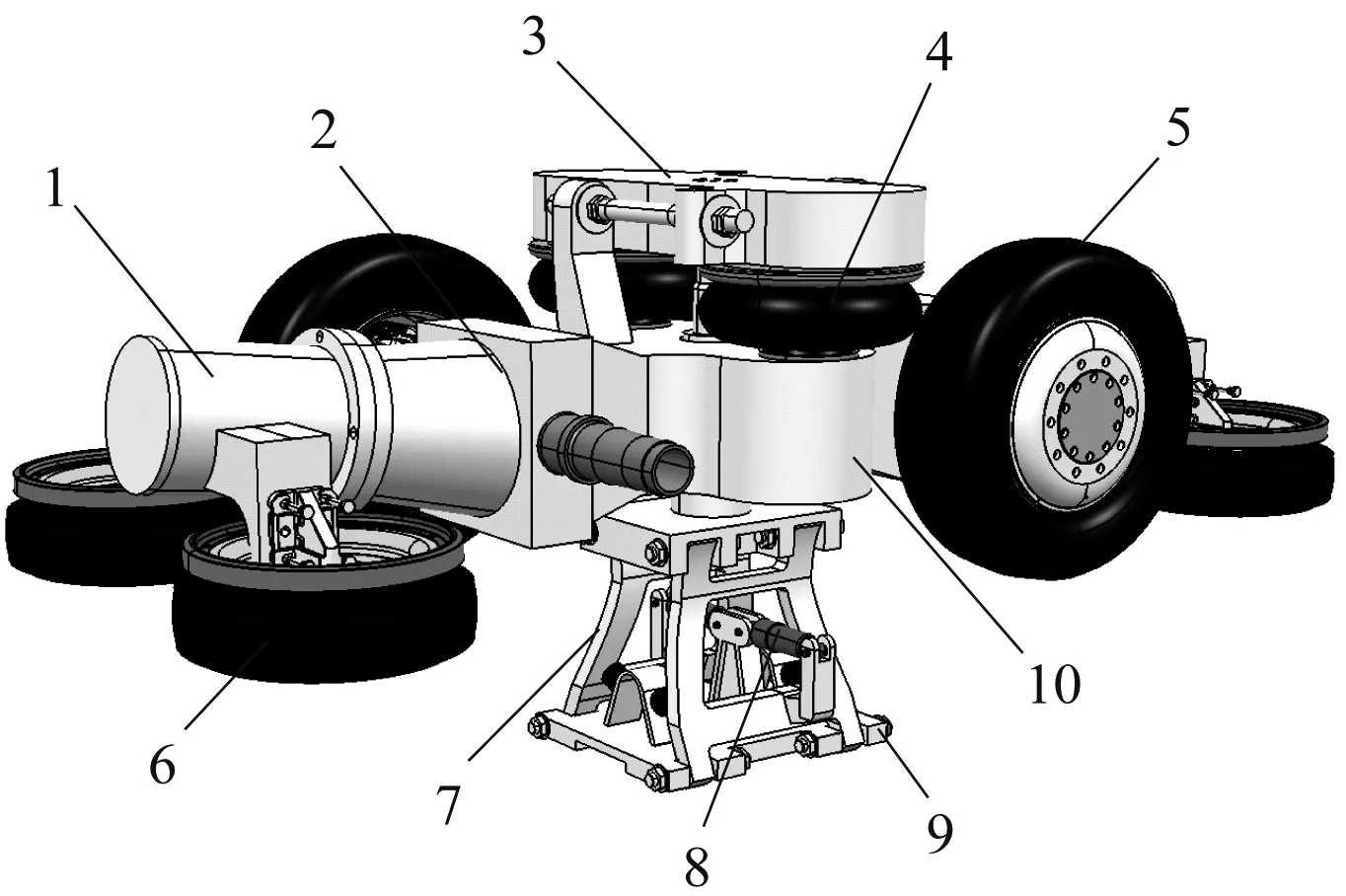
注:1——牵引电机;2——齿轮箱;3——枕梁;4——空气弹簧;5——走行轮;6——导向轮;7——悬吊装置;8——减振器;9——车体连接座;10——构架
1.3 车辆拓扑构型
通过分析悬挂式单轨车辆结构,得到悬挂式单轨车辆动力学关系拓扑构型,如图3所示。
2 悬挂式单轨车辆动力学模型的建立
按照悬挂式单轨车辆动力学关系拓扑构型,运用多体动力学软件ADAMS建立悬挂式单轨车辆动力学模型,如图4所示。采用国标GB 7031—1986《车辆振动输入-路面平度表示方法》中的A级路面来模拟轨道不平顺[5]。线路参数如表1所示。
3 悬挂式单轨车辆结构参数的敏感性分析
由于悬挂式单轨车辆结构和运行方式的独特性,在离心力的作用下,车辆通过曲线时产生的侧滚较大。悬挂式单轨车辆通过曲线时车体的侧滚状态如图5所示。针对悬挂式单轨车辆通过曲线时的侧滚状态,从机构优化的角度,以走行轮、导向轮、中心销、吊架、吊架底座、横向减振器、横向止挡、横向拉杆的空间位置为设计变量,研究影响车辆侧滚的主要结构参数,共设置23个优化变量。
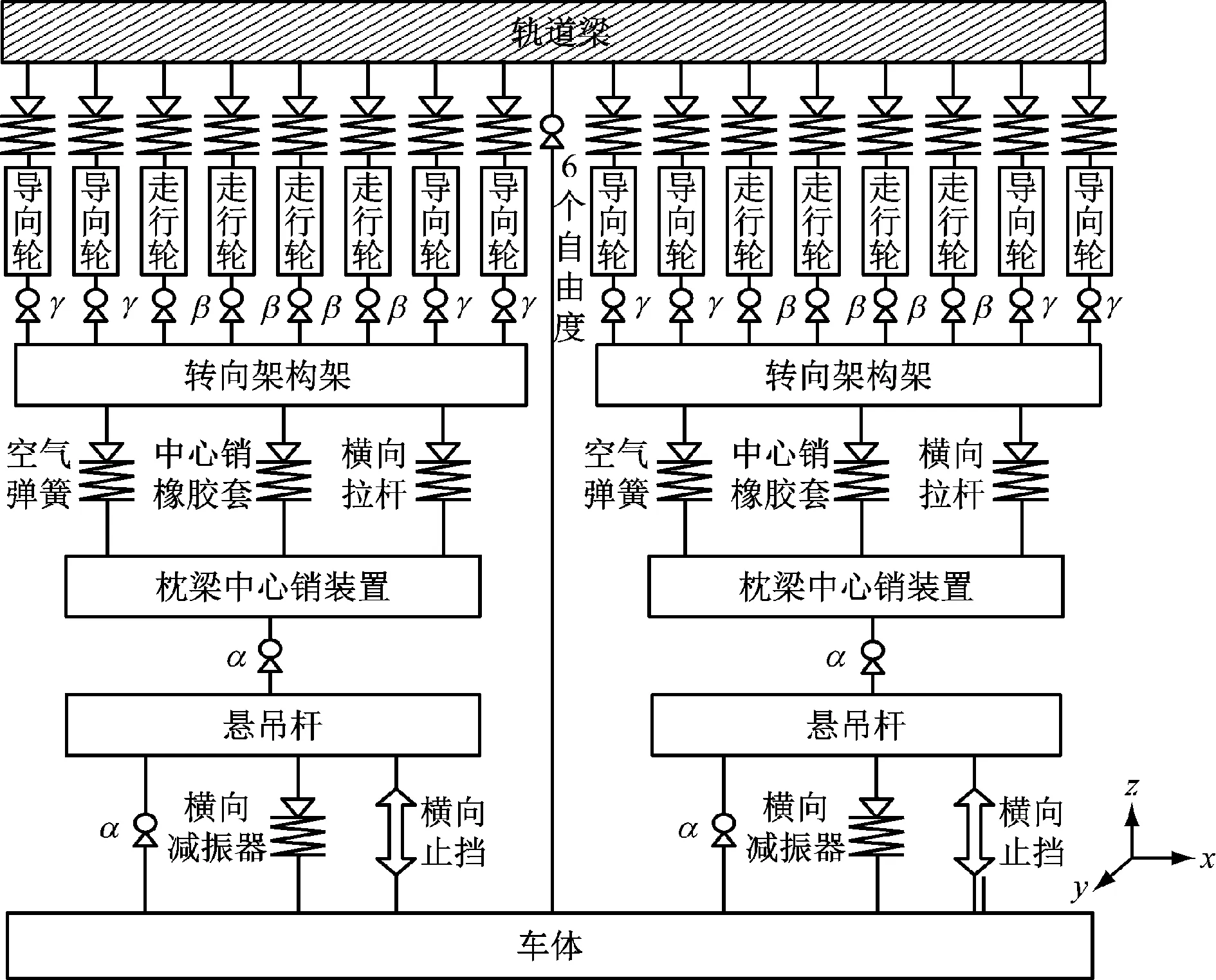
注:α,β,γ分别代表绕x、y、z轴的自由度
图4 悬挂式单轨车辆动力学模型
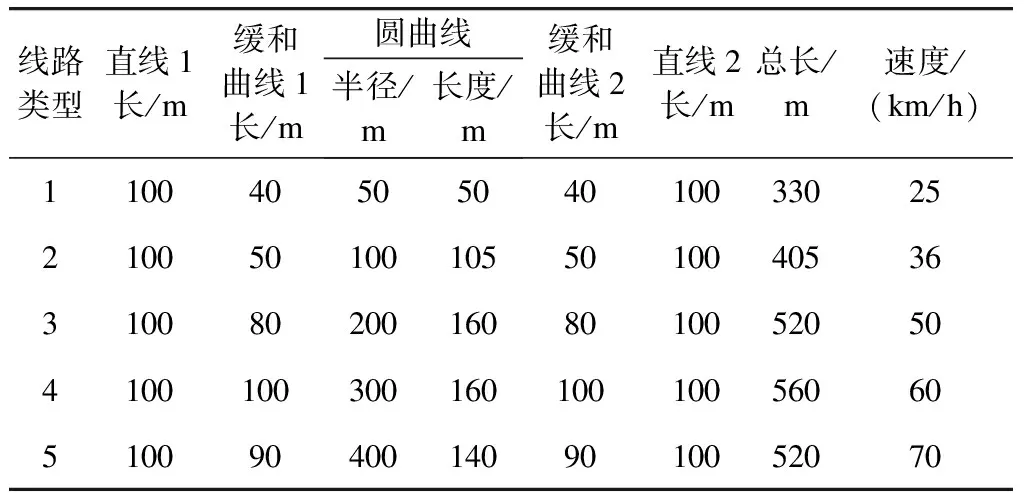
表1 线路参数表
Mode FRONTIER软件具有模型参数灵敏度分析的功能,可对动力学模型中的参数进行全局灵敏度分析。为研究结构参数对车辆侧滚的灵敏度影响,首先需设置23个结构参数的取值范围,如表2所示。

注:F表示车辆受到的离心力;G表示车辆受到的重力
利用Mode FRONTIER软件中的建模功能,建立悬挂式单轨车辆结构参数灵敏度分析模型,如图6所示。
悬挂式单轨车辆结构参数灵敏度分析模型建立之后,采用Mode FRONTIER软件中的标准化回归系数法对影响因子进行定性和定量的全局灵敏度分析。各结构参数定性灵敏度分析的可视化柱状图如图7所示。

表2 敏感性试验参数表
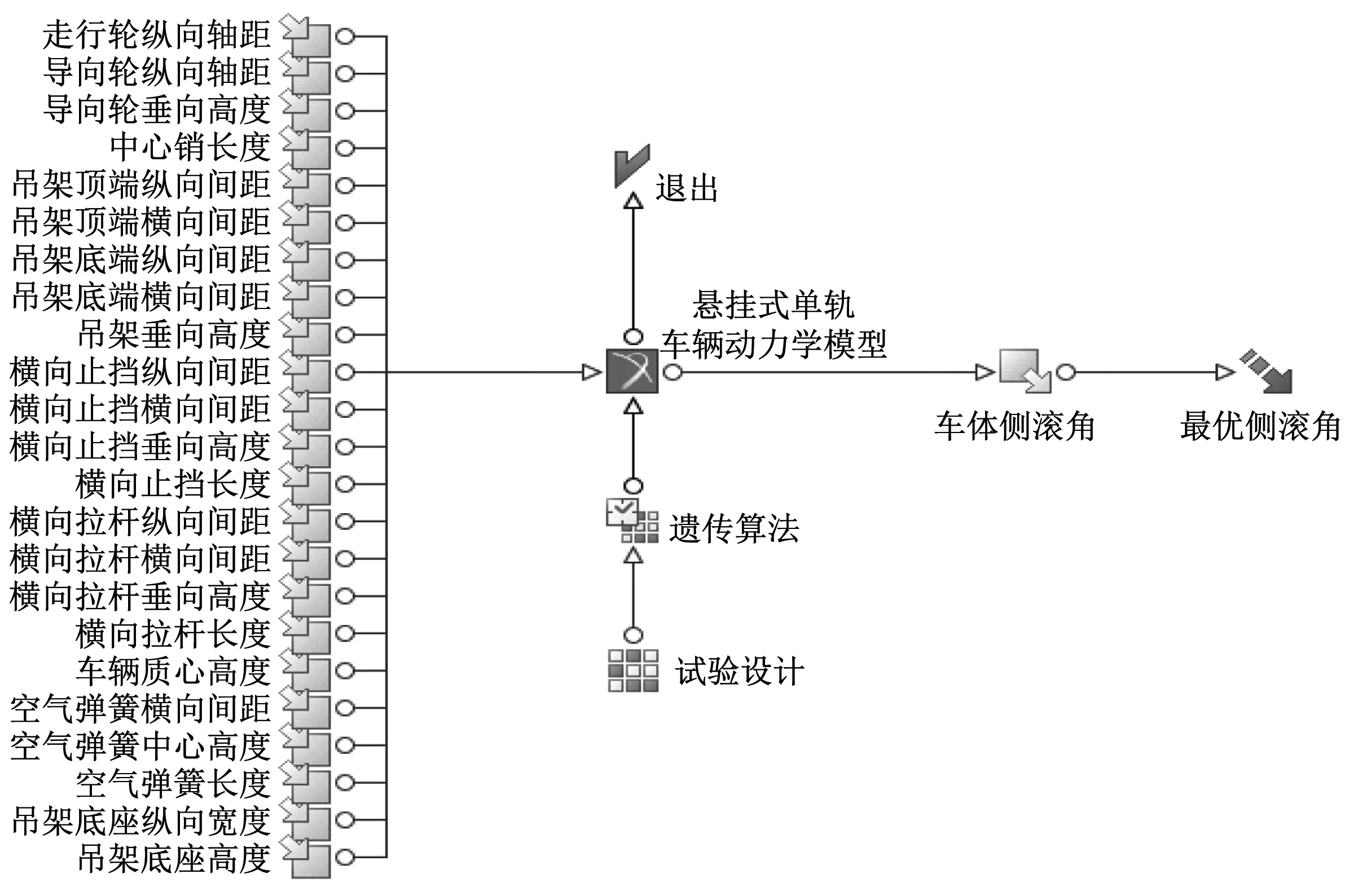
图6 悬挂式单轨车辆结构参数敏感度分析模型
通过对灵敏度计算结果进行分析,得到主要影响悬挂式单轨车辆结构侧滚的9个结构参数为空气弹簧中心高度、导向轮垂向高度、横向拉杆纵向间距、吊架底端横向间距、空气弹簧横向间距、吊架底端纵向间距、横向止挡高度、横向拉杆长度和横向止挡纵向间距。其中,空气弹簧中心高度、横向止挡纵向间距对侧滚的影响为正相关;导向轮垂向高度、横向拉杆纵向间距、吊架底端横向间距、空气弹簧横向间距、吊架底端纵向间距、横向止挡高度、横向拉杆长度对侧滚的影响为负相关。本文将选取以上9个主要参数对悬挂式单轨车辆的侧滚进行优化。

图7 悬挂式单轨车辆结构灵敏度分析柱状图
4 悬挂式单轨车辆侧滚模型优化
4.1 优化变量及目标的确立
根据灵敏度分析,选取空气弹簧中心高度、导向轮垂向高度、横向拉杆纵向间距、吊架底端横向间距、空气弹簧横向间距、吊架底端纵向间距、横向止挡高度、横向拉杆长度和横向止挡纵向间距为主要优化变量,并以车辆侧滚为优化目标函数。
4.2 约束条件的确立
车辆通过曲线时应具有良好的通过性与稳定性,由于悬挂式单轨车辆不存在倾覆与脱轨等现象,所以拟采用的约束条件为:轮重减载率应小于0.6,走行轮最大垂向力应小于43.39 kN,以及导向轮最大径向力应小于23.05 kN[6]。
4.3 优化模型的建立
运用Mode FRONTIER与 ADAMS建立联合优化模型,如图8所示。模型采用NSGA-II遗传算法,并进行多次迭代,最后9个结构参数及目标函数均收敛于一点,如图9所示。
通过优化得出空气弹簧中心高度为393.9 mm、导向轮垂向高度为122.8 mm、横向拉杆纵向间距为144.1 mm、吊架底端横向间距为272.5 mm、空气弹簧横向间距为181.8 mm、吊架底端纵向间距为459.1 mm、横向止挡高度为1 030.1 mm、横向拉杆长度为492.1 mm、横向止挡纵向间距为202 mm时车体侧滚角达到最优。为了对优化效果进行验证,本文选取半径分别为40 m、45 m、50 m和100 m时的4种典型弯道对优化效果进行验证,优化结果对比分析如表3和图10所示。由表3和图10可知,优化后车体侧滚角降低了6.3%~11.4%。
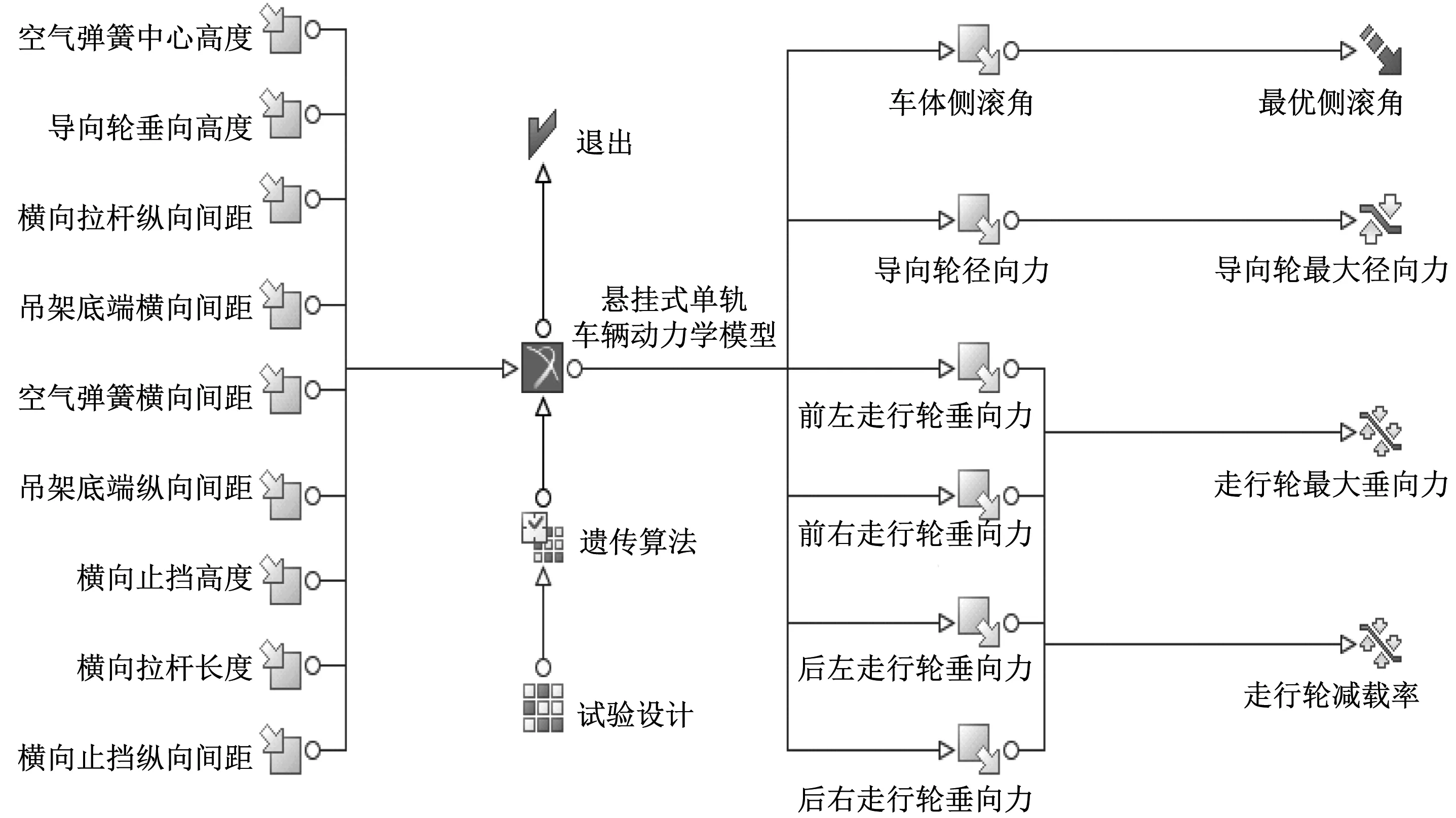
图8 Mode FRONTIER与ADAMS的联合优化模型
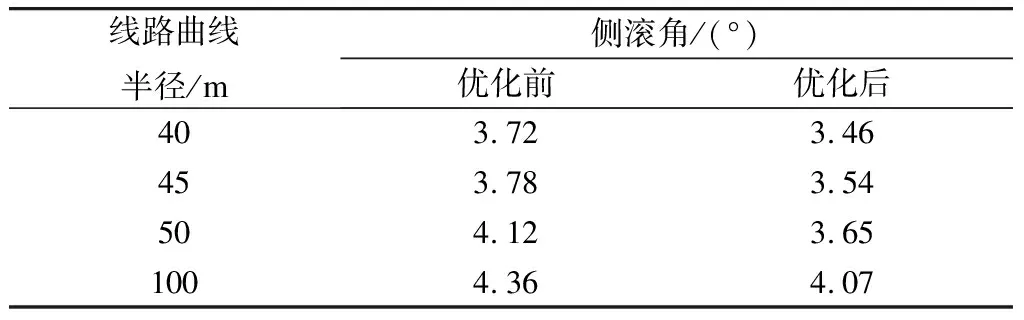
表3 车体侧滚角
5 结语
(1) 针对悬挂式单轨车辆侧滚较大问题,从机构优化的角度,开展了车体侧滚的影响因子分析。通过分析发现空气弹簧中心高度、导向轮垂向高度、横向拉杆纵向间距、吊架底端横向间距、空气弹簧横向间距、吊架底端纵向间距、横向止挡高度、横向拉杆长度和横向止挡纵向间距是影响悬挂式单轨车辆侧滚的主要结构参数。
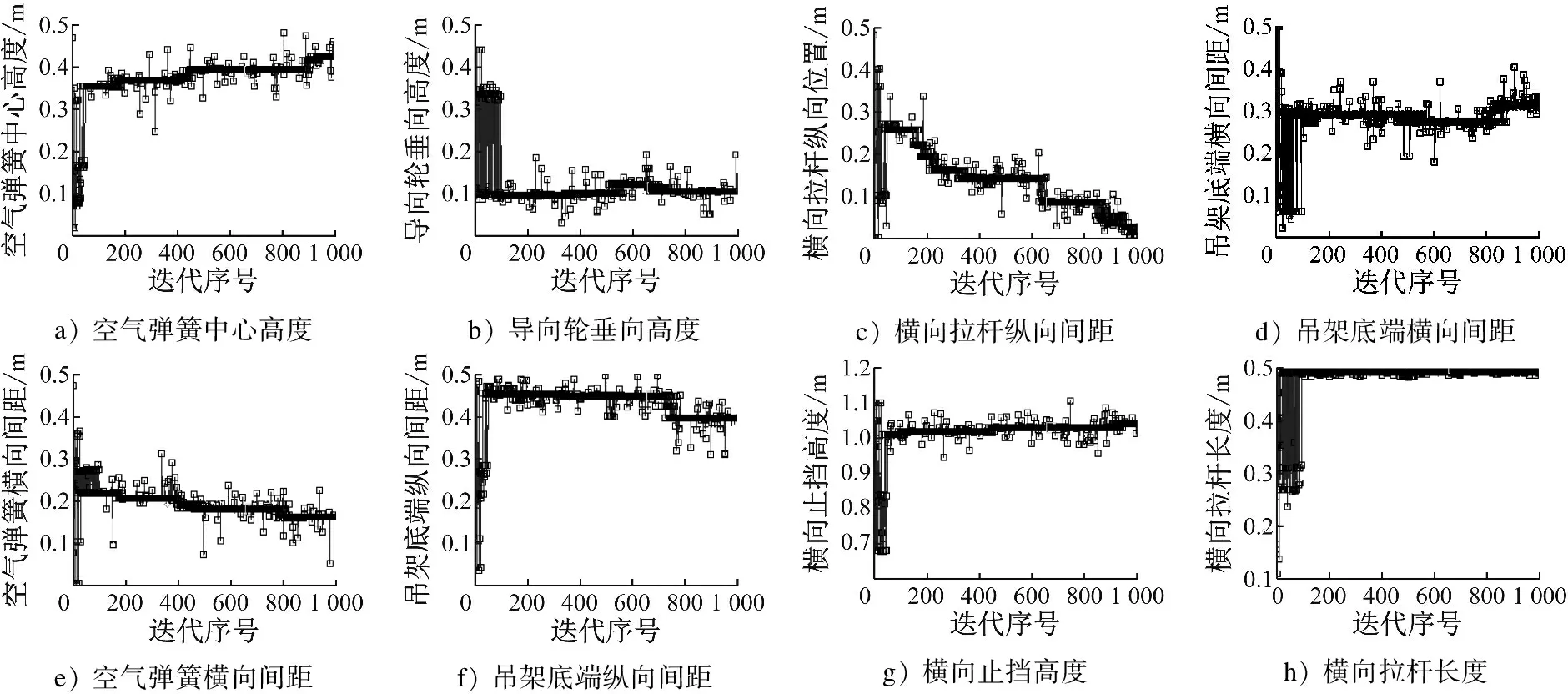
a) 空气弹簧中心高度b) 导向轮垂向高度c) 横向拉杆纵向间距d) 吊架底端横向间距e) 空气弹簧横向间距f) 吊架底端纵向间距g) 横向止挡高度h) 横向拉杆长度
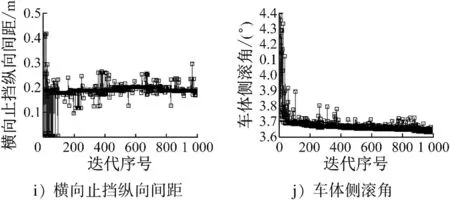
图9 优化模型中各参数及目标迭代过程
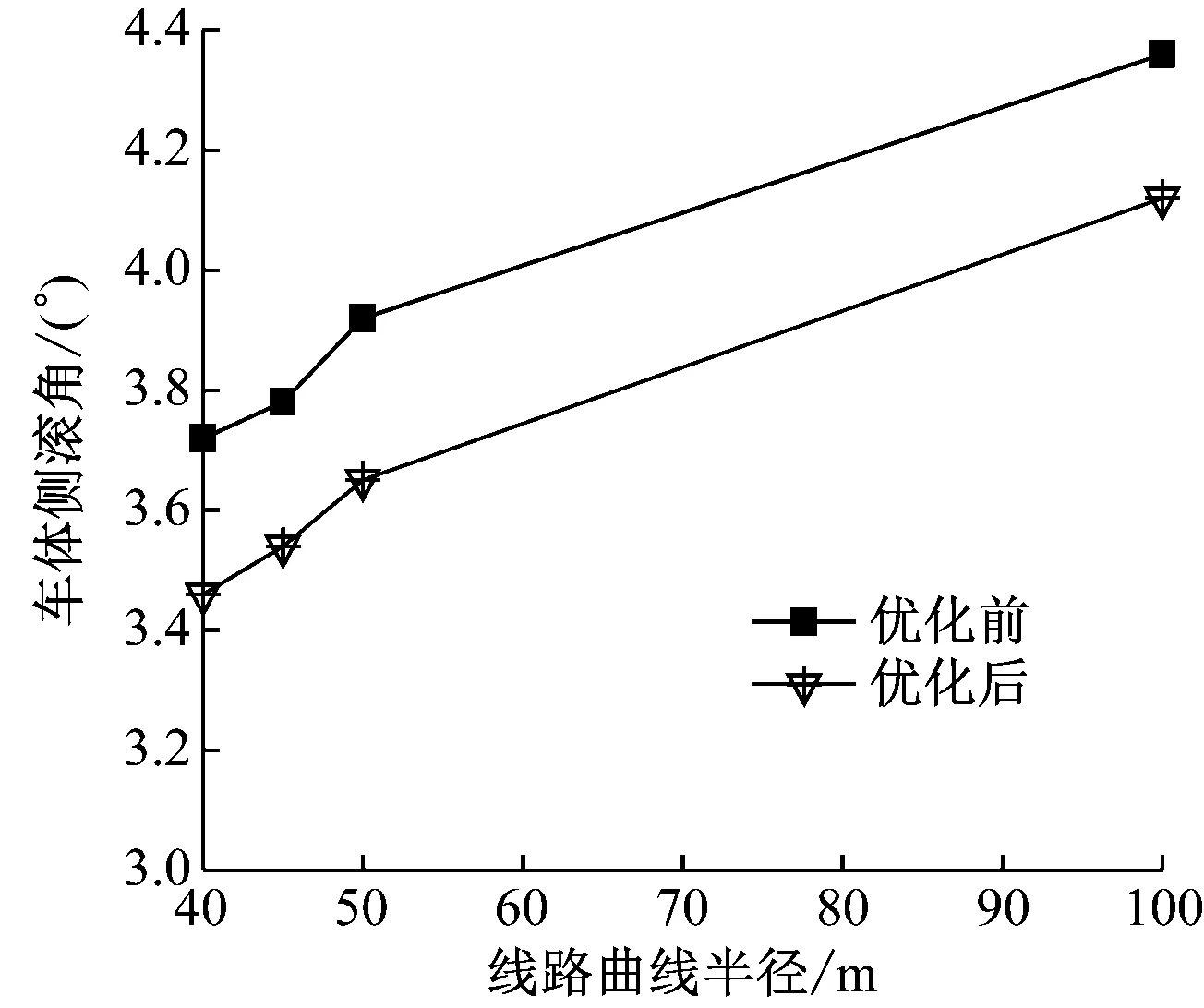
图10 模型优化前后车体侧滚角对比
(2) 当空气弹簧中心高度为393.9 mm、导向轮垂向高度122.8 mm、横向拉杆纵向间距144.1 mm、吊架底端横向间距272.5 mm、空气弹簧横向间距181.8 mm、吊架底端纵向间距459.1 mm、横向止挡高度1 030.1 mm、横向拉杆长度492.1 mm、横向止挡纵向间距202 mm时车体侧滚角达到最优,此时车体侧滚角由3.72°降低至3.46°,降低幅度为6.9%。
(3) 选择曲线半径分别为40 m、45 m、50 m、100 m时的4种典型线路类型对优化效果进行验证,结果显示,车体侧滚角降低了6.3%~11.4%,说明优化方案具有可行性和普遍性。
