重质船用燃料油黏度预测模型研究
2019-03-15刘名瑞王晓霖王海波
刘名瑞,王晓霖,王海波,于 阳,王 刚
(1.中国石化大连(抚顺)石油化工研究院,辽宁 大连 116045;2.中国石化燃料油销售有限公司辽宁分公司)
重质船用燃料油是用于大型中低速船用柴油机的燃料,也称为残渣型燃料油,通常是直馏渣油、减压渣油和一定比例的轻组分混合而成[1-2]。这种调合燃料油的产品性质主要取决于调合方案,因此,计算调合方案时对调合产品的指标预测就显得尤为重要。黏度作为重质船用燃料油的首要指标,若采用线性模型进行预测,误差较大,严重影响调合生产。因此,对重质船用燃料油黏度预测模型的研究与应用至关重要。
在原油指标预测方面可借鉴的经验式很多[3-5],但由于燃料油调合组分的性质差异而并不适用。常用的燃料油调合组分油有渣油、页岩油、煤柴、油浆等,这些组分油的黏度跨度很大,从几十mm2/s到几万mm2/s。其中,煤柴是指中、低温煤焦油通过分馏装置提炼而出的二次炼油产物。若调合方案中组分油之间的黏度差异较大,黏度大的组分所占比例每增加1%,调合产品的黏度就会上浮10%~20%,很容易造成产品超过国家标准要求而不合格。相反,若减少黏度大的组分油,又容易出现黏度过低而不适合船用发动机使用的情况。因此,对调合产品的各项指标进行精确预测,优化调合比例,可有效降低产品不合格风险,避免资源浪费,同时提高生产效率。有些性质指标如黏度、闪点、凝点等,其计算式属于非线性关系,计算过程较复杂,需选用特定的物理模型公式计算[6]。另外,除了通过一般物理模型进行预测外,还可以通过具有一定逻辑公式的计算模型进行预测,如蛛网模型、神经网络模型、最小二乘支持向量机模型等[7-9]。这类模型需要通过建模来实现,且具有更高的精确度[10],但是操作难度相对较大。
本课题主要研究现有黏度预测模型应用于重质船用燃料油黏度预测的可行性,筛选几种常见的黏度物理模型,进行试验数据对比和最优模型选取,基于重质船用燃料油数据库对Cragoe模型进行修正,并结合掺稀降黏试验数据分析混合机制对预测模型相对误差的影响。
1 常用黏度预测模型
黏度是重质船用燃料油中最为重要的性质指标,是划分油品牌号的依据,因此,对适用于重质船用燃料油的黏度模型进行研究,有利于指导调合生产。现有的物理预测模型常用于原油调合,对具有高黏度比的混合原油的黏度预测大多是基于区域性稠油数据的经验式[11],这些经验式只对特定区域特定组分的稠油才有很高的预测精度,能否被应用于重质船用燃料油的黏度预测值得研究。
1.1 Arrhenius黏度模型
Arrhenius黏度模型[式(1)]是国际通用的黏度调合计算模型,被推荐用于计算混合原油的黏度[12]。该模型是建立在高黏度比的基础上,在计算稠油和轻质油混合黏度方面表现较好[13]。
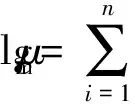
(1)
该模型的缺点是对低黏度比或混合油中含有过多沥青质沉淀体系的计算精度不高[14]。重质船用燃料油的调合体系中,调合组分一般在3种或3种以上,且有2种或2种以上的组分黏度较为接近。另外,重质船用燃料油的残渣型调合组分油,往往有某些组分的沥青质含量相对较高,如渣油、煤柴等,在计算过程中会导致偏差较大。因此,该模型在重质船用燃料油的黏度预测上存在一定的局限性。
1.2 双对数黏度模型
双对数模型[式(2)]是美国标准局的黏度调合计算模型[15],广泛应用于混合油品的调合,在目前的重质船用燃料油的实际调合生产中,该模型应用最多。但该模型不适用于计算非牛顿流体混合油的黏度,以及组分油黏度指数差距较大的混合油黏度。另外,有研究[16]表明,其计算黏度会随低黏度原油比例的变化而改变。

(2)
在重质船用燃料油黏度的预测计算中,经常使用双对数模型的变型式[式(3)]计算黏度系数υi,50。
υi,50=19.20+33.5lglg(μi,50+0.85)
(3)
假设组分油的黏度系数是呈线性关系,则混合油品的黏度系数计算式如式(4)所示。
(4)
可以利用υm,50和式(3)反推出50 ℃时的混合油运动黏度μm,50。
虽然该模型在重质船用油的调合生产中应用较多,但是一般是忽略了组分油中的非牛顿流体,因此计算中存在一定的误差。但对于黏度差距较大的重质船用燃料油的调合组分来说,该模型的预测能力具有一定的参考价值。
1.3 Cragoe黏度模型
Cragoe黏度模型[式(5)~式(8)]提出了一种表征流体流动性能的流函数概念,并在试验数据的基础上认为流函数L是具有加和性的[17]。Cragoe黏度模型不仅适用于低黏度混合油,还适用于稠油与稀油黏度比值大于1×103的系统[12]。因此对于稠油掺稀后的黏度可用该模型计算。
(5)
(6)
(7)
(8)
重质船用燃料油与原油调合最根本的区别在于组分油含有黏度较大的劣质油,这使得很多黏度模型用于重质船用燃料油的黏度预测时准确性差。而Cragoe黏度模型区别于其他物理模型的优点是它适用于各种黏度比的体系[18],但是否对多组分的残渣型重质船用燃料油调合适用仍待进一步考察。
1.4 Bingham黏度模型
Bingham黏度模型[式(9)]是将黏度的概念与电阻概念类比,结合试验数据发现黏度的倒数是有加和性的,于是提出了以倒数混合规则为基础的黏度预测模型[19]。
(9)
Bingham黏度模型的研究目前还比较少见,该模型对多组分油品调合的适配性仍需要大量的试验来考察。作为一种对非牛顿流体黏度的预测模型,可通过试验数据的对比来进一步讨论其在重质船用燃料油调合中应用的可能性。
2 模型筛选
2.1 原料油性质
选用常用的重质船用燃料油调合组分(水上油、页岩油、煤柴、渣油和油浆)进行调合试验,分别测量各组分油在50 ℃时的运动黏度等基本性质。重质船用燃料油的7种常用调合组分油的基本性质见表1。采用逆流黏度法测量混合黏度,同时应用上述各模型进行黏度预测值的计算,并对结果进行对比分析。
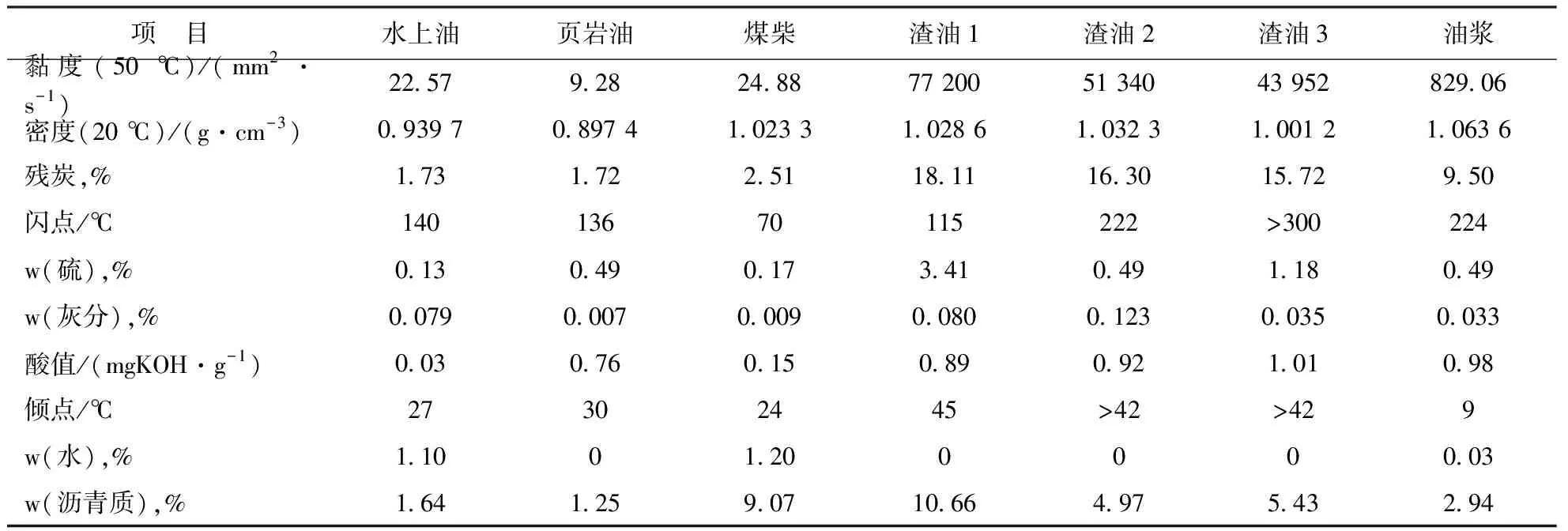
表1 重质船用燃料油的7种常用调合组分油的基本性质
2.2 模型筛选方法
采用相对误差对模型的预测结果进行准确性评价。相对误差(R)指试验测量值(μexp)与预测计算值(μcal)之差的绝对值相对于试验测量值的比例,其计算式如下:
(10)
由于渣油的黏度远远大于其他几个组分油的黏度,故选用3种渣油作为大黏度组分油,选用水上油、页岩油和煤柴作为稀组分油(简称稀油),进行了12组调合试验(所得混合油样品分别记作1号~12号),所采用的调合比例如表2所示。试验考察采用相同比例的渣油进行调合时各模型对黏度预测的准确性,渣油比例增加时对预测准确性的影响以及不含大黏度渣油时模型预测的准确性。
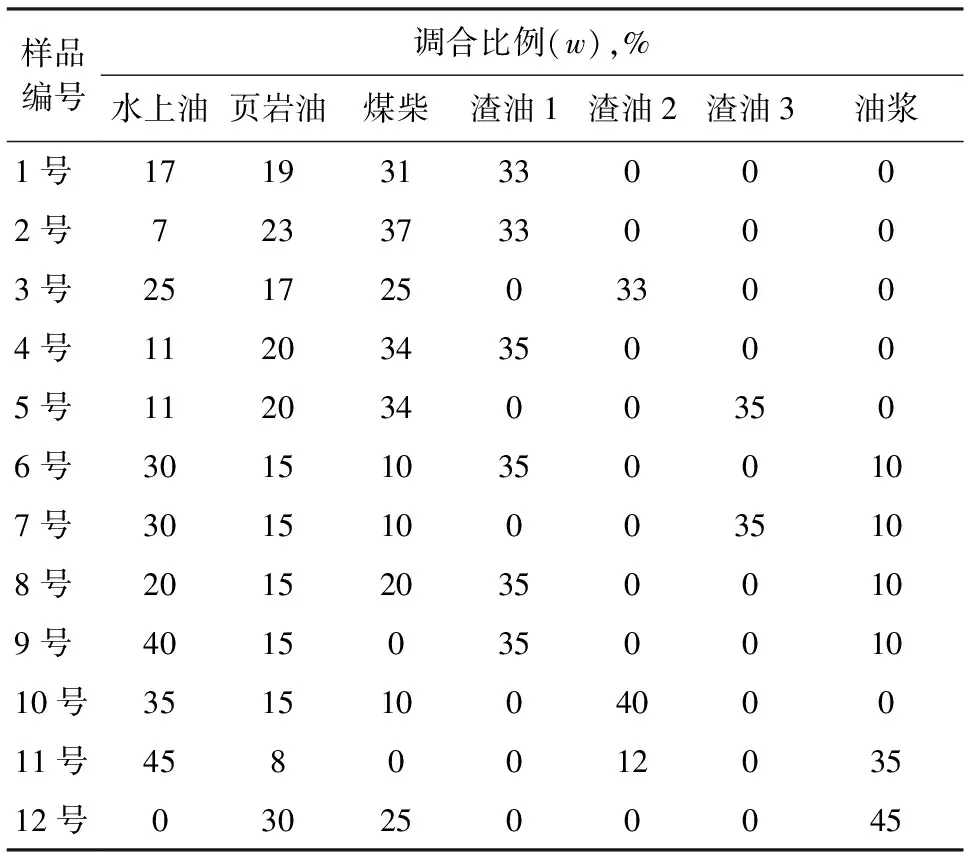
表2 调合比例
2.3 模型对比
分别采用Arrhenius黏度模型、双对数黏度模型、Cragoe黏度模型以及Bingham黏度模型对1号~12号混合油样品的黏度进行预测,并与实测黏度进行对比,结果如表3所示,模型预测的相对误差如图1所示。
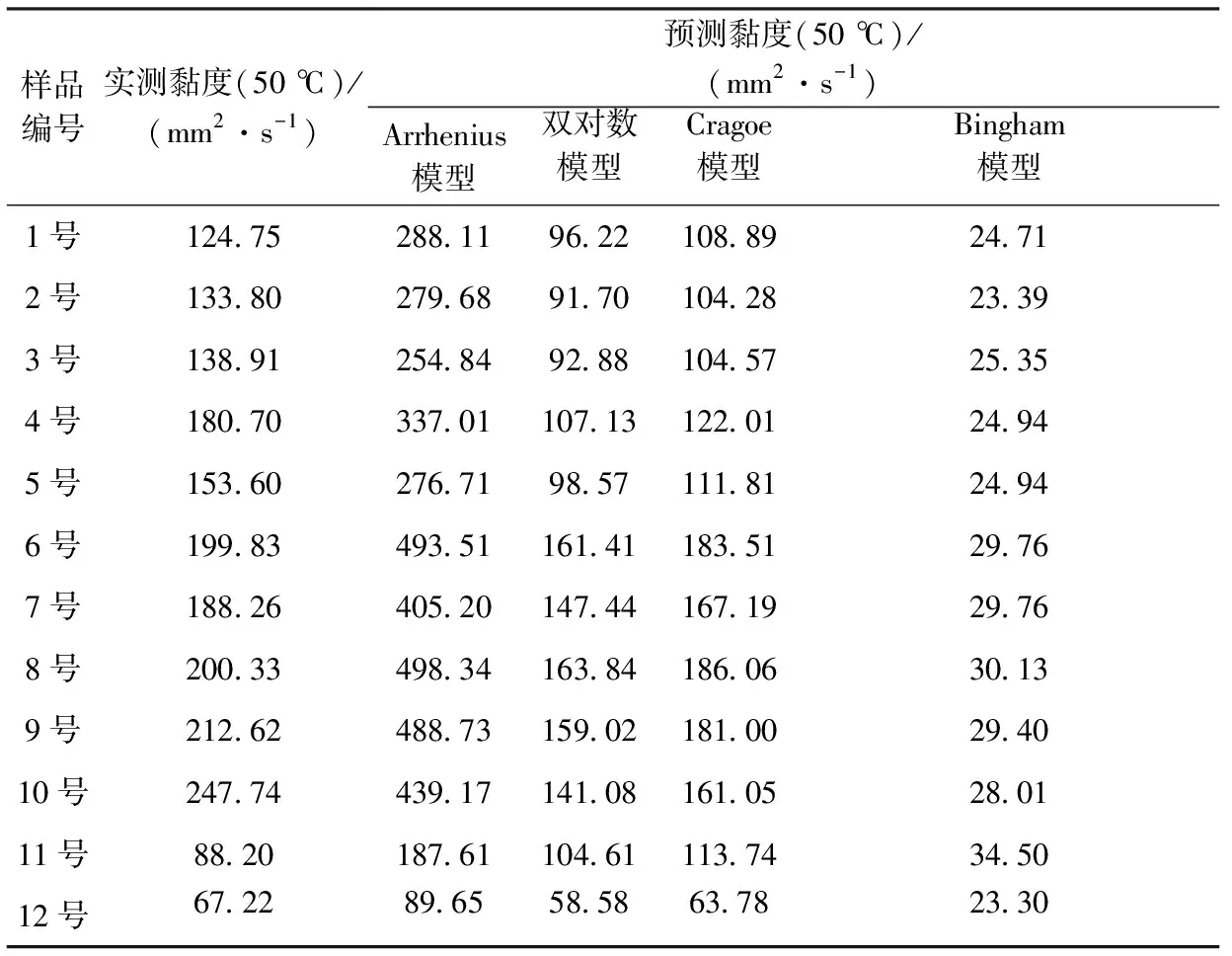
表3 实测黏度与模型预测黏度的对比
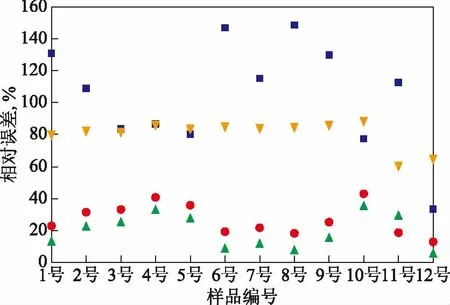
图1 4种模型预测的相对误差■—Arrhenius模型; ●—双对数模型; ▲—Cragoe模型; 模型
由表2和表3可以看出,使用黏度达到104数量级的渣油进行调合时,增加2百分点的渣油使得调合油的黏度增加50~90 mm2/s,这对物理模型的适用能力是很大的考验。
从图1可以看出:Cragoe模型的预测结果最优,相对误差较小,为5.1%~35.0%,相比其他模型,Cragoe模型更适用于这种具有大黏度比的调合体系;双对数模型的预测趋势和Cragoe模型大体一致,但相对误差略高一些,为14.3%~43.9%;而Arrhenius模型和Bingham模型的预测相对误差都很大,均在60%以上,说明这两种模型不适用于具有高黏度劣质组分的重质船用燃料油调合指标预测。Cragoe模型和双对数模型的相对误差变化趋势接近,这是因为两种模型均采用了将组分油黏度进行对数变换,利用对数的形式进行拟合形成一个黏度的相关系数,该系数呈线性加和关系,利用相关系数线性加和得到混合黏度系数,从而反推混合黏度。两个模型从建模原理上是相近的,因此对于预测的相对误差变化趋势也较为接近。从总体相对误差小的角度来说,在重质船用燃料油的调合中,计算黏度的物理模型优选Cragoe模型。
2.4 Cragoe模型修正
选取最优模型Cragoe进行修正优化以进一步降低预测的相对误差。目前文献中对Cragoe模型的修正方法均引入了质量比或体积比为1∶1时的混合油黏度μjk,修正后的模型如式(11)~式(15)所示[20]。
这种方法增加了试验量,对于重质船用油生产企业来说无疑增加了油品生产周期,应用较难。针对新疆某混合原油,研究人员根据试验数据建立了Cjk与2种组分原油黏度函数间的经验关系,引入Cjk得到修正模型Ⅱ,其中Cjk按式(16)计算[18]。
Cjk=0.030 2(Lj+Lk)-16.240 4
(16)
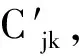
(17)
(18)
(19)
(20)
利用重质船用燃料油调合数据库内的28组调合数据对Cragoe修正模型Ⅲ进行校验,结果发现对于一般重质船用燃料油的调合体系,预测黏度的相对误差范围为0.01%~26.5%;当样品黏度过低或黏度不超过10 mm2/s时,相对误差变大,说明针对重质船用燃料油的黏度范围,该模型具有很好的预测效果。
选用重质船用燃料油调合数据库外的4个调合方案,使用Cragoe模型系列(Cragoe模型、Cragoe修正模型 Ⅱ 和Cragoe修正模型Ⅲ)进行黏度预测和误差分析,其中,调合组分新增加氢油浆(50 ℃黏度为245.50 mm2/s)、切割渣油(50 ℃黏度为299.80 mm2/s)以及更低黏度的C9(50 ℃黏度为2.78 mm2/s)和C10(50 ℃黏度为1.82 mm2/s)组分,所得混合油样品分别记作13号~16号,具体调合方案如表4所示,预测结果如表5所示,预测的相对误差如图2所示。
从图2可以看出,Cragoe修正模型Ⅲ具有较低且稳定的相对误差,相比Cragoe模型和Cragoe修正模型Ⅱ对于多组分大差异油品的混合黏度预测具有更好的准确度。但Cragoe修正模型Ⅲ在黏度过低的情况下,相对误差会略有升高,在实际黏度(50 ℃)达到30 mm2/s附近,相对误差比Cragoe模型要高。这主要是由于该模型的拟合优化主要基于重质船用燃料油数据库,重质船用燃料油数据库的黏度(50 ℃)范围一般在70 mm2/s以上,因此混合黏度过低时,模型的预测误差偏大,黏度(50 ℃)在70 mm2/s以上时具有较高的预测准确性。
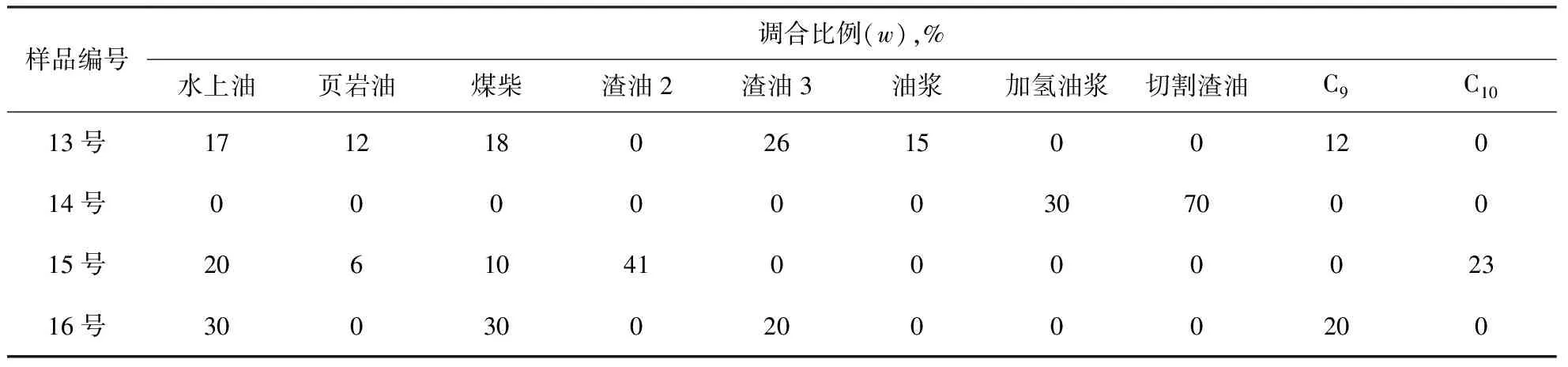
表4 Cragoe模型系列验证方案的调合比例
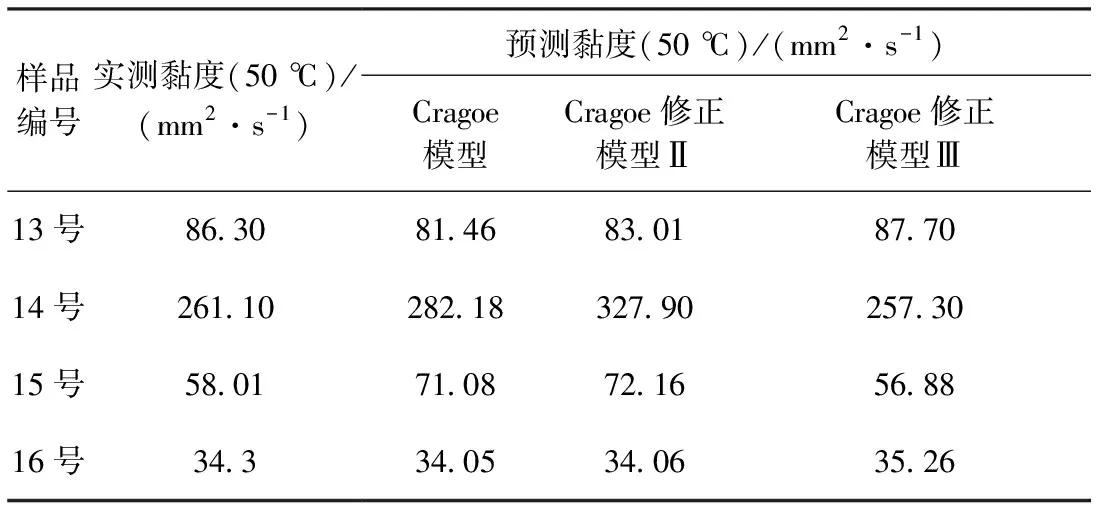
表5 Cragoe模型系列验证方案的实测黏度与预测黏度对比
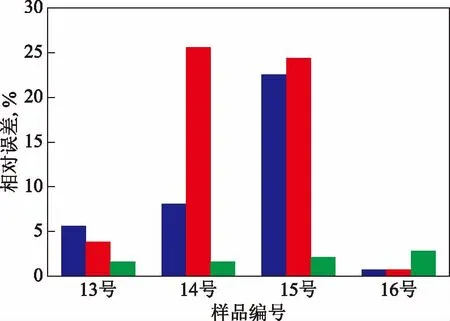
图2 3个模型的相对误差■—Cragoe模型; ■—Cragoe修正模型Ⅱ; ■—Cragoe修正模型Ⅲ
2.5 混合机制对预测误差的影响
值得注意的是,对比1号和2号、4号和6号样品发现,黏度大的组分油比例不变时,低黏度组分油比例增加会引起相对误差变大,这是因为在物理模型的计算中,低黏度组分的比例变大势必引起计算黏度值的减小。而实际调合过程中,页岩油和煤柴的比例虽均有增加,但是考虑体系中掺稀降黏会产生一定的络合效应[20],黏度没有呈下降趋势,反而因煤柴比例的增加使得混合黏度略有增大,因此导致了物理模型预测误差变大的现象。12号样本中使用油浆取代渣油后,使得体系最大黏度比的数量级从104缩小到102,相对误差大幅减小至5.1%。说明调合组分的黏度越接近,在调合时由黏度差产生的预测误差就会越小,使得模型的预测准确性越高。另外,同12号样品相似的6号~9号和11号调合样品中,同时使用了渣油和油浆,模型的计算误差都有所降低。这是因为在黏度预测模型的计算中,组分油黏度的分布范围从10~1×102到1×102~1×104形成了一个梯度式混合,而非10~1×104的断崖式混合,亦即变相减小了体系的黏度比。但其中11号样品不同于其他样品,其属于低黏度样品,混合配比中稀油组分占主体地位,在模型预测时,稀油黏度过小导致混合黏度对其比例增大的影响不敏感,因此计算结果会偏大。
根据模型计算结果可以看出,决定模型预测准确性的因素主要是大黏度渣油在调合中对黏度的影响,因此,分别采用渣油1、渣油2、渣油3与稀油进行两两调合,测量调合油品在50 ℃时的逆流黏度,建立大黏度渣油与稀油的稀释黏度关系,分析渣油掺稀后黏度下降的趋势及原因。图3所示为3种渣油分别与煤柴、水上油、页岩油这3种稀油在不同掺稀比下调合时混合油黏度与掺稀比的关系曲线,其中掺稀比为稀油与渣油的质量比。
从图3可以看出,煤柴在与渣油的掺稀比小于0.3的时候,渣油的降黏速率很小,当掺稀比超过0.3后,渣油的黏度会出现急剧下降,掺稀比超过0.4后,降黏速率趋于稳定;而页岩油和水上油添加后,渣油的黏度迅速降低,当掺稀比达到0.4后,渣油黏度基本稳定下降。由油品的组成可以看出,渣油与煤柴的沥青质较多,煤柴的加入会使潜在的沥青质发生络合反应[21],使黏度的下降趋势不如页岩油和水上油明显,因此在渣油比例不变,煤柴的比例增加后,势必使得页岩油或水上油的比例减少,渣油的稀释效果不明显,而使黏度出现了增加;另一方面,对于11号样品这样的稀油体系,在实际混合中,由于稀油对稠油的掺稀比例已经增加到很大,因此实际黏度会迅速降低,这与上述混合试验的结果吻合。
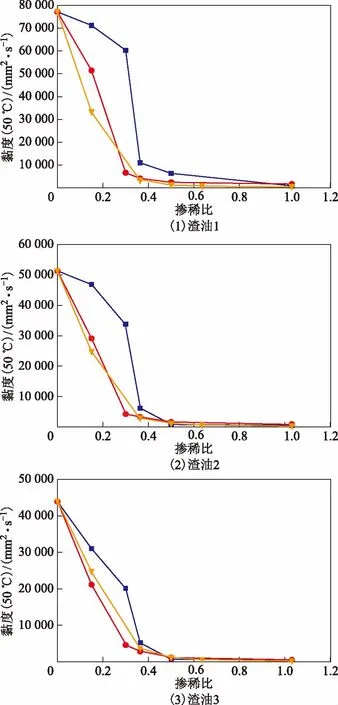
图3 3种渣油分别与3种稀油调合时混合油黏度与掺稀比的关系■—煤柴; 页岩油; ●—水上油
3 结 论
从模型的对比结果来看,物理模型计算一般均具有一定的局限性,对于重质船用燃料油的黏度预测来说,由于船用燃料油组分油的物理性质特殊性以及可能存在较大的黏度比,Cragoe黏度模型表现出了很好的适应能力以及相对较高的预测准确度。提出针对重质船用燃料油调合的黏度预测模型——Cragoe修正模型Ⅲ,该模型基于重质船用燃料油数据库拟合参数,预测准确度得到了提高,尤其黏度(50 ℃)在70 mm2/s以上时,预测的相对误差较小。分析组分油对黏度模型的影响机制可以看出,渣油黏度的数量级影响模型的预测准确性,组分油之间的黏度越接近其误差越小。同时,在大黏度渣油中加入稀油来降低黏度时,两者之间可能存在沥青质的络合效应,使得混合黏度在一定范围内的下降趋势不明显。
符号说明
Cjk——Cragoe修正模型Ⅱ的修正常数;
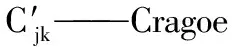
Lm——混合油品的流函数值;
Li——组分i的流函数值;
Lj——组分j的流函数值;
Lk——组分k的流函数值;
Ljk——组分j和组分k按照1∶1混合时的流函数值;
mi——组分i在调合油中的质量分数,%;
mj——组分j和组分k按照1∶1混合时组分j的质量分数,%;
mk——组分j和组分k按照1∶1混合时组分k的质量分数,%;
n——组分油个数;
R——相对误差,%;
μm——混合油品在某温度下的运动黏度,mm2/s;
μi——组分i在同温度下的运动黏度,mm2/s;
μi,50——组分i在50 ℃下的运动黏度,mm2/s;
μjk——组分j和组分k在同温度下按照1∶1混合时的运动黏度,mm2/s;
μexp——试验测量运动黏度,mm2/s;
μcal——预测计算运动黏度,mm2/s;
υm,50——混合油品在50 ℃下的黏度系数;
υi,50——组分i在50 ℃下的黏度系数;
φi——组分i在调合油中的体积分数,%。
