对“阶段考试”命题的忧虑与批判——从一个学生期中考试后的反思说起

☉江苏省盐城市初级中学 孙 峰

期中考试结束之后，学生（有时也包括教师）常常是几家欢喜几家愁，教师的不良情绪多数会“撒”到学生身上，比如，让学生写书面反思或小结就是不少教师“喜欢”做的期中分析.本文先引用一个优秀学生期中考试后的反思，再对当前的期中或期末命题工作提出一些思考或建议.

一、从学生期中考试后的一份反思小结说起

学生小Y期中考试位于班级前三名，得分接近满分，以下是小Y在期中考试之后的反思小结.

本次期中考试，试卷有点难，我被扣了3分，还不算最后一题，却都不是我应该扣的.

就说令我印象最深的选择题吧，题目如下：

某车间有27名工人，生产某种由一个螺栓套两个螺母的配套产品，每名工人每天平均生产螺母16个或螺栓22个，设应分配x名工人生产螺栓，其他工人生产螺母，才能使每天生产的螺栓和螺母正好配套，所列方程正确的是（ ）.

A．22x=16（27-x） B．16x=22（27-x）

C．2×16x=22（27-x） D．2×22x=16（27-x）

这道题是让你在读完题目后选一个与题意相符合的方程，我眼睛眨都没眨，直接选了D.这明明是正确的答案，我却留了个“心眼”，然后，一失足成千古恨.

我将D选项结果求出来，立刻发现不对劲，结果是个小数.可问题中设的是人数啊？

我反复验算了其余几个，发现只有C选项算得的是整数，我开始有了改答案的念头.

时间充足，再算，我此刻正反复验算着——我先是重复确认答案是否正确，当确保完全正确后，我将答案纷纷代入原题进行检验，发现没有一个是对的，我彻底慌了！感觉自己浪费了时间.

经过反复挣扎，我没有相信原来的自己，选择了C，结果错了，失2分！

简评与思考：如果不是看到这位优秀学生小Y的考后反思，教者本人也没有意识到这个应用问题竟然是“无解”的（所列方程有数学问题上的解，但并不符合问题情境）.学生因为思考更加深入，而陷入了纠结，结果忘了考题的设问是只要列出方程，造成不应该的失分.然而作为教师或命题者，是不是更应该反思，我们鼓励学生深入思考，但是学生因为“想得更深”“思考更全面”而受到“挫伤”，这样的试题（命题）是否值得反思呢？

二、关于阶段检测或期中（末）命题的进一步思考

1.阶段命题涉及考试范围“全样本”学生，要抵制“拿来主义”

当前初中阶段的考试密度仍然是每学期1至2次“月考”（有些学校为了回避“月考”字样，用所谓的“阶段考试”“单元练习”之类的说法，本质上是全校范围内的或者一定区域内的联考），1次期中考试，1次期末考试，其中“月考”“期中”考试的命题多是以学校为单位组织的命题与“统考”，这类命题质量最低，往往是一两个老师在较短时间内完成的，只要检索一些学科试卷网站，就能看出这类试题质量之低劣，绝大多数是通过简单的复制、粘贴而成，有些甚至直接由一些“组卷网”快速生成，加之审校不严（甚至有些学校没有审卷环节），这类试题的质量往往难以保证.笔者认为，作为全校层面的大考，涉及考查范围内的“全样本”学生，这类考卷的命制质量与影响远远超出一节大型公开课，因为就是一节省、市级公开课，影响面也往往只是一个班40~50个学生，而这种阶段检测、期中检测，影响面少则近千名学生，多则上万名学生，这些学生的老师、家长都在关注和研究这份试卷，如果这份试卷低劣不堪，不但诊断与评价功能不能实现，而且影响学校的“软实力”与教研形象.

2.教材改编题要注意试题结构，确保数据之间的自恰性

就当前的教学现状来看，以“习题单”式导学案取代教材（课本）的教学不在少数，而所谓导学案中的习题，多是网上随处可下载的一些来自全国各地的中考试题，中国每年产生几百套中考试题，成千上万份县区期末试卷，一些学科试卷网上的百万道试题，如果直接使用，师生必然在题海中挣扎，“离开教材搞教学”渐成风气.我们认为，阶段考试、期中和期末考试必须把“以本为本”作为命题第一导向或原则，在改编教材例、习题作为考试用题时，注意深刻理解教材例、习题的“深层结构”，改编数据或字母之后要确保数据之间具有自恰性，即不能破坏问题的实际意义，上文中学生小Y提及的这道选择题就属这类问题.将教材一道例、习题改编之后，虽然作为选择题，似乎仍然有选项支持答案，但是改编者没有深入思考这个方程的解，而学生却在考场上解方程，并得出非整数解的矛盾，引起了思路上的纠结，使得该题作为一道考题的“分数信度”失真，即想得更深，反而失分.这当然并不是命题者的主观意图，要想避免，就需要加强审算，深入思考数据与实际问题之间的和谐与一致.

3.原创或自编题要加强审算，防止出现结构不良型试题

用心的命题教师往往都会在一份试卷中设计2至3道原创的、自编的把关题，对这类试题需要加强审算，防止出现结构不良的试题，影响考卷质量.以下结合几道考题具体评说.

考题1：一种商品售价为2.2元/件，如果买100件以上，超过100件部分的售价为2元/件．某人买这种商品共花了n元．这个人买了这种商品多少件？

命题者给出的参考解答：

简评：这道考题要求的是商品件数，而题干中给出了参数n，这里需要明确求解要求，即设问调整为“这个人买了这种商品多少件？（用含n的式子表示）”.

考题2：（某校七上期中试卷，最后一题）如图1，数轴上点A、B分别对应数-10和8，点P从A点出发以每秒3个单位的速度沿数轴向右匀速运动，点Q从B点出发以每秒2个单位沿数轴向左匀速运动．设运动时间为t秒（t>0）．

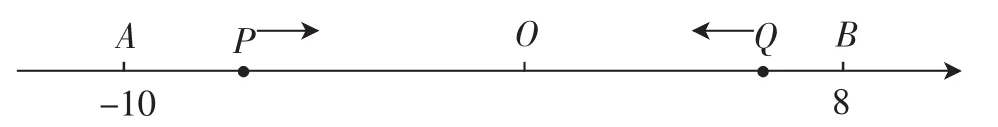
（1）当P、Q两点相遇时，求t的值和P点所对应的数.

（2）点M在数轴上，点M到P点和Q点的距离分别为x、y．

①当x=y时，如果点M与原点重合，且点P、Q不重合，求t的值；

②当x=2y时，直接写出点M的运动方向和运动速度．

命题者给出的参考解答：（限于篇幅，这里只给出最后一问的答案）

由题意可知：P对应的数为-10+3t，Q对应的数为8-2t.

②设M对应的数为m，则x=|-10+3t-m|，y=|8-2t-m|.结合条件x=2y，所以|-10+3t-m|=2|8-2t-m|，则-10+3t-m=2（8-2t-m）或-10+3t-m+2（8-2t-m）=0.解得m=26-7t或

简评：这道试题前两问比较常规，最后一问有些莫名其妙，虽然命题者给出了所谓的解答，但这种答案是“想当然”的思维定式，具有很多“潜在假设”，比如，点M从何处出发？规定点M向右运动为正，向左运动为负.而这些运动的关键信息在题目的条件中都没有给出，是一道结构不良型试题.“极端”一点，可类比网传的那道“已知船上有羊26只，小艇10条……求船长的年龄.”顺便指出，当前这类以数轴为平台研究单动点、双动点甚至多个动点的问题渐渐成为“网红题”，似乎成为七年级上学期期中、期末考卷中的必考题，这种“网红题”的大量传播应该得到应有批判和抑制.教材上没有用数轴来研究动点的题型，数轴的价值是研究数与形的一一对应，是数形结合的工具，而不是作为动点问题的平台，很多动点问题本质上都是线段和差、倍分，以及行程问题（相遇与追及）的综合题.而这些考查已远离了数轴的教学价值，成为一类“伪数轴”试题.

三、写在后面

翻阅中学数学教学类专业期刊，对于考题、考卷的赏析（更多的是标签式吹捧）很多，然而有质量的命题批判与商榷改进少之又少，这不能不说是一种遗憾.如同文学艺术一样，缺少高质量的文学批评的参与，文学研究难以繁荣.我们期待着面对成千上万套的月考卷、期中考试卷，商榷与“批评”的相关研究也能积极跟进，以加深我们对考试研究的理解，也能端正和倒逼命题者更加审慎地对待命题工作.