想清辨明定义结构，铺垫设问变式反馈——以北京海淀九上期中卷新定义考题为例

☉广东省广州市花都区炭步镇炭步初级中学 汤妙娟

新定义考题是目前各地中考、期中、期末考试的热点题型，也在各级复习备考活动中占据重要位置，但是新定义考题的类型是丰富多样的，其中北京市中考引领下的一类涉及隐圆、动圆的新定义考题风格独特，体现了少算多思、构思要求高等特点，值得关注.本文结合北京海淀区2018年11月九上期中卷一道新定义考题，谈谈如何围绕一道新定义考题开展“一题一课”的教学设计，供分享和研讨.

一、新定义考题及思路解析

考题：（2018年11月北京海淀区）在平面直角坐标系xOy中，点A是x轴外一点，若平面内的点B满足：线段AB的长度与点A到x轴的距离相等，则称点B是点A的“等距点”.

（1）若点A的坐标为（0，2），点P1（2，2）、P2（1，-4）、

（2）若点M（1，2）和点N（1，8）是点A的两个“等距点”，求点A的坐标.

思路解析：（1）在平面直角坐标系中画出草图，如图1，容易求出AP1=AP3=OA=2，所以点P1、P3是点A的“等距点”.从“结构”上看，可以作出一个半径为2的圆A，此时圆A恰与x轴相切，并且点P1、P3恰在圆A上.

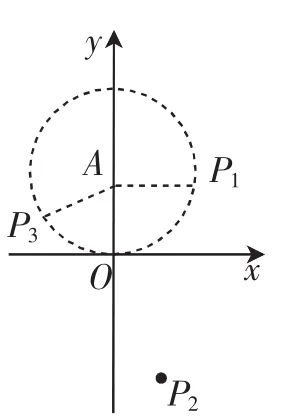
图1

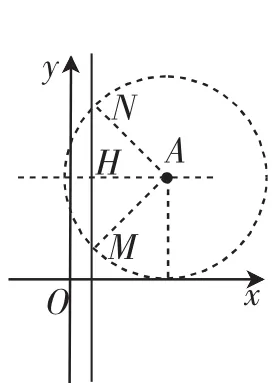
图2

（2）先构造图2分析，MN//y轴，且MN=6，结合M、N都是点A的“等距点”，可知点A应该在线段MN的垂直平分线上，同时点A到x轴的距离也与AM、AN相等，可构造圆A与x轴相切，且点M、N恰在圆A上，此时圆A的半径为5.构造直角三角形AMH，利用勾股定理可求出AH=4，于是点A的坐标是（5，5）.根据对称性，可知在第二象限有另一点A′与A关于直线MN对称，也是符合要求的，即A′（-3，5）.综上，点A的坐标为（5，5）或（-3，5）.

（3）先作出图3进行分析，此时点M到x轴的距离为MH，点M到圆上一点的距离的最小值是MN，连接MT交圆T于N，此时MN小于MH.可以调整N点的位置使得MH=MN，这样就符合“等距点”要求.

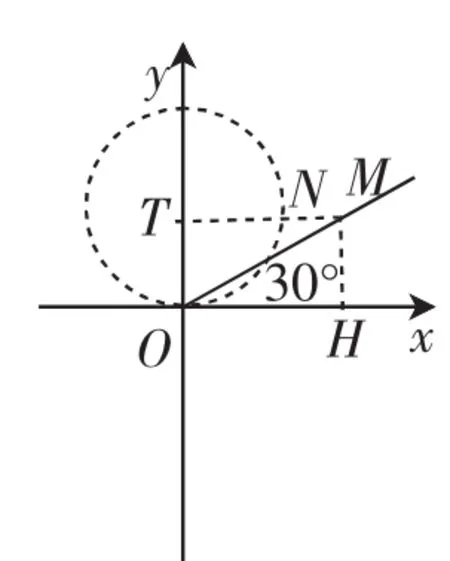
图3

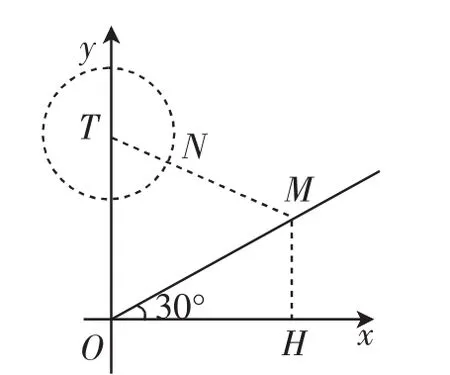
图4

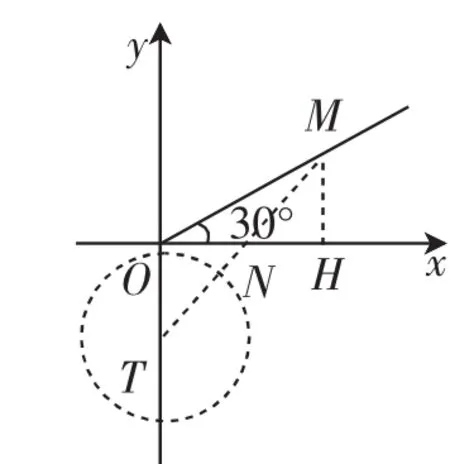
图5

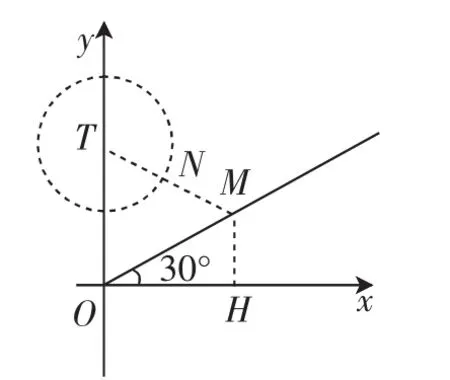
图6

接下来构造图4，这种图形位置情况下，点M到圆上一点的最小距离MN大于MH的长，不符合“等距点”要求.类似的，构造图5，当圆到了x轴下方，与x轴无交点时，MN一定大于MH，也不符合“等距点”要求.

一个临界状态就是当圆心T在y轴的负半轴上时，圆T与x轴相切的位置关系，即t>-2.（注意，由于x>0，所以

再构造图6，分析出另一临界状态，当△TOM恰构成等边三角形时，此时MN=MH.结合OT=OM=TM=t，于是MN=t-2，而在Rt△OMH中，MH=0.5t.当t-2=0.5t，即t=4时，相应的求出该等边三角形边长为4，满足题意.故t≤4.

综上，-2

解后反思：从上述求解来看，关键是理解新定义“等距点”的图形结构，从第（1）问开始，就会有一个隐性的圆贯穿问题探究的全过程，前两问中的圆都是一个“确定”的圆，位置固定，而第（3）问中的圆是一个动圆，其圆心在y轴上上下平移，能否想清圆在上下平移过程中的两处临界位置成为解题的难点与关键所在.

二、围绕考题设计的解题微教学

教学环节（一） 熟悉定义

给出“等距点”定义后，教师可结合平面直角坐标系，举例帮助学生理解，然后安排学生在小组内互相举例，加强对定义的理解.然后给出以下小问：

问题1：若点A的坐标为（0，2），判断点B（2，2）、C（1，-4）是否为点A的“等距点”，并说明理由.

问题3：请判断E（1，4）是否为点A的“等距点”.如果是，请说明理由；如果不是，能否将点E适当平移，使之成为点A的“等距点”？

教学环节（二） 初步运用

例1 若点M（1，2）和点N（1，8）是点A的两个“等距点”，

（1）根据新定义，有人认为点A一定在直线y=5上，你觉得这种判断正确吗？说说你的理由.

（2）小睿指出，点M、N应该同时在半径为5的圆上，你觉得有道理吗？

（3）根据对称性，点A应该有几种不同的位置？结合以上分析，求出点A的坐标.

设计意图：通过几个铺垫式问题，有效化解了考题第（2）问的难点与解题障碍，想清以上3个关键步骤，就能口算得解．

教学环节（三） 挑战难题

（1）当t=1时，画出图形，并在图形中找出满足条件的一组点M、N.

（2）当t=5时，以OT为一边作等边三角形OTP，求点P的坐标.

（3）当t=-3时，能否找到符合要求的点M、N？结合图形进行分析说明.

（4）直接写出t的取值范围.

设计意图：为了让学生能想到、想清两处临界位置，设计了（1）~（3）的铺垫式问题，为的是使学生学会分析，数形结合，让圆T动起来，逐渐逼近问题的两种临界位置.

教学环节（四） 变式再练

变式题：在平面直角坐标系xOy中，点A是x轴外一点，若平面内的点B满足：线段AB的长度与点A到x轴的距离相等，则称点B是点A的“等距点”.

（1）若点A的坐标为（1，2），点P（13，2）、P（22，6）、）中，点A的“等距点”是________.

（2）若点M（1，2）和点N（1，6）是点A的两个“等距点”，求点A的坐标.

三、进一步的思考

1.深刻理解新定义考题，需要想清新定义的本质

新定义问题往往都是基于初中阶段所学过的一些概念发展而来的，这时结合新定义所举的图形或例子，想清辨明新定义的本质所在，新定义所对应的图形结构或某种基本图形，是后续问题求解的关键.事实上，这也是我们在概念教学时应该注意的一个薄弱点，即章建跃教授所批判的“一个定义，三项注意，大量练习”式的数学概念教学对学生理解数学造成的“伤害”.像上文新定义考题第（3）问的本质就是圆T（半径为2）在y轴上上下平移，寻找两个位置符合题意，相应找到两个临界值.

2.开展新定义考题教学，需要预设铺垫式问题

新定义考题的教学不能只是拿着一道题就从前讲到后，而要对试题的呈现方式做出必要的变式改编，上面我们给出的就是通过分解步骤，预设铺垫式问题，以问题串的方式推进教学进程，这需要教师在课前精心准备，特别是教师需要具备一定的命题改编能力.在预设铺垫式问题时，还要注意贴近原考题的设问方向，不能离“题”太远，偏离原设问的设问或变式不宜出现.讲评最后，为了检测学生的理解情况，还可对原考题整体上进行简单的变式改编，如上文课例中的环节（四），就是针对原考题对各个小问进行了简单的数字或符号的变式，并没有破坏原题的设问本质与问题结构，侧重考查学生对考题的掌握程度.