再谈垂径定理及其应用
2019-03-15湖北省武汉市第三十中学
☉湖北省武汉市第三十中学 程 艳
初中九年级的学生在七、八年级时已经学习了轴对称图形的有关概念和性质,也学习了等腰三角形的对称性和三角形全等的知识,本节课,要求学生在理解弧、弦的概念和了解等圆、等弧的概念的基础上,准确理解、掌握垂径定理及其推论,会进行相关计算,并会运用垂径定理及其推论解决现实生活中的问题,提升学生分析、探索和证明的能力.
课前准备好三角板、圆规等部分教具、自制课件和个人电脑.以下是垂径定理的应用这节课的课堂实录.
师:今天我们复习圆的垂径定理及其应用!请问,圆的重要性质是什么?
生1:圆既是中心对称图形又是轴对称图形.
师:根据圆的轴对称,可得圆的垂径定理,什么是垂径定理?
生2:在圆中,垂直于弦的直径平分这条弦,并且平分弦所对的弧.
教师画图示意.
师:垂径定理有哪些推论?
生3:推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
生4:推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
师:垂径定理还有哪些推论?请举手回答!
生5:推论3:平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧.还有推论4:圆的两条平行弦所夹的弧相等.
师:同学们在学习垂径定理时会碰到平分弦、优弧和劣弧,垂直于弦,过圆心等具体条件,如何有效进行推理?
师:在下列5个条件中,只要具备其中任意两个作为条件,就可以推出其他三个结论.简称为知二推三.
(1)平分弦所对的优弧;
(2)平分弦所对的劣弧;(前两条合起来就是:平分弦所对的两条弧);
(3)平分弦(不是直径);
(4)垂直于弦;
(5)过圆心.
师:垂径定理是初中数学的重要内容,同学们必须理解圆的轴对称性和垂径定理及其推论,初三数学学习中,掌握垂径定理,并能应用垂径定理及其推论进行有关计算和证明,是解决和圆有关的问题的关键.
垂径定理主要用来解决长度、角度、范围等问题,下面通过几个例子进行逐一体会:
一、垂径定理的简单运用
例1 (2018·湖南张家界)如图1,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( ).
A.8cm B.5cm C.3cm D.2cm
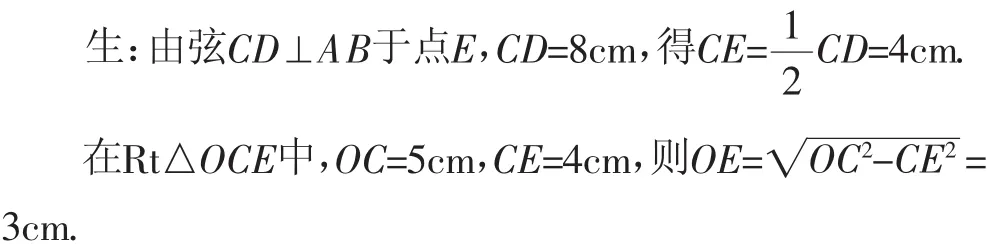
则AE=AO+OE=5+3=8(cm).
故选A.
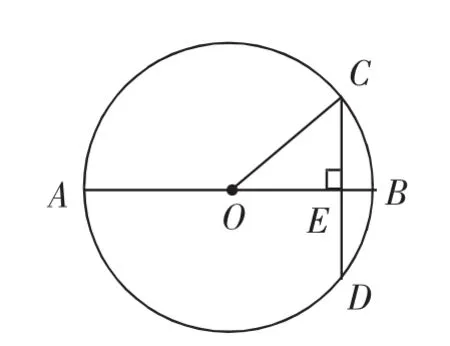
图1
图2
例2 (2016·广西百色)如图2,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=______.
生:由∠C=25°,得∠A=∠C=25°.
由⊙O的直径AB过弦CD的中点E,得AB⊥CD.
则∠AED=90°.
则∠D=90°-25°=65°.
故答案为65°.
二、利用垂径定理解决长度问题
例3 (2017·浙江金华)如图3,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( ).
A.10cm B.16cm C.24cm D.26cm
生:由OB=13cm,CD=8cm,得OD=5cm.
则AB=2BD=24(cm).
答案为C.
师:本题中没有给出垂径定理的条件,但我们可以通过作辅助线作出垂直于弦的直径,从而利用其平分弦及垂直产生的直角,借助勾股定理求出线段长度.
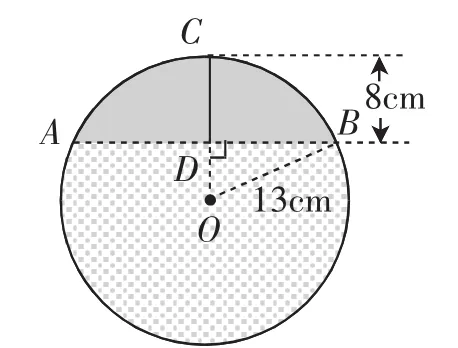
图3
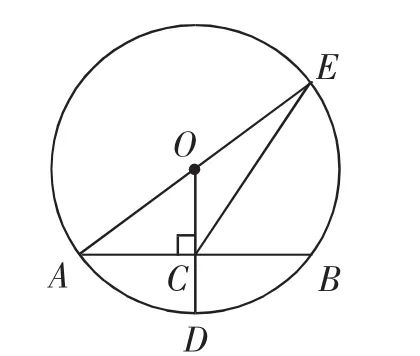
图4
例4 (2013·浙江嘉兴)如图4,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为( ).
师:观察题中是否有垂径定理模型.
生:OD垂直平分AB.
师:由垂径定理可以得到哪些量?
生:AC=4,CD=2.
师:求解线段CE的长,利用勾股定理必须构建直角三角形,如何构建直角三角形?
生:连接EB,则由直径所对圆周角是直角可知△EBC为直角三角形,由EB=2OC,BC=4,可求EC.
师:说说你的解题过程.
生:由⊙O的半径OD⊥弦AB于点C,AB=8,得AC=AB=4.
设⊙O的半径为r.
则OC=r-2.
在Rt△AOC中,AC=4,OC=r-2,OA2=AC2+OC2.
则r2=42+(r-2)2,解得r=5.
则AE=2r=10.
连接BE.
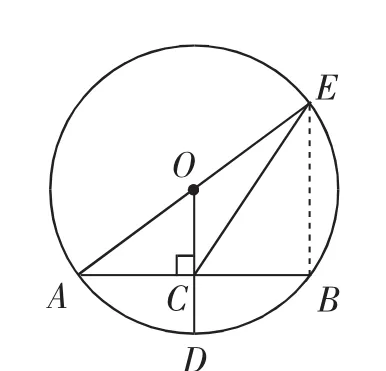
图5
由AE是⊙O的直径,得∠ABE=90°.
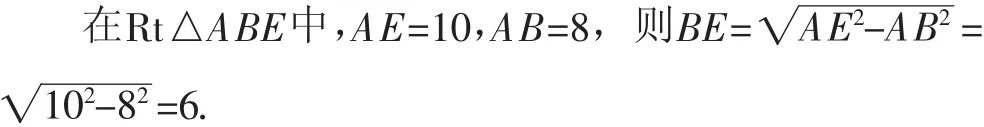
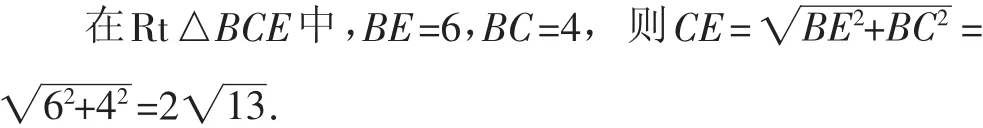
故选D.
师:解决求线段长的问题时,要充分挖掘题中条件,合理构建直角三角形,借助勾股定理求线段长.本题根据题意作出辅助线,构造出直角三角形是解答此题的关键.
三、利用垂径定理解决角度问题
例5 (2018·山东菏泽)如图6,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA等于( ).
A.64° B.58° C.32° D.26°
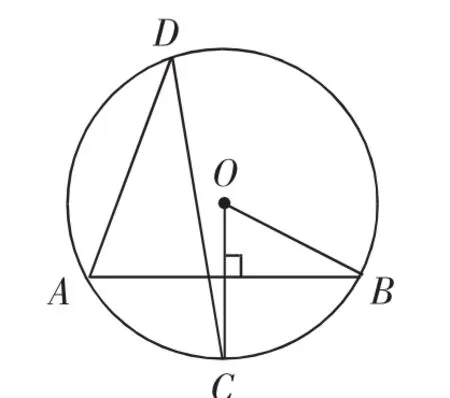
图6
生:如图7.
∠2=2∠1=2×32°=64°.
则∠3=64°.
在Rt△OBE中,∠OEB=90°,则∠B=90°-∠3=90°-64°=26°.
故选D.
师:此题考查垂径定理与圆周角定理.此题比较简单,应注意掌握数形结合思想的应用.
例6 (2017·湖北襄阳)在半径为1的⊙O中,弦AB、AC的长分别为1和,则∠BAC的度数为______.
师:根据题中所给条件画出适合的图形,大家试着画画看
生1:如图8.
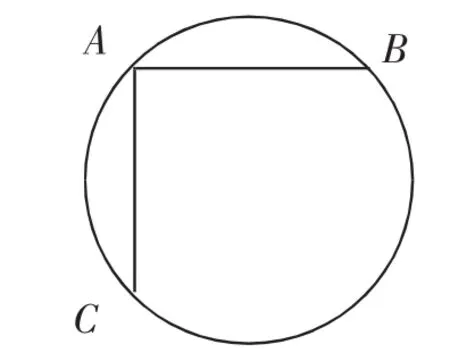
图8
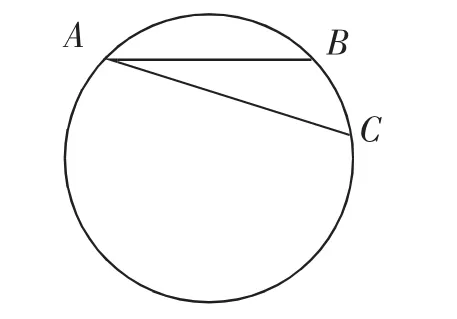
图9
师:大家认可这种图形吗?
生2:还可能是另一种情况,如图9.
师:你是如何想到有这两种位置关系的?
生3:将AC绕着点A试着旋转一下就可以发现应该有多种情况.
师:非常好!下面请大家试着算算看.
生4:按照图10的解法:

生5:如图11,当点O在∠BAC的外部时,∠BAC=60°-45°=15°.
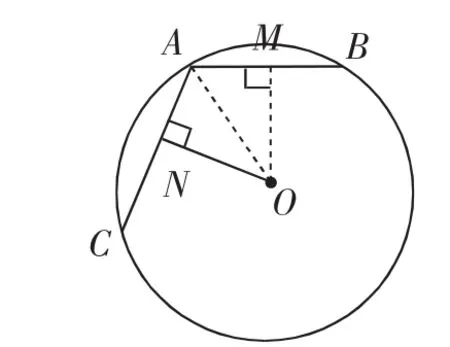
图10
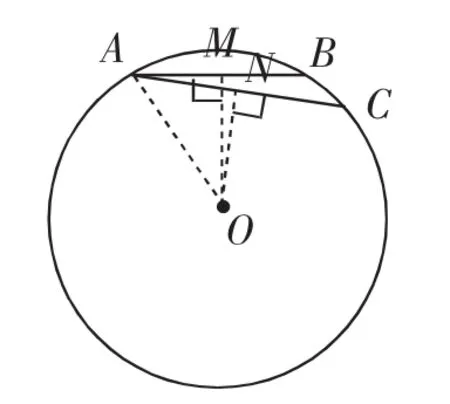
图11
四、利用垂径定理解决最值问题
例7 如图12,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上一个动点,以AD为直径作⊙O分别交AB、AC于E、F两点,连接EF,则线段EF长度的最小值为______.
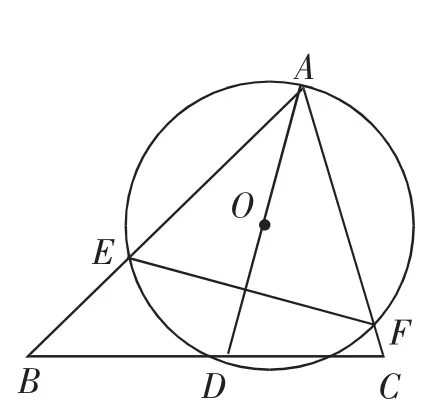
图12
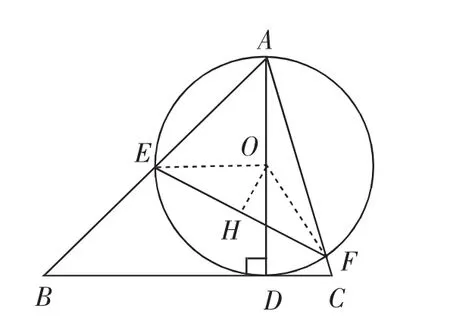
图13
师:由垂径定理我们可以发现,圆的半径、半弦长可以构成直角三角形,所以我们可以利用这个直角三角形求弦长,由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,如图13,连接OE、OF,过O点作OH⊥EF,垂足为H.在△EOF中,∠EOF=120°,OE为半径,EF=2EH=2OE·sin60°.要使EF最小,只需要OE最小.又2OE=AD,故当AD⊥BC时,AD最小,所以可求.

例8 (2015·泰兴市二模)如图14,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=a,则a的最大值是______.
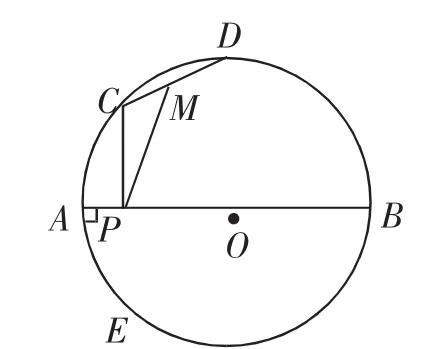
图14
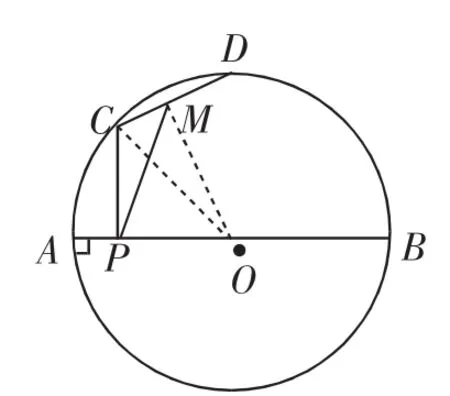
图15
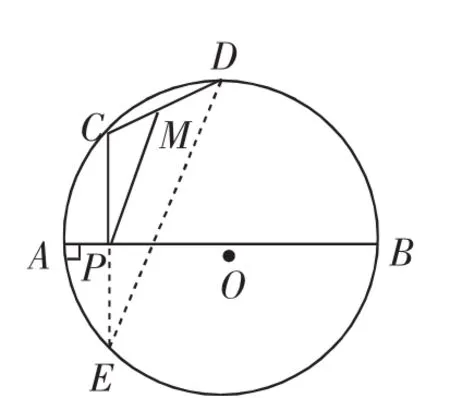
图16
生1:连接OM、OC,推出PM=OC,求出OC的长即可.
连接CO、MO,根据∠CPO=∠CMO=90°,所以C、M、O、P四点共圆,且CO为直径.设CO的中点为E,则PM为⊙E的一条弦,当PM为直径时PM最大,所以PM=CO=4时PM最大.即PMmax=4.
生2:延长CP交⊙O于点E,根据垂径定理,得P是弦CE的中点.又M是CD的中点,连接ED,则PM为⊙O的弦长ED的一半.当ED为直径时,PM的长最大,最大为直径AB的一半,则PM的长度的最大值为4.
师:本节课主要讲述了垂径定理的基本内容和垂径定理的应用.
在解决角度、长度等问题的过程中,往往需要借助圆的切线的性质,平行线的性质和判定,勾股定理,圆周角定理,圆心角、弧、弦之间的关系,能灵活运用这些知识点进行推理是解题的基本途径,大家今后在解决圆的相关问题时,要注意综合利用题设条件,合理运用垂径定理.F
