基于生活经验的“勾股定理的应用”教学设计

☉江苏省无锡市侨谊实验中学 李文杰

“勾股定理的应用”一节的教学，不但能够促进学生对基本原理形成深刻认识，而且能有效发展学生的数形结合、数学建模、方程等思想.为了达成上述目的，本文指出教师应该从学生的生活经验出发设计各种情境，提升学生的学习效率.

一、提出问题

勾股定理是一个应用性很强的数学原理，它兼具很强的代数性质和几何味道，在实际应用时，需要学生充分发挥数形结合、数学建模、方程等思想，积极发现并构建直角三角形，并从中努力发掘各边的具体特点，最终完成相关问题的解决.由此可见，“勾股定理的应用”一节的教学，不仅强调学生对知识的理解，更强调学生灵活运用数学思想和基本方法.

从实际问题中提炼出直角三角形的模型，并展开问题探究，是本节课的重点所在，因此笔者认为，教师应该充分研究学生的生活经验，并由此设计问题情境，指导学生展开探索，让学生在问题研究的过程中提升认识水平，发展相关的数学研究能力.

二、教学片段展示

1.依托学生的校园生活实施导入

教学过程中，教师要善于从学生的校园生活出发创设问题情境，引导学生展开思考.

师：每周一我们都有例行的升旗仪式，你知道我们学校的旗杆高度是多少吗？有什么方法来对它进行测量呢？通过今天有关勾股定理应用的学习，你们将能很轻松地解决这个问题.（教师通过ppt展示升旗仪式的场景）

师：之前我们已经学习过勾股定理，请回顾一下它的基本内容.

生：在直角三角形中，两条直角边的平方和等于斜边的平方.

师：不错，勾股定理说明的是直角三角形中三条边的长度关系，也就是说，结合这个原理，若已知两条边可以确定第三条边的长度.在使用这个原理进行问题分析之前，我们要明确两个问题：（1）对应三角形是直角三角形吗？（2）这个直角三角形的哪条边是斜边？实际上，勾股定理不但能够用于数学问题的分析，在生活中也有着非常广泛的应用.

2.结合典型生活实例展开探究

在指导学生运用数学原理进行应用研究时，教师要善于结合典型的生活实例创设问题情境，引导学生展开探索，并让学生在探索过程中进一步熟悉数学原理，提升问题分析能力.

片段1：初步应用.

问题情境（1）：如图1所示为一个太阳能热水器，已知其支架AB与BC垂直，且两边的长度分别为90cm和120cm，请分析真空管AC的长度.

学生结合题意展开分析，从题目情境中提炼出直角三角形模型，由此将一个生活化的问题转换为数学问题，这其实正是建模思想的训练.学生直接根据勾股定理，即可完成这个问题的求解.

问题情境（2）：如图2所示为学校的一个花圃，它是一个长方形，长和宽分别为4m和3m，但是由于部分学生调皮，喜欢避开拐角走捷径，因此就让其中间形成了一条路，请分析：这样走其实只少走了多少路？

师：通过题意的分析，你们看到了什么图形？

生：一个直角三角形.

师：哪来的直角？

生：因为花圃是长方形的，四个角都是直角.

师：不错，你能求解这个问题吗？

学生经过思考后，给出问题的解决思路和结果.教师则顺势指出：实际上，踩踏草坪也没有少走多少路，这是一种非常不道德的行为，应坚决予以制止.

片段2：逐步提升.

图1

图2

问题情境（3）：校园中的荷花池是一道美丽的风景，如图3所示，微风拂过，荷花摇曳，煞是动人.在数学史上，曾经有一个数学家通过一首小诗提出问题：平平湖水清可鉴，面上半尺生红莲；出泥不染亭亭立，忽被强风吹一边；渔人观看忙向前，花离原位二尺远；能算诸君请解题，湖水如何知深浅？

教师让学生阅读问题，要求学生提炼其中的数学信息，并给予一定的时间让学生进行深入思考.

师：请同学们结合诗的内容，将几何图形画在纸面上，并将已知条件和所求量标记在图形的边侧.

当学生完成任务后，教师将部分学生绘制的图形通过实物展台投影出来，让学生相互比对，并校准认识.

师：在上述图形中，貌似只是已知一条边，我们怎么确定其他边呢？

生：利用方程处理，设一条边为x，则另外一条边可以表示为x+0.5.

师：很好，方程思想是处理数学问题的关键性思路，请大家继续完善思路，并求得结果.

学生完成问题的分析，教师则要求学生进一步总结解题的思路和基本步骤.

片段3：能力升华.

问题情境（4）：我们还是回归导入阶段的问题，你能设法测定学校操场上旗杆的高度吗？为你提供的工具包括旗杆、升旗绳子和皮尺，请设计方案，并结合数学知识说明相关计算过程.

教师引导学生从荷花的问题中寻找启发和灵感，并安排学生进行合作探究.师：大家的讨论是否已经有结果了？请进行展示.生：将绳子拉直，然后可以构建出一个直角三角形.师：说得不够形象，你能到黑板上画出图形，并进行说明吗？

图3

生：（板演绘图）将绳子向着侧边拉，这样就可以形成如图4所示的直角三角形.

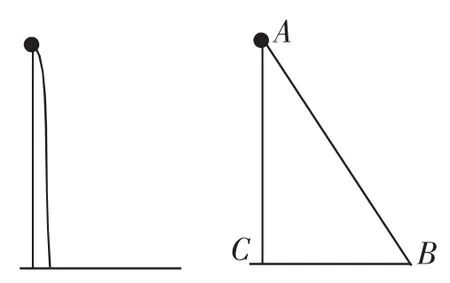
图4

师：的确形成了一个直角三角形，可是这个三角形中只能直接测定地面上的那条边，其他的边（旗杆长和绳子长）都无法测定，怎么解决问题呢？

生：可以利用方程思想，先将绳子竖直着拉，这样可以确定绳子比旗杆长多少，后边的问题处理与荷花的问题处理相似.

师：大家同意他的做法吗？

其他学生纷纷表示赞同.

3.课堂小结

师：通过本节课的学习，你有什么收获和体会呢？

学生展开总结，基本内容包括以下几点：（1）加深了对勾股定理的认识，并掌握了基本的方法；（2）对生活化的问题情境要善于提炼信息，运用数学建模完成问题分析；（3）如果直角三角形中只知道一条边的具体长度，则可以结合勾股定理通过建立方程完成问题分析；（4）运用勾股定理解决问题，关键是要发现直角三角形，如果没有现成的直角三角形，就需要构建直角三角形.

三、教学反思

如何更加有效地激活学生是教学设计最重要也是最基本的目的所在.在本课的设计中，教师从学生的实际生活经验出发，多方位设计问题情境，有效引发学生的共鸣，让学生更加主动地参与到问题的探究中来.

首先，本课的设计着眼于学生的兴趣激起，教师依据对教学内容的认识，从学生的校园生活出发，发掘有关联的教学素材，创设更加鲜活的情境，将重点内容融入其中，让整个教学更加生动且流畅，学生的学习也更加投入且主动.

其次，本课侧重于用实际问题引领学生探究，充分训练学生的数学建模能力，让学生在真实的场景中理解知识的真正价值，感受最纯粹的数学探究过程.而且在设计过程中，教师还积极贯彻“由浅入深、循序渐进”的教学原则，设计逐级提升的问题台阶，让学生充分感受问题的发展，并获得相应的提升.

最后，教师在教学过程中还遵循“不愤不启，不悱不发”的教学原理，为学生的自主思考和合作学习搭建平台，放手让学生展开深度分析和探索，当学生的思路受阻时，教师没有替代学生的思考，而是进行启发，或组织学生讨论，由此引导学生突破认识的瓶颈，实现学习的突破.在这样的课堂上，学生真正成为学习的主人，他们的能力得到了切实的提升.