对“低渗透储层存在强应力敏感”观点的质疑
2019-03-15周鹏高
周鹏高
(克拉玛依职业技术学院,新疆 克拉玛依 834000)
0 引 言
储层的应力敏感是指储层岩石的物性参数随应力状态的改变而发生变化的性质[1]。实际油气开采是一个外压不变、内压(孔隙流体压力)不断改变的过程。岩石的物性参数主要包括孔隙度、渗透率等,由于渗透率比孔隙度对产量的影响更大,矿场上一般只进行渗透率的敏感评价。应力敏感评价主要研究孔隙流体压力变化对储层岩石渗透率造成的影响。
近年来,大量低渗透油气藏投入开发,低渗透储层的应力敏感问题成为研究热点之一。石油学界开展了大量研究,但对于储层(尤其是低渗透储层)是否存在强应力敏感,一直存在2种相反的观点。部分学者[2-11]认为,随着孔隙流体压力的下降,储层岩石固体骨架承受应力大幅度增加,岩石由此产生变形,孔隙和毛细管被压缩、关闭,导致渗透率降低,储层岩石具有很强的应力敏感性。也有学者[12-16]认为,储层岩石的应力敏感与岩石的硬度、孔隙度有关,岩石越致密越难以压缩,储层岩石不存在强应力敏感。在实验测试方面,多数实验[5-11]测得储层岩石应力敏感较强,也有部分实验[15-17]测得应力敏感较弱。在油气开发生产实践中,储层渗透率的下降是由诸多因素共同作用的结果,各因素耦合作用并相互影响,现有技术手段还不能对“孔隙流体压力下降导致储层渗透率降低”(储层的应力敏感)进行单一因素的定量评价。因此,关于低渗透储层是否存在强应力敏感的争议一直未能解决。从发表文献的数量来看,认同“低渗透储层存在强应力敏感”的观点居多。笔者对该观点存在质疑,理由有三:其一,实验测试本身存在问题,实验结果难以反映岩石渗透率的真实特性;其二,进行应力敏感评价时错误选用Terzaghi有效应力,放大了储层应力的敏感程度;其三,应力敏感评价理论计算结果表明,低渗透储层不存在强应力敏感。
1 实验测试存在的问题
1.1 难以模拟储层岩石实际受力状态
实验测试时,把岩心装入封套中,封套外面施加围压,向其中注入流体,流体压力即为内压。测试多采用定内压变外压的方式进行,选定出口端压力,改变外压测量一组渗透率数值;测试也可采用定外压变内压的方式进行,即通过调节回压阀改变内压。
定内压变外压的测试方式与储层岩石实际受力状态不符,并不能反映储层岩石对孔隙流体压力变化的敏感。定外压变内压的测试方式更真实地模拟储层岩石实际受力状态,但此种方法对测试装置的精度和性能要求较高,实验风险也较大。
由于测量装置自身的局限性,所施加的外压和内压远低于实际储层岩石受力状态。根据行业标准[18],实验测试施加的外压、内压普遍偏低,测试压力变化范围小,与实际储层岩石所受的外应力和孔隙流体压力差距甚远。由于应力敏感实验中初始有效应力远小于储层岩石真实的有效应力,导致测得的初始渗透率大于地层条件下的渗透率,实验测得的应力敏感程度被放大。
薛永超[5]等选取不同级别渗透率的岩心进行了应力敏感实验对比研究,其中,样品号为CN14的岩心在有效应力为2 ~35 MPa 条件下测试的渗透率如表1所示。对测试数据进行拟合,得到渗透率-有效应力关系曲线(图1)。

表1 不同有效应力下的渗透率
由表1和图1可以看出,渗透率随有效应力增大而降低,但有效应力增大到一定程度后渗透率降幅很小。显然,有效应力为2 MPa时测得的初始渗透率远大于地层条件下的渗透率。以低有效应力条件下测得的初始渗透率为参考,必然会得出“储层岩石存在强应力敏感”的结论。在实际应力状态下,储层岩石未必存在强应力敏感。行业标准[18]规定有效应力的测点最大为20 MPa,据此得到的测试结果必然会夸大应力敏感程度。
1.2 微间隙影响实验结果
实验中将坚硬的岩心置于柔软的封套中,岩心与封套之间由于各种原因而存在微间隙。当外应力变化时,橡胶封套的变形量较岩心的变形量更大。
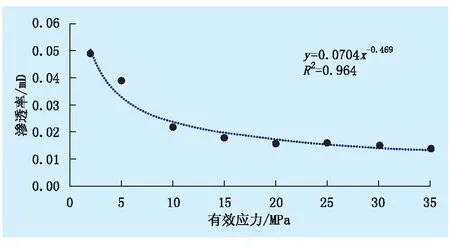
图1渗透率-有效应力关系曲线
这些微间隙对于中高渗透岩心不会产生太大的影响,但对于低渗透岩心的影响程度会增大。因此,使实验测量得到“低渗透储层岩石应力敏感强,高渗透储层岩石应力敏感弱”这样逻辑反转的结果[12-13]。
高涛等为了验证岩心与封套之间微间隙对渗透率的影响,进行了假岩心实验测试[16]。将表面粗糙的无渗透率的假岩心装入岩心夹持器中,用定内压变外压的方式进行了测试。结果表明,微间隙贡献的渗透率值最高可达0.17 mD,微间隙对渗透率的贡献在围压低于15 MPa时非常显著。
罗瑞兰[19 ]认为,在实验过程中,可能由于岩样表面不光洁或形状不规整,岩样与封套之间存在一定微间隙,在围压较低状态下(小于3 MPa),如果流体驱替压力较高(大于2 MPa),则可能出现流体沿微间隙窜流的现象,从而使实验结果产生误差。
1.3 不同渗透率岩心测试稳定时间差异大
低渗透岩心测试时,渗流流量太小,仪器难以精确计量,很容易把微弱的流量近似为零。低渗透岩心建立稳态流动需要很长时间,达到稳态流动需要几天甚至几周。在岩心注入端施以压力变化之后,根据波的传播理论,压力由岩心注入端传播到出口端所需的时间为
t=μφCtx2/2K
(1)
式中:t为传播时间,ks;μ为流体黏度,mPa·s;φ为岩石的孔隙度,%;Ct为地层的总压缩系数,MPa-1;x为压力在直线地层中传播的距离,m;K为岩石渗透率,mD。
由式(1)可以看出,压力传播时间与渗透率成反比。岩石渗透率变化范围大,不同地层的渗透率差别可达数千甚至上万倍。目前,实验室判断岩心测试是否稳定的条件为,在一定时间间隔(15 min 或30 min)内,压力变化小于某个设定值。显然,这种无差别的判断标准是不科学的。许多低渗透岩心的测试过程中,表面上看似稳定,实际上并没有真正达到稳定,由此测得的渗透率将存在较大的误差。
应力敏感的研究手段以实验为主,研究过程大多为:实验测试—结果分析—微观机理分析—得出结论。由于所选岩心物理力学性质的差异,加之岩心的表皮效应、实验装置的承压能力、测试方法及系统误差等因素的影响,不同学者采用不同设备得到的结果差异甚大,实验研究存在较大的局限性,实验结果难以反映岩石渗透率的真实特性。
2 有效应力的误用放大了应力敏感程度
岩石是一种典型的多孔介质,储层岩石受到外部应力和内部应力(孔隙流体压力)的共同作用。由于岩石受到复杂应力作用而无法进行工程计算,研究岩石的力学行为必须采用有效应力。所谓有效应力,是一种等效应力,它作用于多孔介质的力学行为与内、外应力同时作用于多孔介质所产生的力学行为完全相同。目前使用的有效应力理论主要有Terzaghi有效应力、Biot有效应力和双重有效应力理论。
Terzaghi有效应力公式为:
(2)

针对Terzaghi 有效应力在工程应用中的不适应性,M.A.Biot于1941年提出了修正式:
(3)
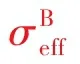
由于α值难以确定,许多学者为了简化研究,取α=1 。
李传亮于1999年提出了双重有效应力理论,认为岩石有2个有效应力:本体有效应力和结构有效应力。在分析岩石的弹性变形时须使用本体有效应力,其计算公式为:
(4)
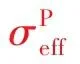
李传亮对3种有效应力进行了深刻对比、分析和论证,指出了Terzaghi有效应力和Biot有效应力的缺陷与适用条件。在分析岩石(尤其是致密岩石)的力学行为时,若采用Terzaghi有效应力或Biot有效应力,可能得到错误的结果。双重有效应力理论对Terzaghi有效应力和Biot有效应力进行了改进,其工程应用上适应性更强。
在进行应力敏感分析时,选用不同的有效应力得到的结果大不相同。根据表1,若采用Terzaghi有效应力,孔隙流体压力下降18 .0 MPa,有效应力从2.0 MPa升至20 .0 MPa,渗透率由0.049 mD降至0.016 mD;若采用本体有效应力,假设φ=10%,孔隙流体压力下降18.0 MPa,有效应力从2.0 MPa升至3.8 MPa,渗透率由0.049 mD下降至0.038 mD。以文献[5]为例,在进行实验数据分析时,采用Terzaghi有效应力,得出“低渗透储层存在强应力敏感”的结论。显然,有效应力的误用放大了储层应力敏感程度。
3 应力敏感评价理论计算公式
应力敏感问题属于岩石的力学问题。为了克服实验测试的局限,解决生产实践不能对“孔隙流体压力下降导致储层渗透率降低”进行单一因素定量评价的难题,应该从岩石力学角度进行研究,从理论上推导得出定量计算公式,揭示储层应力敏感的内在规律。
3.1 公式的推导过程
油气藏开发过程中,孔隙流体压力下降幅度远低于岩石的屈服应力,岩石一般不会发生塑性变形。在以下分析中,做出2点假设:储层岩石为各向同性体;孔隙流体压力下降之后,岩石只产生弹性变形,不产生塑性变形。
油气采出之前,储层岩石所受外应力为最大水平主应力(σH)、最小水平主应力(σh)和垂向应力(σz),内应力为孔隙流体压力(pp)(图2)。
根据式(4),储层岩石有效应力为:
(5)
式中:σeffH、σeffh、σeffz分别为岩石在最大、最小水平主应力和垂向应力方向上的有效应力,MPa。
根据式(5),储层岩石的体积应力(有效应力,MPa)为:
σeff=σeffH+σeffh+σeffz=σH+σh+σz-3φpp
(6)
油气采出之后,孔隙流体压力降低Δpp,外应力(σH、σh、σz)保持不变,如图2b所示。孔隙流体压力下降,岩石骨架所受应力增大,岩石压缩。由于岩石总体积与孔隙体积同步压缩,因此,孔隙度不变。
根据式(6),岩石的体积应力变化量为:
Δσeff=3φΔpp
(7)
根据弹性力学理论,岩石的总应变为:
(8)
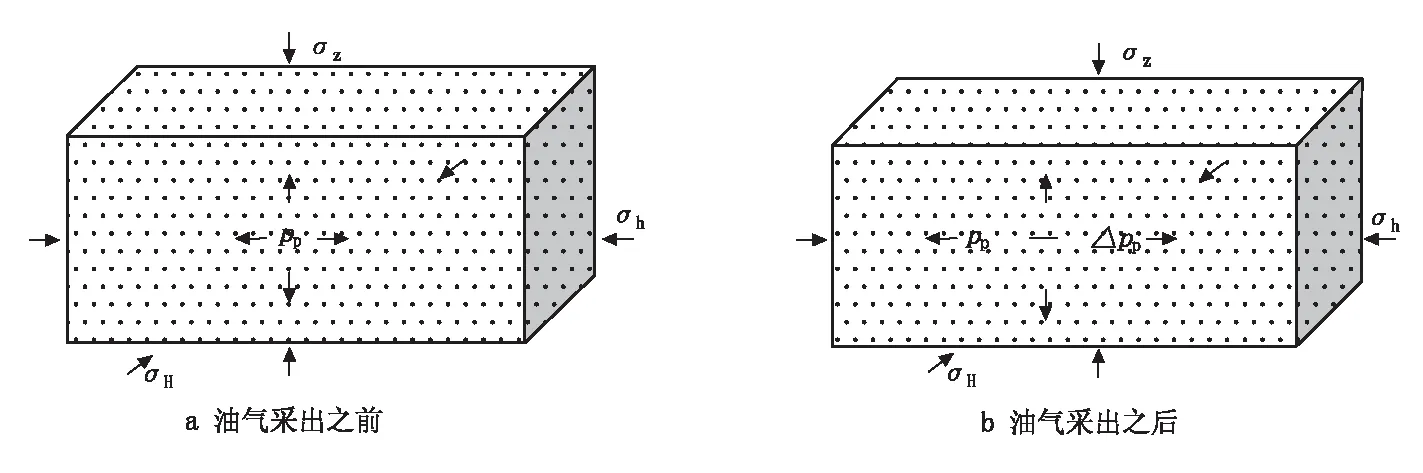
图2 油气采出前后储层岩石受力状态
(9)
式中:Mv为岩石的体积模量,MPa;ν为岩石的泊松比;E为岩石的杨氏模量,MPa。
由式(7)—(9)得:
(10)
式(10)即为孔隙流体压力变化量与岩石应变之间的关系式。
低渗透储层裂缝不发育,储集空间以孔隙为主,属于孔隙型储层。多孔介质是由大量的孔隙(毛管)组成的,渗流过程是通过大量管子中的流动(管流)来实现的。因此,孔隙型储层可以用图3中的毛管束模型来模拟图4中的多孔介质,用地层中一束管子的管流来模拟实际岩石中的渗流。
图3 多根管子(管子束)流动
图4 多孔介质渗流
油气采出前、后,设毛管体积分别为Vp0(10-12m3)、Vp1(10-12m3);毛管平均半径分别为r0(μm)、r1(μm);毛管长度为Lp(m),保持不变;毛管迂曲度分别为τ0、τ1;毛管数量为n。则有:
(11)
(12)
Vp1=(1-ε)Vp0
(13)
由式(11)—(13)可得:
(14)
油气采出前后,岩石的长度分别为L0(m)、L1(m)。由式(5)可知,在3个主应力方向上的应力变化相等,则3个主应力方向上的应变也相等。岩石的长度变化满足:
(15)
毛管长度、迂曲度和岩石长度之间的关系式为:
Lp=τ0L0=τ1L1
(16)
由式(15)和(16)可得:
(17)
根据Kozeny-Carman方程,油气采出前渗透率(K0,mD),油气采出后渗透率(K1,mD)分别为:
(18)
(19)
由式(18)、(19)可得:
(20)
将式(14)、(17)代入式(20)中可得:
(21)
将式(10)代入式(21)中可得:
(22)
孔隙流体压力降低Δpp之后,储层岩石渗透率损失百分数(SIp)为:
(23)
由式(10)和式(22)可知,油气采出之后,孔隙流体压力下降,岩石应力状态改变,其产生的应变由岩石的力学性质和孔隙度决定;储层岩石的应力敏感与岩石的杨氏模量、泊松比、孔隙度以及孔隙流体压降有关,初始渗透率和岩石应力敏感并无直接关系。孔隙流体压降一定时,孔隙度越大、杨氏模量越小,岩石的应变量越大、渗透率损失越大;反之,孔隙度越小、杨氏模量越大,岩石的应变量越小、渗透率损失越小。
3.2 计算讨论
根据式(10)、(22)、(23),取常规储层岩石物理力学参数φ=18%、ν=0.29、E=7×103MPa;低渗透储层岩石物理力学参数φ=8%、ν=0.25、E=30×103MPa,对储层岩石的应变、渗透率损失百分数进行了计算,结果如图5、6所示。
由图5、6可知,储层岩石物理力学参数一定时,岩石的应变与孔隙流体压降呈线性关系;岩石的渗透率损失与孔隙流体压降近似呈线性关系;由于孔隙流体压降在数值上远小于岩石的杨氏模量,岩石的应变极其微弱,孔隙体积的压缩幅度极小,渗透率损失很小。计算结果表明,低渗透储层不存在强应力敏感。
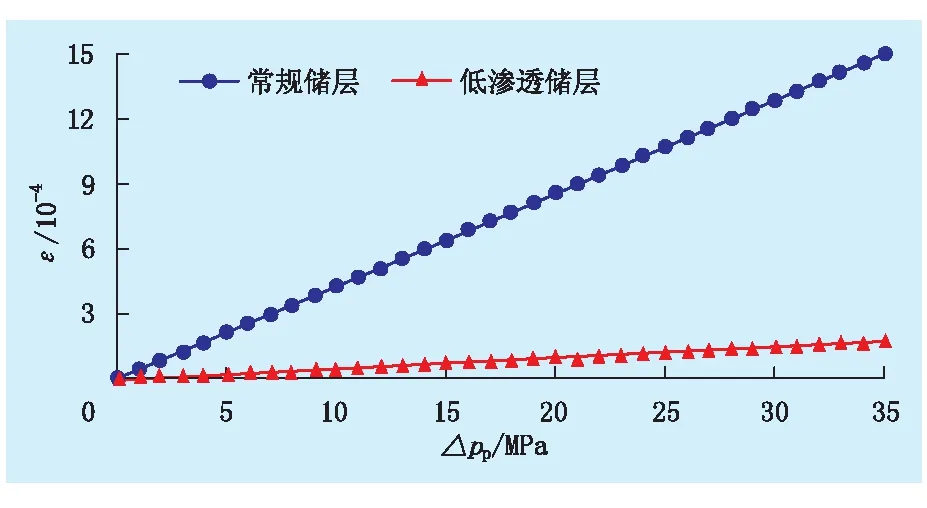
图5 储层岩石的应变曲线
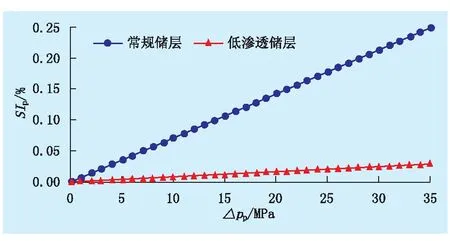
图6 储层岩石的应力敏感曲线
4 结 论
(1) 应力敏感实验由于多种因素的影响存在较大的局限性,实验结果难以反映岩石渗透率的真实特性。
(2) 在进行应力敏感评价时,选用不同的有效应力得到的结果差异较大,错误使用Terzaghi有效应力,放大了储层应力敏感程度。
(3) 储层的应力敏感与岩石的杨氏模量、泊松比、孔隙度以及孔隙流体的压降有关,与岩石初始渗透率无关。孔隙流体压力下降导致的岩石应变极其微弱,孔隙体积的压缩幅度极小,渗透率损失很小。
(4) 低渗透储层不存在强应力敏感。
