致密砂岩储层压裂有限离散元分析
2019-03-15薄江伟罗明良温庆志房堃徐胜强
薄江伟,罗明良,温庆志,房堃,徐胜强
(1.中国石油大学(华东),山东 青岛 266580;2.北京大学,北京 100871;3.北京大学工程科学与新兴技术高精尖创新中心,北京 100871;4.中国石化石油工程技术研究院,北京 100101)
0 引 言
低渗透油气藏在全球范围内分布广泛且储量丰富,但由于其岩性致密、低孔低渗等特点,油气产能较低,需实施增产措施。水力压裂技术可在储层中形成有效的油气运移通道,是开发低渗透致密油气藏的重要手段,水力裂缝的扩展路径、裂缝规格和数量是影响储层泄油面积和产能的主要因素[1-5]。为了使用适当的非线性本构关系对储层进行描述,并解决传统有限元方法中裂缝不能交叉的问题,利用有限离散元方法建立了二维流-固耦合水力压裂计算模型,借助有效应力分析法和损伤起始及演化准则,对岩体的变形、破坏和裂纹的萌生、扩展进行模拟[6-17],研究水平地应力差和压裂液黏度对水力裂缝发育和裂缝规格的影响,并优选出适用于特定储层的最佳工况条件。
1 有限离散元数值模型建立
1.1 有限离散元法
有限离散元法(FDEM)将有限元方法和离散元方法相结合,在具有孔隙压力自由度的四边形实体单元(蓝色单元集)的公共边插入零厚度黏结(cohesive)单元,共同组成复合单元(绿色单元集)。cohesive单元(黑色线段)和渗流节点(黑色圆点)构成了贯通模型的流体流动网络(图1)。cohesive单元的黏结作用会使其与相邻单元的变形一致,当cohesive单元未断裂时,可表示连续体的变形;当cohesive单元断裂时,可模拟岩石的破裂和裂纹的扩展。

图1 四边形实体单元和黏结单元的连接与液体在黏结单元中的流动示意图
储层进行水力压裂,当不可压缩流体通过黏结单元时,裂隙随着施加在其表面的载荷变化发生张开或闭合,缝中流体的流速和压力也会受一定的影响。与此同时,由于黏结单元和具有孔隙压力自由度的四边形实体单元之间存在压力差,缝中流体也会向壁面两侧的四边形实体单元中滤失。
缝中流体在黏结单元中的切向流动可以表示为:
qd=-KtΔp
(1)
(2)
缝中流体的法向滤失可以表示为[18]:
qt=-Ct(pi-pt)
(3)
qb=-Cb(pi-pb)
(4)
式中:q为流体切向流动速率,m/s;Δp为黏结单元的压力梯度,Pa/s;d为裂缝张开宽度,m;Kt为切向渗透率,m3/(Pa·s);μ为流体黏度,Pa·s;qt、qb分别为流体滤失到壁面两侧的速率,m/s;pi为黏结单元中的流压,Pa;pt、pb分别为壁面两侧单元的孔隙压力,Pa;Ct、Cb分别为滤失过程中壁面两侧的单元系数,m/(Pa·s)。
1.2 数值模型
基于有效应力分析法[19]和FDEM法共同建立流-固耦合计算模型,综合考虑骨架变形、孔隙流体压力消散的耦合作用。在水力压裂过程中,裂缝的起裂和延伸由张性破坏和剪切破坏共同作用,模型采用二次名义应力准则作为损伤起始准则,给定应力分别和3个方向的应力峰值比值的平方和为f,当f值为1时,将会发生损伤破坏[20]。一旦发生损伤破坏,会根据断裂能准则进行演化,该模型将BK能量准则作为损伤演化准则[21]。
二次名义应力准则:
(5)
BK损伤演化准则:
(6)
Gs+Gt=GS
(7)
Gn+GS=GT
(8)
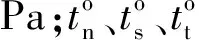
基于上述分析,根据四川盆地某致密砂岩油气藏地质资料,利用FDEM法建立了400 m×400 m的二维流-固耦合计算模型,忽略天然裂缝的影响。该地区储层深度为4 985 m,岩石最大水平主应力为67.7 MPa,最小主应力为61.2 MPa,垂向应力为73.3 MPa,泊松比为0.172,弹性模量为26.4 GPa,平均孔隙度为3.65%,平均渗透率为4 mD。通过不断向井筒中注入不可压缩牛顿流体,模拟KGD型裂缝[22]在满足德鲁克-普拉格准则[19]的本构模型中起裂和扩展。
2 数值模型验证
利用真三轴压裂模拟实验系统对该地区岩石进行水力压裂模拟实验,同时,采用FDEM法对该实验模型进行数值模拟。
图1为物理模拟和数值模拟结果(黑色圆点为注入点位置)。由图1可知,水力裂缝大致沿水平最大主应力方向扩展,数值计算结果与物理模拟实验结果吻合良好。

图2 物模实验与数值模拟结果对比
3 数值模型计算分析
3.1 水平地应力差对裂缝规格及数量的影响
压裂液黏度为80 mPa·s时,模拟求解水平地应力差分别为0、2、4、6、8 MPa时的裂缝起裂和延伸情况,然后通过编程获取不同地应力差时的裂缝长度(表1)和面积(裂缝面积为每段水力裂缝的长度与宽度乘积的累加和)随时间变化曲线(图3)。由表1、图3可知:在整个压裂过程中,形成的裂缝长度约为103~165 m,平均裂缝宽度约为5.25~8.66 mm(表1),裂缝面积约为0.78~0.97 m2;当岩石破裂压力大于扩展压力时,裂缝破裂后,随着裂缝的扩展,裂缝面积会越来越大,缝内净压力会逐渐减小,裂缝长度的增加速率会逐渐下降;当岩石破裂压力小于扩展压力时,裂缝不会扩展,在没有砂堵等情况发生时,需要重新憋压,升高至破裂压力才能使裂缝重新破裂,故裂缝会一段一段地扩展;水平地应力差越小,第1破裂阶段的缝长越长,进入第2破裂阶段的时间越快;随着水平地应力差的增大,最终缝长会先增大后减小,且地应力差为2~4 MPa时,裂缝最长,约为160 m;随着水平地应力差的增大,裂缝面积先增大后减小,平均缝宽则会一直增大。在低渗透致密储层中,增加裂缝长度比增加裂缝导流能力对增产更为有利。综上所述,在水平地应力差为2~4 MPa的工况下进行压裂施工时,形成的裂缝较长,更符合低渗透储层的改造要求。

表1 不同水平应力差的平均水力裂缝宽度
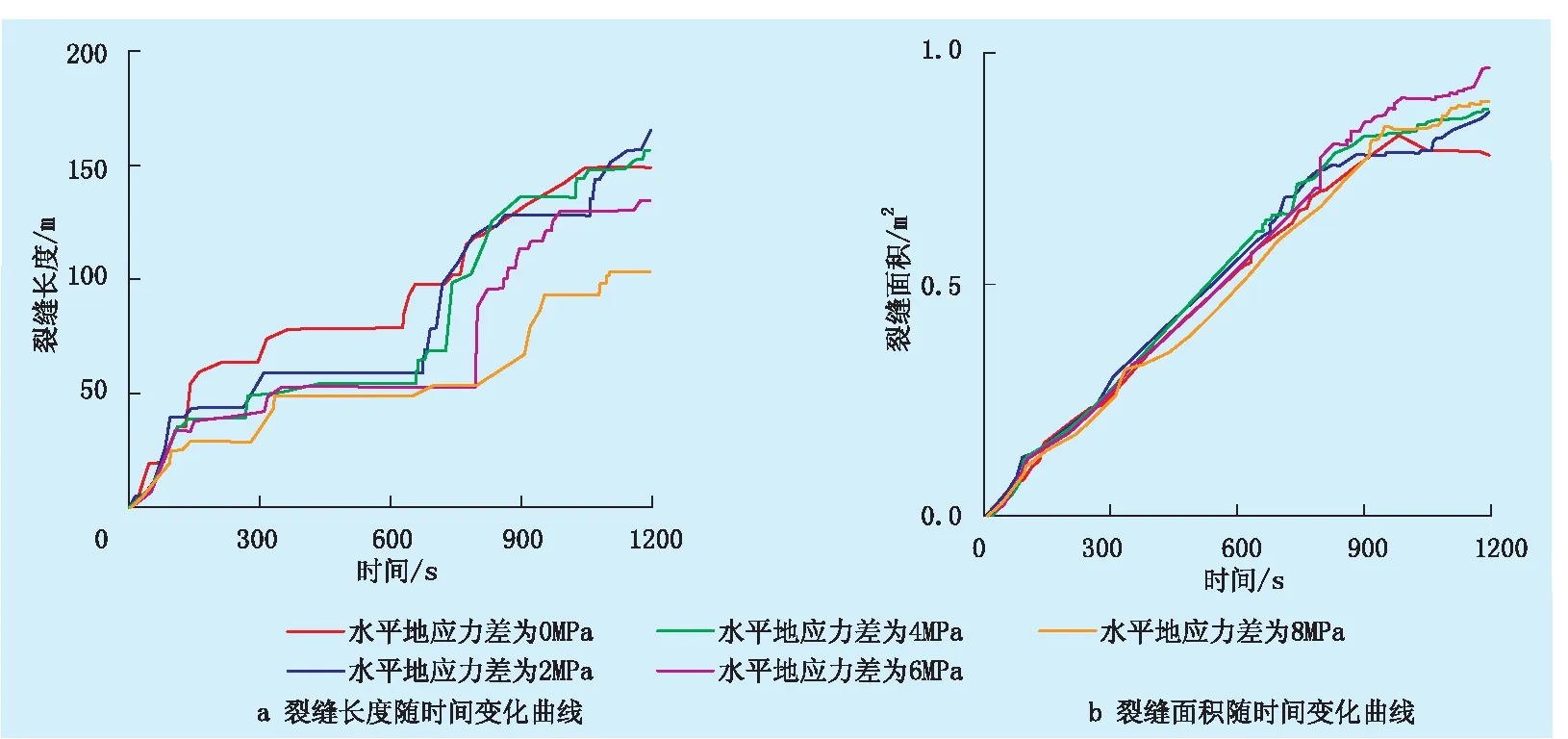
图3 不同水平地应力差时的裂缝长度和面积随时间变化曲线
3.2 压裂液黏度对裂缝规格及数量的影响
水平地应力差为4 MPa时,模拟求解压裂液黏度分别为40、60、80、100、120 mPa·s时的裂缝起裂和延伸情况(表2,图4、5)。由图4可知,模型中不同位置处的外载荷不同,当水力裂缝扩展到不同位置时,缝宽也会发生变化。结合表2可知,使用
高黏度压裂液时会形成较宽的裂缝,黏度低时会形成细长的水力缝,且黏度为60 mPa·s时会有缝网结构出现。

表2 不同压裂液黏度的平均水力裂缝宽度

图4 不同黏度下前端裂缝云图
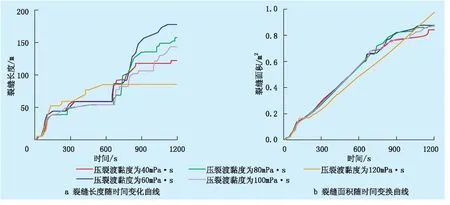
图5 不同压裂液黏度时的裂缝长度和面积随时间变化曲线
由表2和图5可知,在整个压裂过程中,形成的裂缝长度约为85~178 m,平均裂缝宽度约为4.95~11.35 mm,裂缝面积约为0.80~1.00 m2;当黏度较低时,压裂液易滤失到地层中,导致缝内有效流体体积变小,但压裂液在缝内流动越快,压裂液充满裂缝的时间越短,进行下一阶段的岩石破裂进程越快。反之,压裂液黏度越高,越不容易滤失到地层中,在缝内流动性越差,随着裂缝的扩展,缝内压降梯度也会随着压裂液黏度的增加而减小;与此同时,随压裂液黏度的增大,最终裂缝长度会先增大后减小,且黏度为60 mPa·s时,裂缝总长度最长,为177 m;随压裂液黏度的增大,裂缝面积大致为一直增大的趋势,平均缝宽会先减小再增大。结合以上分析可知,当压裂液黏度为60 mPa·s时,水力裂缝最长,更容易形成复杂的缝网结构,增大低渗透油气藏的泄油面积。
4 实例应用
对四川盆地某致密砂岩油气藏A井进行压裂施工,按照压裂施工设计,使用交联比为100.0∶0.4,黏度为60 mPa·s的压裂液,以4 m3/min的排量泵入40~70目陶粒支撑剂,施工时间为35 min,油压最高为62.4 MPa,经微地震分析,裂缝总长度为342.0 m,压裂后日产液量为25.7 t/d,日产油为21.4 t/d。利用有限离散元数值模型根据该地区储层资料和工况条件进行模拟计算,裂缝总长度为356.7 m,表明数值计算的结果与微地震检测结果具有较好的一致性。
5 结 论
(1) 有限离散元数值模型可以较为真实地模拟地下岩石的变形、破坏和裂纹的萌生、扩展,通过Python语言编写程序,可对计算模型中水力裂缝的几何数据进行提取,并经过真三轴水力压裂实验证实其适用性,该方法有助于对不同工况下的压裂施工进行研究。
(2) 在致密油藏地质条件的基础上,水平地应力差在0~8 MPa范围内时,水力裂缝长度会随着水平地应力差的增大呈现先增大后减小的趋势,平均裂缝宽度会随着水平地应力差的增大而增大。压裂液黏度为40~120 mPa·s时,水力裂缝长度会随着黏度的增大先增大后减小,平均裂缝宽度则会呈现先减小后增大的趋势。
(3) 现场实践结果表明,有限离散元数值模型计算结果与微地震监测结果具有良好的一致性。有限离散元方法有助于压裂时机选择、压裂前评估、压裂后产能计算和经济效果评价,对致密油气藏开发具有重要意义。
