考虑基质收缩效应的煤层气藏产能评价

2019-03-15陈丽群

特种油气藏 2019年1期

李陈，赵刚，陈丽群

(1.北京大学，北京 100871； 2.中联煤层气有限责任公司，北京 100016；3.中国石油塔里木油田分公司，新疆库尔勒 841000)

0 引言

近年来，随着对煤层气藏开发研究越来越多，对煤层气的认识也越来越深[1-3]。由于煤层气藏脆性较大并存在吸附气，相比于其他类型气藏，煤层中的一些地质参数对开发生产过程中的压力变化更加敏感[4]。一方面，由于煤层基质的脆性较大以及裂隙的存在，在生产过程中，由于生产层压力的降低，上覆岩层将会压缩基质；另一方面，随着生产的进行，吸附气将通过解吸附作用从基质中解析出来，会导致基质周围的压力平衡被打破，基质受到的压力增加，基质被压缩。以上2种物理现象在渗流规律研究中表现为：煤层气的天然裂缝系统的孔隙度和渗透率随着压力变化，而在开采过程中压力随着时间变化，最终表现为开发过程中天然裂缝的孔隙度和渗透率随时间而变化，孔隙度和渗透率不再为一个常数，而是压力的函数[5-8]。目前，考虑煤层气基质收缩效应的解析解研究相对较少，考虑基质收缩效应的产能评价模型则更少。并且，考虑基质收缩的巨大计算量给产能评价模型软件化带来了阻碍[9-11]。针对上述问题，提出了新的拟时间函数，能够快速准确地计算考虑基质收缩效应的解析解。

1 物理模型

气藏中心一口压裂直井，地层边界为无限大边界、封闭边界或者恒压边界；水力裂缝为有限导流裂缝；生产条件为定压生产或者定产生产；整个气藏恒温、均质；气体的扩散发生在基质系统且为稳态扩散，渗流发生在天然裂缝系统和水力裂缝；考虑基质的收缩效应。

2 数学模型

2.1 天然裂缝流动数学模型

物质平衡方程：

(1)

式中：r为气藏模型径向半径，m；p为地层压力，MPa；μ为气体黏度，mPa·s；Z为气体偏差因子；φ为气藏孔隙度；cg为气体压缩系数，MPa-1；K为气藏渗透率，D；t为时间，d；psc为标准压力，MPa；T为气藏的温度，K；Tsc为标准温度，K；V为气体的浓度，m3/m3。

在处理基质扩散的过程中，采用拟稳态和非稳态扩散得到的物质平衡方程，右边是带有压力项的函数，目前的处理方法是令其约等于常数，这样通常会带来误差。另外，在考虑基质收缩的历史拟合中，每变一次压力或者产量会重新求解物质平衡方程，会使时间叠加原理带来巨大的计算量，用目前普通计算机无法解决，使得在软件化过程中不能考虑基质收缩效应。文中讨论的基质扩散模型可以有效地规避这一问题，在计算过程中不必假设压力常数，而且可以降低计算量，提高计算速度，在产能评价软件中可考虑基质收缩效应。

稳态扩散的物质平衡方程[12]：

(2)

(3)

式中：cd为吸附压缩系数，MPa-1；ψ为Hussainy拟压力[13]；pb为拟压力积分参考压力，MPa。

引入拟时间函数：

(4)

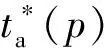
(5)

式中：VL为朗格缪尔体积，m3/t；pL为朗格缪尔压力，MPa。

该拟时间函数能够考虑渗透率及孔隙度对时间的变化，可以结合时间叠加原理使用。只需把孔渗随时间变化的关系式输入即可，而对于煤层的孔渗随时间变化关系已有诸多研究[14-17]。把拟时间函数带入式(2)中：

(6)

通过对扩散状态的合理设定以及拟时间函数的引入，能够完全地把煤层气藏中物质平衡方程的右边转化为常数。无因次化之后，可以根据边界条件和初始条件，得到式(6)的解为：

(7)

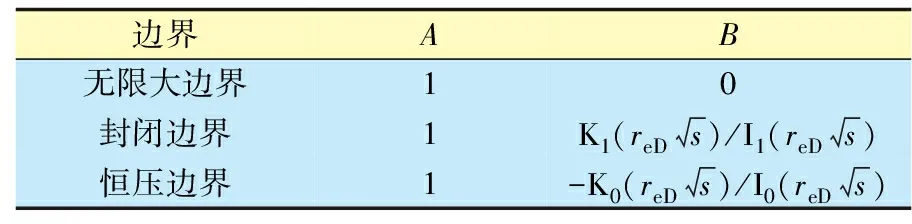
表1 不同边界条件下A和B的值

注：reD为无因次气藏半径；K1、I1为一阶贝塞尔函数。

2.2 水力裂缝流动数学模型

忽略裂缝中流体的压缩性，有限导流裂缝中的流动方程为[18-20]：

(8)

在理论解析解求解过程中，需要假设内边界条件为定值来得到解析解的特解，但在实际生产过程中，由于生产条件的影响，产量和压力一般是变化的，需要借助Duhamel褶积来对变化的产量或压力进行叠加，进而可以得到变产量和变压力下的理论解析解，实现理论解析解和实际生产数据的拟合，在拟合的基础上最终实现气井的产能评价和产量预测。

3 实例分析

3.1 压力影响分析

实际井的生产数据来自FEKETE软件中的例子，基本参数如表2。基质收缩模型采用Seidle and Huitt模型[6]，其表达式为：

(9)

(10)

式中：φi为原始状态下的渗透率，D；dCm为基质收缩系数，t/m3，pi为原始状态下的地层压力，MPa；Ki为原始状态下的地层渗透率，D；n为孔渗关系指数。

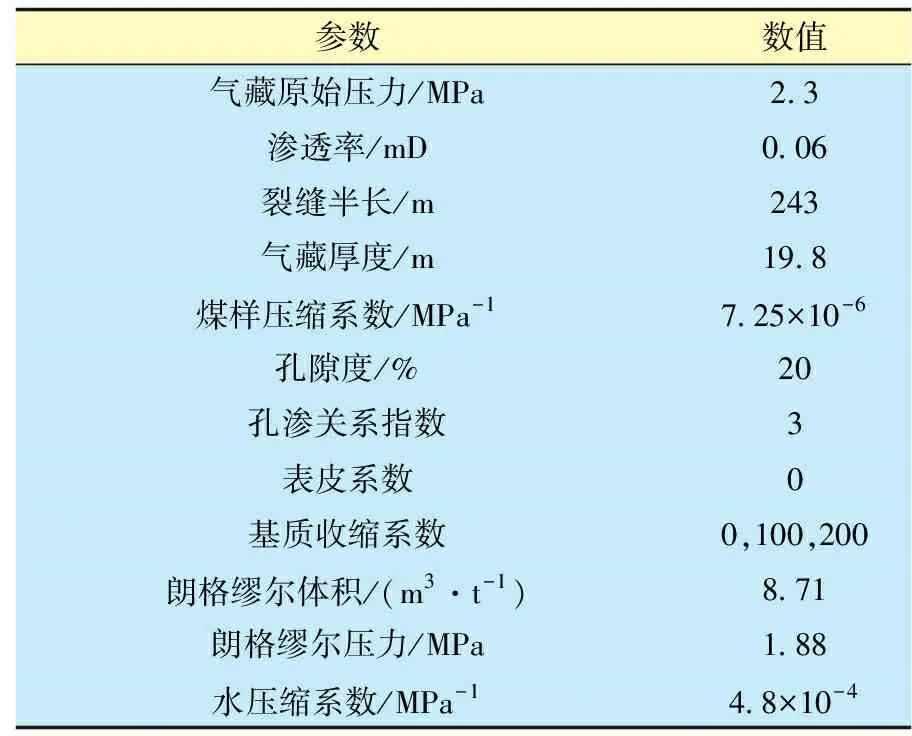
表2 基质收缩效应对比基础参数

基质收缩是由基质的解吸现象及基质受到压缩所导致的，在前期吸附气体解吸不明显，基质收缩对无因次井底压力影响不大，随着开采的进行，基质收缩影响越来越明显。对于Seidle and Huitt模型而言，随着压力的降低，基质收缩会使得渗透率增加，从而使得地层的渗流条件变好，在定流量的前提下，地层中的压降会降低，地层能量的利用率提高。

3.2 模型实际应用分析

以中国沁水盆地樊庄区块压裂直井为例。该区块位于沁水盆地南部晋城马蹄形斜坡带，煤层厚度较大，可采煤层包括3号、9号和15号，中山西组3号煤层为目前开发的主要煤层，埋深为400～700 m，总体上东深西浅，一般厚度为5～6 m，总体上东厚西薄，分布稳定，煤层结构简单，底部常发育0.7 m左右的构造煤[9]。

选取樊庄区块6口具有基质收缩效应的单井为例，由岩心应力测试数据可知，这些井及其附近煤层具有较强的基质收缩特性，故采用考虑基质收缩特性的煤层气藏解析解模型来对生产数据进行拟合，基质收缩模型采用适用范围较广的常指数渗透率模型[5]。FZ-1井基础数据见表3，根据时间叠加原理，采用文中得到的产能方程对单井产气量、井底流压以及累计产气量等历史生产数据进行拟合，通过历史拟合对比，解析解的拟合参数与目前单井认识基本相同(表4)。

表3 FZ-1井基础数据

通过理论模型与现场6口生产井对比，考虑基质收缩效应能够得到准确的产能评价结果，与现场认识误差均在10%以内(表4)，其中，地层系数平均误差为4.10%，渗透率平均误差为4.41%，孔隙度平均误差为7.84%，基质收缩系数平均误差为4.30%，裂缝半长平均误差为6.83%。单井生产数据拟合结果显示，考虑基质收缩效应能够有效地提高拟合结果，降低拟合误差(表5)，其中，压力平均拟合误差降低了45.80%，产量平均拟合误差降低了45.10%，累计产气量平均拟合误差降低了89.80%。在历史拟合的基础上，可以设定井底流压，对单井未来的产量进行预测。