中学生数学演绎推理形式的校际表现研究＊

郝连明

一、问题提出

中学阶段是从形象思维过渡到抽象思维的关键时期，所以要尤为重视对学生推理能力，特别是演绎推理能力的培养。数学推理是数学教育中的重要内容，刚刚公布的高中数学课程标准的六个数学核心素养就包括逻辑推理，其中逻辑推理分为演绎推理和归纳推理。[1]这也表明数学是培养学生推理能力的重要载体。有关数学推理的研究有很多，早在20世纪我国学者在探讨数学三大能力时就开始了相关研究。根据他们对国内文献的梳理，逻辑推理的研究主要集中在内涵结构、教学、现状、教材、课程等几个主要方面。[2]在现状调查中，学者们普遍从小学、初中、高中三个阶段开展研究，了解学生在数学推理上的表现情况。一些研究表明，初中阶段的八年级是培养推理能力的重要时期，高二年级是高中阶段的重要时期。[3][4]有学者在具体结论分析中发现男生表现比女生更优异，[5]也有学者不支持这种观点，认为不存在明显的性别差异。[6]在学校类型的对比中，一些研究表明存在明显的地域差异，城市学校的学生表现明显好于农村学校的学生，但也有学者不支持这一结论。[7]在对主要结论的简要梳理中发现，学者们对数学推理开展了很多研究，但是没有形成统一的结论。究其原因，主要是实证研究中受多种因素的影响，而诸多变量中任何一个都可能导致结果的不一致。研究中学者们往往使用不同的测试工具，构建了不同的测试框架，采用了不同的统计技术和分析软件。另外，参与测试的学生群体也可能不同，优质学校学生会好于普通学校学生，样本的选择没有代表性也会影响测试的结果。同时，学者自身对推理的认识也会产生差异。数学推理素养、数学推理能力、演绎推理、数学证明等核心概念的不同认知，也会造成测试内容的不同。如果不控制更多的变量因素，一定会造成结果不一致。因此，在研究中需要更进一步地设计研究框架，尽可能地控制其他变量的干扰。基于现有的研究发现，仅关注学生在数学演绎推理上的校际差异表现较少，一些现状调查研究并没有报告不同水平学校之间的差异，而且较少有单独报告学生在数学演绎推理形式上的表现情况。因此，基于对数学演绎推理形式的认识，本研究将开展针对不同学校的测试研究。

二、构建测评框架

本研究主要是调查不同学校学生在数学演绎推理形式上的表现情况。因此，构建测评框架成为首要任务，只有构建了测评框架，才能进行工具开发、测试、数据分析等工作，进而根据数据分析结果得出结论。

很多关于数学演绎推理的测试和研究都基于形式逻辑学的分类进行，数学有自身独特的学科特点和发展路径。因此，数学演绎推理的研究要基于数学学科本身的角度进行分析。一些学者虽然从数学本身关注了推理的研究，但容易将数学证明等同于数学演绎推理，虽然二者表现形式一致，但却有差别，不能等同视之。例如，在英国一项有关数学证明的调查中发现，很多学生在构建证明时很少使用演绎推理。[8]因此，本研究将构建新的测试框架来考察演绎推理的形式表现。史宁中教授指出，论证依靠的是公理，推理依靠的是形式，[9]即推理过程实质是一个对形式规则应用的过程。

通过对文献的梳理发现，史宁中教授从数学学科本身角度详细说明了数学推理的几种不同类型。他认为数学推理是有逻辑的推理，其中的逻辑性是指推理过程满足传递性。通过基于数学知识的发展过程，认为数学推理存在两种类型，一是性质传递推理，二是关系传递推理。

基于这样的认识，在本研究中将数学推理形式分为三个类型：三段论、关系、运算。其中每一个维度又划分了多个子维度。具体测评框架如下：

三、研究设计

（一）研究对象

通过对已有研究的梳理发现，很多学者都指出初中阶段的八年级是最关键的时期。例如，德国在一项的测试研究中，发现八年级学生的推理能力提升最明显。[11]我国的初中阶段，八年级刚开始讲授证明，学生的初中学习也进入一个相对稳定的时期。因此，本研究选择了八年级学生进行测评，具体测试学生为刚刚升入九年级的学生，确保学习了完整的八年级知识。学生用的人教版教材，学生来自吉林省某地级市3所学校。根据整体抽样方法，3所学校代表不同层级教学水平，其中学校1最好，学校2居中，学校3较弱。

（二）研究工具

在测试工具开发中研究者与多位数学教育工作者进行了商讨，经过几轮修订最终形成了数学演绎推理形式测试问卷。由于本研究的目的是测试学生在演绎推理形式方面的表现情况，因此，在测试工具的开发中尽可能地控制了数学知识对测试结果的影响，工具中尽可能通过简单符号、语言来表述，规避数学知识带来的认识负荷。最后经过可靠性检测，问卷系数为0.727。虽然从信度的数值来看不高，但是在测试内容上已经能够达到测试的要求，具有较好的专家效度。测量学的数值指标只是更好地实现测试目的，但是测试的目的并不是为了构建好的测量学指标。经过最后的修订形成了数学演绎推理形式测试量表。实际测试中共发放问卷230份，回收230份。经过有效性筛选，剔除部分无效问卷后获得224份有效问卷，问卷结果采用SPSS20.0软件进行分析。

四、结果及分析

（一）关系推理结果表现分析

关系推理总体学校1学校2学校3 min 1 1.2 1 1.2 max 2 2 2 2 std 0.24 0.15 0.2 0.26 mean 1.82 1.92 1.9 1.72 p（男，女）0.98 0.43 0.23 0.62

从上表中可以看出，学生在关系推理上表现较好。总计5道测试题，满分为2分，学生的平均分达到1.82。其中有119名学生满分，占比53.1%。不同学校学生之间存在一定差异，其中学校1和学校2表现较好，学校3表现较弱。通过单因素方差分析发现，这种差异达到了统计学上的显著性，其中P（校1，校2）=0.50>0.01，而P（校1，校3）=0.00<0.01，P（校2，校3）=0.00<0.01。这表明在关系推理方面学校之间存在差异，低水平学校学生表现明显弱于高水平和中等水平学校学生，而高水平和中等水平学校学生之间不存在差异。从性别角度看，整体上男生和女生之间不存在显著性差异。进一步从学校层面看，不同学校都不存在性别差异，P值都大于0.05，从一个侧面得出男女生在关系推理方面掌握较好。

（二）三段论推理结果表现分析

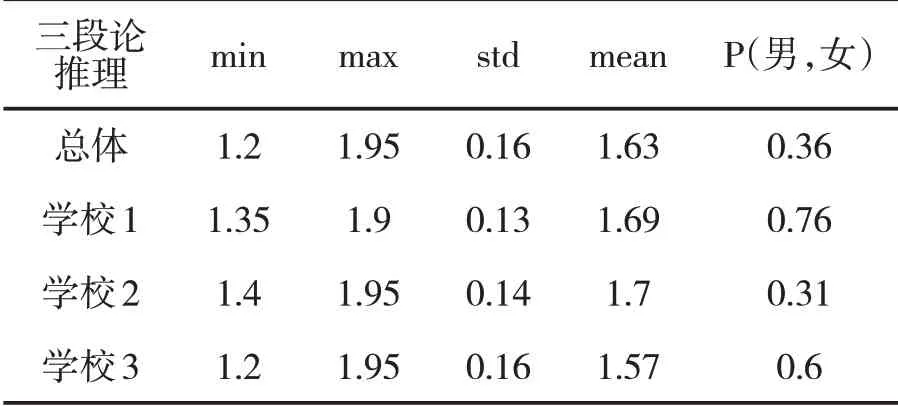
三段论推理总体学校1学校2学校3 min 1.2 1.35 1.4 1.2 max 1.95 1.9 1.95 1.95 std 0.16 0.13 0.14 0.16 mean 1.63 1.69 1.7 1.57 P（男，女）0.36 0.76 0.31 0.6

从上表看到，学生在满分为2分的三段论推理形式测试中平均分为1.63，最高分为1.95，全部参测的学生中没有能够得到满分。不同水平的学校表现与关系推理结果略有不同，中等水平的学校2表现最高，平均分达到1.70，学校3最弱，为1.57。通过方差分析发现，学校1和学校2之间的差异不具有显著性，P（校1，校2）>0.01，但是P（校1，校3）<0.01，P（校2，校3）<0.01，表明学校1和学校2的表现明显好于学校3，达到了显著性差异。从性别角度分析，三所不同学校中，男女生的表现不具有显著性差异，p值都大于0.05。在三段论推理的子维度中，不同性别学生在假言三段论、直言三段论、选言三段论上也不具有差异性。子维度表现上，学生在直言三段论和选言三段论表现较好，假言三段论表现一般，事实上几乎所有的数学定理都可以写成假言三段论的形式。例如，三角形内角和等于180°，可改写为“如果一个图形是三角形，那么这个三角形内角和等于180°。”可见，假言三段论对学生掌握数学知识，应用知识进行问题解决是至关重要的。在三段论题中，学生假言三段论题的平均分仅为1.61，试题为“如果成立，则成立。若成立，则一定成立。”对于这个命题进行判断。很多学生在该题做出了错误判断，认为一定成立。事实上根据这个前提只能严谨的说成立时，成立，而成立时是无法得出是否一定成立。如果加入数学知识进行思考，可以转化为“前提：平行四边形一组对边平行，结论：一组对边平行的四边形是平行四边形”。显然这个结论是错误的，该图形可能是梯形。由此可见，推理的规则隐藏在数学知识的推导中，教学中对各种知识的证明和推导可以有意识地渗透推理形式。

（三）数学运算结果表现分析

数学运算总体学校1学校2学校3 min 1.2 1.3 1.2 1.2 max 2 2 2 2 std 0.21 0.15 0.19 0.2 mean 1.71 1.82 1.8 1.61 P（男，女）0.52 0.54 0.6 0.16

从上表看出，学生在满分为2分的数学运算上平均分为1.71，学校之间的差异明显。学校1和学校2表现明显好于学校3。通过方差分析发现，P（校1，校2）>0.01，但是P（校1，校3）<0.01，P（校2，校3）<0.01，表明学校1和学校2之间不具有显著性差异，学校3与学校1和学校2之间都具有显著性差异。从性别角度看，男女生在数学运算上都不具有显著性差异，p值都大于0.05。数学运算推理不同于关系推理和三段论，以往的很多数学演绎推理研究中并没有加入数学运算。本研究基于数学推理角度出发，将数学运算纳入测试框架中。从结果看出学生在数学运算表现较好，其中四个子维度差异不大，运算公式上表现略好。

五、研究启示与不足

（一）关注不同学校之间的差异

通过对演绎推理形式不同维度测试结果的分析，3所不同学校学生之间的差异较为明显。其中高水平学校和中等学校学生没有表现出明显差异，但二者与低水平学校之间有明显差异，低水平学校学生的表现明显低于前者。虽然在很多学业成绩的测试，以及数学能力的测试中都反映出学校之间的差异，城市学校和优质学校的学生表现要好于其他学校，但并没有研究表明这种差异在演绎推理形式上也存在。本研究结果表明这种校际之间的差异在数学演绎推理形式层面也同样存在。因此，要关注不同学校层面学生数学演绎推理形式的差异情况，并针对这种情况开展更为深入的研究工作。

（二）关注不同形式推理的教学情况

通过本研究的测试结果发现，学生在关系推理上表现相对较好，但三段论和数学运算方面表现一般。三段论推理包含多个类型，其中假言三段论的形式较多，也不容易理解。前提和结论的肯定和否定容易使学生做出错误判断。由于几乎所有的数学定理都可以通过假言三段论的形式表现出来，所以三段论推理形式的学习显得尤为重要。因此，从推理的教学角度看，在课堂教学中对于不同推理形式要有一定的侧重，特别是三段论推理要重点强调，通过多种方式提高学生的应用能力。

（三）拓展性别差异的原因

本研究发现男生和女生并没有出现预期的差异，在所有测试中，一级维度和二级维度都没有呈现出显著性的性别差异。这种情况可能是由于测试样本量较小所导致，但是排除此种因素，推测出八年级学生的推理差异并不是由推理形式上的差异所导致，应该有更复杂的原因，如知识的掌握程度、家庭环境、个人兴趣等因素。因此，对性别差异的研究要更大范围的去讨论，不能仅仅停留在所研究的变量本身。

数学演绎推理是数学教育的重要研究领域，也是一种非常重要的数学能力，关注数学演绎推理的表现对开展教学研究具有重要的参考价值。虽然本研究存在一些不足，如测试样本数量较小，测试工具的信效度还有待进一步检验，但是一些测试结果有助于我们开展有关数学演绎推理形式的深入研究。