相关信道下基于功率分配的MIMO系统容量分析

0 引言

在整个通信系统中，信道容量要尽可能地达到或者接近理论最大值。因此，针对不同的环境、信道状态等，一般会对应有不同的功率分配算法来适应条件要求，以使得所用算法最合适，最终达到总容量最大化。无论在OFDM-MIMO系统[1],还是物理层多天线选择系统[2]，功率分配算法都发挥着重要的作用。文献[3]通过仿真和分析，得出注水算法在功率分配算法中最优。不过，在实际的无线环境中，衰落并不是独立的，而是存在着相关性，这个相关性会对整个系统的容量产生较大的影响。相关性越高，信噪比越小，整个系统的容量也随之越小。文献[4]研究了天线间距、角度扩展等参数对天线相关性，进而对信道容量的影响，但也仅限于发射天线上功率平均分配的情形。文献[5]讨论了天线相关性对信道容量的影响,但更侧重空时编码下的MIMO系统的译码性能。以上文献对MIMO系统容量的分析要么偏重功率分配，要么偏重相关性讨论，都还不够全面。本文综合了信道相关、功率分配两个方面，给出了四种情况下MIMO信道的容量，并通过仿真，分析了相关信道和非相关信道下不同功率分配对容量的影响，最后，引入了大规模MIMO系统中奇异值扩展的概念，通过其累积分布(cumulative distribution function,CDF)曲线，来分析MIMO信道的相关度，为基站灵活配置天线提供参考依据。

1 MIMO系统信道容量

假设一个MIMO系统，有Nt根发射天线和Nr根接收天线，将其表述为[6]

y=Hx+w。

(1)

其中：x表示的是发射端Nt根发射天线所发送的信号向量矩阵；y为接收端Nr根接收天线所接收的信号向量矩阵；H为Nr×Nt的矩阵，矩阵中的元素表示第i根发射天线发射的信号到达第j根接收天线之间的信道衰落系数，即信道增益；w为噪声向量，表示统计独立，均值为零，固定方差的加性高斯白噪声。如果在信道H未知的情况下，适合采用平均功率分配；如果信道H已知，则根据奇异值适合采用注水算法进行功率分配。

1.1 非相关信道下的容量

1)平均功率分配

通过对信道矩阵对角化，可得

H=UDVH。

(2)

U为一个Nr×Nr阶的酉矩阵，即U-1=UH。矩阵D内的对角线上的元素为信道矩阵H的奇异值，并且为一个Nr×Nt的对角矩阵。矩阵V为Nt×Nt阶的酉矩阵。将式(2)代入式(1)，可得

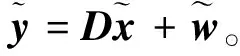
(3)

(4)

(5)

其中B为子信道带宽，P为MIMO系统发射端的总功率，σ2为信道噪声方差，γ=P/σ2表示信噪比，而γ/Nt表示平均功率分配下第i个子信道的信噪比。

2)注水功率分配

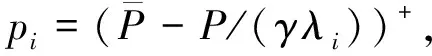
1.2 相关信道下的容量

为了探讨具有相关性的MIMO系统的信道容量，将信道矩阵H表达为[8-9]

H=R1/2HwT1/2。

(6)

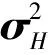
1)平均功率分配

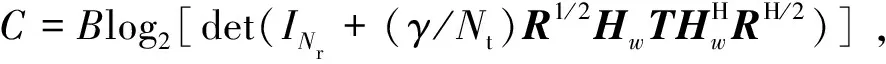
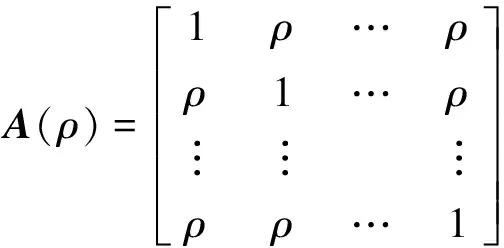
(7)

其中，ρ∈[0,1)为相关系数。令T=ANt(ρNt)，R=ANr(ρNr)，其中ρNt为发射端相关系数，ρNr为接收端相关系数。

2)注水功率分配

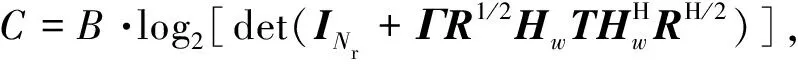
3)相关性度量

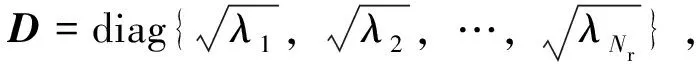
2 仿真及结果分析

基于MATLAB工具进行仿真实验。假设信道为瑞利衰落信道，信道噪声为零均值加性高斯白噪声，并且假设信道带宽、发射端的总功率保持不变，并对10 000次仿真结果进行平均。

图1为功率注水算法下相关信道与非相关信道的容量比较。可以看到，不具有相关性的信道容量会比具有相关性的大。因为相关性越大，对各个子信道来说，由于耦合效应，导致等效的信噪比就越小，总信道容量也就相应越小。同时看到，天线数的增加对信道容量的影响更大。

图2表示功率注水算法下相关信道与非相关信道的容量累积分布。可以看到，非相关信道的容量分布要优于相关信道的容量分布。同一概率时，非相关信道的容量比相关信道的容量大，且非相关信道的平均容量(曲线的中部描述)也比相关信道的平均容量大。而非相关信道的中断容量(曲线的底部描述)与相关信道的中断容量差别不大。

图3显示在信噪比为5 dB的情况下，随着相关系数的变化，不同功率分配下的信道容量影响趋势。可以看到，当天线数较少时，信道相关程度对信道容量的影响不大。但随着天线数的增加，信道相关程度对信道容量的损害越大。同时看到，功率注水算法能整体上改善信道容量，且在信道相关程度越大时效果表现得更为明显。

图4从信道的奇异值扩展,考察了信道的相关性与累积分布函数的关系。从图4中看出：当ρ越大，累积分布曲线越陡峭，说明相关性越低；另外，如果增加天线数目，累积分布曲线变就会得越差。由此可见，虽然天线数的增加能带来容量的增大(从图3亦能看出)，但也会影响天线之间的相关性。

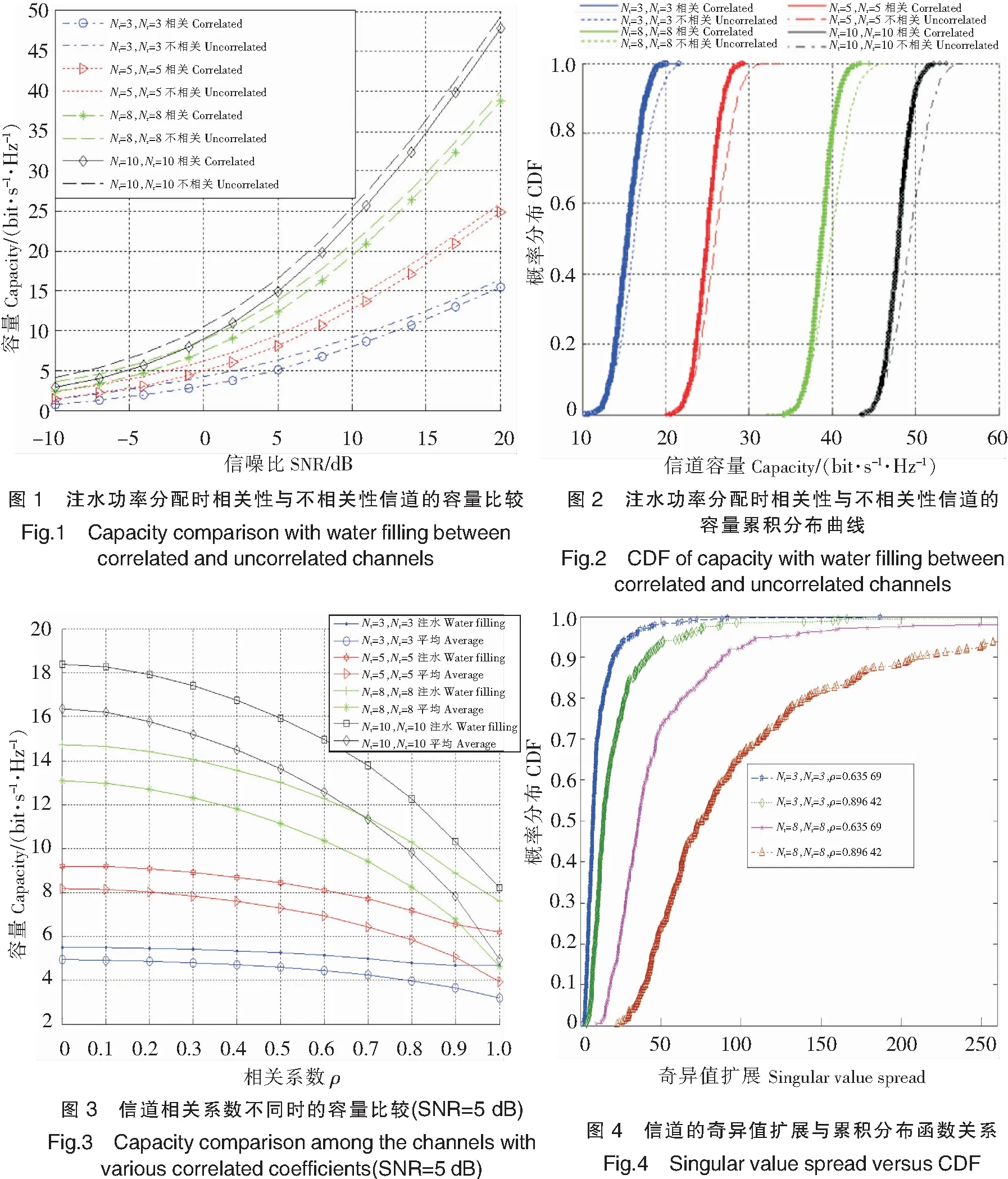
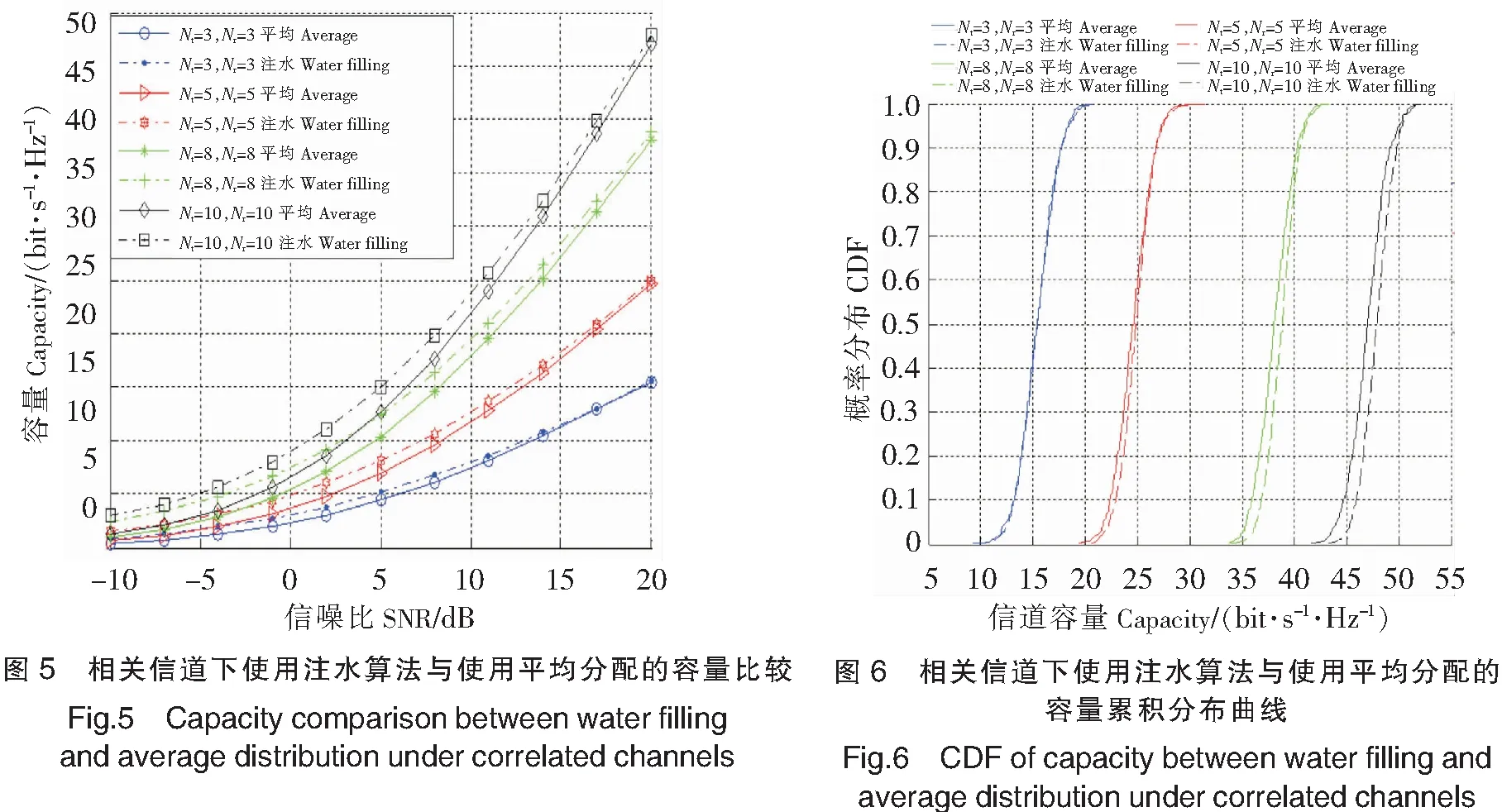
图5为相关信道下使用注水算法与使用平均分配的容量比较。可以看出，同样在具有相关性的MIMO系统，使用注水功率分配时得到的系统容量要比使用平均功率分配得到的系统容量高。而当信噪比越高时，这两种分配方式得到的系统容量就越接近。因为信噪比越高，信道状态越好。信噪比高到一定量时，可视为信道没有衰减，则每条子信道的信道信息一样好。此时，注水算法得到的分配方案就是平均分配。

图6表示相关信道下使用注水算法与使用平均分配的容量累积分布曲线。从图6可以看到：在天线数量较少时，注水功率分配的优势还体现不出来；而随着天线数量的增加，注水算法的优势越来越明显，其平均容量(曲线的中部描述)与平均分配时的差距越大；而相比平均容量，中断容量(曲线的底部描述)的差距表现得更为明显。