多属性采购拍卖中风险厌恶投标者投标策略研究

刘文雅

（1.四川外国语大学 国际商学院，重庆 400031；2.重庆大学 经济与工商管理学院，重庆 400030）

0 引言

拍卖（auction），长期以来都被人们当成一种有效的商品分配机制，而采购（procurement）可以将其视为一种逆向拍卖（或采购拍卖即投标者为卖方，采购者为买方）。采购和拍卖的一个明显区别在于：拍卖一般来说价格是决定获胜与否的唯一因素；采购获胜极少由价格唯一决定，实际采购过程中还需考虑商品的质量、售后服务及交货时间等因素，因此采购拍卖（或招投标）通常是多维的（multidimensional）。

多属性采购拍卖理论研究起源于20世纪90年代，Che[1]较早系统地研究多属性采购拍卖理论，是以美国国防部（DoD）的武器采购系统为研究对象，证明了在一定条件下第一得分（first-score）和第二得分（second-score）采购机制产生的预期效用是相同的。Branco[2]延伸了Che[1]的工作，假设投标者的成本函数中信息因子是随机且相关的。Asker和Cantillon（2008）[3]讨论了一个采购者和N个投标者的招投标模型，投标由价格p和M个非价格因素属性构成，证明了通过适当的方式将供货商的多维私有信息转变为一维信息不会影响采购拍卖均衡分析结果的充分条件。另一方面，对投标者来说，通过拍卖赢取投标会产生一定的风险，如果投标者不喜欢风险或对风险厌恶程度不同，则在不同的采购拍卖规则下的竞价策略也会不同[4-6]，从而导致采购者的预期收益会随采购规则发生变化。因此，有必要对带有风险厌恶投标者的多属性采购拍卖的投标策略进行研究。近期Liu等[7]在真实评分（naive scoring rule）的条件下讨论了带有风险厌恶投标者的多属性采购拍卖模型，所谓“真实评分”意味着投标者在知道采购者的真实偏好情况下进行投标，但实际采购拍卖中采购者一般不愿意公开自己的真实偏好，除非投标者和采购者出现共谋（Collusion）的现象。此外，在多属性采购拍卖中采购者往往不能准确评估投标者的投标。因此为了更客观地评估投标，有必要在充分反映采购者偏好的条件下，引入第三方评分（the third-party scoring）。

本文主要在文献[1，7]的基础上，通过引入Arrow-Pratt风险相关系统（Arrow-Pratt coefficient of risk-aversion）和第三方评分，研究带有风险厌恶投标者的多属性采购拍卖模型。在投标者知道自己效用函数的情况下，给出均衡投标策略的解析表达式，并分析了投标者的风险厌恶程度对投标策略的影响。

1 模型假设与理论分析

本文将给出关于多属性采购拍卖模型基本的定义和假设。首先假设市场中有某个采购者将购买某一种不可分割的物品(或服务)。该采购者将面对n个投标者，令N代表所有参与投标的投标者集合，则有：

那么i，j∈N将代表不同的投标者。本文假设需要采购的物品包含了一个二维属性:价格属性（用p表示）和质量属性（用q表示），其中q不仅表示采购物品的质量，本文假设它还包含了采购物品其他所有非货币属性。本文主要考虑两个多属性采购拍卖模型，即“第一评分拍卖”和“第二评分拍卖”，首先投标者通过密封投标的方式投一个包含(p，q)的标，采购者通过第三方评分的方式对所有投标进行评判。所谓“第一评分拍卖”是指得分最高的投标所产生的(p，q)为获胜投标；而“第二评分拍卖 "是指得分最高的投标者执行得分第二所产生的(p，q)。显然第一评分拍卖和第二评分拍卖分别类似于通常意义密封投标拍卖中的第一价格拍卖和第二价格拍卖。

为了更精确地说明q对于采购决策的影响，本文定义V(q)为质量属性q的量化函数V∶R→R。对于V(q)作下述假设:

假设1①假设1是为保证质量排序的单调性。：量化函数V(q)是一个单调递增的凹函数且V(0)=0。

本文将获胜投标者i从合同(q，p)中获得的效用定义为:

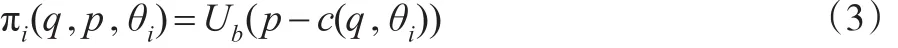
这里Ub是投标者的效用函数，c(q，θi)是投标者i的成本函数。本文假设c(q，θi)关于质量q和成本参数θi是递增的，而效用函数Ub也是一个单调递增的凹函数且V(0)=0。

本文假设投标者选择参与投标时不需要额外支付进场费(entry cost)。投标前每个投标者i都知道自己的成本参数θi，采购者只知道成本参数的分布函数。本文假设投标者的成本参数θi在上独立且服从同一分布函数F(θ),其中且F(θ)存在连续可微的概率密度函数f(θ)。由于本文假设投标者之间是完全对称的(complete symmetry),因此在下文的分析中将省略角标i。为了建立更为精确和便于分析计算的数学模型，本文做如下假设:

假设2②假设2保证合同会给所有成本类型的投标者。是关于θ的一个递增函数。

假设3：采购者一定是通过采购拍卖来采购标的（即使出现最高成本ˉ）。

本文用S(q，p)=s(q)-p代表第三方评价规则，其中s(q)是第三方对于产品质量的评分。本文假设所有的投标者在投标前知道这个评价规则而且采购者承诺该评分规则代表了他的最优偏好。本文假设该评分规则具有如下性质:

假设4 ：这里s(q)-c(q，θ)对于所有的关于q有唯一的极大值，s(.)是递增的关于q≤argmax{s(q)

本文将引入Arrow-Pratt完全风险厌恶度量（Arrow-Pratt measure of absolute risk aversion）来定义市场中的风险厌恶投标者。

定义1[8]：本文称投标者期望效用函数Ub(x)的Arrow-Pratt完全风险厌恶度量有如下定义:

定义2[8]：假如投标者期望效用函数Ub(x)的Arrow-Pratt完全风险厌恶度量A(x)＞0,则称该投标者是风险厌恶的。

2 模型分析

本文将讨论风险厌恶对多属性采购拍卖投标策略的影响。由于投标具有二维属性，因此需要分析风险厌恶对于每个指标的影响。首先，本文考虑风险厌恶对于价格属性投标的影响。由上文可知采购者通过第三方评分的方式来确定投标获胜者。对于投标者来说，他们竞争中有三种方法可以提高得分增大自己的获胜概率。这三种方法分别是：（1）提高产品质量得分；（2）降低价格；（3）既提高质量又降低价格。根据假设4和第三方评分规则S(q，p),投标者对于均衡质量投标有如下选择:

引理1：在多属性第一和第二评分采购拍卖中，投标者将选择qs(θ)作为均衡质量投标:

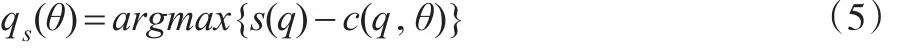
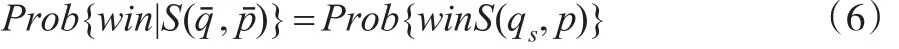
因此，投标者的期望效用为：

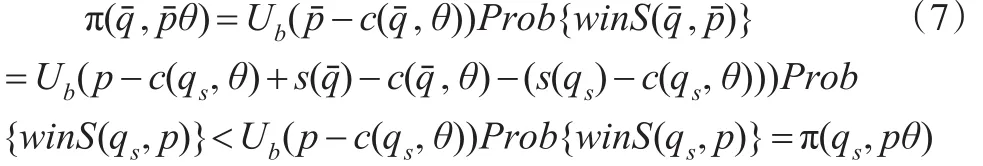
上述不等式表明对于投标者来说不存在另一个均衡质量投标。证毕。

上述引理表明在期望效用函数作用下，质量属性的选择与价格属性选择是独立的，本文可以通过先求解最优的非价格属性，本质上将多属性拍卖转化为传统的单属性拍卖。下面将讨论风险厌恶投标者均衡价格的策略。

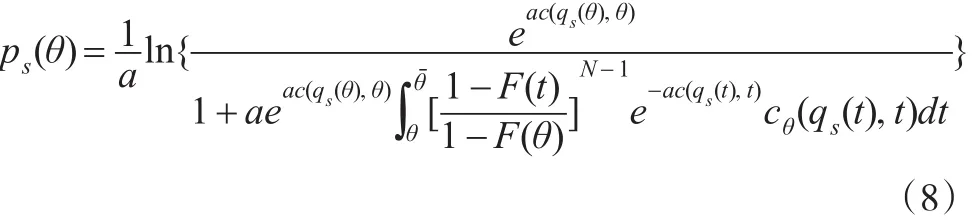
在多属性第二评分采购拍卖机制中，投标者的均衡投标价格为：

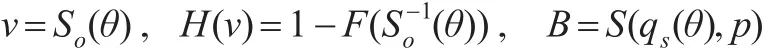
因此在多属性第一评分采购拍卖中，投标者的目标函数可以表示为:

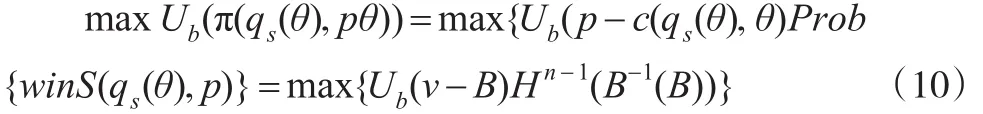
本文令G(.)=(1-F(.))n-1,g(.)=G′(.)那么式（10）可以变为：

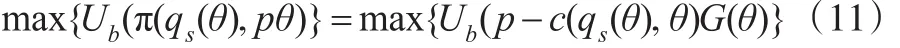
由包络定理以及一阶最优性条件，有如下微分方程：

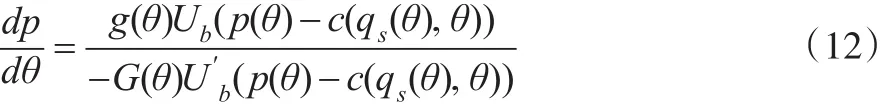
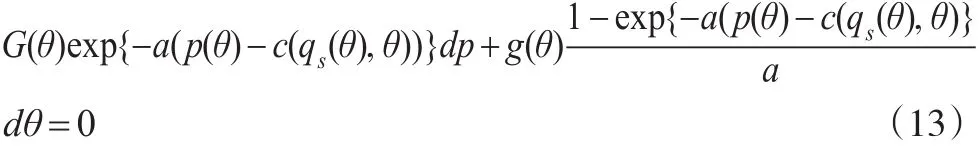
通过计算可以知道上述微分方程有积分因子eac(qs(θ)，θ)，因此本文可以将方程（13）变为下述微分方程：

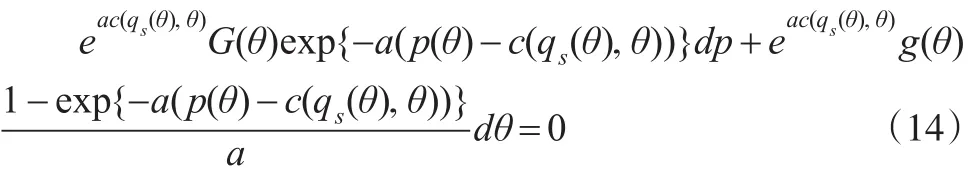
显然上述方程是一个恰当方程，本文利用边界条件解方程（14），得到投标者的均衡价格策略为：

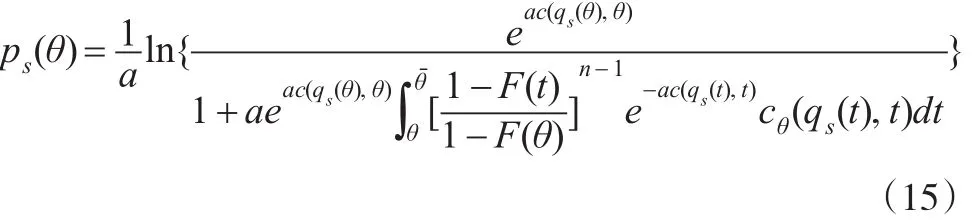
对于多属性第二评分采购拍卖，由文献[9]命题4的主要结论，可知：

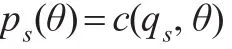
证毕。

上述命题的主要结论表明投标者的风险厌恶对于多属性第一评分采购拍卖机制的均衡价格产生了影响，而对多属性第二评分采购拍卖机制的均衡价格没有产生影响。当投标者知道自己的效用函数时，能够得到自己均衡价格的解析表达式。通过等式（15），可以知道该均衡价格和参与投标的人数是相关的。在其他条件固定的情况下，均衡价格将随着投标者人数的上升而下降。接下来将讨论风险厌恶程度如何影响多属性第一评分采购拍卖机制的均衡价格。

命题2：设是另一个效用函数，满足函数Ub的所有假设，̂为的风险厌恶度量。在多属性第一评分采购拍卖中，如果有那么投标者的均衡价格就有下述关系:

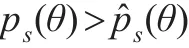
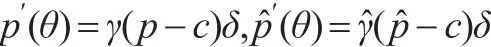
本文令使得上述不等式成立的所有θ构成的集合为S。而当θ=θˉ,可以知道：

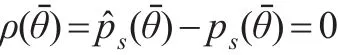
因此必然存在θ*=maxS和ε＞0,对于任何θ∈(θ*-ε，θ*+ε)，有：

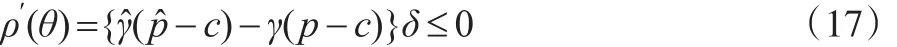
由于δ(θ)＞0,那么可得：

又由函数γ(.)的定义，可以知道γ′=1+αγ。对于任意t≥0,有γ(t)≥0,进而那么γ(.)是一个严格递增函数。结合归纳假设式（16）可得：

结合不等式（18）和式（19），可得：

另一方面，由文献[4]知道如果â＞a，则有：

显然不等式（20）和式（21）将导出矛盾，即假设是错误的。因此有：

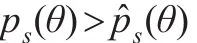
证毕。

上述命题的结果说明，在多属性第一评分采购拍卖中，在其他条件不变的条件下，均衡价格随着投标者风险厌恶程度增大而降低。

3 结论

在基于第三方评分的条件下，本文研究了带有风险厌恶投标者的多属性采购拍卖模型，给出了投标者的均衡投标策略，分析了投标者的风险厌恶程度以及参与投标的人数对于投标策略的影响。本文的主要结果将已有文献[1，7]中相应结果推广到更一般的情形。通过对本文主要结果的分析，可得如下结论:当投标者的风险厌恶程度或者投标者人数分别增大时，投标者的投标价格会降低；而对多属性第二评分采购拍卖不会带来影响。因此面对风险厌恶的投标者时，采购者选取多属性第一评分采购拍卖机制获得的效用优于选取多属性第二评分采购拍卖机制获得的效用。