基于马尔可夫链的装备技术成熟度评估方法

2019-03-14宋敬华郭齐胜

火力与指挥控制 2019年2期

李亮，宋敬华，郭齐胜

（陆军装甲兵学院，北京 100072）

0 引言

评估在日常生活中扮演着重要的角色。人们经常希望通过比较不同事物的优劣以作出正确的决策。对于构成装备及装备体系的关键技术也是如此，成熟度评估是评价不同关键技术好坏的重要手段之一。

现代武器装备技术水平进行综合评价的目的，是要回答武器装备的先进程度如何，其简单的评价指标是先进、一般和落后。但是，由于武器装备技术是不断发展的，进行评价的参照系是随着时间的推移而不断变化的，也就是说，对武器装备的技术水平进行评价不能脱离时间这个因素。

成熟度评估的结果经常有时滞。因此，依据评估结果所做的决策也有时间上的滞后。本文尝试提出一种基于马氏链的成熟度评估方法以解决这个问题。将关键技术成熟度的评估值作为一个马尔可夫链，初始分布和转移概率矩阵可以通过统计计算得到。进一步可以通过计算得到成熟度的稳态分布。将成熟度的数学期望作为成熟度的评估值。基于初始分布、转移概率矩阵和稳态分布的计算可以分别得到成熟度的初始值、演化值和稳态值。可以通过成熟度评估次数的增加，不断更新转移概率矩阵的信息，从而更新成熟度的评估值以保证评估结果的准确性。

1 马尔可夫链与成熟度评估

成熟度评估存在时滞问题，针对时滞可采用马氏链方法进行解决。本节主要对成熟度评估的时滞问题和马氏链的基本理论进行分析。

1.1 时滞问题

本文所谓的时滞有两方面含义：一方面评估结果有时滞；另一方面决策有时滞。

1）时间与空间无时无刻不在变化。基于这样的事实，对传统评估方法而言，当经过一系列复杂的过程得到评估结果时，被评价对象的状态已经发生改变。这样一来，评估结果有了时间上的滞后，即评估的时滞。

2）所谓的决策时滞是指由于评估的时滞，基于评估结果所作出的决策也不可避免地具有时滞和误差。这样一来决策也就有了时间上的滞后。

1.2 解决方案-马尔可夫链

事物的发展，是多层次的随机事件与必然事件相互交替和相互作用的过程。虽然个别随机事件在某次试验或观察中可以出现也可以不出现，但在大量试验中它却呈现出明显的规律性-频率稳定性［1］。下面对相关概念进行介绍［2-4］。

1.2.1 有限状态齐次马尔可夫链

给定σ-域B上的状态空间S，一个由在S中取值的随机变量 ξn组成的随机过程{ξn，n=0，1，2，…}称为马尔可夫链，如果对每一个非负整数n和集合T∈B，几乎处处成立

当 P{ξn+1∈T|ξn}不依赖于起始时刻 n 的取值，则称之为齐次马尔可夫链。当S是一个有限集合时，称之为有限状态齐次马尔可夫链（马氏链），式（1）称为马尔可夫性（马氏性）。

1.2.2 平稳分布（不变测度）

称概率分布{πi，i∈S}为马尔可夫链ξ的平稳分布，如果

式（2）可以表述为向量形式

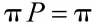
1.2.3 基本假设

当对一个系统进行评估时，第k+1次评估的结果仅与第k次的有关，而与第k次之前的评估结果无关。换句话说，专家对每个指标的打分具有马尔可夫性。如果打分值在整数集中取值且与起始时刻无关，那么每个指标的分值组成的随机过程就是一个有限状态齐次马尔可夫链。

在如上假设条件下，马尔可夫链的相关理论就可以用来解决涉及专家打分评估的相关问题。马氏链中初始分布的概念可以用来刻画指标得分的初始出现频率。转移概率矩阵的概念可以用来描述第k+1次评估和第k次评估之间的关系。对打分结果的统计分析恰好可以描述指标权重的当前状态；借助转移概率矩阵，又可以得到指标权重的演化趋势；最后，平稳分布的概念可以用来确定权重的稳态值。

首先，初始权重可以通过计算指标打分值的频率来获得；其次，指标权重随着时间推进的演化趋势可以通过转移概率矩阵的相关运算得到；最后，各个指标最终的稳态值可以通过平稳分布的相关计算进行确定。

根据初始权重（通常是传统方法所得到的评估结果），决策者可以像往常一样作出他们的决策；根据权重的演化趋势，决策者可以了解评估结果的变化趋势。最终，再结合稳态分步的结果，由于评估结果时滞的减小，并且系统的当前状态及演化趋势已知，决策者的决策误差也就有了相应减小的可能。

基于马氏链的评估方法过程简单、模型通用，下面将用来消除成熟评估过程的时滞，建立基于马氏链的成熟度评估方法

2 基于马尔可夫链的装备技术成熟度评估

建立基于马尔可夫链的成熟度评估方法，需要一些合理的假设和适当的准备工作。本节还将对所提出方法的具体步骤、与经典模型的比较、向技术体系成熟度评估的推广进行分析。

2.1 基本假设

根据1.2节中的基本假设，得出如下的基本假设：

1）假设第k+1次成熟度评估的结果仅与第k次成熟度评估的结果有关，而与之前的评估结果无关。这其实是比较符合实际的，因为假设某一技术在k时刻处于TRL2，那么在k+1时刻，正常情况下它不依赖于之前k-1时刻的成熟度等级，最起码他不会回到TRL1。这样一来，根据相关定义，TRLs和IRLs就具有了马尔可夫性。

2）某项关键技术的发展及其与其他关键技术之间的交互存在可循的规律。

正如恩格斯所指出的，表面上是偶然性在起作用的地方，这种偶然性始终是受内部隐蔽着的规律支配的，而问题只是在于发现这些规律。技术发展规律的分析思路是分析现状、趋势、对比找出不足。在假设1）条件下，考虑到成熟度等级的有限状态（一般为5、7或者9状态）以及它的状态转移与起始时刻无关（齐次性），有限状态马尔可夫链的相关理论，可以用来描述并解决技术成熟度评估、集成成熟度评估和系统成熟度评估的问题。

2.2 准备工作

为了用马尔可夫链的相关理论来解决成熟度评估的时滞问题，需要做一些前期的准备工作。

1）确定技术成熟度和集成成熟度的状态空间

为了方便起见，将成熟度等级记为{m0，m1，…，mn}，这样一来，n级的标度及组成了一个状态空间。

2）获取TRL/IRL的初始分布

对第k次和第k+1次成熟度评估数据进行统计分析，初始分布可以表示为：

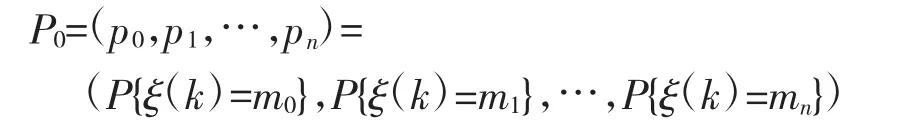
其中，P{ξ（k）=ml}=n（ml）/∑n（ml）（l=0，1，…，n），即P{ξ（k）=ml}表示的是成熟度 ml在第 k 次成熟度评估中出现的频率。

3）进行进一步的统计分析以获取TRL/IRL的一步概率转移矩阵

计算成熟度从状态i到状态j转移的概率，作为概率转移矩阵P中的元素pij，P=（pij）（n+1）×（n+1）。

完成以上工作以后，初始成熟度、演化成熟度就可以进行计算了。实际上，成熟度被认为是他们自身的数学期望。

初始成熟度计算如下：

r步转移后的演化成熟度计算如下：

为了计算稳态的成熟度，首先要得到稳态分步。稳态分步可以通过求解如下方程组得到。

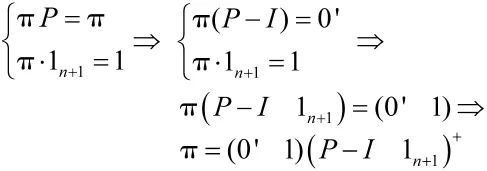
其中，1n+1=（1，…，1）'；0=（0，…，0）'；P=（pij）（n+1）×（n+1）；（·）+表示的是矩阵“·”的 Moore-Penrose广义逆矩阵（因为它的存在性和唯一性）。

这样，稳态成熟度的计算如下：

2.3 具体步骤

模型流程如图1所示。

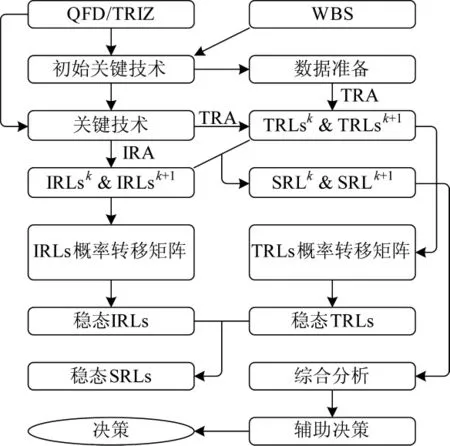
图1 基于马氏链的SRA方法流程图

1）关键技术CTEs获取

CTEs通过QFD/TRIZ/WBS进行获取。通过WBS可以获取初始的CTEs，借助QFD/TRIZ的帮助，可以获取CTEs的权重［5-6］。综合考虑可以得到系统的关键技术指标CTEs。

2）初始IRL/TRL获取和初始SRL的计算

邀请若干评估小组分别进行成熟度评估。记录初始的TRL/IRL及相应的SRL。为了进行评估的方便，设计如图2（表示CTEi的技术成熟度是TRLi，CTEi和CTEj的集成成熟度是IRLij）所示的表示方式。

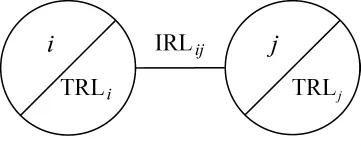
图2 TRL/IRL关系示意图

假设有n个CTEs，TRL=（TRLi）n×1，IRL=（IRLij）n×n，SRL=（SRL）1×1，那么 TRL/IRL/SRL 的关系可以用公式表示如下：

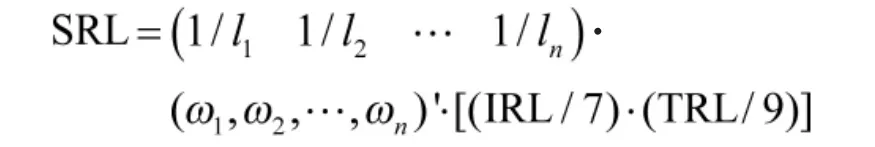
其中，li（i=1，2，…，n）表示的是和CTEi有集成关系的CTEs的个数（包括CTEi本身在内）；ωi（i=1，2，…，n）表示的是CTEi的权重。

根据式（5）和TRL/IRL/SRL的初始状态可以获取：。

3）进行第k次成熟度评估

邀请相同数目（尽量和之前相同）的评估小组进行第k次成熟度评估。将评估数据记为：和。

4）进行第k+1次成熟度评估

邀请相同数目（尽量和之前相同）的评估小组进行第k+1次成熟度评估。将评估数据记为：TRLk+1=，和。

5）获取一步转移概率矩阵

通过对各成熟度的转移频率进行分析，分别获取TRL和IRL的一步转移概率矩阵。

6）求解稳态分步

通过求解式（3），可以得到TRL和IRL的稳态分布TRLs和IRLs。

7）稳态TRL/IRL获取与SRL计算

根据式（4），计算稳态 SRL。

8）结果对比分析并作为决策支持

将初始的、演化的和稳态的SRL进行对比，得出的相关分析结果可以作为决策支持。

2.4 和经典模型的比较

1）从成熟度获取方面。基于马氏链的系统成熟度分析模型通过初始分布、转移概率矩阵和稳态分步获取3种形式（初始、演化、稳态）的成熟度；经典模型仅能通过简单的统计分析或数学计算获取一个成熟度数值。

2）对时滞的处理方面。基于马氏链的模型通过转移概率矩阵和稳态分布来解决时滞问题；经典模型对时滞问题基本没有考虑。

3）从短板的避免方面。对于每一项CTE在装备发展的不同阶段通过不同的阈值（短板的底线）来进行约束，从而避免单项技术短板的出现。同时，由于IRL的引入，还可以克服集成过程中可能出现的“集成短板”，这一点是传统方法不容易实现的。

综合来讲，由于马氏链模型的采用从某种程度上可以降低系统设计中的风险，决策者的决策变得更加准确和科学。

2.5 向技术体系成熟度评估的推广

引入系统集成成熟度（System Integration Readiness Level，SIRL）的概念，用于衡量不同系统（System）之间集成成熟度，并用于计算技术体系成熟度（Technical System of System Readiness Level，TSoSRL）。

其中，hi（i=1，2，…，n）表示的是和Systemi有集成关系的 System的个数（包括Systemi本身在内）；μi（i=1，2，…，n）表示的是 Systemi的权重；m 表示的是系统集成成熟度的分级；SRL/1中的1是因为SRL是［0，1］之间的一个数。

通过类似技术成熟度到系统成熟度的步骤，就可以通过系统成熟度和系统集成成熟度获取技术体系成熟度。

3 应用示例

为了验证基于马氏链的方法的科学性和可行性，下面给出一个基于马氏链的系统成熟度评估的例子。

1）通过WBS/QFD/TRIZ过程，得到4项关键的装备技术。第k次和第k+1次评估结果（评估小组由4个专家组成）分别如图3和下页图4所示。

图3 第k次评估结果

为了计算的方便，将图3和图4转化为表格形式，如下页表1～表4所示。

2）根据马氏链相关公式进行数据分析，将一些关键结果列在下面。

图4 第k+1次评估结果

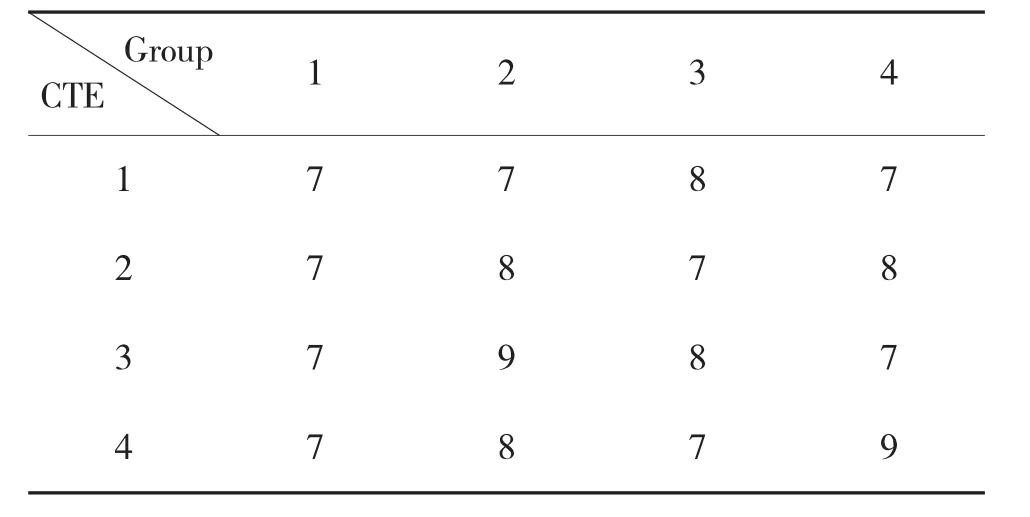
表1 第k次评估的技术成熟度

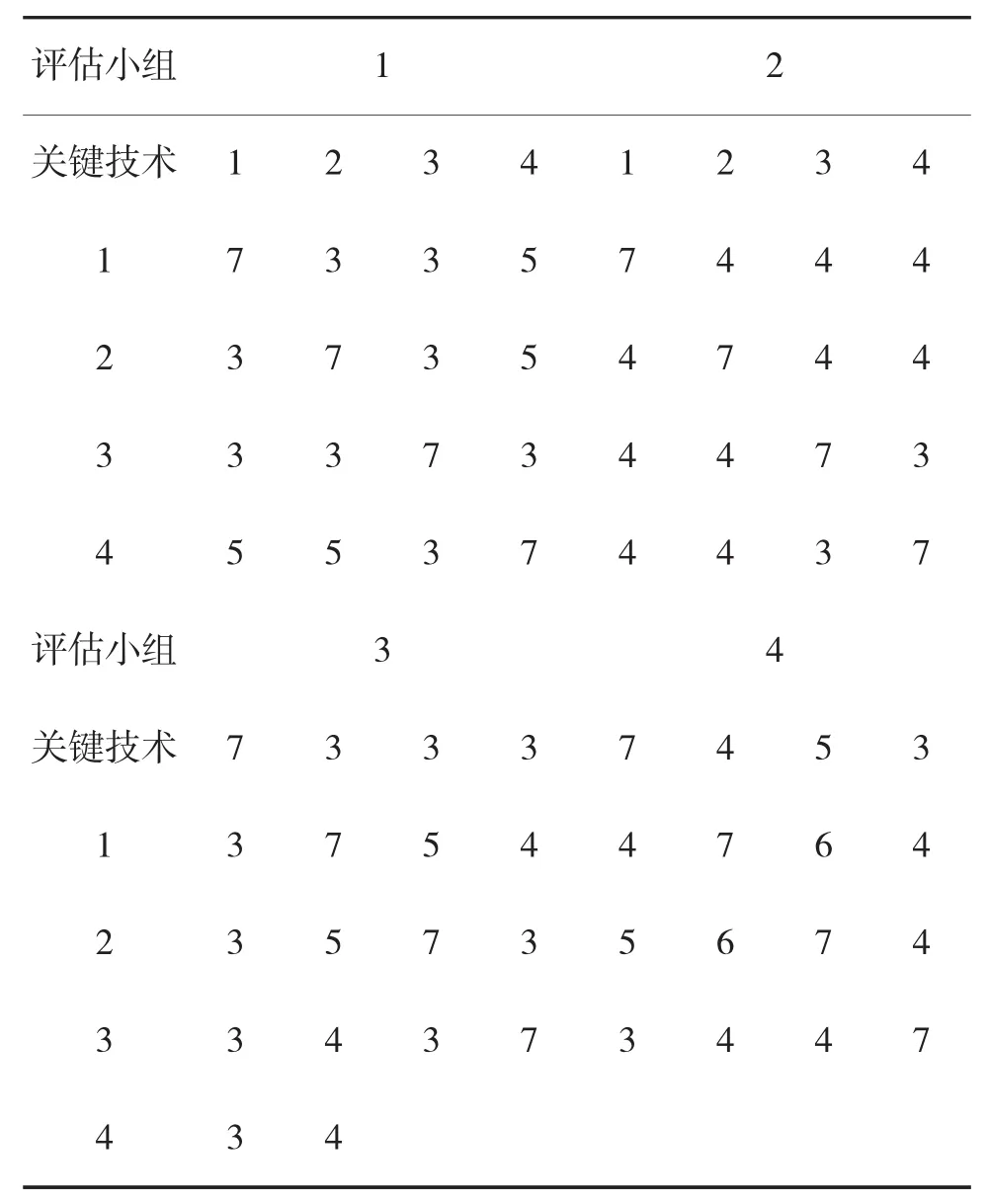
表2 第k次评估的集成成熟度

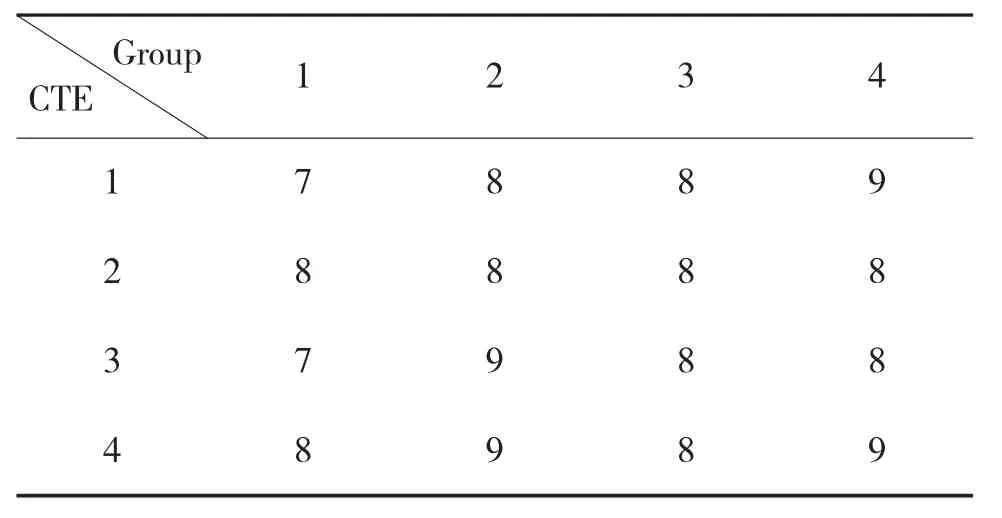
表3 第k+1次评估的技术成熟度

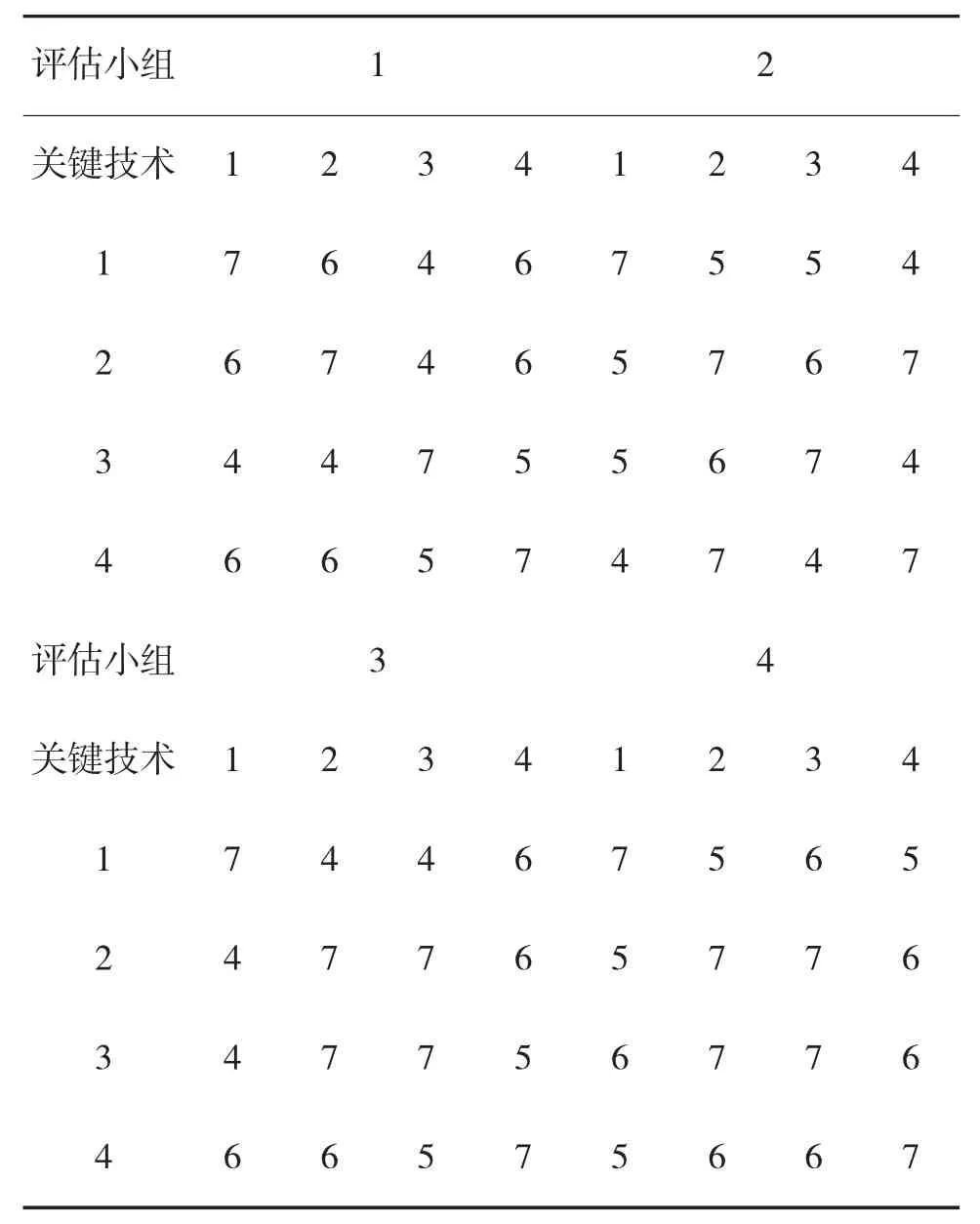
表4 第k+1次评估的集成成熟度

为了更加形象地展示成熟度在不同转移步数时的状态，分别将技术成熟度、集成成熟度和系统成熟度转移步数的变化规律绘制成散点图，如下页图5～图7所示。

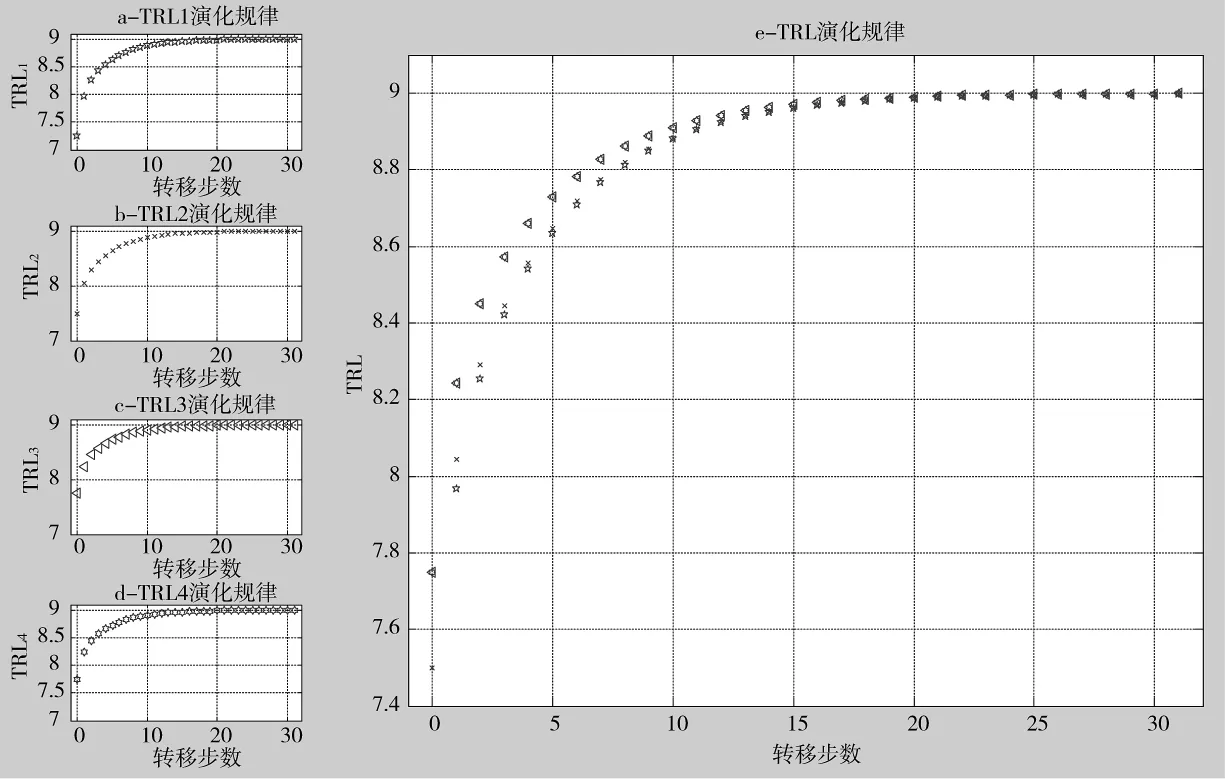
图5 TRL演化规律

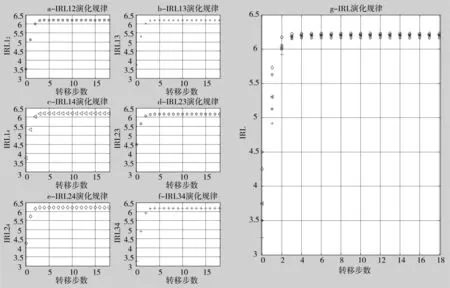
图6 IRL演化规律

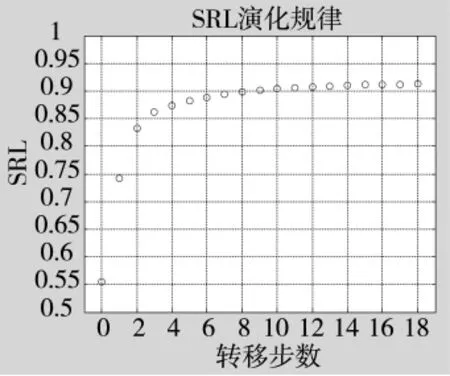
图7 SRL变化规律

从图5～图7中可以看出，在初始阶段，TRL1TRL2TRL3=TRL4并且有SRL=0.555 7；在稳态阶段，TRL1=TRL2=TRL3=TRL4并且有SRL=0.914 3。从中可以看出，如果仅仅按照传统方法（即初始状态成熟度SRL-1）进行决策，则可能会拒绝这一技术方案；但是如果参考稳态的成熟度数值（SRL-5）及到达稳态所需的转移步数（本例大约9步即可到达0.901 2，如图7所示），则有很大可能会接受这一方案。拒绝一个可行的方案将是十分可惜的。基于马氏链的评估方法减少了时滞对决策的影响，从而降低了决策的风险。以上示例证明，方法是科学可行的。