课程再设计，让儿童生命与数学和谐共振

■江苏省海门市第一实验小学 张海红

一、理顺逻辑结构

数学学科是一门逻辑性极强而又极其追求简约的学科，因此每一个新的数学概念的诞生都有着不得不诞生的理由。作为数学教师，我们在教学新内容时，往往要追问自己，为什么要让孩子学习这个内容？或者说这个知识点的价值何在？例如“比”，用分数、用除法都可以对两个数量进行比较，为什么还要用到“比”？通过研究知道：比不仅可以对两个数量进行比较，还可以同时对两个以上的数量进行比较，如配制一种混凝土，水泥、石子、黄沙的比是4∶3∶2。想到这点，那么课堂教学设计自然就关注到了“比”概念产生的价值。因此，在教学之前不妨多问问这样的问题，想明白了，也就理顺了知识之间的逻辑结构，而这种逻辑结构往往又与儿童的认知心理相吻合。以此做出的教学设计，逻辑清晰，过程简约，数学味浓，不失为一堂好课。再如，加法和乘法运算定律的教学，教材上都安排先学习交换律，再学习结合律，这自然是遵循认知规律，由易而难的，但是知识发生的顺序究竟是怎样的呢？学习运算律最重要的意义是解决简便运算的问题，而简便运算的重要思想方法是凑整，即把能够凑成整十、整百、整千等的数结合在一起先计算，再加或乘另外一个数，会使计算简便。但是在实际操作中，有时想凑整的两个数不在相邻的位置，为了使它们能先算，就需要其中的一个数和其他的数交换一下位置，于是交换律登场。据于这样的理解，课程设计可以先安排学习结合律，并理解结合委的意义和价值，然后再制造认知冲突，如果想凑整的两个数不在相邻的位置怎么办？引导学生根据已有的运算经验，想到交换数的位置的办法，点明这就是交换律。这样的教学从教材既定的框架中跳出来，重构了另一条学习线路，即重新经历知识发生发展的过程，更深刻地体悟学科发展的意义及价值，引导学生进行创造性思考。

二、力求知识延展

物体在外力作用下能延伸成细丝而不断裂的性质叫延性；在外力（锤击或滚轧）作用能碾成薄片而不破裂的性质叫展性。延展性好的物质更容易被塑形后创造出更多的新产品。安德烈·焦尔当在《学习的本质》一书中指出：“学习首先是一种变形。”知识变形的前提是该知识有较好的延展性。我们追求知识的延展，即是追求从一个核心知识衍生出更多的知识、能力、活动经验，甚至数学思想。此时，这个知识是活的，随时可以变形成新问题需要的结构。教学中，教师应当关注知识可延展的方向，并适当点拨，为知识即将可能的变形奠基。既然要变形，那么变形的基点在哪里？方向在哪里？这是教学中应当思考的。站在知识系统上方，整体审视教学内容，才能看清知识在结构中所处的位置及来龙去脉，才能知道教学应在哪里着力，哪里突破，哪里伏笔。例如《倒数的认识》。根据倒数的意义，两数相乘的积是1，这两个数就互为倒数。互为倒数的两个数的形式是多样的，可以是分数、整数，也可以小数等，而教材呈现的例子和练习都是求分数（不含带分数）和整数的倒数，实际教学是否要关注带分数、小数的倒数呢？我认为在儿童学习力许可的情况下，可以适当延展，毕竟生活中数的表现形式确实是多种多样的。因此在学生已经知道了倒数的意义和求分数的倒数的方法后，继续组织引导 学生尝试求出0.25、212的倒数。教师板演：

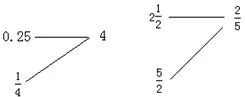
从而师生共同总结出同一个数的倒数可以有不同的表现形式，而这几种表现形式的值是相等的。

《倒数的认识》一课，从知识层面来讲，难度不高。主要是使学生理解倒数的意义，掌握求分数的倒数的方法，并能正确熟练地求出分数的倒数。通过对本节教材和后续教材的反复研读，以及对儿童的深入研究，我认为，本课教学重点应放在思维的提高上，这就需要对教材进行适度超越，对知识适当延展，体现在两个方面：1.让学生掌握了求小数和带分数的倒数；2.让学生明白了“同一个数的倒数的表现形式可能不止一种”的观点。而这两点对后续学习，尤其是学生的思维发展是非常有效的。事实上，对这两点，所有学生都能轻松地接纳并完成。我深信，这些孩子在遇到计算形如“19×0.25＋81÷4”时，就不会只想到按着运算顺序慢慢算，而会想到4 和0.25互为倒数，所以81÷4可以变形成为81×0.25，从而用乘法分配律简便计算。当然追求知识的延展性一定要把握“度”的问题，而这个“度”基于对儿童学习心理及能力的深度把握，在儿童可接纳的范围内延展。过度，数学课程就会显得艰涩而与儿童疏远；适度，则会引发儿童生命与数学课程契合共鸣。

三、整合关联领域

数学知识是一个庞大的知识系统，且在旧知识的基础上不断增长、不断深入，但始终具有一定的结构系列，这就是知识点的内在关联的根源和实质。所有的知识点具有互相支撑的关系。如下图中的知识X与A、B具有归属关系，知识X，是知识A、B的上位知识，反之知识A、B 是知识X 的下位知识。从上位知识到下位知识，一般可以通过演绎得到。而从下位知识到上位知识，一般可以通过归纳得到。再如知识A、B 是并列关系，从知识A 到知识B，可以通过类比（正类比、反类比）得到。

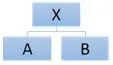
实际教学中，教师要研究知识之间的支撑关系，对关联领域适当整合，可以稳固知识结构。例如，加法运算是求两个不相交集合的并集，加法运算的本质是同类量的合并。整、小数加法计算法则：相同数位对齐；从低位算起；满十进一。相同数位对齐的意义就是使计数单位相同的数相加，如3 个一加5 个一，2 个0.1 加7 个0.1 等。分数加法法则：把异分母分数先转化成同分母分数，再相加。转化成同分母分数的意义就是使两个分数的分数单位变成相同，以满足相加的条件。

在关于加法运算的例子中，加法运算的意义和本质是上位知识，也是一般模型，而整、小数加法运算和分数加法运算是加法的三个特例，是下位知识。基于儿童学习特点，教材按这样的顺序组织：先安排学习整数加法运算，而后在与整数相加法的类比中学习小数加法计算，最后再安排异分母分数加法计算学习。作为教师，如果能谙熟加法运算的本质联系，就能透过教材的组织关系，轻易地找到知识之间的支撑关系，并强化旧知的支撑作用，高效完成新知建构。再如，苏教版五年级上册“小数乘法”单元安排了“一个数乘10、100、1000 后小数点位置变化”的学习，而在“小数除法”单元安排了“一个数除以10、100、1000后小数点位置变化”的学习。如下图：

通读教材后，我认为“一个数除以10、100、1000后小数点位置变化”的学习可以前置，只要在“一个数乘10、100、1000 后小数点位置变化”的学习之后，用类比支撑一下，就可以完成学习。

教师可以这样引导建立支撑：通过刚才的学习，我们知道一个数乘10、100、1000 后，小数点就会向右移动一位、两位、三位。我们还知道除法是乘法的逆运算，那么请你想一想，如果一个数除以10、100、1000，小数点会怎样移动呢？右与左互逆，于是学生马上会想到一个数除以10、100、1000，小数点会向左移动一位、两位、三位。这时再组织学生用计算器验证一下，进一步巩固即可。这样，在教师客观分析知识间的关系基础上，巧妙地用好这种关系，不仅可以稳固知识的结构，也可以节约课时，激起学生的自豪感。教材是课程标准的具体文本表现，是许多教育教学专家智慧的结晶，也是人类智慧的结晶，具有普遍性。教师的作用在于引导学生创造性地参与文本的意义生成过程，即重建文本的意义，并且根据儿童需要，对教材进行再度重构设计，大胆地进行“用课标教”的课程想象和实践，追求儿童与课程的真正和谐共振。