渗透化归，数形结合，落实数学抽象核心素养——“二元一次不等式（组）与平面区域”的教学和启示

■广西壮族自治区南宁市第三十三中学 黄 荣

在普通高中数学课程标准修订（2017 版）中指出：数学抽象是通过数量关系与空间形式的抽象，得到数学研究对象的素养。本文主要从“二元一次不等式（组）与平面区域”这节课的教学设计上，阐述如何让学生通过数量关系与空间形式的抽象，提升他们的数学抽象核心素养。“二元一次不等式（组）与平面区域”是人教A版《普通高中课程标准实验教科书·数学5（必修）》第三章不等式的第3 节二元一次不等式（组）与简单线性规划问题，第1课时内容，其相关概念是将一元一次不等式抽象出几何背景，再以几何直观推理的方法解决二元一次不等式的解集问题，它是线性规划问题的基础和前提，为后面寻求线性规划“最优解”奠定了基础。

一、教学设计及课堂实录

（一）创设情景，引入新知

数学源于生活又服务于生活，让学生从生活中的具体实例入手，由文字语言转化到符号语言，建立起二元一次不等式的概念，使学生经历、体验从实际问题中得到二元一次不等式（组）这一数学模型的抽象过程，让学生从已知到对未知的冲突，从而引出本节课要研究的对象。例：某高中食堂主要以面食和米食为主，面食和米食中的蛋白质和淀粉含量如下表所示。学校要求食堂给学生配置成盒饭，每盒至少有8 个单位的蛋白质和12 个单位的淀粉，请问食堂应该如何调配面食和米食分量呢？

设每份盒饭中面食为x百克，米食为y百克。

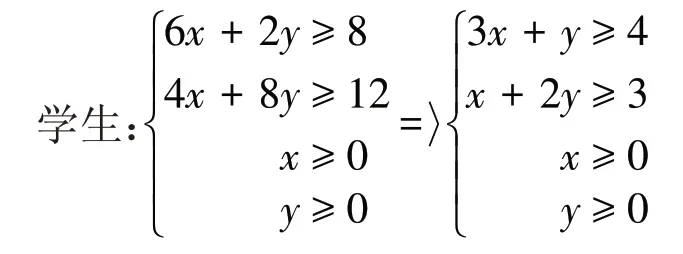
（得出二元一次不等式（组）的概念）

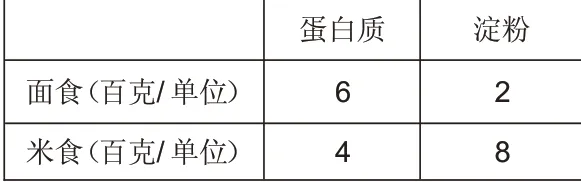
面食（百克/单位）米食（百克/单位）蛋白质6 4淀粉2 8

教师：如何求二元一次不等式（组）的解（集）？如果将有序实数对看做点坐标，那么二元一次不等式（组）的解（集）又表示什么图形？

（二）类比旧知，由数抽象出形

二元一次不等式表示什么样的平面区域？这是一个比较抽象的问题，学生需要通过已经学习过的、熟悉的知识进行类比、对接。这时，教师把知识建构的主动权交还学生，设置好梯度，以问题的形式引导学生自已探究完成，整个过程循序渐进，由具体一元一次到二元一次，由特殊点转化到形，借助几何画板直观形象展示，由浅入深，环环相扣，让学生在探究中完成由数到形自然抽象过程.

教师：一元一次不等式的解集可以表示为数轴上的区间，那么二元一次不等式（组）的解集表示什么图形呢？

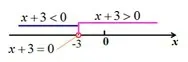
具体实例：在数轴上画出一元一次不等式x+3＞0的解集。

教师：那么，二元一次不等式又表示什么样的图形呢？

探究具体实例：二元一次不等式2x+y-6＜0 的解集表示什么图形。

学生探究活动一：

①设点P（x，y0）是直线2x+y-6=0上的点，求出相应的y0；

②在①的基础上，横坐标不变，选取适当的y1使得A1（x，y1）满足2x+y1-6＜0；

③在②的基础上，取x=-2，选取适当的yi，使得Ai（x，yi）满足2x+yi-6＜0；

④将点A描绘到坐标系中。

学生思考：①当点A 与点P 有相同的横坐标时，从数来看，它们的纵坐标有什么关系？

②从形来看，点A与直线有什么位置关系？

学生：那么是不是可以画更多的点来验证，满足2x+y-6=0的点都在直线的左下方呢？

教师：这个可以通过几何画板随意取点，观察坐标实现。（请学生操作几何画板，同学们一起观察数与形的关系。）

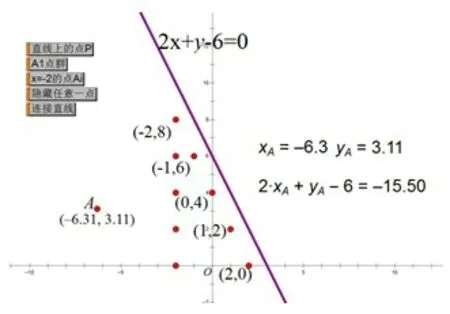
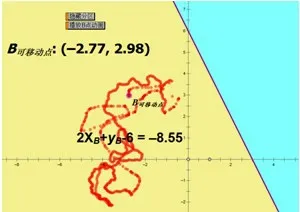
学生探究活动二（分组探究）：证明直线2x+y-6=0左下方所有的点的坐标都满足2x+y-6＜0。

学生：（通过探究活动一的启发，经过小组探究）将问题具体化，取直线2x+y-6=0左下方的任取一点A（x1，y1），过点A（x1，y1）做x 轴垂线与直线2x+y-6=0相交于点P（x1，y），这时后横坐标同为x1，由图形观察y1与y的大小即可得到结论。

教师：（完善证明过程），通过几何画板展示直线2x+y-6=0左下方任一点的运动轨迹，从而完善思维，实现由数向形的完全转化。

（三）由特殊到一般，生成概念

学生通过分析实际生活背景实现了由文字语言到数学符号的第一次抽象，再从两个探究活动中，通过观察——实践——猜想——验证，搭建了由感性思维到理性思维的桥梁，从事物的具体数学符号中抽象出数学概念和规则，从而完成了第二次数学抽象过程。那么接下来将引导学生由特殊到一般抽象归纳出一般二元一次不等式的解与平面区域的联系，并用数学语言予以表达，使二元一次不等式的解与平面区域的对应关系的理论体系更加完备的同时提升学生数学抽象这一核心素养。

教师：通过以上的证明，我们可以对一般的二元一次不等式有什么认知呢？

(学生讨论)判断表示平面区域的方法：直线定界，特殊点定域。

（四）概念的深化与应用

教师：请同学们利用二元一次不等式（组）与平面区域的知识，解决最初的生活问题，画出相应不等式表示的平面区域。

在此环节，学生在学案上做图，利用希沃教学软件及时对练习错漏之处进行互评和订正。重点在于规范学生思维的有序性和解题表述的条理性。

二、教学启示

（一）教学设计的立意

本案例教学内容是在学习不等式、直线方程后学习，它既是这两部分内容的延伸和交汇，又是图解法解决线性规划的基础，具有承上启下的作用。旧教材将它安排在直线方程后学习，体现的是它与方程的联系，而新教材将它与不等式的知识结合在一起，整章知识凸显的是通过数学的直观性进行学习，将重要的不等关系都给出了相应的几何背景，从而弱化了以逻辑性推导为主的传统学习不等式的方式；在课堂教学中，紧抓概念的生成这一环节，在由二元一次不等式抽象出平面区域的过程中渗透化归、数形结合和特殊到一般的思想，不仅训练了学生计算、做图的基本能力和学生数形结合、等价转化等数学思想，还有效提升了学生数学抽象思维这一核心素养。

（二）多媒体辅助教学的优势

概念教学首要注重概念的生成这一重要环节，但是本学段的学生数形结合思想还不够完善，识图、画图能力欠缺，对平面点集与图象的对应关系理解不深，因此在本案例中，如果没有具体、形象的感知，概念很难从直观材料或者现实背景中抽象出来。为了帮助学生完成思维的转化，本案例多次使用了多媒体辅助教学。例如：在探究一活动中，利用几何画板取满足不等式2x+y-6＜0的点Ai群，让学生发现点Ai群都在直线2x+y-6=0的左下方时，会有学生提出疑惑，一些特殊的点能否就代表全部满足2x+y-6＜0的点都在相应直线左下方？这时再用几何画板取任意点，让学生取移动、去观察，就能在形象的基础上让学生得到结论，为下一步的证明打下基础。探究活动二的证明是本节课的一个难点，学生必须在活动一的基础上通过图形去感知和分析，证明出来后，教师再利用几何画板播放，直线两个区域点自由运动时所满足的不等式，那么二元一次不等式（组）与平面区域的这么一个抽象的数学概念就在形象生动的教学环境之下自然生成了。概念课教学是高中数学最重要的一部分，也是较为抽象的一部分，本文仅以“二元一次不等式（组）与平面区域”为例，浅谈了对数学概念教学和培养高中学生数学抽象这一核心素养的一点认识，希望能起到抛砖引玉的作用。