关于二元割圆序列的k-错线性复杂度
2019-03-13陈智雄吴晨煌
陈智雄,吴晨煌,2
(1. 莆田学院福建省高校应用数学重点实验室,福建 莆田 351100;2. 电子科技大学计算机科学与工程学院,四川 成都 611731)
1 引言
设有限域 Fp={0,1,… ,p-1},其中p为奇素数。g为模p的一个本原根。若r|(p- 1), 则r阶割圆类定义为
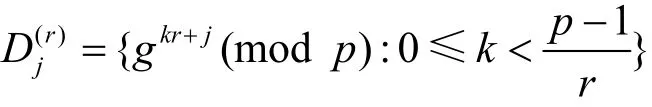
其中,j=0 ,1,… ,r-1 。易知,构成 Fp{0}的一个划分,并被广泛应用于定义伪随机序列[1]。
当r=2时,Legendre序列(su)[2-4]定义为

其中,u≥0。
当r=4时, Ding-Helleseth-Lam序列定义为
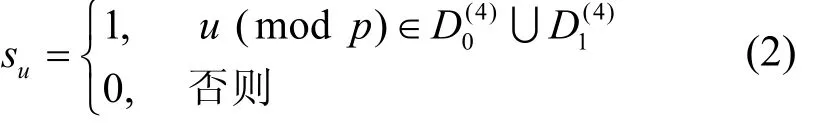
其中,u≥0。
当r=6且p形如24x+27,x∈ℕ时,Hall六次剩余序列(su)[6-7]定义为

其中,u≥0。
需要注意的是,在文献[6-7]中,g的选择需满足
上述几类二元序列已受到广泛的关注和研究。研究表明,这些二元序列具有好的伪随机特性,包括一致分布性、最优相关性、高的线性复杂度等[1-3,5,6,8-12]。Xiong等[13]证明了 Legendre、Ding-Helleseth-Lam二元序列的2-adic复杂度等于周期p。最近,Su等[14]基于Ding-Helleseth-Lam二元序列使用交织的方法构造了一个周期为4p的具有优的自相关值的二元序列。通常把上面这种Z*(p为素数)上的割圆类称为经典割圆类,对应的序列称为经典割圆序列,而把Zn*(n为合数)上的割圆类称为广义割圆类,对应的序列称为广义割圆序列[15-22]。
文献[23-24]把上述类型序列(su)视为p-进制序列并研究了其在有限域Fp上的k-错线性复杂度。但是,(su)在F2上的k-错线性复杂度还未彻底解决。文献[1, 25]证明了任意的非常数二元序列的k-错线性复杂度的一个下界。
命题 1([1,Theorem 3.3.1])对周期为p的任意非常数二元序列(su),其在F2上的k-错线性复杂度 LCk((su)) 满 足k<min{WH((su)),p-WH((su))}时,LCk((su))≥o rdp(2) 。其中,ordp(2) 表示2在模p的阶,WH((su)) 表示序列(su) 的一个周期中所含1的个数。
本文工作主要是考虑由经典割圆类定义的序列(su)的k-错线性复杂度。本文计算了 Legendre序列、Ding-Helleseth-Lam序列和Hall六次剩余序列在F2上的1-错线性复杂度,并限制2在模p的阶的某些取值,给出了这些序列在F2上的k-错线性复杂度的一些结果。周期序列的离散傅里叶变换在本文的证明中起到了关键作用。
下面介绍线性复杂度、k-错线性复杂度和周期序列的离散傅里叶变换等概念。
对于F2上周期为T的序列(su),其线性复杂度(记为LC((su)))定义为(su) 满足F2上的如下线性递归关系的最小阶L。
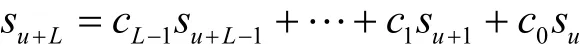
那么,(su)在F2上的线性复杂度可通过式(4)计算。
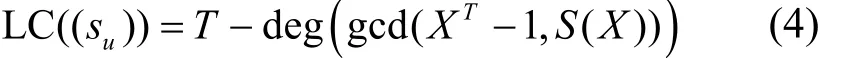
对于整数k≥0,(su)在F2上的k-错线性复杂度(记为LCk((su)))是指在序列的一个周期中改变至多k个元素后所得这些序列在F2上的线性复杂度的最小值[26]。即
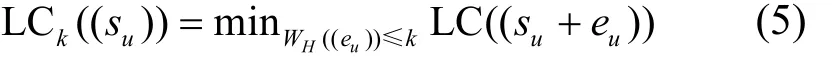
其中,(eu) 为周期为T的错误序列,WH((eu)) 为(eu)的一个周期中所含1的个数。k-错线性复杂度也被称为球体复杂度[27],本文不做详细描述。易知,LC0((su))= L C((su)) ,且
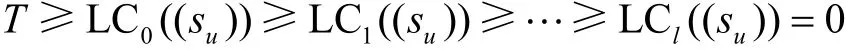
其中,l=WH((su)) 。
线性复杂度和k-错线性复杂度是序列的重要密码学性质,它们刻画的是序列的可预测性,从而衡量该序列是否适用于密码学领域。从密码学应用角度考虑,一个序列的线性复杂度应尽可能大,并且序列在改变若干项后其线性复杂度不应明显降低。
对于奇数T,序列(su)的离散傅里叶变换(ρ0, ρ1, … ,ρT-1) 和序列(su) 的线性复杂度具有紧密的联系。记m=o rdT(2)表示2在模T的乘法阶。对于T阶本原单位根 β ∈F2m,离散傅里叶变换(DFT,discrete Fourier transform)[28-29]定义为
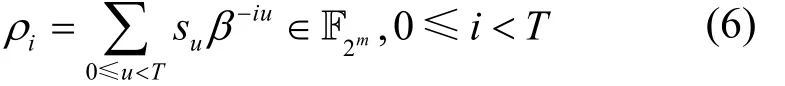
Blahut定理[30]给出了序列(su)的线性复杂度及其与DFT之间的关系,如式(7)所示。
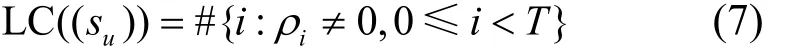
其中,#{⋅}表示集合{⋅}中的元素个数。

对于给定的β,G(X)在模xT-1下是唯一确定的,G(X)也称为序列(su)对应于β的defining多项式[34]。
2 离散傅里叶变换
Alecu 和 Sǎlǎgean[33-34]利用离散傅里叶变换给出了一个计算序列的k-错线性复杂度的近似算法。他们的方法有助于本文考虑 Legendre序列、Ding-Helleseth-Lam 序列和Hall六次剩余序列的k-错线性复杂度。本节计算了这些序列的离散傅里叶变换。更详细的讨论见文献[32]。
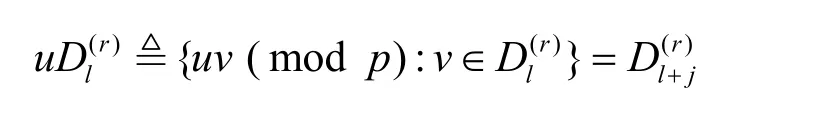
其中,u∈Dj。下文中D(r)下标的计算都是在模r下进行的,即对所有的0≤l<r,有定义
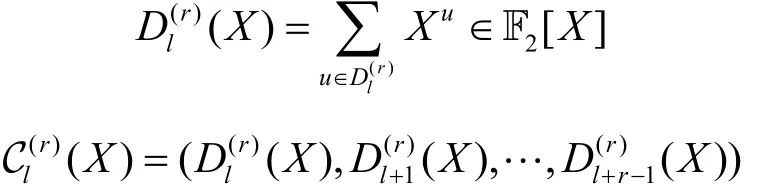
其中,0≤l<r。本文首先给出并证明如下关于内积计算的引理,其中0≤i,j<r。
引理1设β为F2的某一个扩域上的p阶本原单位根。对任意一对整数i,j满足0≤i,j<r,有
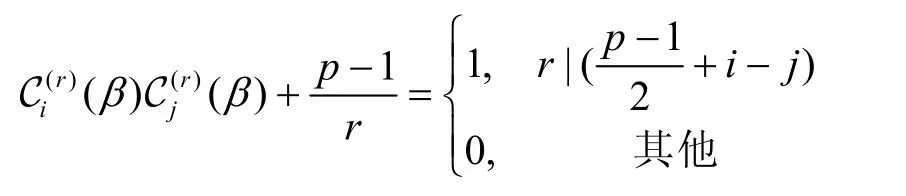
证明 对任意的0≤l<r,由于可得
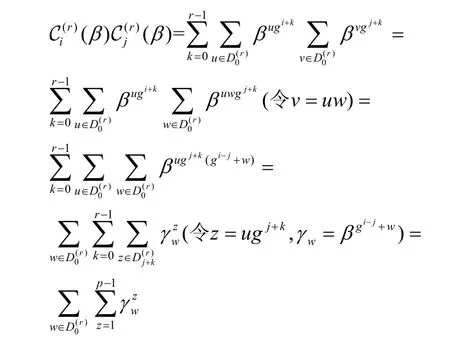
设ord(γw)表示γw的阶。由于β是p阶本原单位根,则有ord(γw) |p。若ord(γw)=p,则

若ord(γw)=1,则
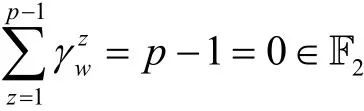
下面分别计算使ord(γw)=1和ord(γw)=p的元素的个数。
可以注意到ord(γw)=1当且仅当由于则也就 是说 , 存 在使等式成立,当且仅当i-j) 并且w是唯一的,因此,当时,有个元素满足ord(γw)=p,而只有一个满足ord(γw)=1。 若则对所有的
综上所述,可得
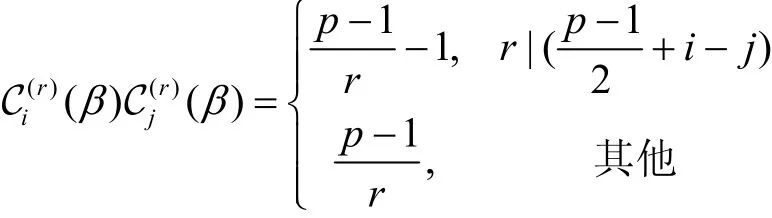
证毕。
下面给出Legendre序列、Ding-Helleseth-Lam序列和Hall六次剩余序列的Mattson-Solomon 多项式。
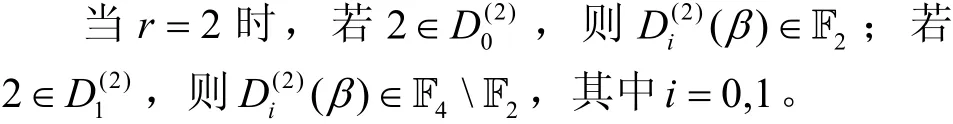
命题2设β为F2的某一个扩域上的p阶本原单位根满足:当当那么,式(1)定义的Legendre序列(su)的对应于β的Mattson-Solomon 多项式为
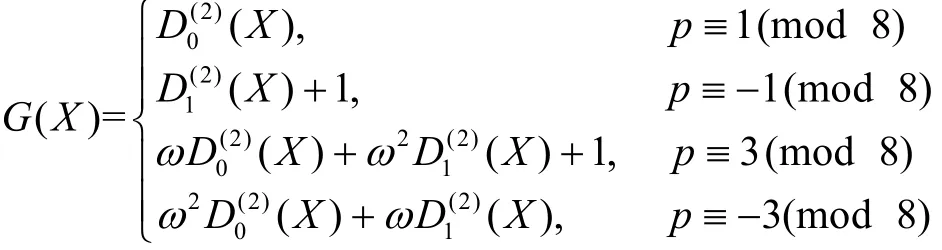
需要说明的是,当p≡ ± 1(m o d8)时,选择这样虽然得到不同形式的G(x),但是并不影响本文的讨论结果。
证明由引理 1可得式(1)定义的 Legendre序列(su)的Mattson-Solomon多项式为
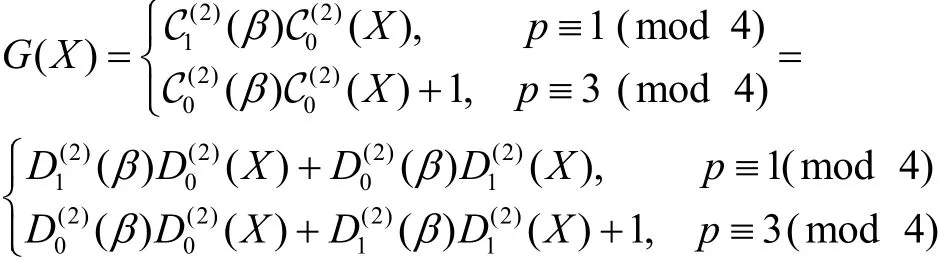
显然,在已知条件D0(2)(β) 的取值假设下,当p≡ 1(m o d 4)时,易知
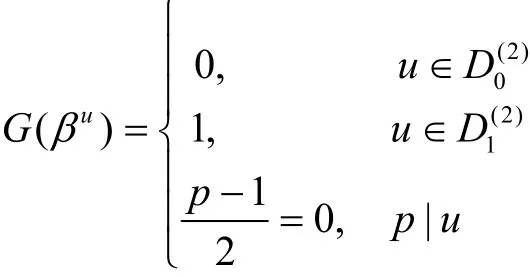
即su=G(βu),当u≥0。对于p≡ 3(mod 4)的情况可类似验证。
证毕。
由式(7)可得如下结论。
推论1[3]由式(1)定义的Legendre序列(su)的线性复杂度为
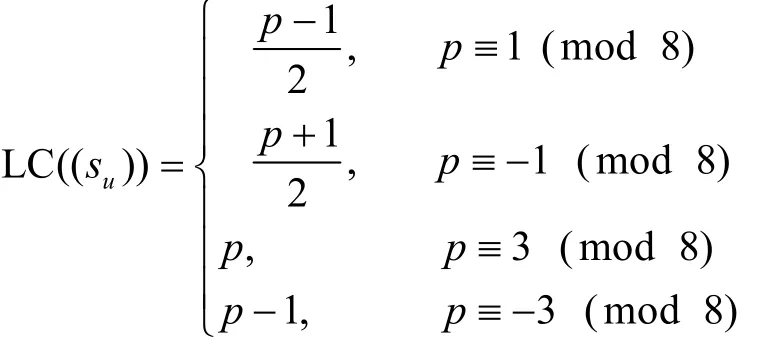
对于r=4的情况,由4|(p-1),则p满足p≡ 1(mod 8)或p≡-3(m o d 8)。由引理 1可知,由式(2)定义的 Ding-Helleseth-Lam 序列(su) 的Mattson-Solomon多项式如下所示。
当p≡ 1(mod 8)时,
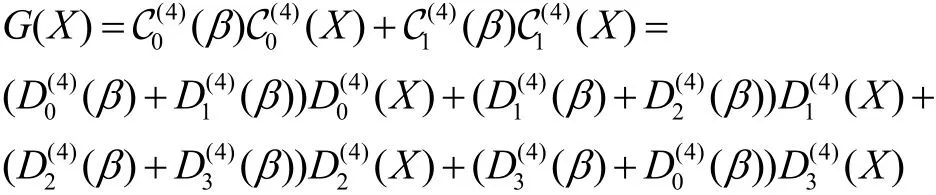
当p≡-3(mod 8)时,
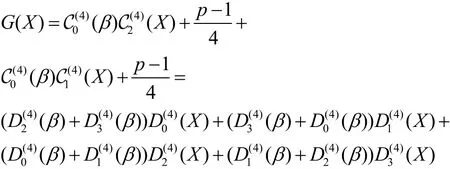
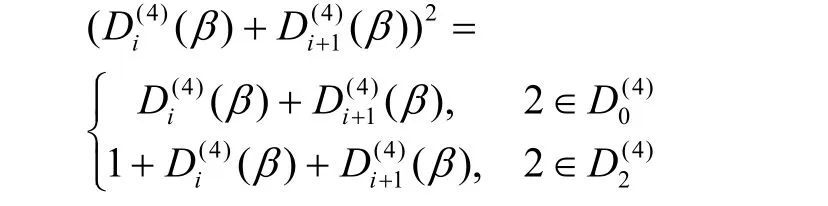
和

因此,可得
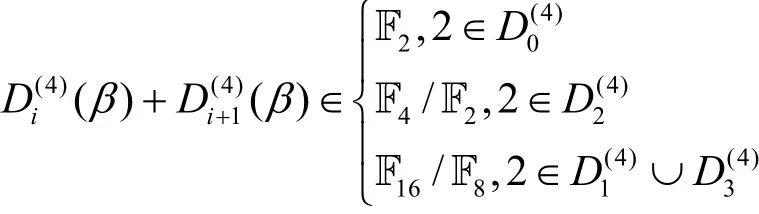
其中,0≤i≤4。
注意到,若p≡ 1(mod 8),则(即2 是模p的平方剩余),有综上所述,可得命题3。
命题3设β为F2的某一个扩域上的p阶本原单位根。
1)若p≡ 1(mod8),令则由式(2)定义的Ding-Helleseth-Lam序列(su) 对应于β的Mattson-Solomon多项式G(x)如下。
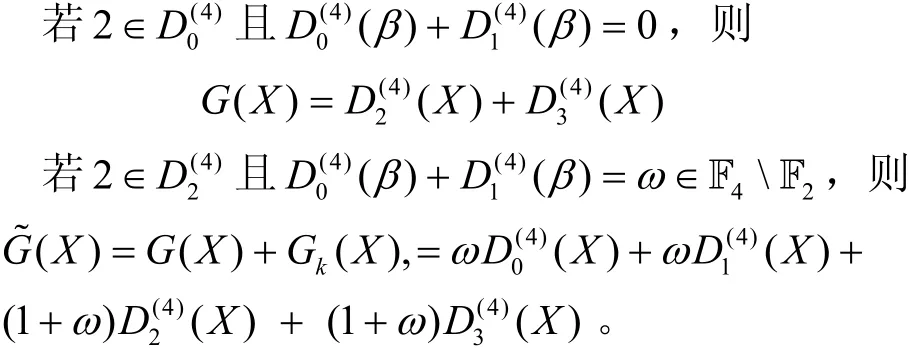
2)若p≡ -3(m o d 8), 令θ∈F16且 θ4=1+θ ,则 由 式(2)定 义 的Ding-Helleseth-Lam 序列(su) 对应于β的Mattson-Solomon 多项式G(x)如下。
若2∈D(4),则
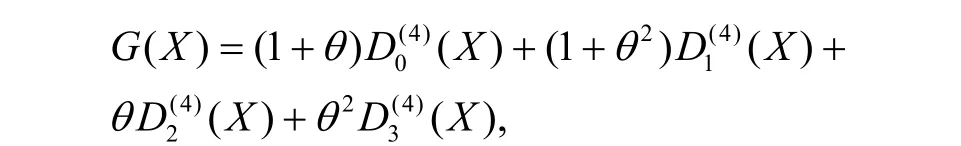
若2∈D(4),则
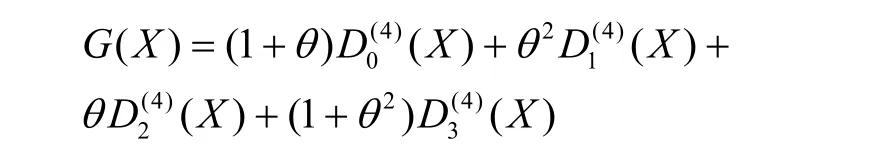
在命题 3 中,当p≡ 1(mod 8)时,若选择的其他取值,虽然得到不同形式的G(x),但是并不影响讨论结果。
推论 2[5]由式(2)定义的 Ding-Helleseth-Lam序列(su)的线性复杂度为
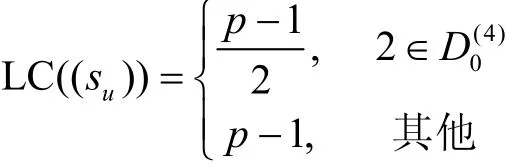
对于 Hall六次剩余序列,由于p=4x2+ 2 7,则有p≡-1(m o d 8)或p≡ 3(mod 8)。
此外,若p≡-1(m o d 8),那么由[6, Lemma 2],可 知和中有一个值为1,其他2个值为0,其中β是F2的某一个扩域的p阶本原单位根。由[6,Theorem 1], 存 在 β 使 得对同一个β,由[6, Theorem 1]的证明可得式(9)。

若p≡ 3(mod 8) ,类似地,由[6, Lemma 1],可 知和而其他2个值为其中i=0,1,2。注意到
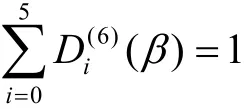
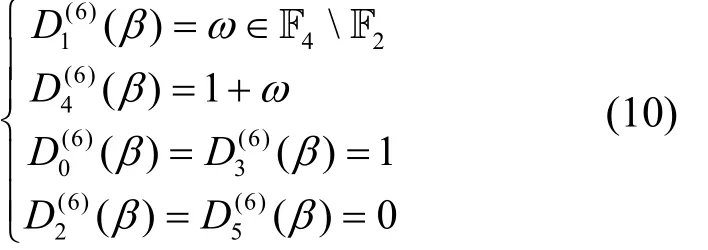
则由引理1,可得命题4。
命题 4设β是F2的某个扩域上的p阶本原单位根,且当p≡-1(mod8)时,β满足式(9);而当p≡ 3(mod 8) 时, β满足式(10),则由式(3)定义的Hall六次剩余序列(su)对应于β的Mattson-Solomon多项式如下所示。
若p≡-1(m o d 8),则
若p≡ 3(mod8),则
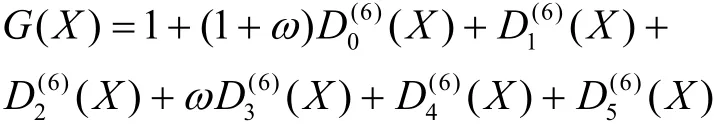
推论 3[6]由式(3)定义的 Hall六次剩余序列(su) 的线性复杂度为
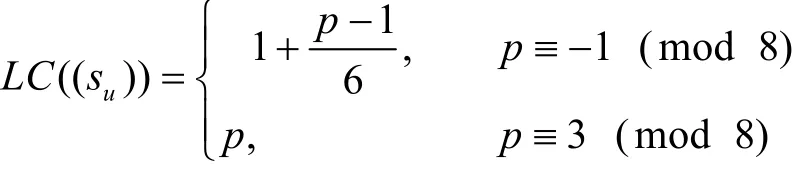
3 k-错线性复杂度
由式(5)可知,周期为p的二元序列(su)的k-错线性复杂度是指在改变序列(su)的第一个周期中至多k项后(随后的其他周期中做相同改变),可得序列()的最小线性复杂度,即
其中,(eu)为一个错误序列满足WH((eu)) ≤k。受到文献[33-34]的启发,下面给出使用(eu)的离散傅里叶变换求序列的k-错线性复杂度的方法。
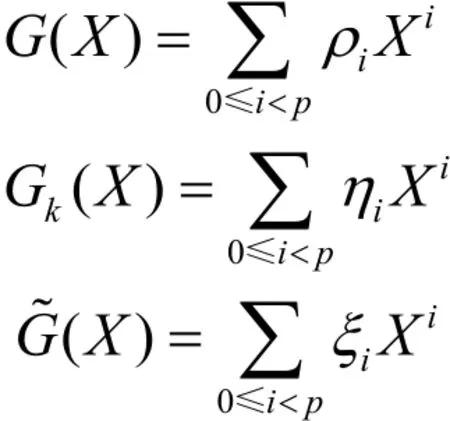
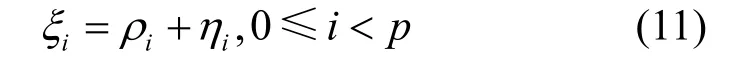
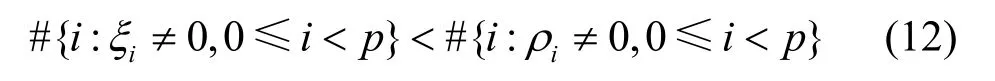
由此证明,序列(su)在改变若干项之后其线性复杂度降低了。
3.1 1-错线性复杂度
命题 5由式(1)定义的 Legendre序列(su) 在F2上的1-错线性复杂度如下
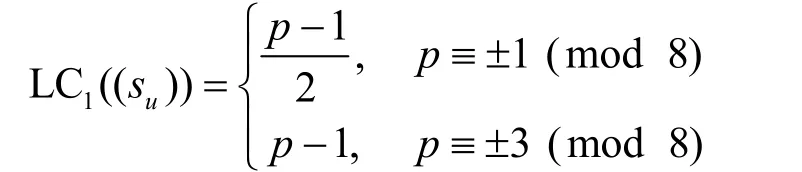
证明不妨设错误序列(eu)的第一个周期中对某个 0 ≤u0<p满足eu0=1 ,而对其他0≤u≠u0<p满足eu= 0 。(eu)的离散傅里叶变换为η=βiu0,0≤i<p。特别地,若u=0,则对所有0的 0≤i<p有 ηi=1;否则,η0=1且对所有的1≤i<p有ηi的阶为p。
下面考虑p≡-1(m o d 8)的情况。由命题 2和式(11),可得

若u0≠0,则对所有的1≤i<p有 ξi≠0,且修改后的序列的线性复杂度满足而当u0=0时,有
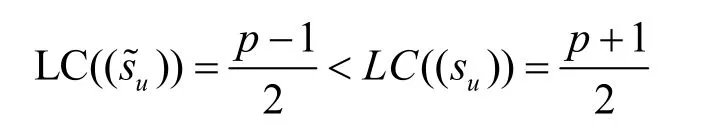
这说明若改变序列(su)的第一项s0的值后,其线性复杂度从这就证明了第一种情况,而对于其他3种情况的证明方法类似。
证毕。
用命题5的证明方法,可以得到下面2个结论。
命题 6由式(2)定义的 Ding-Helleseth-Lam 序列(su)在F2上的1-错线性复杂度为

命题7由式(3)定义的Hall六次剩余序列(su)在F2上的1-错线性复杂度为
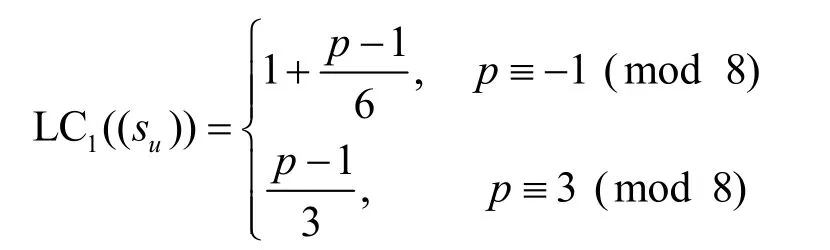
3.2 k-错线性复杂度: 几个特殊情况
对于k≥2的情况,要确定 Legendre序列、Ding-Helleseth-Lam序列和Hall六次剩余序列的k-错线性复杂度是不容易的。但是,在一些特定的条件下可以得到部分结果。通过错误序列(eu)的离散傅里叶变换(η0, η1, … ,ηp-1) 的适当取值,并通过式(11)使得式(13)成立。
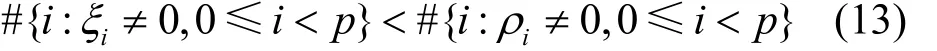
也就是说,改变序列(su) 的WH((eu)) 项可使其线性复杂度降低。然后,从(η0,η1,…,ηp-1) 中计算得到(eu) ,从而得到WH((eu)) ,即k的值。

其中g为第1节中定义的模p的本原元。令
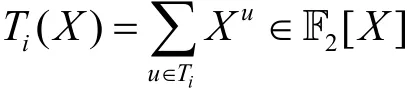
设ℓi表示集合Ti中的最小元素值(也称为陪集首元),其中0≤i<d。对于一个二元序列的离散傅里叶变换为并定 义的 DFT-leader-vector为
由上述T0的定义易知,DFT-leader-vector是由唯一确定的,反之亦然。具体地,若
当p≡-3(mod 8)时,
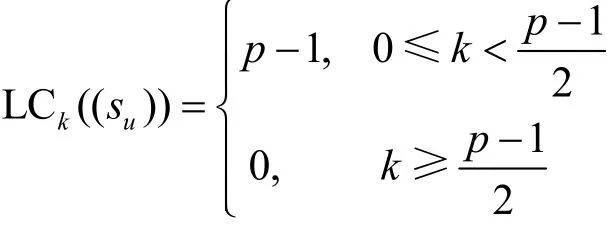
当p≡ 3(mod8)时,
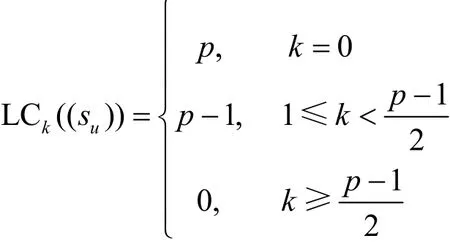
命题8设,则由式(1)定义的Legendre序列在F2上的k-错线性复杂度如下。
当p≡ 1(mod8)时,
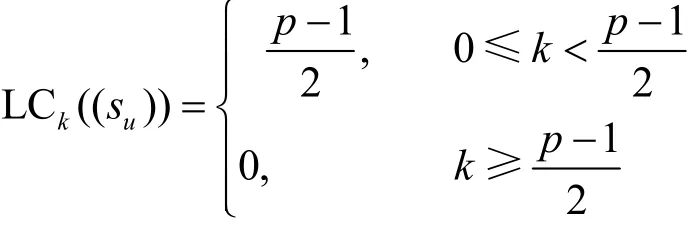
当p≡-1(mod8)时,
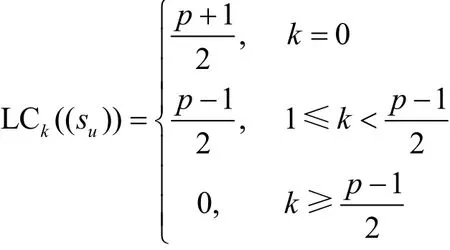
证明由于2是模p的平方剩余,因此,p≡ 1(mod 8)或p≡-1(mod8)。那么,由推论1、命题1和命题5即得所要结果。
命题 9设则由式(1)定义的Legendre序列在F2上的k-错线性复杂度如下
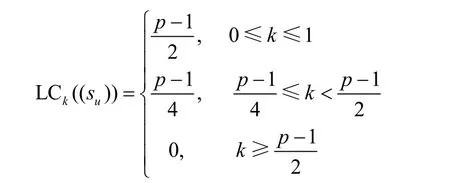
或
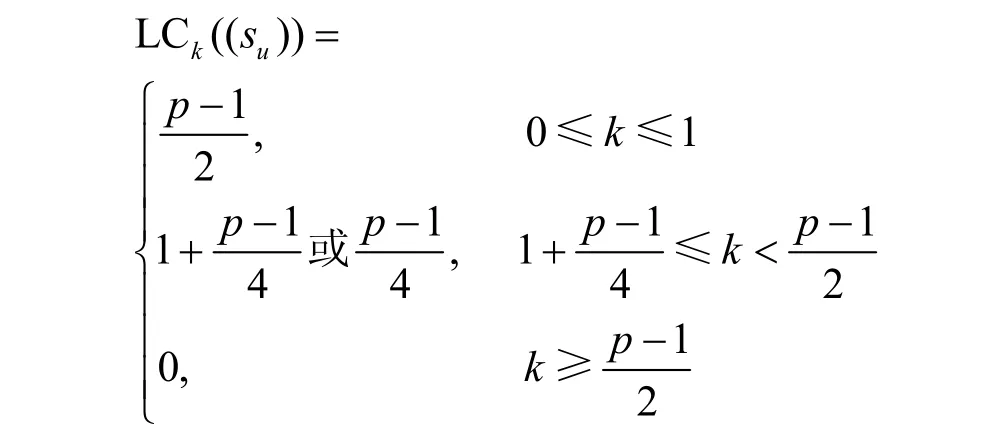
证明由另外,根据上述定义的Ti,有由命题2中假设的或
再由命题 2,序列(su)的离散傅里叶变换(ρ0,ρ1,… ,ρp-1) 的DFT-leader-vector是[0;1,0,1,0]。为了使(su)的k-错线性复杂度降低,即使序列的离散傅里叶变换满足

由式(11)可知,错误序列(eu)的离散傅里叶变换有以下几种情况。
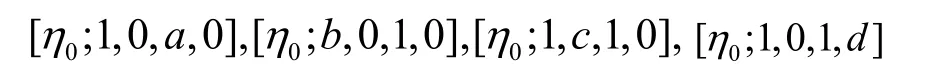
取序列(eu) 的离散傅里叶变换的 DFT-leader-vector 为[η0;1 ,1,1,0],序列(su) 的线性复杂度从降低为则可通过如下计算得到(eu) 。

若命题2中选择的β满足T0(β)=T2(β)=1,则设η0=0 。由于则有或T1(β)=1且T3(β)= 0 。可得
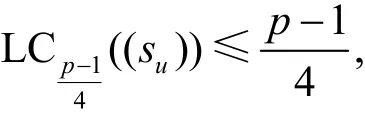
由此完成了第一种情况的证明。
若命题2中选择的β满足T0(β)=T2(β)= 0 ,选择η0=1,则可计算得到满足的错误序列(eu),进而有由命题1可完成第二种情况的证明。
证毕。
下面考虑由式(2)定义的Ding-Helleseth-Lam序列(su) 。若ordp(2)=p-1 ,则有由推论2、命题1和命题3可得
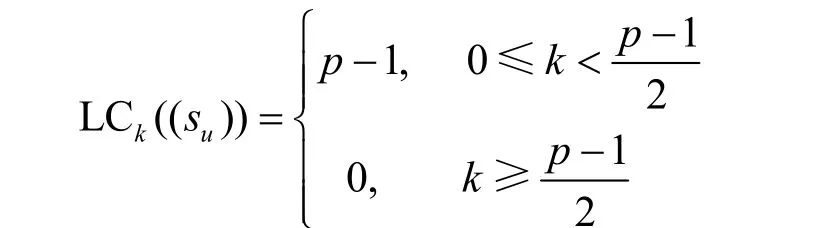
命题10设由式(2)定义的Ding-Helleseth-Lam序列(su)在F2上的k-错线性复杂度为

或
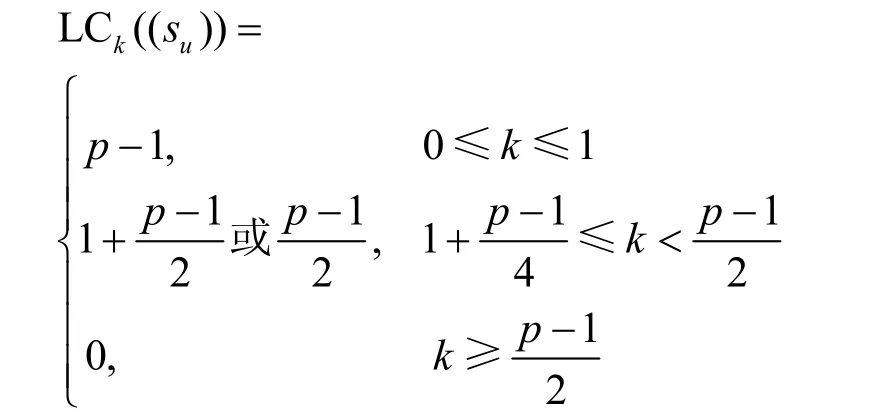
证明由命题3可知,(su)的离散傅里叶变换为

取(eu) 的离散傅里叶变换(η0, η1,… ,ηp-1) 为
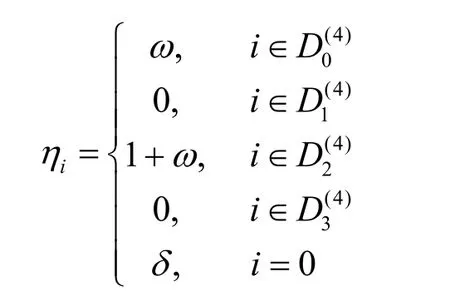
其中,δ ∈F2。通过如下方式计算得到(eu) 。
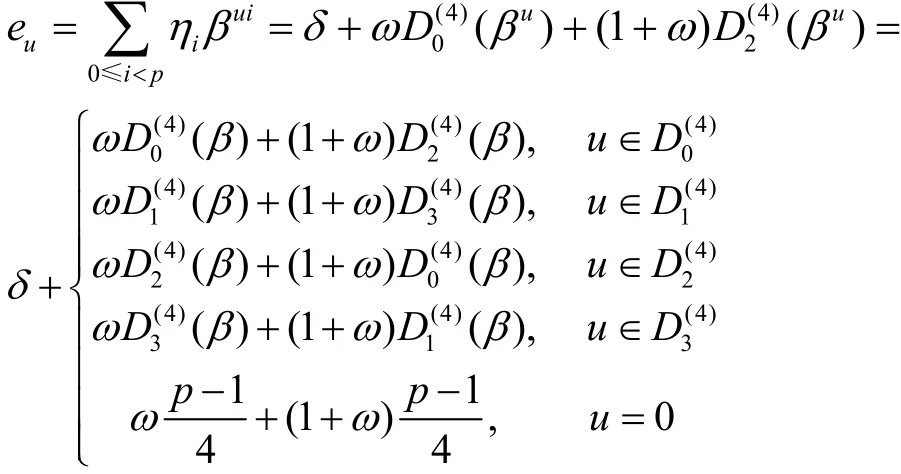
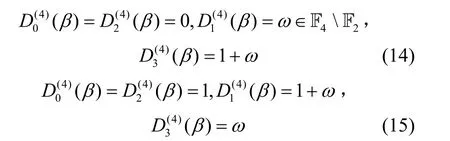
若命题3中选择的β满足式(13),则选择η0=1和再由命题1即可完成第二种情况的证明。证毕。
命题11设则由式(2)定义的Ding-Helleseth-Lam序列(su)在F2上的k-错线性复杂度为
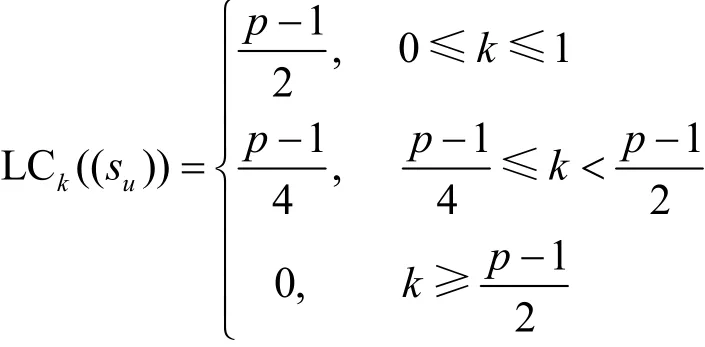
或

证明由于则有且其中0≤i<4。容易验证每个T(β)∈F且在命题 3的假设下,若则式(16)或式(17)成立。
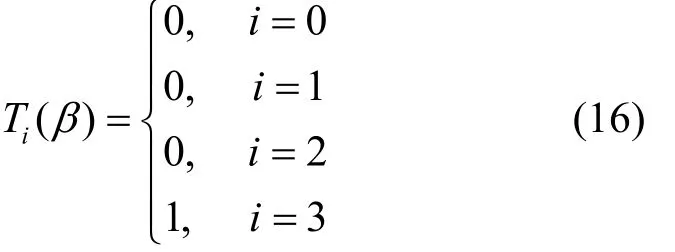

再由命题3可知,(su)的DFT-leader-vector为[0;0,0,1,1]。仿照命题9的证明,通过式(16)选择错误 序 列(eu) 的离 散 傅里叶 变 换(η0,η1,… ,ηp-1) 的DFT-leader-vector为[0;0,0,1,0],或通过式(17)则选为[1;0,0,1,0]。 通过类似的计算,即得所要证明的结果。
证毕。
最后,考虑由式(3)定义的 Hall六次剩余序列(su) 的k-错线性复杂度。由[6, Lemma 1]知,当因 此 , 当p≡-1(mod 8) 时 ,下面分析ord(2)取最大的情况。
命题 12由式(3)定义的Hall六次剩余序列(su)在F2上的k-错线性复杂度如下。
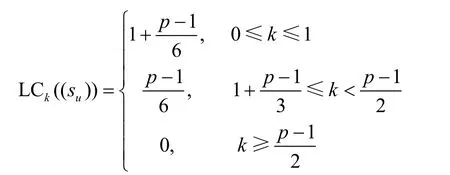
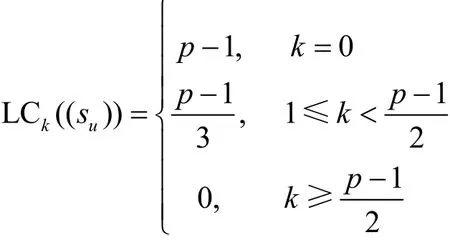
证明当p≡-1(m o d 8)时,由命题 4可知,(su) 的 离 散 傅 里 叶 变 换(ρ0,ρ1, … ,ρp-1) 的DFT-leader-vector为[1;0,0,0,1,0,0]。选择错误序列(eu) 的离 散 傅 里 叶 变 换(η0,η1,… ,ηp-1) 的DFT-leadervector为[1;0,0,1,1,0,0],则可计算得出eu。
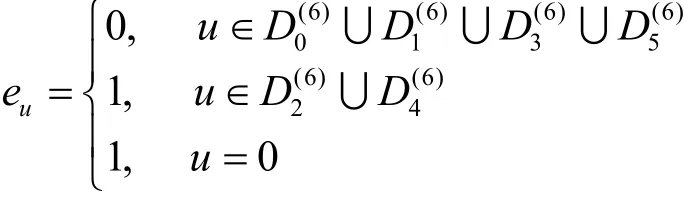
因此,可以找到一个错误序列(eu)满足使得序列(s)的线性复杂度从u从而完成了第一种情况的证明。而对于第二种情况,则由命题4和命题1即得。
证毕。
4 结束语
本文分别利用 Legendre序列、Ding-Helleseth-Lam序列和Hall六次剩余序列的离散傅里叶变换确定这些序列的1-错线性复杂度,并在特定条件下得到这些序列的k-错线性复杂度的部分结果,其中k>1且d为小的正整数。
认为考虑一般的ordp(2)和适当大的k的情况是一个具有挑战性的工作。若错误序列(eu)的满足a0∈F2且对其他那么(eu) 可通过如式(18)所示的迹函数的和计算得到。