基于小区间干扰消除的NB-IoT时延估计算法

唐宏，牟泓彦，杨浩澜

（1. 重庆邮电大学通信与信息工程学院，重庆 400065；2. 重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065）

1 引言

在3GPP R14标准中提出的窄带物联网（NB-IoT，narrow band internet of things）支持以下几种基站定位方式：全球辅助定位卫星系统（A-GNSS，assisted global navigation satellite system）、E-CID（E-UTRAN cell identifier）、基于观测到达时间差（OTDOA，observed time difference of arrival）的下行链路定位方法或基于观测到达时间差（UTDOA，uplink-time difference of arrival）的上行链路定位方法[1]。综合考虑终端复杂度、网络容量、成本和资源及定位场景，如果对OTDOA定位方式做相应的适应性改进，可以使其相对于其他定位方式更具有普适性，更能切合海量 NB-IoT节点的定位成本需求。基于OTDOA的定位方式主要是通过测量3个及以上小区定位参考信号（PRS，positioning reference signal）到达定位终端的时延估计（TDE，time delay estimation）值，并在已知各基站位置的情况下估计出终端的位置，故时延估计在基于OTDOA的NB-IoT定位中是非常重要的一个影响因素。

经典时延估计算法的代表是互相关法[2]，它通过搜索本地 PRS信号与接收信号的相关峰值来估计信号时延，其优势在于算法简单、复杂度低，非常符合NB-IoT的低功耗、低成本的要求，但时延估计精度受到系统采样率的影响严重，使并不适用于低采样率（即1.92 MHz）的NB-IoT设备的精确定位。超分辨率的时延估计算法[3-5]由于复杂度问题而使物联网设备的成本提高，并影响到其功耗。另外，由于建筑物以及地形的原因，导致移动通信信道结构复杂，不同小区发送的PRS信号通过多条路径到达定位终端，在此过程中小区间的信号相互干扰，小区内的信号由于多径效应也会受到非视距（NLOS，non-light of sight）影响[6]，这些因素都会导致时延估计误差甚至产生明显的错误。不少学者提出了一些抑制NLOS影响和消除小区间干扰的算法[7-9]，但这些算法大多比较复杂，如文献[9]中提到的基于期望最大化的连续干扰消除（EM-SIC,expectation-maximization based successive interference cancellation）算法，该算法会导致比较大的系统开销。现有的一些基于互相关的时延估计算法[10-12]虽然在精度上有一定提升，但却未能系统地考虑小区间信号干扰以及NLOS影响。

针对上述问题并结合3GPP R14标准，本文提出了一种基于小区间干扰消除的时延估计算法。一方面，该算法将服务基站和邻近基站的时延估计分开处理，先重建来自服务基站的接收信号，在此基础上消除服务基站信号的强干扰，再利用迭代连续干扰消除算法逐步去除接收到的来自邻近基站信号之间的相互干扰。另一方面，为了突破低采样率的限制，该算法在传统相关算法的基础上提出一种时频互相关交叠的时延估计算法（F&T_TDE，time delay estimation algorithm based on frequency-time overlapping cross-correlation），主要包括以下2个阶段：第一阶段，联合多个OFDM符号利用相关算法得到初步的时延估计值，并采用基于噪声门限的首达径搜索算法来抑制多径效应的影响；第二阶段，选出部分接收信号进行插值处理，得到精确的时延估计值。此外，考虑到工程实现中的极端条件下，可能存在定位基站不足3个的情况，导致本文所提算法无法估计出终端设备的位置，此时需要加入一个辅助定位算法来应对此类情形。常见的非基站定位的算法有GPS定位、锚节点定位、指纹定位等方法，综合考虑NB-IoT低功耗、低成本的特点、定位总成本等方面的因素，引入锚节点定位更加切合实际应用场景。最后通过仿真分析了时延估计算法的几个常用的性能指标以及辅助定位的性能，验证了所提算法的可行性。

2 基于NB-IoT系统的信号处理模型

根据3GPP协议[1]，PRS信号应在NPRS个连续定位子帧中传输，其中NPRS由高层协议配置，参照3GPP协议中关于 PRS的产生原理，可得当lN≤n＜（l+ 1）N时，时域PRS信号为

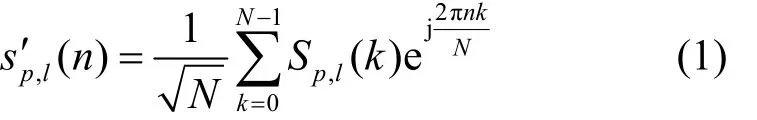
其中，p=0表示信号来自服务基站，p=1,…,P-1（P表示参与定位的基站个数）表示信号来自不同的邻近基站；一个无线子帧有2个时隙，一个时隙包括7个OFDM符号，则一个定位子帧的OFDM符号数L=14，l∈{0,1,2,…,L-1}；N表示快速傅里叶逆变换（IFFT, inverse fanst Fourier transform）的长度；Sp,l（k）为经过资源映射后第p个基站第l个OFDM符号对应的频域PRS信号；加上长度为NCP的保护间隔后，对应的时域发送 PRS信号表示为sp,l（n）。发送的信号经过M条路径到达接收端，则在NB-IoT设备终端对应的第l个OFDM符号在路径m的时域接收信号为

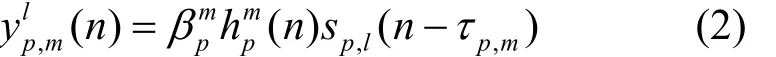
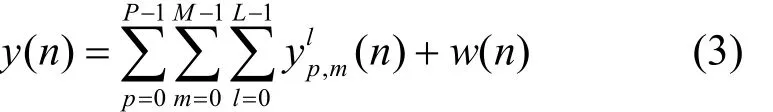
用rp,l（n）表示信号sp,l（n）与y（n）的互相关函数，如式（4）所示。

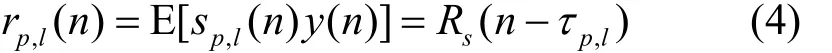
由自相关函数的 Hermit性质及原点达最大值的特性[13]，即

由式（5）可知，当n=τp,l时，rp,l（n）取最大值，减去初始延迟数τp,init，最后得到时延估计值tˆp,l如式（6）所示。

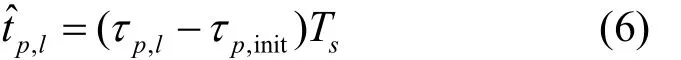
其中，Ts表示采样点的时间间隔。

3 基于小区间干扰消除的NB-IoT时延估计算法描述

由式（2）～式（5）可知，在时延估计过程中，主要面临以下3个问题：1）其他基站发送信号的干扰；2）自身多径效应导致的NLOS的影响；3）NB-IoT具有低采样速率，严重影响了传统的相关时延估计算法的精度。针对以上问题，引入小区间干扰消除算法（I_SIC），多次迭代消除信号之间的相互干扰，在每一次迭代中利用F&T_TDE算法估算出时延估计值，迭代结束时选出最优的时延估计值代入定位解算法中估算出终端的位置坐标。除了以上3个问题之外，在现实环境中可能会存在因定位基站数不足3个的情况导致算法失效，于是在3.4节给出补充算法以应对该特殊情景。当基站数大于3时采用主体时延估计算法，并用Chan算法[14]进行定位解算；否则使用辅助定位算法。本文总体思路及主体基于小区间干扰消除的NB-IoT时延估计算法架构如图1所示。

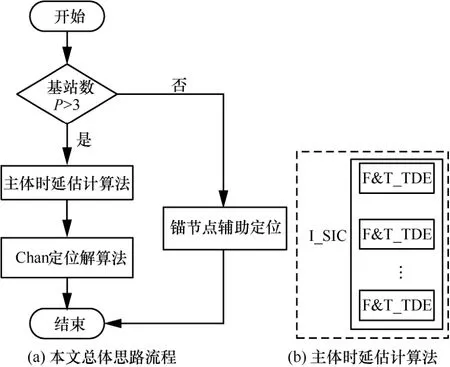
图1 总体思路流程及主体时延估计算法架构

3.1 I_SIC算法及主体时延估计算法流程

小区参考信号（CRS，cell-specific reference signal）持续不断发送，由服务基站发送的 CRS信号受到其他基站信号的干扰较小，因此在接收PRS信号之前利用CRS信号对服务基站与用户终端进行信道估计[15]。处理各基站到终端的时延估计值方法如下：首先，利用 CRS信号估计服务基站与终端之间的信道状态；其次，在接收端接收来自各基站的PRS信号，并利用已有的服务基站与终端之间的信道状态在接收端重构服务小区的PRS信号，利用F&T_TDE算法对服务基站进行时延估计；最后，从总的接收PRS信号中减去重构的来自服务基站的 PRS信号以消除其对邻近基站时延估计的影响，在此基础之上采用连续迭代干扰消除算法逐步消除邻近小区之间信号干扰的影响，同时利用F&T_TDE算法对服务基站进行时延估计，经过多次迭代干扰消除，选择出最佳时延估计值。主体时延估计算法的流程伪代码如算法1所示，其中，y（n）表示设备终端总的接收信号，（n）和分别表示经过q次迭代处理后第p个小区的时域接收信号及时延估计值，tp表示第p个小区最终得到的时延估计值，Ni为干扰消除迭代次数。

算法1主体时延估计算法

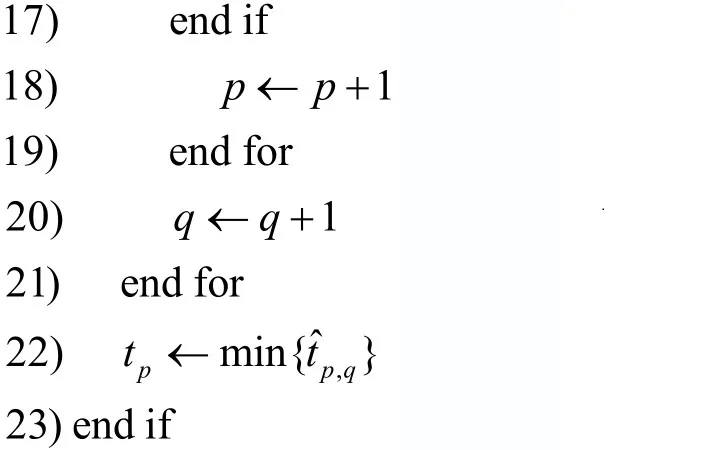
3.2 F&T_TDE算法

小区间干扰消除只能在一定程度上抑制其他小区的干扰信号，并不能解决NB-IoT系统采样率低的问题。想要大幅度提高时延估计精度，需要改进时延估计算法。为了改善串行干扰避免产生误差传播，在进行时延估计之前，先基于发送的PRS信号按其能量从大到小对各邻近基站到终端的时延估计顺序进行排序，接下来通过2个阶段逐步提升时延估计精度。

3.2.1 时延值粗估计阶段

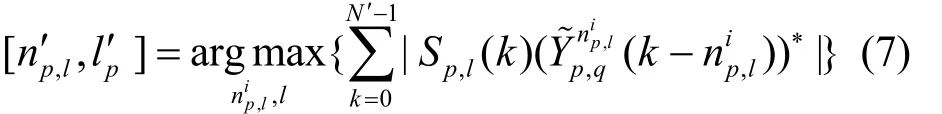
其中，当p=0时，q=1，p＞0时，q∈{1,2,…,Ni}；Ni表示连续干扰消除算法迭代的总次数。即为第q次迭代粗估计值延迟数。

由于噪声以及多径效应会导致NLOS影响，此时得到的时延值存在较大误差，因此本文采用首达径搜索算法来减小误差。算法具体实现过程如下。

在信号到来之前，接收端先采集噪声信号并转换成频域信号Wϕ（k），将其与本地PRS信号做频域相关，重复Φ次，得到如式（8）所示的平均值（即底噪均值）。

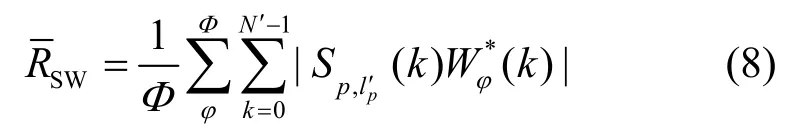
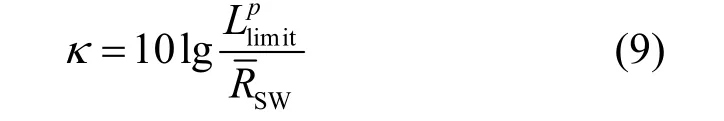
将时延值粗估计得到的具有最大峰值的OFDM符号l′p对应的频域接收信号与本地PRS信号进行频域相关，得到相关函数其中

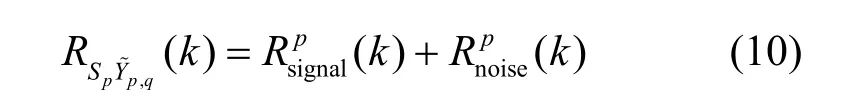
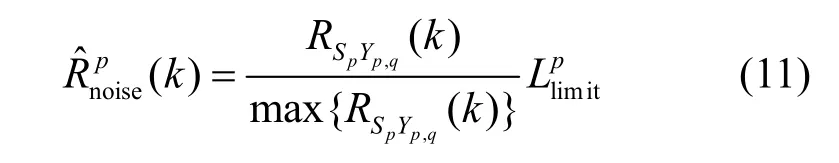
当首达径信号的幅值较小时，有用信号会被噪声及干扰信号所淹没，无法根据首达径时延值来确定最终所需的时延估计值。故设定一个幅度门限α，当首达径的幅度小于该门限时，将选择一条次优径，即时延值仅大于首达径的路径，由此可得首达径搜索式如式（12）所示。

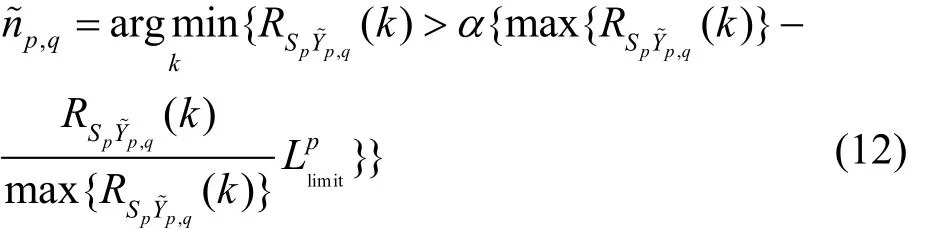
利用MATLAB仿真软件，针对不同的α值，仿真得到时延估计值的概率密度函数（PDF, probability density function）分布如图2所示。当α=0.2时，首达径的时延估计值会受到噪声严重的干扰，过早产生误判；当α=0.8时，若首达径幅度偏小，则易错过判决。在本文后面的仿真中，取α=0.4，得到了比较理想的效果。

3.2.2 时延值精估计阶段

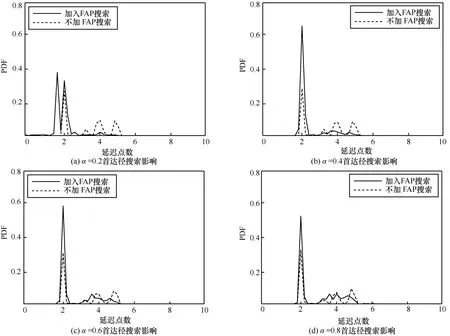
图2 不同的α对FAP搜索的影响分析

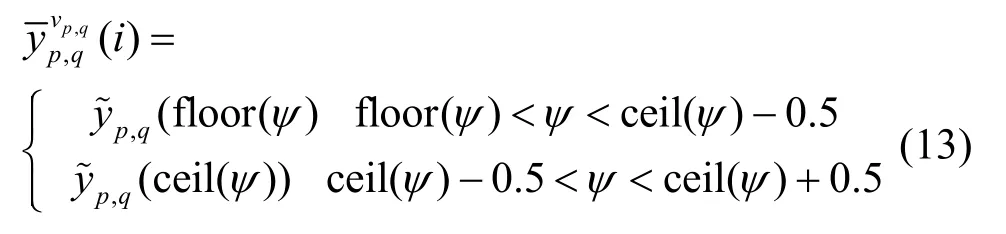
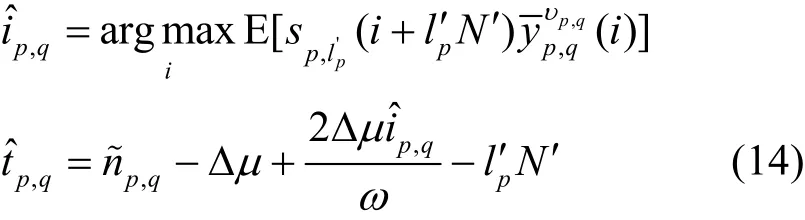
利用3.3节所述的信道估计算法得到基站p与终端之间的信道状态，并重建出接收到的来自该基站的信号，在接收信号）中减去该重建信号得到式（15）与式（16）。

若p＜P-1，则有

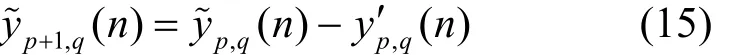
若p=P-1且q≤Ni，则有?

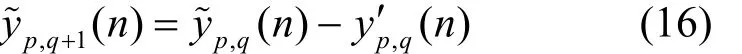
3.3 信道估计

为了降低算法的计算复杂度，本文采用最小二乘法对基站p到用户终端的定位参考信号进行信道估计。当p=0时，对服务基站的CRS信号进行信道估计，得到系统函数如式（17）所示。

其中，YCRS、SCRS,l分别表示终端接收的CRS信号和服务基站发送的CRS信号。对该系统函数进行线性插值[16]得到PRS信号时频位置的信道估计，并对其进行 IFFT变换可得h0,1（i+lN′），其中i=0 ,1,2,… ,N′-1。重建后的来自服务基站的信号为

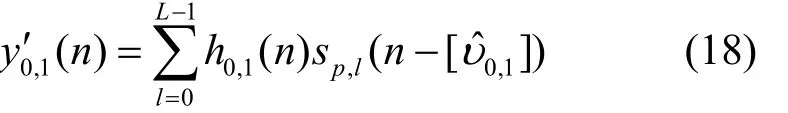
其中，n∈ [lN′,（l+1）N′]。

此时，p＞0，得到系统函数如式（19）所示。

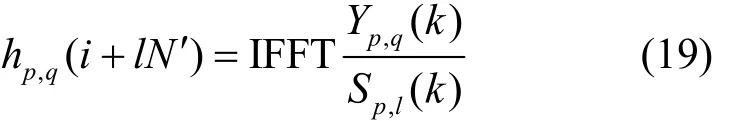
根据式（19）所示的系统函数对接收到的来自基站p的信号进行信号重建，重建后的信号为

其中，n∈ [lN′,（l+1）N′]，[⋅]表示取整。

3.4 锚节点定位算法

DV-Hop定位算法是锚节点定位的关键技术之一，其采取距离矢量-跳数机制，不需要测量节点间距，也不需要附加硬件支持，是一种备受关注的距离无关的（range-free）算法。本文选择 DV-Hop算法作为辅助定位算法。对于基站部署较少的区域，当基站数不足4（基站数为3时的位置估计偏差比较大）时，终端设备节点向锚节点广播一个定位数据分组，锚节点记录接收该数据分组的接收时间戳和待定位终端节点的ID。同时，锚节点之间通过卫星导航进行时间同步并获得终端设备节点地理位置数据存储至后台服务器，为算法处理提供相关参数。各锚节点向网关发送一个新的数据分组，网关将这个新的数据分组转发给后台服务器，利用加权质心算法估计终端节点的位置坐标[17]。需要说明的是，锚节点定位算法作为本文所提算法的一个辅助部分，只有在主体算法失效时才发挥作用。

4 仿真结果

4.1 仿真参数设置

仿真时，由于同步网络模式，所有基站发送的无线子帧在时域上是对齐的。由于NB-IoT网络主要面向宏观、低速的物体，故仿真中假设设备终端移动速度为0 km/s，其他仿真参数根据 3GPP R14中对PRS信号以及基于OTDOA定位方式规定设置[18]，具体参数设置如表1所示。网络部署如图3（a）所示，随机选取撒落在深灰色区域的NB-IoT设备终端节点（实心节点），在每个500m×500m区域内以网格状固定放置m个锚节点（图 3（a）中空心节点），并配置GNSS定位模块作为定位的参考节点，当参与定位的基站数不足4个时启用锚节点定位。当研究距离对时延估计的影响时，则选取如图3（b）方向1区域的设备终端。另外，选择离终端最近的4个基站作为定位基站，其中基站 0（位于服务小区的中心）为服务基站，基站1/2/3（位于邻近小区1/2/3的中心）为邻近基站。

表1 实验仿真参数

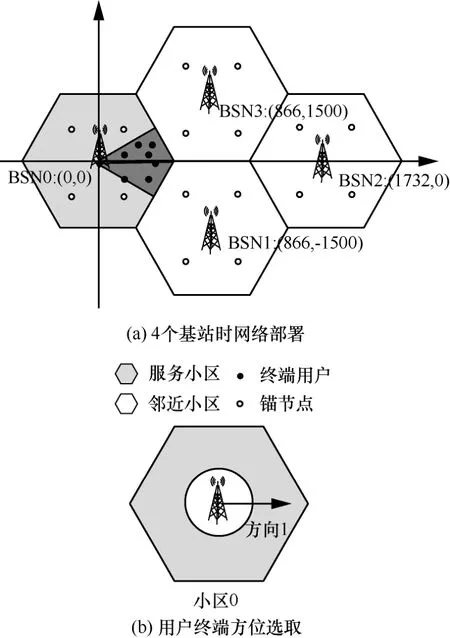
图3 网络部署

在仿真中，针对基于定位参考信号的时延估计主要采用时延估计值的检测概率（PD，probability of detection）、时延估计的均方根误差（RMSE，root mean square error）和设备终端定位的误差累积分布函数（CDF，cumulative distribution function）来衡量定位效果，针对基于锚节点的辅助定位主要采用定位误差来衡量。

4.2 仿真结果分析

4.2.1 检测概率

本文中检测概率是指，在M次蒙特卡洛仿真实验中，时延估计值在给定的某一可接受的门限值Tthreshold内的概率。为了满足参与定位的用户位于服务基站覆盖范围内，此处门限值即时延误差小于相邻两基站信号传播的时间。在图4中，蒙特卡洛仿真次数设置为1 000，分别给出服务小区和邻近小区1检测概率PD随SNR变化的情况。由图4（a）可知，当SNR大于20 dB时，检测概率呈明显的上升趋势；当SNR小于-12 dB时，由于噪声的影响，所提算法以及2种对比算法得到的服务小区检测概率非常低，而且所提算法在信噪比过低的情况下，重建信号误差太大，严重影响时延估计，检测概率低于EM-SIC算法；当SNR大于-12 dB时，检测概率将超过EM-SIC算法；此外，所提算法相对于另外2种算法，检测概率曲线上升趋势更加显著。同理，由图 4（b）可知，对于邻近小区 1（邻近小区2/3与1的曲线走势基本一致），当SNR大于-20 dB时，随着SNR的增加，检测概率呈现出明显的上升趋势，而所提算法的检测概率相对 EM-SIC算法和传统算法更高；为了凸显小区间干扰消除的效果，图 4（b）中同时给出未加干扰消除的情况，可以看出，加入干扰消除可以有效提升检测概率。

4.2.2 均方根误差曲线

均方根误差的定义如式（21）所示。

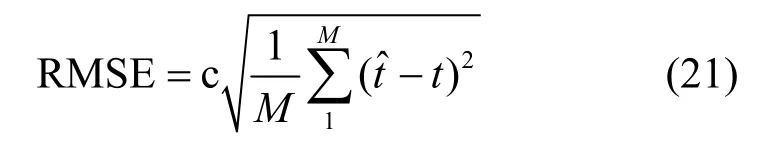
其中，c为光速，取值为 3 .0× 108m/s；M为蒙特卡洛仿真次数，取值为1 000；t为实际的时延值。另外，克拉美罗下界（CRLB，Cramer-Rao lower bound）为时延估计的误差提供了一个衡量的标准，由文献[19]可知，在AWGN环境下NB-IoT时延估计的CRLB下界可以表示为

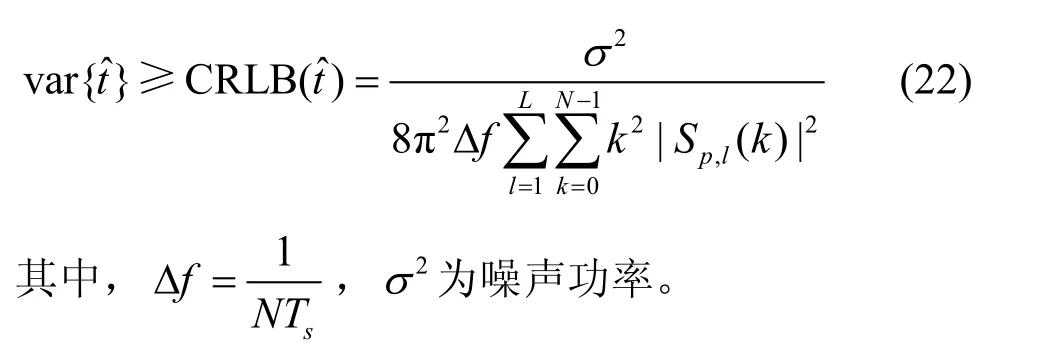
时延估计均方误差可以用来衡量时延估计的准确性。图5（a）对服务小区时延估计的均方误差进行了对比，由于所提算法利用对小区参考信号进行信道估计重建服务小区定位参考信号，得到的时延估计值明显比传统相关算法和EM-SIC算法更接近CRLB下界。图5（b）对邻近小区时延估计的均方误差进行了对比，由图5（b）可知，所提算法对邻近小区的信号进行迭代连续干扰消除可以在一定程度上提升时延估计的准确性。

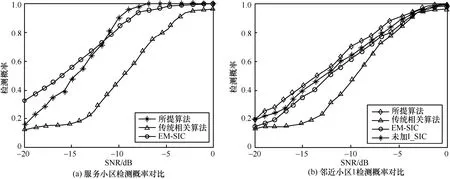
图4 服务小区和邻近小区1检测概率随SNR变化的情况

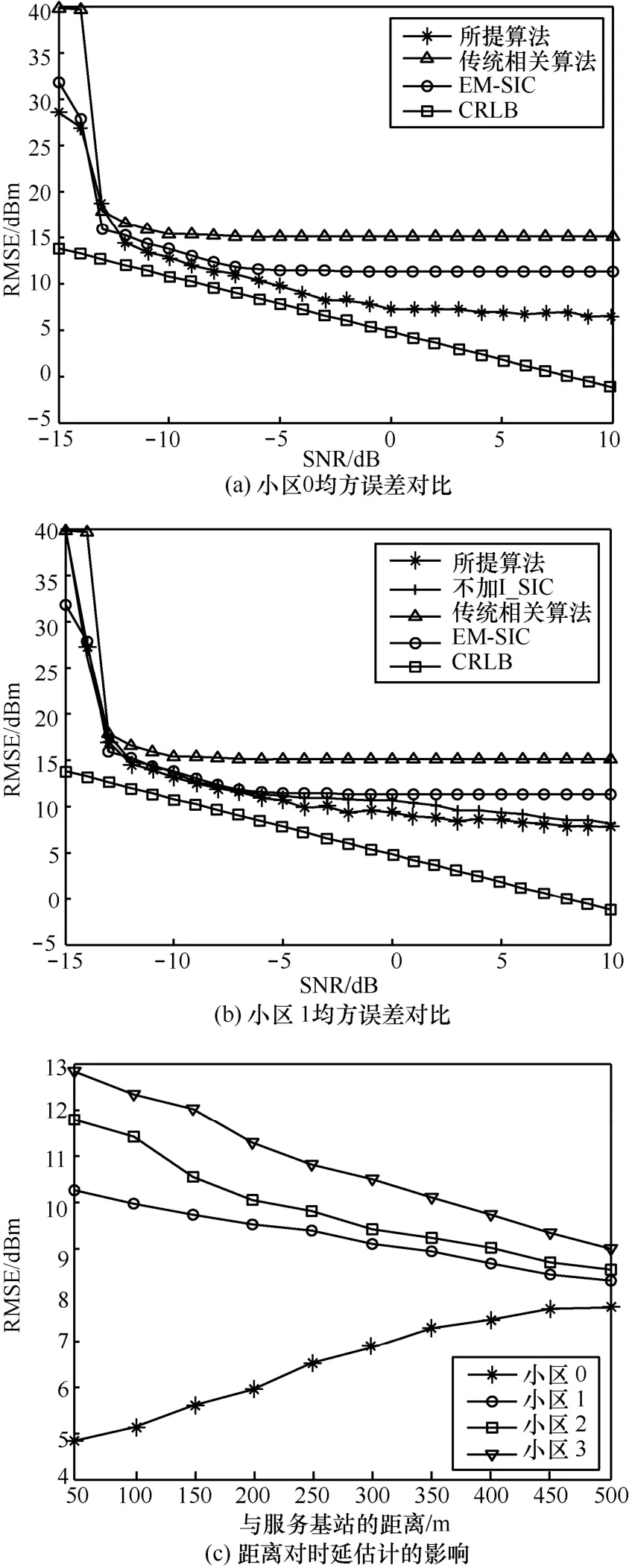
图5 小区 0/1时延估计均方误差变化曲线

除了SNR会影响时延估计结果外，定位终端与服务基站及邻近基站之间的距离也会影响时延估计。在图5（c）中，给出SNR=5时服务基站与定位终端之间的距离（沿着图3（b）中方向1）对时延估计的影响曲线。可以看出，当距离较小的时候，服务小区的均方误差比较小，而邻近小区受到服务小区的影响严重，时延估计均方误差比较大；随着距离的增加，服务小区的均方误差逐渐增加，而邻近小区的均方误差逐渐减小。由此，从距离的对时延估计影响的角度解释了小区间干扰消除的重要性。

4.2.3 定位误差累积分布函数

当定位解算方法确定后，用户终端的定位精度由时延估计的准确性决定，即由多个时延估计值（3个及以上基站到用户终端的时延估计值）共同决定。本文仿真采用 Chan算法来求解，该算法在时延估计误差很小时能达到CRLB下界。

图6所示为传统算法、本文所提算法及EM-SIC算法的定位误差曲线的对比。由图 6可知，本文算法的定位精度明显高于传统算法和 EM-SIC算法，这是由于本文所提算法融入了干扰消除，在一定程度上提升了算法的定位精度。

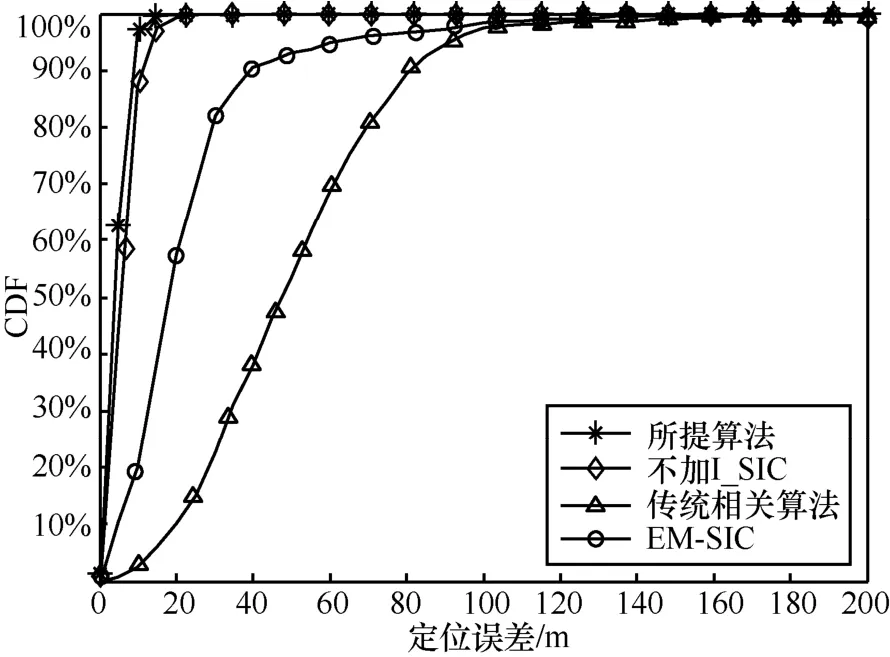
图6 定位误差曲线对比

表2为不同累积误差时，不同算法的定位误差。如表2所示，当累积误差达到50%时，本文算法的定位误差可以达到4.27 m，而此时传统算法定位误差为47.56 m，EM-SIC算法定位误差为18.52 m；当累计误差达到90%时，三者之间的差距更大。

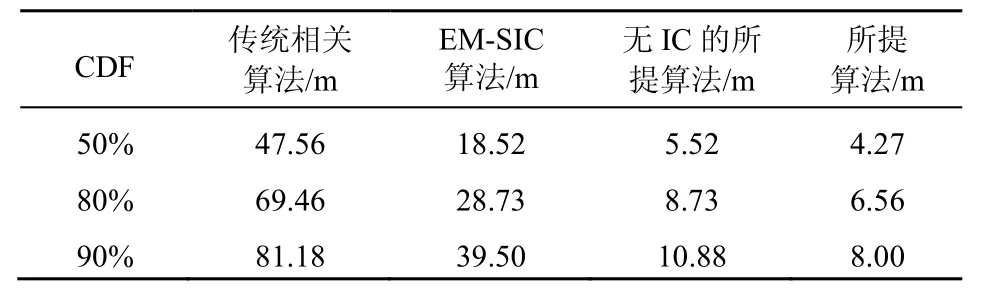
表2 不同累积误差对应的定位误差分析

4.2.4 辅助定位仿真分析

图7所示为锚节点定位误差分析。可以看出，锚节点的个数以及节点的通信半径都会影响定位的精度。当节点的通信半径为60 m时，锚节点数量与定位误差的关系如图 7（a）所示，随着锚节点数量的增加，定位误差逐渐减少，但是同时伴随着定位成本的增加。通信半径和锚节点的密集程度之间也相互制约，当锚节点的位置确定时，节点间的距离也就确定了，通信半径会影响算法的平均跳距，从而影响定位精度，此时定位误差随着通信半径的增加呈先减小后逐渐增大的趋势，转折点的位置由通信半径和锚节点密集程度共同决定。图7（b）为锚节点为64个时，通信半径与定位误差之间的关系。值得注意的是，通信半径的增加是由增加发送功率得到的。

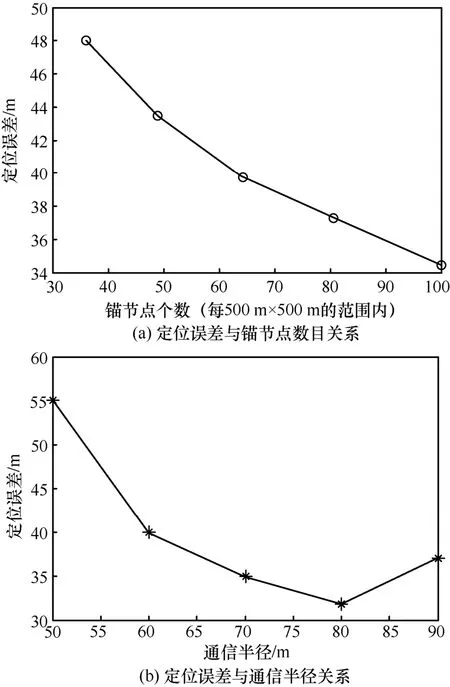
图7 锚节点定位误差分析

通过上述仿真分析可知，要提高辅助定位算法的定位精度，需要增加锚节点的个数和通信半径，此时定位成本也会同比增加，然而该辅助定位算法位置估计的效果远不及本文所提时延估计算法，故该辅助定位算法仅作为真实定位场景中定位基站不足时的备用方案。

5 结束语

本文针对NB-IoT的成本受限、低采样率等问题，提出了一种基于小区间干扰消除的时延估计算法。该算法延续了传统的互相关算法低复杂度的优点，采用基站参与定位以减小设备开销，更加满足 NB-IoT低功耗、低成本的特点。通过仿真分析，所提时延估计算法可以有效地抑制小区间干扰及NLOS的影响，时延估计精度明显高于对比算法，更加切合当今高精度的位置感知需要。至于是否存在SNR小于-20dB的定位场景以及是否有必要改善-20dB以下的TDE精度，还需要进一步的研究。