面向物联网无线携能通信系统的机会安全传输方案
2019-03-13马克明陈亚军胡鑫黄开枝季新生
马克明,陈亚军,胡鑫,黄开枝,季新生
(国家数字交换系统工程技术研究中心,河南 郑州 450002)
1 引言
物联网作为未来5G的核心技术之一,具有广阔的应用前景。为便于大规模灵活部署,物联网设备一般采用电池供电,而有限的电池容量从根本上制约着整个网络的工作寿命,因此如何延长电源的工作寿命以降低维护成本成为物联网应用中亟需解决的问题之一。无线携能通信(SWIPT, simultaneous wireless information and power transfer)[1-3],作为无线通信技术与无线输电技术交叉融合的前沿方向,利用无线电信号的广播特性实现了信息与能量的并行传输,能够为能量受限用户提供稳定而持续的电源供应。但同时,无线信道的开放性也导致 SWIPT系统中用户信息泄露的问题难以避免,如何保证其安全通信成为业界的研究热点之一。作为传统加密手段的补充手段,物理层安全技术[4-7]能够利用无线信道的“指纹特性”,以较低的计算复杂度保证合法通信信息不被窃听,为解决SWIPT信息泄露问题提供了新的思路。
根据接收端工作原理的不同,SWIPT系统可分为时域切换(TS, time switching)型和功率分裂(PS,power splitter)型[3],其中TS型SWIPT(后文简称TS-SWIPT)系统由于实现复杂度较低,受到了业界的广泛关注,本文主要针对该类型系统中的物理层安全问题展开研究。文献[8]考虑了一个单天线信息接收机(IR, information receiver)和多个单天线能量接收机(ER, energy receiver)的场景,将ER视作潜在窃听者,并通过优化设计发射波束,在满足ER能量约束的同时保证IR不受窃听。文献[9-10]针对上述场景中多个ER联合窃听IR时的安全传输方案进行了研究。在此基础上,文献[11]针对IR与ER的天线数进行扩展,并通过设计不同的发射波束,设计了ER能量约束下的IR保密速率最大化和IR保密速率约束下的ER能量收益最大化2种方案。文献[12-13]考虑了发送端信道状态信息非理想的情况,并通过设计顽健的发射波束降低估计误差对安全性能的影响。考虑到人工噪声能够在传输能量的同时带来安全增益,文献[14-16]通过引入人工噪声辅助并联合优化发射波束来同时保证ER的能量收益和 IR的通信安全。上述文献均固定分配能量传输与信息传输2种不同阶段的时隙,未充分考虑信道特征在时域上的变化及2种不同阶段的安全需求差异。
针对上述问题,从TS-SWIPT系统中完整的“采集-解码”周期入手,本文提出一种机会安全传输方案。首先,考虑一个随机分布的TS-SWIPT网络,包括多个小区、多个用户与多个窃听者,其中用户以非线性模型转化并储存能量;其次,结合无线信道的时变特性,充分考虑信息传输与能量输送的安全需求差异,提出基于信干噪比门限的“信息-能量”动态切换传输方案,即发送端在每个时隙的初始时刻估计信道,若接收端的信干噪比高于预设门限则向其传输私密信息,否则传输公开信息以完成能量输送;然后,针对所提方案,分析了其输送能量的稳定性和效率,并分别在窃听者独立窃听、联合窃听的场景下分析了传输信息的可靠性和安全性;最后,在能量约束条件下,为兼顾系统安全性和可靠性,设计了保密吞吐量最优的切换门限选择算法。仿真结果表明,相比传统方案,本文方案将保密吞吐量提高34.15%左右。
2 系统模型
考虑由若干资源中心(RC, resource center)、大量能量受限用户(ECU, energy-constraint user)和被动窃听者(PE, passive eavesdropper)组成的携能通信网络。为了延长物联网设备的寿命,RC利用下行链路特定的时隙为物联网设备传输能量。另外,物联网场景中资源中心在下行链路其他时隙内给物联网设备传输控制信令等私密信息,即每个 RC同时向Ψ个 ECU传输能量与信息,PE企图截获RC与 ECU之间的私密信息。假设每个 RC配置根天线,每个ECU和PE均配置为单天线。由于节点部署具有广泛性与随机性,本文借助随机几何工具将3类节点的空间位置模拟为二维平面上的泊松点过程(PPP, poisson point process),RC、ECU和PE的密度分别为rλ、uλ和eλ。
考虑到物联网接收端硬件简单,本文采用复杂度较低的TS型接收机[17]。当用户切换至能量采集(EH,energy harvesting)模式,利用RF-to-DC电路将射频信号携带的能量转换为直流功率储存,但受限于硬件电路损耗与转换效率,输入功率仅以一定比例转换为直流功率。本文以符合实际的非线性模型(NLM,non-liner model)[18]来模拟RF-to-DC电路的能量转换关系,其输出功率Pout与输入功率Pin的关系可表示为

假设本文所有信道同时考虑大尺度、小尺度衰落的影响,其中大尺度衰落采取标准路径损耗模型,小尺度衰落服从瑞利分块衰落。信道向量表示为其中h∈C1×Mr表示小尺度衰落向量(C为复数集),且每根天线对应的信道hn(1≤n≤M)r服从独立、相同的复高斯随机分布;表示通信双方的欧氏距离;α表示路径损耗系数,α>2。
3 问题描述与方案设计
在无线携能通信中,无线信道承载着信息传输(WIT, wireless information transmission)与能量输送(WPT, wireless power transfer)这2种无线传输,而两者的安全需求却不同,WIT需要保证传输信息不被窃听,而WPT仅依托射频信号携带能量而不需要保证其安全性。TS-SWIPT系统通过周期分割方式实现了信息与能量的并行传输。如图 1(a)所示,传统方案中发送端将下行周期Tdl固定地划分为2个连续区间,其中,αTdl用于WPT,(1-α)Tdl用于WIT。但实际场景中,无线信道具有随机性,传统方案无法根据信道质量动态地调整时隙来满足能量传输、信息传输在可靠性与安全性等方面的差异性需求。

图1 传统方案与本文方案示意
如图1(b)所示,针对以上传统方案存在的问题,本文所提方案利用下行周期中信道质量较好的区间(若干时隙)实现信息的安全传输,其余时间用于完成安全需求较低的能量输送。利用接收信干噪比(SINR, signal to interference-plus-noise ratio)作为信道质量的衡量指标。发送端通过引入SINR门限可实现能量输送与信息传输的切换控制,称为基于SINR门限的动态信能切换(DIPS, dynamic information-power switching)传输方案,方案流程如图2所示。RC将每个下行周期划分为m个时隙,并在每个时隙的初始时刻完成信道估计。RC通过回传链路得到不同接入用户在当前时隙内的接收SINR,并将其与预设的切换门限进行比较,从而实时调整传输内容,具体方法如下:若(用户Ui在第n个时隙的 SINR)大于或等于切换门限 γui,则判定当前时隙的信道质量足够保证安全通信,RC向Ui发送保密信号;否则 RC向Ui发送能量信号。

图2 动态信能切换DIPS传输方案流程
本文传输方案打破了传统方案中WIT与WPT的固有分配模式,尽量选择合法信道质量比较好的时隙来传输私密信息,“尽力而为”地增加了合法信道与窃听信道质量的差异性,从而保证物联网无线携能通信系统信息的安全传输。下面对所提方案的性能进行分析。
4 性能分析及复杂度分析
假设 ECU0位于坐标原点,与 ECU0距离最近的RC记作RC0,且RC0以功率Pr发送信息。RC0基于迫零准则的波束成形(ZFBM, zero-forcing beamforming)向 ECU0发送信号,则tn时隙(周期中的第n个时隙)内 ECU0处的接收SINR可表示为

引理1ECU0处接收 SINR的累积分布函数(CDF, cumulative distribution function)[21]表示为

DIPS传输方案中RC0的工作状态与信道质量有关。若以γu表示RC0控制WIT/WPT切换的SINR门限,则可引入如式(4)所示的符号函数表征其工作状态。

符号函数ϒ含义如下。
1)ϒ=0表示RC0工作于WPT,即此时 ECU0的接收质量相对较差,不适合安全传输,RC0向其发送公开信息以完成能量输送。ϒ=0的发生概率即为能量输送概率(PTP, power transfer probability),表示为
2)ϒ=1表示 RC0工作于 WIT,即此时 ECU0的接收质量符合安全传输的要求,RC0向其传输私密信息;ϒ=1的发生概率即为信息传输概率(ITP, information transfer probability),表示为的互补累积分布函数。
下面分别针对能量输送过程与信息传输过程展开分析。
4.1 能量输送
能量输送WPT的稳定性和效率是SWIPT系统的关键指标,本文分别利用能量中断概率(EOP,energy outage probability)和能量利用率(EUR,energy utilization ratio)来衡量系统能量输送的稳定性和效率。如果用户在某个周期内的能量收益Eu低于其完成一周期工作所需的能量Ec,则影响其后续的正常通信过程,此时被定义为能量中断,概率Pr(Eu<Ec)为能量中断概率;EUR是指用户能量收益与 RC输送能量的总功耗之比,表达式为其中T=T p表示平均传能时Pdlpt长(PTD, power transfer duration)。下面将具体推导能量输送的能量中断概率和能量利用率。
4.1.1 能量中断概率EOP
定理1ECU0采集能量低于所需能量Ec的EOP表示为

证明见附录A。
4.1.2 能量利用率EUR
定理2ECU0采集功率的期望可表示为

4.2 信息传输
本文分别利用连接中断概率(COP, connection outage probability)和安全中断概率(SOP, secrecy outage probability)表征信息传输WIT可靠性和安全性[23],下面对其进行详细分析。
对于目标用户,以 COP衡量其接收过程的可靠性,由定理3给出。
定理3ECU0接收信息时的COP可表示为

由式(7)可知,COP与切换门限γu紧密相关。
除目标用户之外,还存在多个 PE企图截获ECU0的私密信息。以PEi为例,其接收 SINR可表示为

如果PE窃听成功,则传输过程发生安全中断,其概率可改写为其中表示PE接收SINR的CDF,表示目标用户 ECU0的接收速率。因此求解SOP的关键在于仅与合法信道有关,可由定理4给出。
定理4ECU0接收信息时的可达遍历速率为

4.2.1 窃听者独立窃听
若PE独立窃听,则接收SINR最大的PE被视作最具威胁的 PE,记为 P Edanger。其接收其CDF可由定理5给出。
定理5PE独立窃听时接收SINR的CDF可表示为
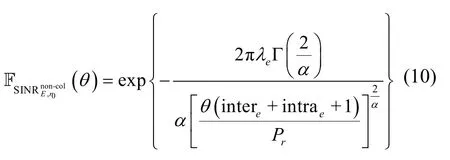
其中,Γ(x)表示 Gamma函数,ϕ表示最短窃听距离(在设置安全保护域[24]的假设下,RC0能够检测到半径为ϕ以内的窃听者,且可通过波束设计阻碍其接收信号),
证明附录B。
4.2.2 窃听者联合窃听
考虑PE联合窃听场景,此时多个单天线PE可等效为一个多天线的窃听者 P Emulti。假设 P Emulti可实现干扰消除[4],则有其CDF可由定理6给出。
定理6PE联合窃听时接收SNR的CDF(α=4)可表示为

证明见附录C。
在此基础上,结合定理3可分别得到2种场景下的平均STP。可将其进一步分解为2个影响因子,即

其中,ASR表示平均可达保密速率(ASR, achievable secrecy rate),ITD 表示平均传信时长(ITD, information transfer duration)。
4.3 性能优化
4.1节和 4.2节的性能分析都在切换门限固定的条件下进行推导。通过分析发现,EOP、EUR及STP等指标与相应阈值(例如Ec、Rc)有关,并且与切换门限γu密切相关。因此,在系统设计时如何选择使系统性能最优的门限值变得尤为重要。
而本文目标是在保证能量输送性能的基础上,提升TS-SWIPT系统的综合性能。为了同时考虑传输的可靠性与安全性,文献[24]提出保密吞吐量(STP, secrecy throughput)的定义,其表达式为ξo=(1-pco)(1-pso)Rs,表示合法用户私密信息安全、可靠地传输的平均速率。在此基础上,结合TS-SWIPT系统的特点,将其定义式拓展为ξ=ξoTI,表征私密信息在单位时间(一个周期)内安全、可靠地传输至目标用户的数据总量,其中TI=Tdlpit表示下行周期中的平均传输时长。
当切换门限值较大时,RC大部分时隙内输送能量,则物联网设备能够采集充分的能量。若此时真实无线环境接收信干噪比大于切换门限值,说明合法信道质量较好,则切换到信息传输模式,此时信息传输的可靠性和安全性都较高;但由于设置的信干噪比门限值较大,RC到物联网设备的下行链路信道质量难以满足传输私密信息的安全性能需求,系统分配给传输信息的时隙较少,那么ξ有可能很小。同理,可分析较小的切换门限值对系统能性能的影响。因此,为使系统性能最优,需优化设计切换门限值。
在优化设计切换门限值时,希望在满足能量约束,并保证可靠性、安全性的条件下,尽量提高系统的综合性能。具体地,以提高表征WIT可靠性和安全性的STP为目标,同时兼顾能量传输的稳定性与效率性、信息传输的可靠性与安全性,则该优化问题可表示为

约束条件为

上述优化问题的求解关键在于各项约束条件下门限取值可行域的确定,首先需对peo、ηeu、pco和pso求导来确定其单调性。对于EOP约束,有

对于EUR约束,由于式(15)分母为常数,只需要考虑分子的单调性,对)求导可得
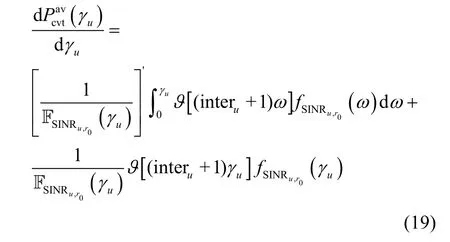
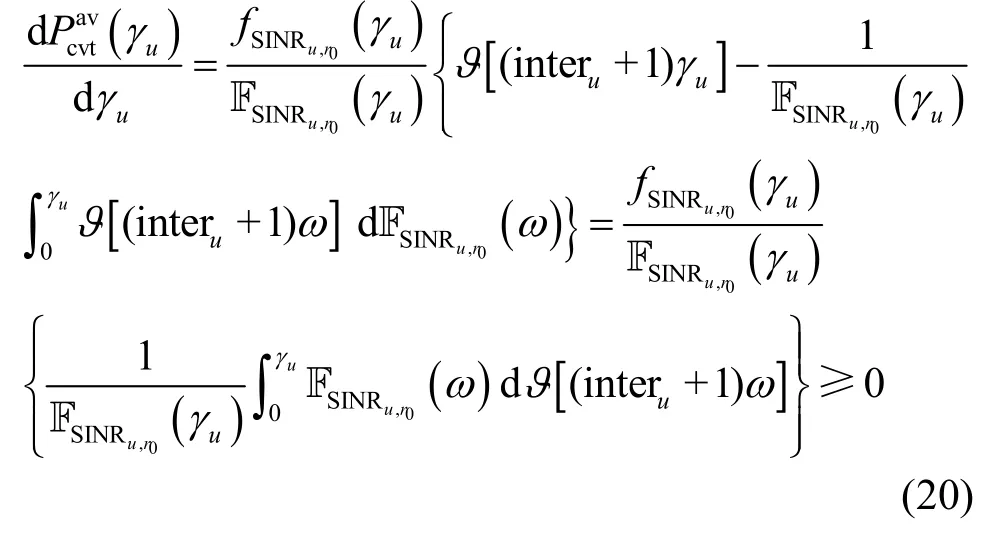
因此 EUR在定义域上单调递增,若假设γu=Δi是 ηEU=τ的解,则只需保证 γu≥Δi即可满足约束式(15)。
通过上述分析,若令Ωi=max {Φi,Δi,Σi,Oi},则[Ωi,∞)即为切换门限的可行域。在此基础上,通过一维线性搜索算法可得到使STP最大的最优解,如算法1所示。
算法1切换门限选择算法
输入λu,λr, λe,Rc,Rs,Ec,α,T,Pr,Mr,Ψ,a,b,M等系统参数
输出最优门限γopt

4.4 复杂度分析
本节分析本文安全传输方案的复杂度,选择文献[25-26]中ZFBM算法作为对比方案。考虑到不同用户的硬件电路存在差异(a、b、M不同),针对不同用户可设置不同的切换门限,其计算复杂度可表示为O(Ψ);而ZFBM算法的计算复杂度可表示为O(ΨM2r)(M≥Ψr)或O(Ψ2Mr)(Ψ≥Mr)。综合来看,虽然本文所提方案的全局flop数(一个flop表示一次实数乘法或加法运算)相比于传统策略下的ZFBM方案有所提升,但方案整体的计算复杂度仍维持在同一量级。
5 仿真分析
本节针对所提传输方案的性能进行数值分析与仿真验证。假设信道衰落系数α=4,周期Tdl=1,所有RC的发射功率Pr= 2 0W 、天线数Mr= 1 0、服务用户数Ψ=6,目标速率与目标安全速率分别为Rc= 2 bit⋅(s⋅ H z)-1、Rs=0 .6 bit⋅(s⋅ H z)-1,RC、ECU以及PE的密度分别为NLM中RF-to-DC电路参数为M=6 2 mW、a=80、b=0.062[18]。
NLM与LM(η= 0 .7)下的能量转换关系如图3所示。由图3可知,NLM在合理性上有明显提升,体现在以下两方面:1)由于能量采集电路的敏感门限较高,当输入功率较小时(图中低效率区域),NLM 的转换效率也非常低但维持缓慢增长,敏感门限(Pin= 3 0mW)附近的转换效率连续变化,这相比于LM下由η=0到η=0.7的阶跃式跳变,更加符合系统的实际表现;2)考虑到接收端硬件配置简单、处理能力有限,一般无法承载过高的输出功率,因此NLM对RF-to-DC电路设置输出功率限制。当输入功率较大时(图中输出功率饱和区),转换功率逐渐趋于饱和并无限接近于Pmax=6 2 mW,这避免了LM下转换功率可随输入功率无限增长的不合理情形。

图3 非线性/线性能量转换曲线
另外,NLM 中的转换效率(CE, conversion efficiency)随输入功率动态变化:输入功率较低时,CE也维持在极低的范围内,大部分能量未被有效利用;随着输入功率的增长,CE同步提升;而当输入功率超出一定范围,输出进入饱和区,输入功率的增长对能量收益的提升作用越发有限,CE转而出现下降的趋势,这对于能量资源是得不偿失的。这种动态的CE相比于LM中的恒定CE更值得关注。而本文在关注CE的同时,考虑路径损耗对能量效率的影响,将EUR作为WPT的效率指标,这与绿色通信的理念是契合的。
切换门限对 WPT稳定性和效率的影响如图 4所示。由图4可知,EOP随门限单调递减、EUR随门限单调递增,与4.3节单调性分析结果一致。其中EOP在 γu<-5dB时稳定于1,这是因为切换门限较低时,传能时长TP较短,导致满足能量需求Ec所需的最低蓄电功率高于RF-to-DC电路的输出功率限制Pmax,则能量中断的概率趋于 1;随着切换门限的增加,EOP快速下降,而当 γu≥0.8 dB时,EOP降至0,这是因为切换门限较高时,传输能量的时间较长,仅接收的干扰与噪声功率就可采集到高于Ec的能量,则能量中断的概率趋于0。
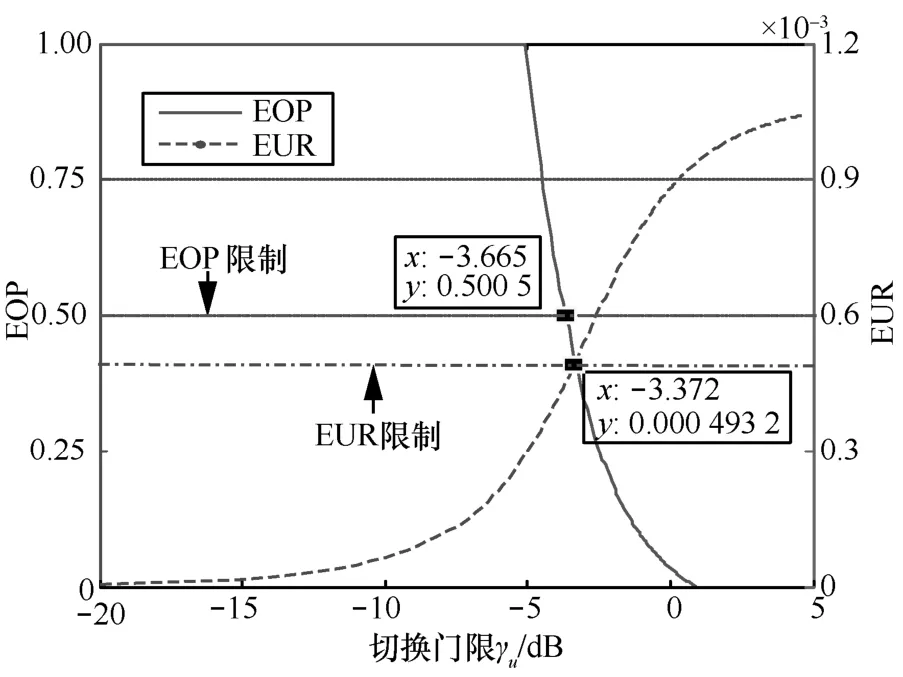
图4 切换门限对能量传输性能的影响
切换门限对WIT性能的影响如图5所示,图中“-nc”后缀曲线表示窃听者独立窃听,“-c”后缀曲线表示联合窃听。结合 STP的定义,为了更加直观地对比分析,图5给出COP、SOP的互补概率曲线,即 CCOP与 CSOP。由图 5可知,CCOP与CSOP随门限单调递增,与4.3节COP、SOP分析结果一致。这是因为增加切换门限提升了WIT的平均信道质量,提升了信息传输质量(包括可靠性与安全性)。但切换门限约束着 WIT的发生概率,且随门限的增加单调递减。根据STP定义可知,ASR和ITD会同时影响STP,但切换门限对ASR和ITD的影响是此消彼长的博弈关系,因此STP随着切换门限的变化呈现出非单调变化的趋势。又由于当uγ→∞时,pit→0导致ξ→0,因此STP先增加后减少,即存在一个最优的切换门限可使STP取得最大值。

图5 切换门限对信息传输性能的影响
另外,可以发现当窃听者联合窃听时,可达STP下降明显,但最大STP时的切换门限则显著提高。这是由于面临的窃听威胁越强,提升信道质量来保证安全传输的需求越高,从而达到ASR与ITD的最优折中。
最优切换门限值与窃听者密度的关系如图6所示。窃听者密度越高,造成的威胁越大,保证信息安全对信道资源的要求就越高,因此在各项约束充分松时(τ=0 , ι=μ=ο=1),最优切换门限随着窃听者密度的增加而增加,其中包括窃听者独立窃听(图6中“-nc”后缀曲线)与联合窃听(图6中“-c”后缀曲线)2种情况。而随着约束的收紧,则需要以一定的性能损失为代价来满足各项指标的要求。仿真实验中,令 τ=0 .5× 1 0-3,ι=0.4,μ=ο= 0 .5,则由图6可知,EUR、EOP、COP、SOP-nc与SOP-c约束对应的最低切换门限分别为-3.37dB、-3.66 dB、-5.08 dB、-4.31 dB(独立窃听)和0.08 dB(联合窃听)。因此,对于窃听者独立窃听的场景,EUR约束最强,且由于松约束下的最优门限取值始终无法满足 EUR的最低要求,最终切换门限即为 EUR约束对应的最低门限-3.37 dB(图6中“-nc-wc”后缀曲线);而对于窃听者联合窃听的场景,SOP约束最强,松约束下的门限取值在窃听者密度较低(λe<0.057)时未能满足其要求,需将切换门限设定在 SOP约束对应的最低门限 0.08dB(图 6中“-c-wc”后缀曲线)。单项约束的松紧性影响着最终切换门限的取值,单项约束越紧,最终门限取值与松约束下最优门限的差距越大,损失的STP也越多。
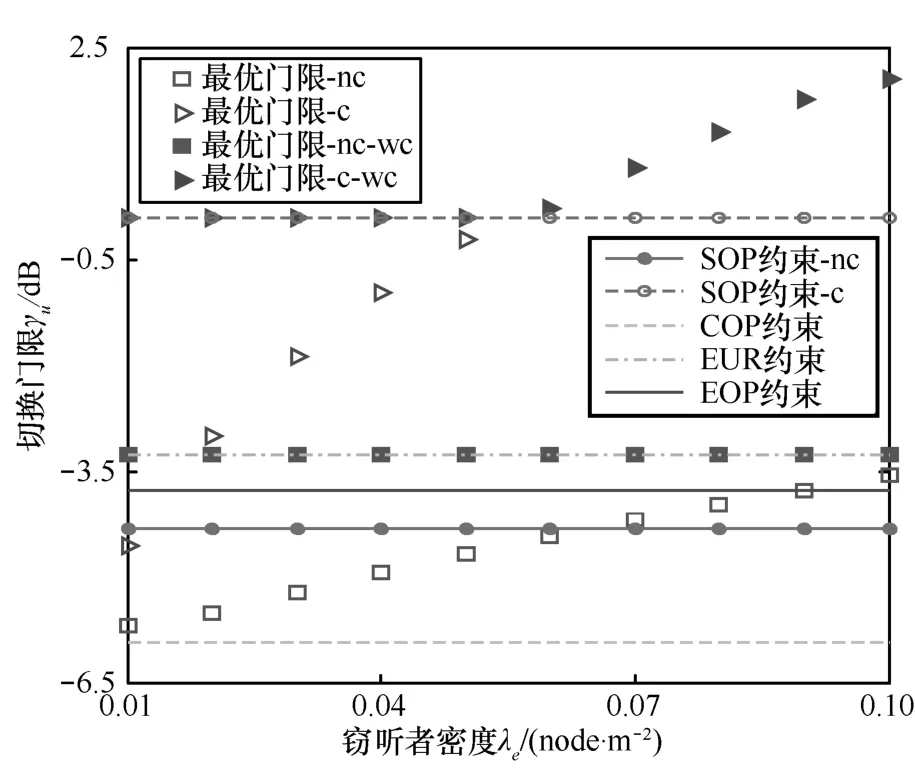
图6 最优切换门限值与窃听者密度的关系
在独立窃听与联合窃听这 2种场景下可达 STP与窃听者密度的关系如图7所示。由图7可知,数值结果与仿真结果吻合,说明了推导过程的正确性。另外,与传统策略ZF波束传输方案相比(图7中“-tr”后缀曲线),在窃听者独立窃听(图7中“-nc”后缀曲线)与联合窃听(图7中“-c”后缀曲线)场景中,DIPS方案均可在保证能量约束的同时有效提升系统平均STP。其中DIPS方案在窃听者独立窃听时提供的安全增益更为显著,随窃听者密度的增加而逐渐减少,这是因为随着窃听者的增强(能力增强或密度增强),对抗其窃听的难度也在逐渐增加。而在窃听者联合窃听场景中,当窃听者密度较低时,因SOP约束造成的STP损失非常明显(图7中“-ideal”后缀曲线表示无约束条件下的 STP),但由图 7可知,λe=0.01时,DIPS方案仍可将STP提高34.15%左右。另外,当窃听者密度增加到一定程度后,传统策略ZF方案的可达STP非常有限,系统几乎无法安全通信,但DIPS方案STP仍可保持在一定水平。综上所述,本文所提方案能够有效地提升信息传输的可靠性和安全性。

图7 不同窃听者密度条件下,不同方案的保密吞吐量
6 结束语
本文在时域切换型携能通信系统中提出一种机会安全传输方案。首先,考虑一个多小区、多用户、多窃听者的携能通信网络,并假设用户采取时域切换型接收机且以非线性模型采集能量。其次,考虑到能量传输与信息传输的差异性安全需求,结合无线信道的时变性,提出了基于信干噪比门限的动态信息能量切换传输方案,并综合分析了能量传输和信息传输的性能。然后,分析了切换门限对系统性能的影响,为使系统性能最佳,在满足能量需求,保证可靠性、安全性的前提下,最大化系统的保密吞吐量。最后,仿真证明了所提方案的有效性。
附录A 定理1 证明

附录B 定理5 证明
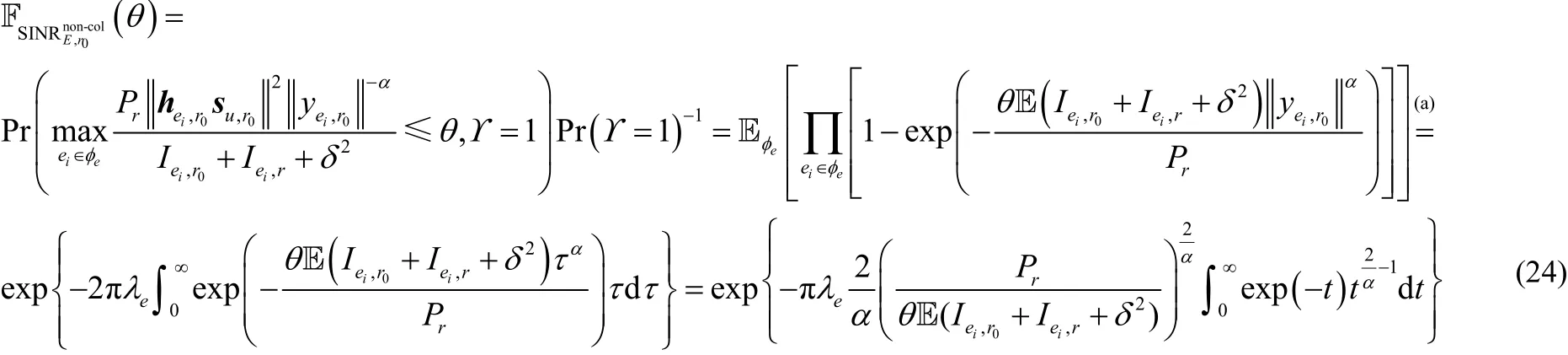
其中,由PPP的概率生成函数(PGF, probability generating functional)可得(a)处等号成立。

附录C 定理6 证明
当PE联合窃听时,其接收SNR的拉普拉斯变换可表示为

其中,由PPP的PGF可得(b)处等号成立,由信道衰落与PPP分布相互独立可得(c)处等号成立,由Gamma函数的性质得到[27](d)处等号成立。

证毕。
