混合地理加权似乎不相关模型的估计

刘 超，桂风云

（1.北京航空航天大学 数学与系统科学学院，北京100191；2.中央民族大学 理学院，北京100081）

0 引言

时空数据分析在统计学和计量经济学领域受到越来越多的关注。时空数据不同于一般的截面数据和时间序列数据，同时具有空间和时间上的特性。社会科学领域常用的时空数据模型为空间面板数据模型，有关时空数据模型的介绍可参考Anselin（1988）[1]和Elhors（t2014）[2]。

实际问题分析中，因变量和自变量之间的关系往往会随着空间和时间的改变而发生变化，这就是时空异质性。传统的空间面板数据模型一般都是单独考虑空间异质性和时间异质性，将二者同时考虑的模型还很少见，其中桂风云和魏传华（2016）[3]将地理加权回归技术用于空间似乎不相关模型，提出了地理加权似乎不相关模型，Wei等（2017）[4]进一步研究了该模型的估计问题。这一新模型适合空间观测点个数较多，时间观测点较少的传统空间面板数据，利用地理加权回归技术刻画空间异质性，利用似乎不相关结构刻画时间异质性。该模型在结构上是一类空间变系数似乎不相关模型，假设了不同时刻的回归系数都是随着空间位置变化而变化的。然而实际问题中，更为一般的情形是有一部分回归系数会随着地理位置的变化而变化，而另一部分系数不随地理位置的改变而改变。基于这一考虑，本文提出一类混合地理加权似乎不相关模型（简称MGW-SUR模型），并研究该模型的估计问题。

1 混合地理加权似乎不相关模型的设定

在桂风云和魏传华（2016）[3]的基础上，考虑如下的混合地理加权似乎不相关模型

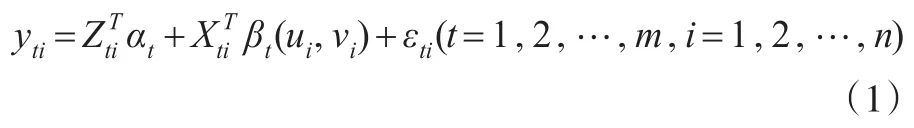
其中Yti和Xti=(xti1，xti2，…，xtip)T，Zti=(zti1，zti2，…，分别为i观测点t时刻的因变量与自变量观测值，和分 别为未知的常值系数向量和系数函数向量。模型（1）可记为如下矩阵形式：

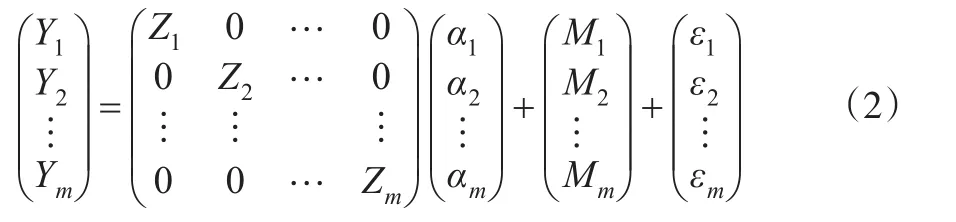
其中：

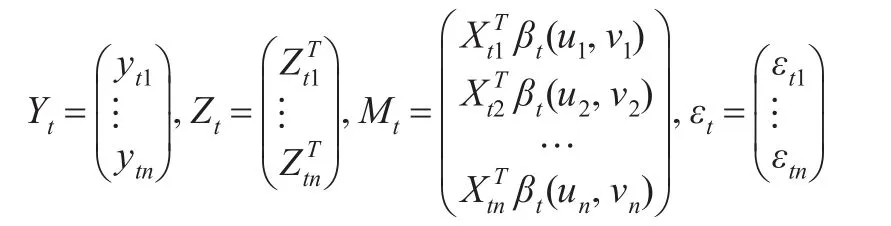
显然，该模型是由m个混合地理加权回归模型组成的，这m个模型通过如下模型误差之间的相关性建立联系：

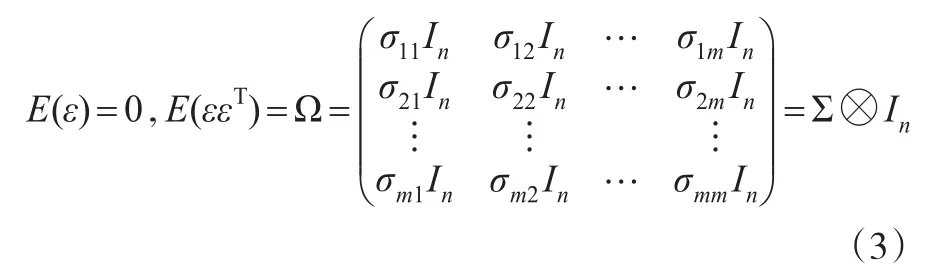
其中Ω是模型误差项的协方差矩阵；Σ是同一观测点上误差项的协方差矩阵。

MGW-SUR模型（2）和模型（3）将混合地理加权回归模型和似乎不相关模型相结合，能够同时刻画时空数据的时间异质性和空间异质性,是普通的空间似乎不相关模型和地理加权似乎不相关模型的推广。

2 混合地理加权似乎不相关模型的估计

混合地理加权似乎不相关模型中既有随着地理位置变化而变化的非参数系数函数，也有常值系数。同其他类型的半参数模型一样，重点关注常值系数的估计。对于普通的线性似乎不相关模型，众所周知，如果不考虑模型之间的相关性，那么多个子模型的联合估计等价于子模型的单独估计，而将模型的相关性考虑进去构造的广义最小二乘估计更有效。对于本文所提的MGW-SUR模型，将给出两种估计方法，分别对应不考虑子模型之间的相关性和考虑这种相关性。

2.1 不考虑协方差矩阵的普通估计

如果不考虑子模型之间的相关性，那么本文将分别对子模型进行单独估计。此时子模型就是一个普通的混合地理加权回归模型。本文采用基于局部线性光滑方法的两步估计法（profile最小二乘法）对模型进行估计。时间点t处对应的子模型为：

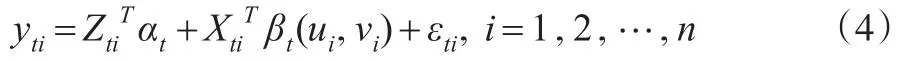
首先，假定常系数αt已知，则模型（4）可以写成：

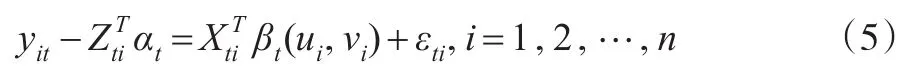
显然，模型（5）是标准的地理加权回归模型，基于Wang等（2008）[5]局部线性光滑方法，可得βt(ui，vi)的估计为：

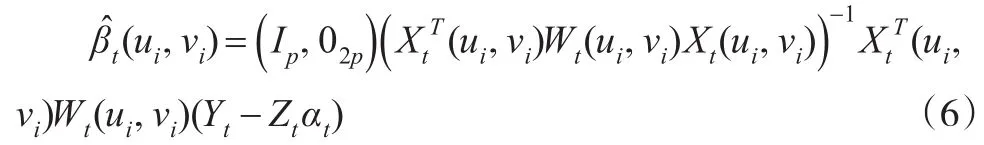
将式（6）代入原模型（4）中，可以得到下面的模型：

其中：

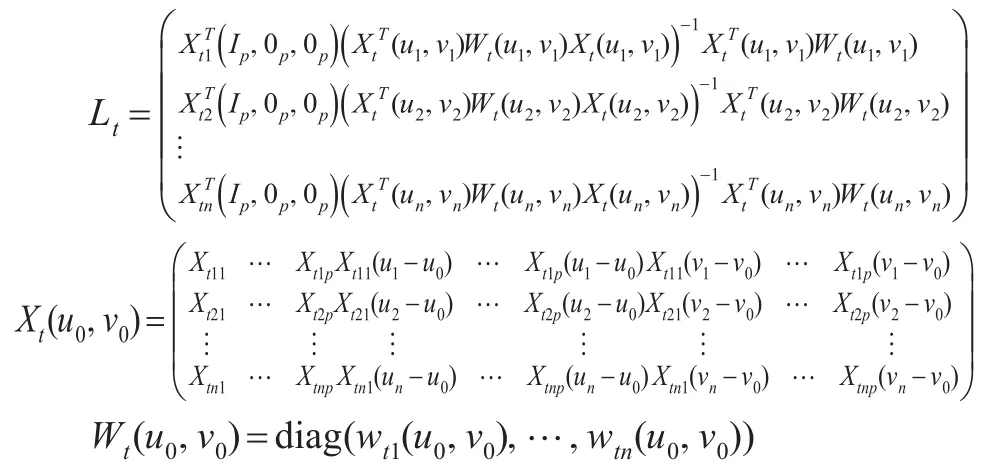
其中wti(u0，v0)作为一个权函数值表示t时间点上第i组因变量和自变量观测值Xti，yti对估计(u0，v0)处的系数函数所起的重要性。同桂风云和魏传华（2016）[3]，本文设置为：

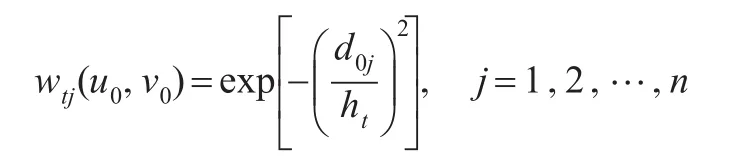
其中d0j表示空间位置(u0，v0)和(uj，vj)之间的距离，ht＞0称为光滑参数，可以用交叉证实法来选取,详细介绍可参考Fotheringham等（2003）[6]。

采用普通最小二乘估计法来估计（7），可以得到常值系数αt的估计是：

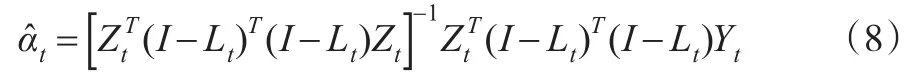
从而变系数函数的估计为：

进而得到Yt的拟合值：

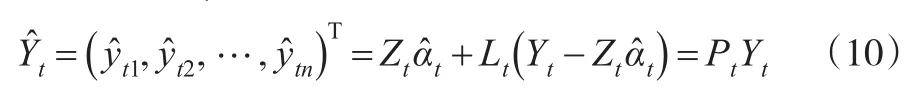
从而模型拟合为：

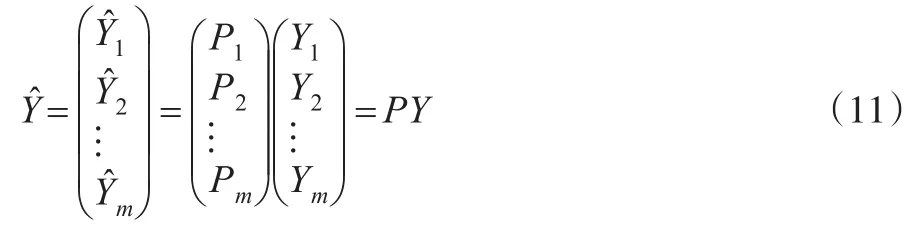
其中：

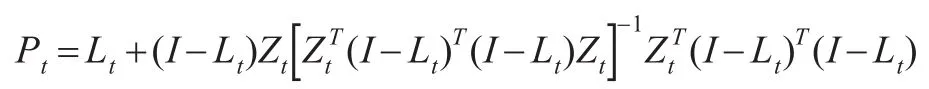
2.2 考虑协方差矩阵的广义估计

上文的普通估计没有考虑子模型之间的相关性，为了构造更为有效的提高估计，本文提出一类广义两步估计。先假设常值系数已知，则模型可以转化为标准的地理加权似乎不相关模型：

其中：

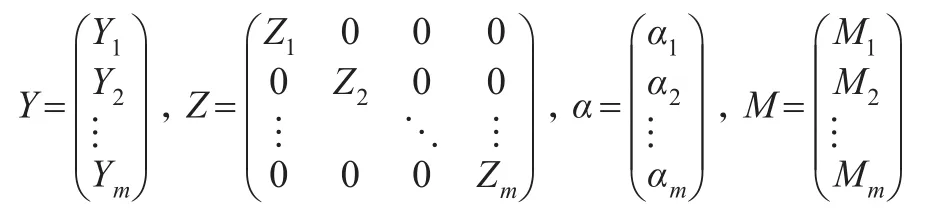
由Wei等（2017）[4]，的有效估计定义为：

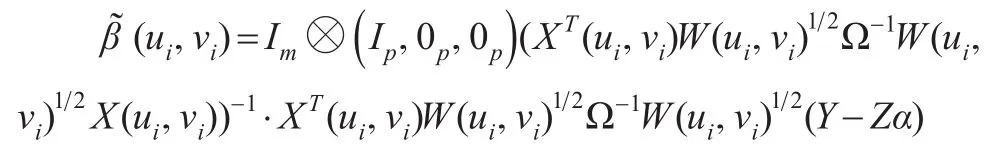
其中，Ω由式（3）定义。

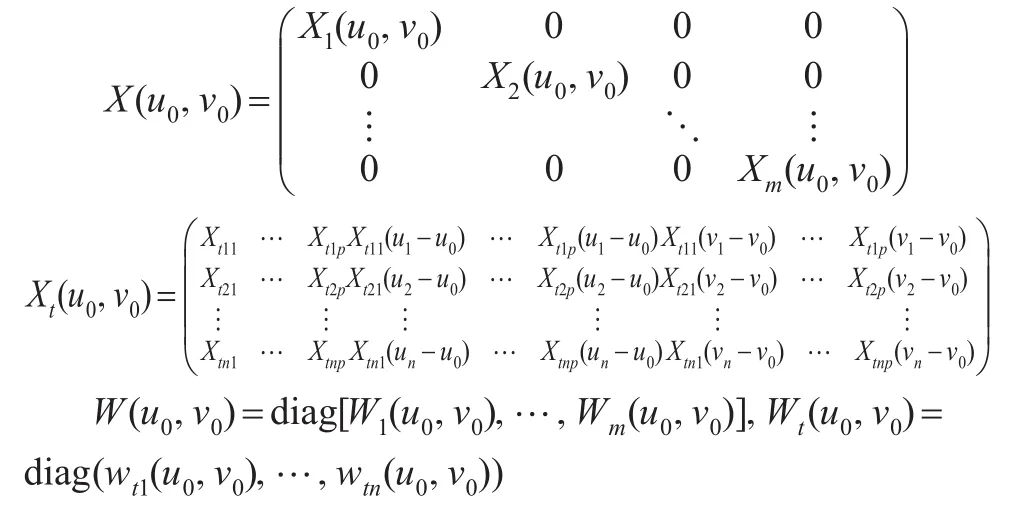
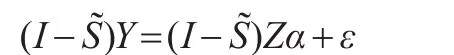
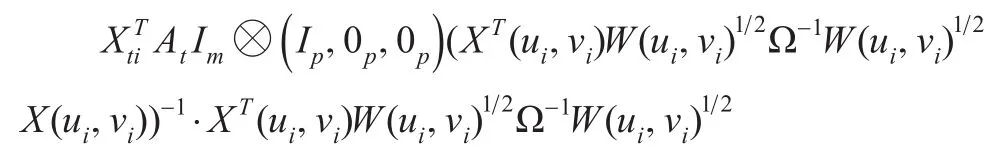
由广义最小二乘估计法可以得到常值系数的估计：

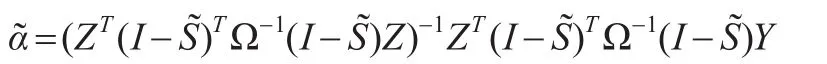
相应的变系数函数的估计为：

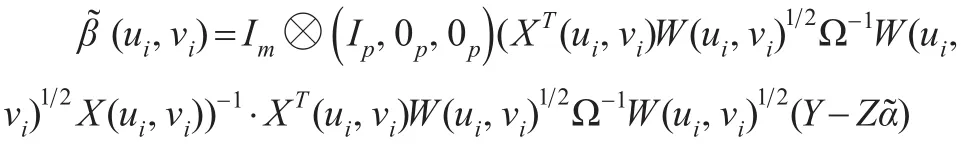
进而得到因变量拟合结果：

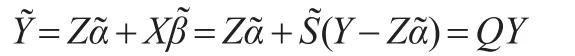
其中：

针对MGW-SUR模型的广义局部线性加权最小二乘两步估计，有如下性质：

定理1：常值系数的广义局部加权最小二乘估计量的期望和方差分别为：

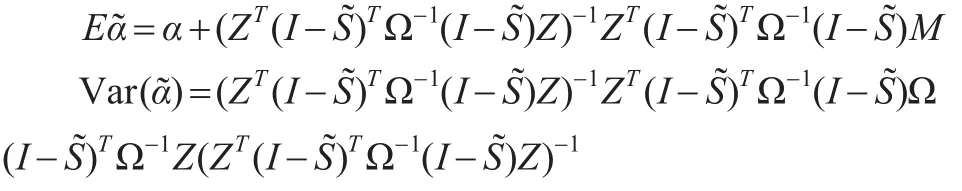
3 模拟实验

本文通过数值模拟来验证所提的两种估计方法的有效性。模拟实验中，空间位置的选取是通过二维格子空间来定义的，在每个m×m个格子点上取观测值，观测点之间的距离可以通过格子空间的横、纵坐标来求得。在平面直角坐标系中，这n=m2个点的坐标定义为：

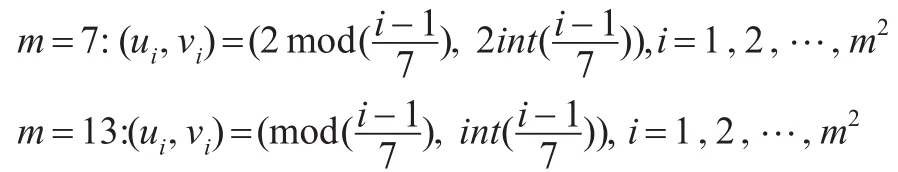
假设数据来自下面的模型：

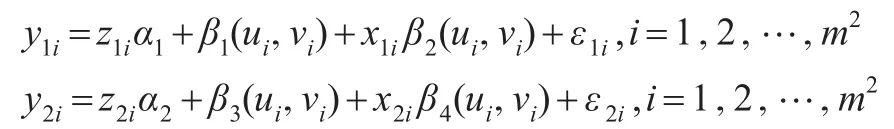
其中自变量的取值为x1i～U(- 1，1)，x2i～N(0 ，1)，z1i～U(0 ，1)，z2i～N(1 ，1),常值系数为α1=2，α2=3，系数函数分别为：

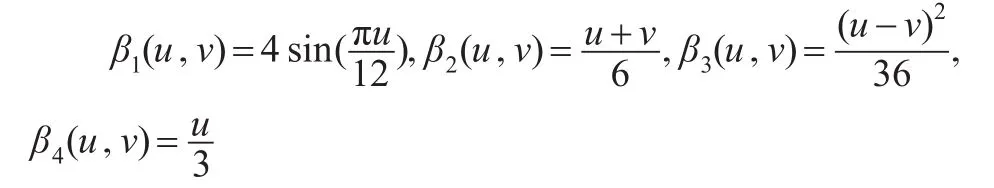
误差之间的相关性满足：

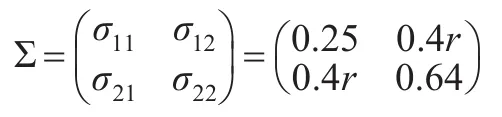
权函数采用下面的形式：

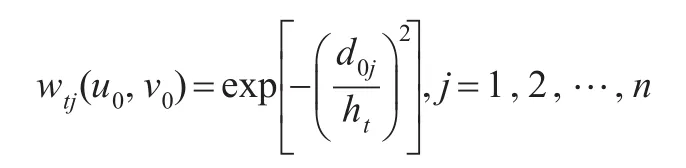
为简化计算过程，实际操作中假设不同时间点对应的窗宽ht=h是相同的，通过交叉验证（CV）进行选择。误差相关系数分别取r=0.5，0.8两种情况，样本数量n=m2，其中m=7，13两种情况，对每种情况重复实验1000次。

本文重点关注常值系数的表现，利用1000次重复中得到的估计量的均值（Mean）、标准差（SD）和估计均方误差来考察其表现，其中估计均方误差（EMSE）定义为:

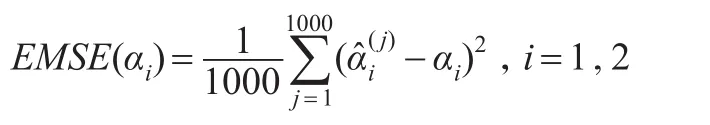
其中表示第j次重复时得到的估计值。

模拟实验结果如表1所示。可以看出，随着样本量的增加，两种估计的效果都越来越好。并且随着误差相关性的增加，广义最小二乘估计比普通最小二乘估计表现更好。

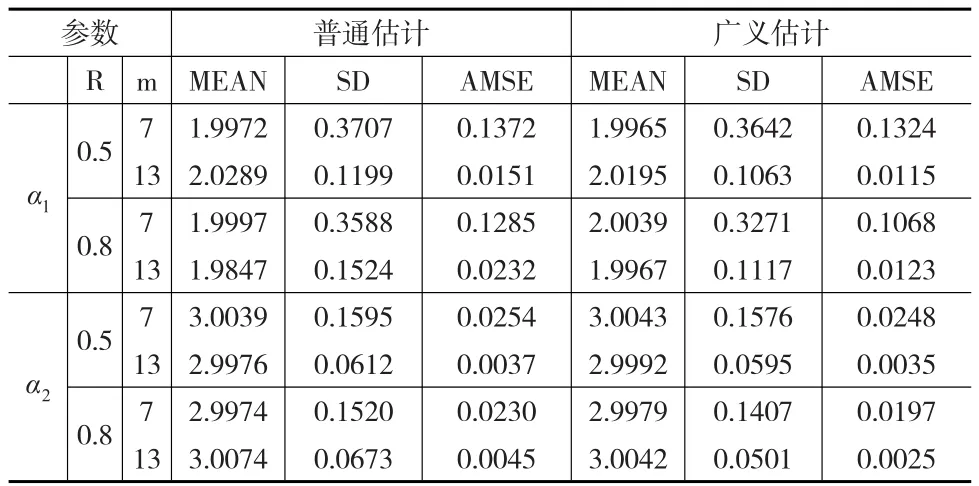
表1 混合地理加权似乎不相关模型两种估计的实验模拟结果

4 结论

本文研究了一种能够同时刻画时空数据的时间异质性和空间异质性的混合地理加权似乎不相关回归模型，并且研究了模型的两种估计方法：一是不考虑模型误差相关性的普通局部线性加权最小二乘两步估计，二是考虑模型误差相关性的广义局部线性加权最小二乘两步估计。本文重点研究了所提模型的估计问题，关于MGW-SUR模型的统计检验，以及模型在实际应用中的表现都还有待进一步研究。