斜坡型需求率且短缺量部分拖后的改良品库存模型

张云丰，王 勇，龚本刚

（1.安徽工程大学 管理工程学院，安徽 芜湖 241000；2.重庆大学 经济与工商管理学院，重庆 400030）

0 引言

改良品（Ameliorating Items）在库存持有期间会随着时间的推移而发生重量增加、数量增长或质量改善的现象，从而使物品的经济价值或效用得到提升。改良品广泛存在于农业、渔业、家禽养殖业等行业，如养殖场中处于生长期的肉鸡、猪栏中的育肥猪及种猪、果园中尚未采摘的水果，鱼塘中具有高度繁殖率的鱼类、酒庄中的高档酒类等。Wee等（2008）指出少量的改良品订货可凭直觉或经验完成而影响不大，对大规模的改良品订货问题，按照科学合理的方法进行是非常必要的。Chou等（2008）指出改良品在存储期的特点与易变质品正好相反，其订货问题值得开展深入研究。

一些产品在刚进入市场时，消费者对其需求率往往随时间呈增长趋势，待达到稳定阶段后，需求率才保持恒定。“斜坡型”需求则较形象地描述了需求率的这种特征，并引起学者们广泛的关注，相关的研究成果也甚为丰富。本文在前人研究的基础上，结合改良品的库存特点，考虑允许缺货且短缺量部分拖后供应，建立改良品库存模型，并寻求改良品最优库存补充策略。需要说明的是，在改良品与易变质品库存持有期间，虽然两者物理特性上的变化可视为互逆过程，但由于产品的改良需要承担相应的改良成本，因此，改良品比易变质品的总成本函数也更为复杂。

1 基本假设与符号说明

本文在建立改良品库存模型过程中使用的基本假设和符号说明如下：

（1）每次补充的数量恒定且补充速率无穷大；

（2）零售商订货提前期为零；

（3）允许缺货且短缺量部分拖后，拖后率为β；

（4）B为拖后补充的最大短缺量，B′为理论最大短缺量，满足B=βB′；

（5）T为固定的订货周期长度；

（6）Co为每次订货的订购成本；

（7）Cr为每单位改良品的采购成本，记单位采购成本；

（8）Ch为每单位改良品单位时间的存储成本，记单位存储成本；

（9）Cs为每单位改良品单位时间的缺货成本，记单位缺货成本；

（10）Ca为库存期间因改良而增加单位物品的改良成本，记单位改良成本；

（11）Cd为每单位改良品因失去销售机会而引起的机会成本，记单位机会成本；

（12）θ为单位时间物品的改良率，库存期间保持恒定且0＜θ＜＜1；

（13）S为每个订货周期[0，T]内的最大库存水平，即S=I(0)；

（14）I(t)为每个订货周期[0，T]内任意时刻t的库存水平；

（15）t1为每个订货周期[0，T]内库存水平降为零的时刻；

（16）R(t)为斜坡型需求率，满足R(t)=D[t-(t-μ)H(tμ)]，D＞0，H(t-μ)是Heaviside函数为需求拐点（线性需求部分与常数需求部分的交叉点）。

2 改良品库存模型

每个订货周期[0，T]分为两个阶段：第一阶段为[0，t1]，本阶段在市场需求和自身改良的共同作用下，库存水平从0时刻的最大值S下降到t1时刻的零库存；第二阶段为[t1，T]，本阶段一直处于缺货状态，其中，β比例的顾客继续等待，需求在下一次补充时得到满足，而(1-β)比例的顾客不能容忍缺货，放弃继续等待。整个订货周期[0，T]内的需求变化用以下两个微分方程刻画为：

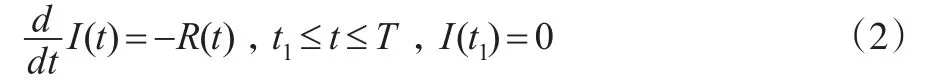
根据需求拐点μ与零库存时刻t1的关系，需要分两种情形来建立改良品库存模型。

2.1 模型一 0≤μ≤t1(见图1)

在该情形下，微分方程（1）和方程（2）转化为：

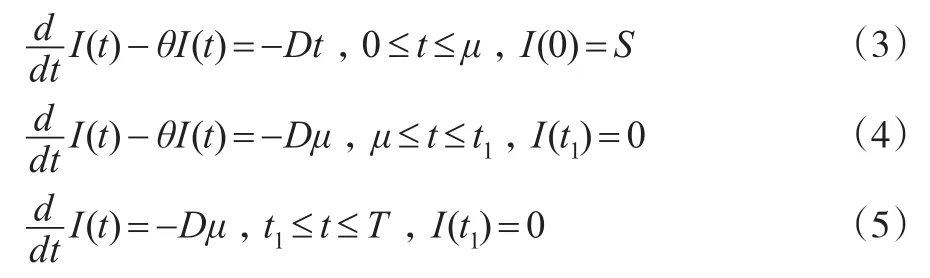
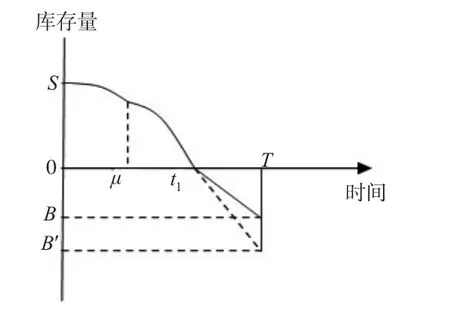
图1 0≤μ≤t1时的库存模型

结合边界条件，解微分方程（3）至方程（5），得到：

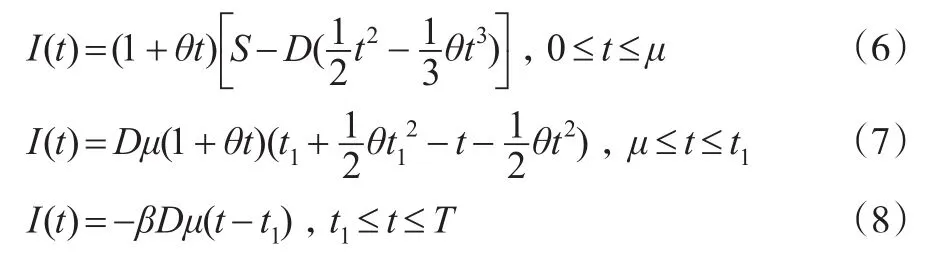
结合I(μ-)=I(μ+)，可知：

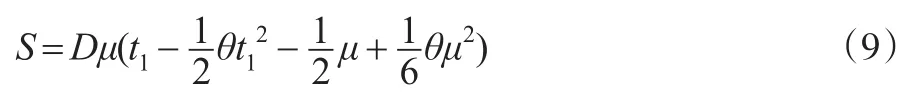
因此，在一个完整的订货周期[0，T]内，物品改良的总数量为：

考虑到0＜θ＜＜1，故在计算过程中略去θ的二次及以上项，下同。

最大短缺量和失去销售机会的需求量分别为：

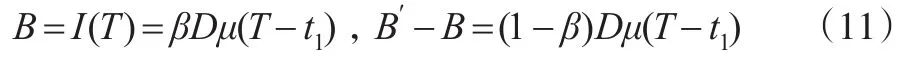
零售商在一个订货周期[0，T]内的总成本由订货成本OC1、采购成本PC1、库存成本HC1、缺货成本SC1、改良成本AC1及机会成本KC1六部分组成：

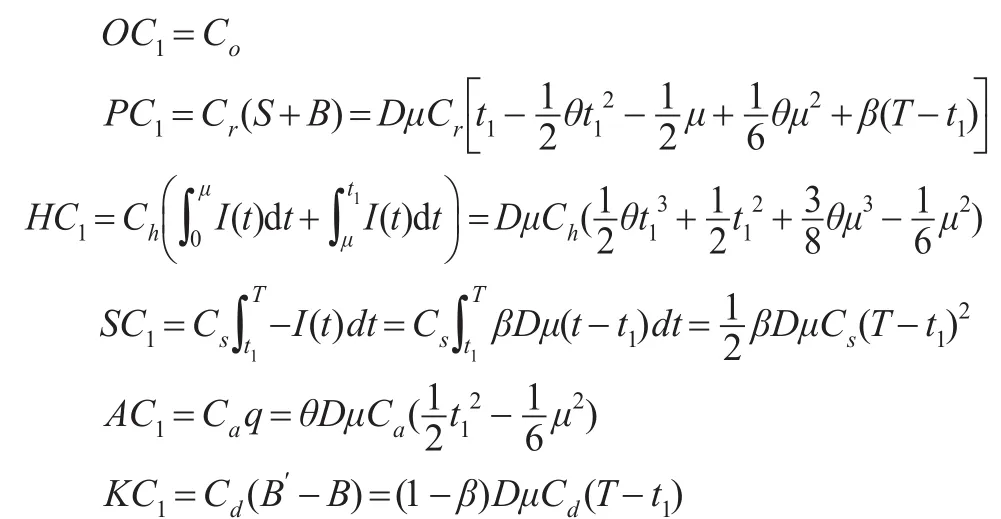
零售商的单位时间总成本为：

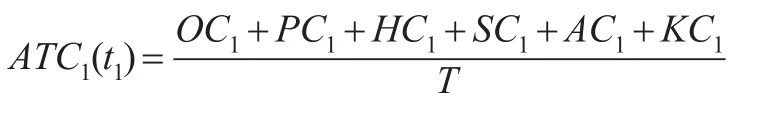
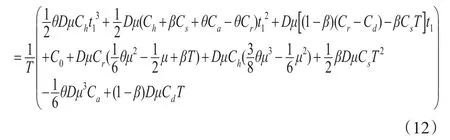
零售商单位时间总成本取得最小值的必要条件是：

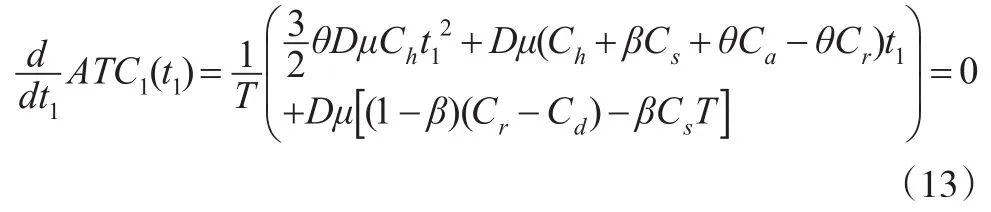
经化简后得到：

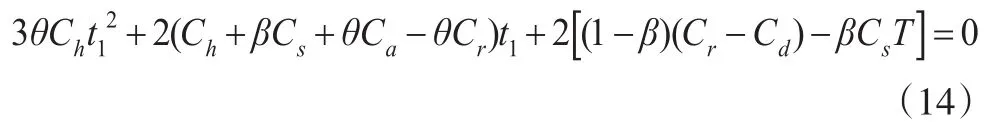
令L1=3θCh，M1=2(Ch+βCs+θCa-θCr)，N1=2[(1-β)(Cr-Cd)-βCsT]，则式（14）转化为：

显然，有L1＞0，M1＞0(0＜θ＜＜1)。因此，当且仅当N1-M12/4L1≤0时，存在唯一正根M1)/2L1满足题意。若：

则零售商单位时间总成本取得最小值的充分条件成立。用替代式（9）中的t1，得到每个订货周期初最优库存水平：

每个订货周期末最大短缺量：

零售商每次最优订货数量：

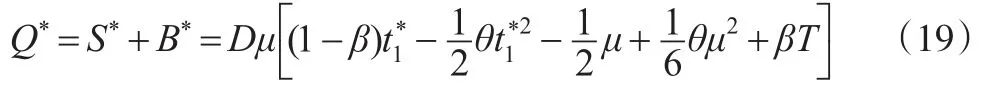
零售商最小单位时间总成本：

2.2 模型二t1≤μ≤T(见图2)

在该情形下，微分方程（1）和方程（2）转化为：

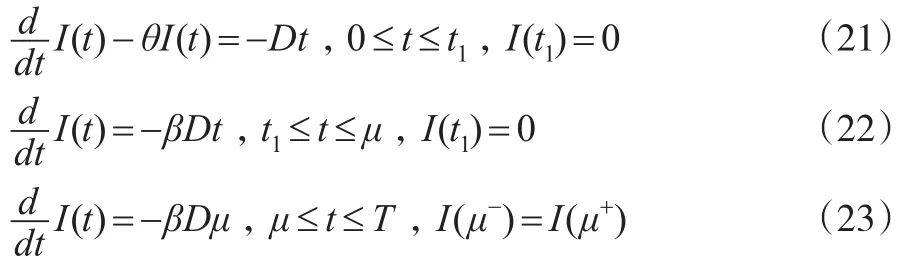
结合边界条件，解微分方程（21）至方程（23），得到：

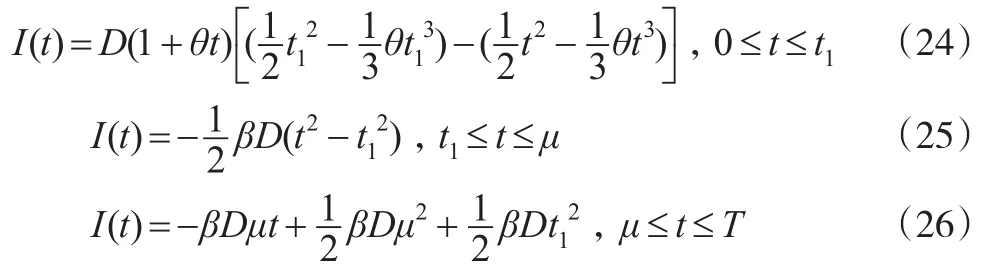
考虑到I(0)=S，可知：

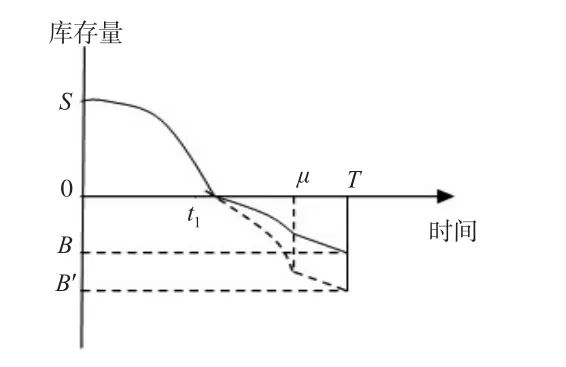
图2 t1≤μ≤T时库存模型

因此，在一个完整的订货周期[0，T]内，物品改良的总数量为：

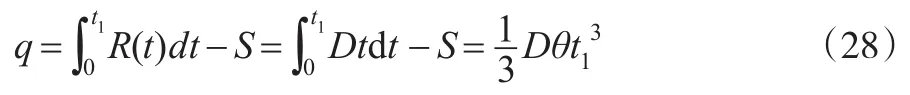
最大短缺量和失去销售机会的需求量分别为：

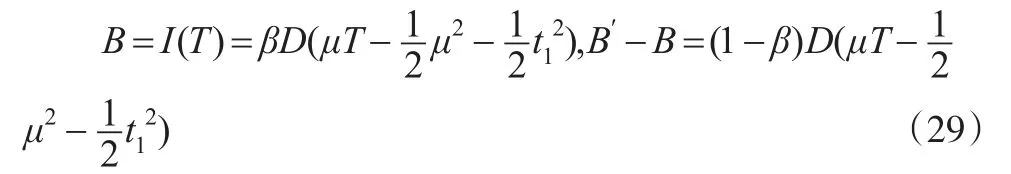
零售商在一个订货周期[0，T]内的总成本由订货成本OC2、采购成本PC2、库存成本HC2、缺货成本SC2、改良成本AC2及机会成本KC2六部分组成：

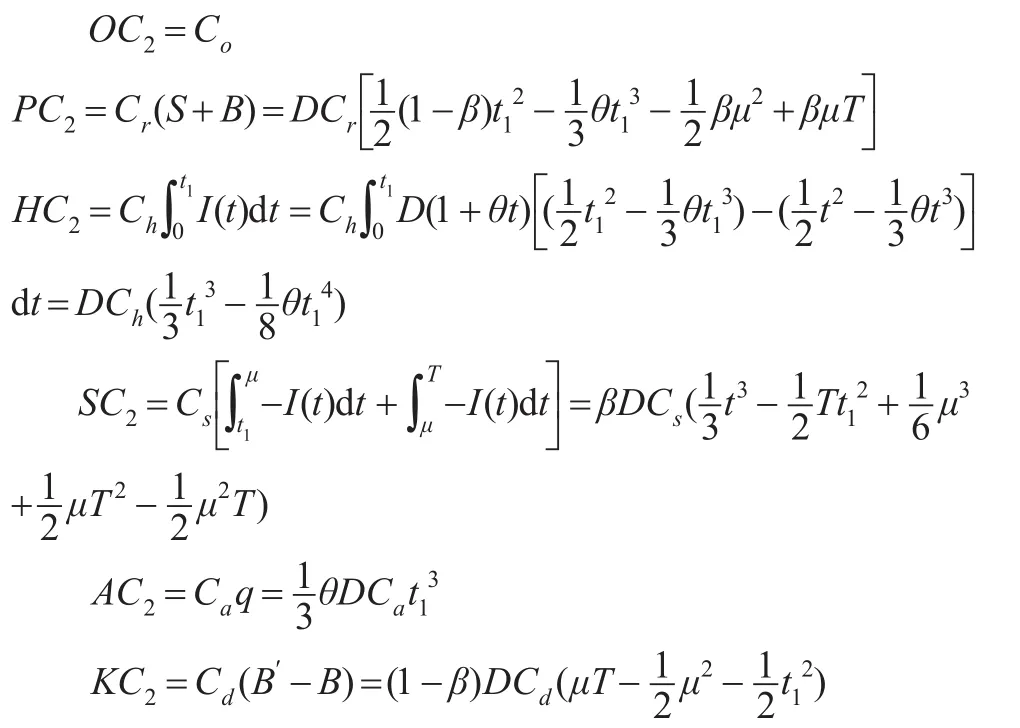
零售商的单位时间总成本为：

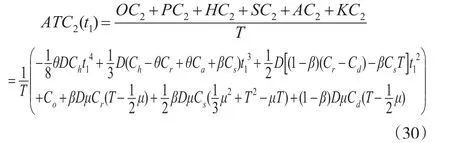
零售商单位时间总成本取得最小值的必要条件是：

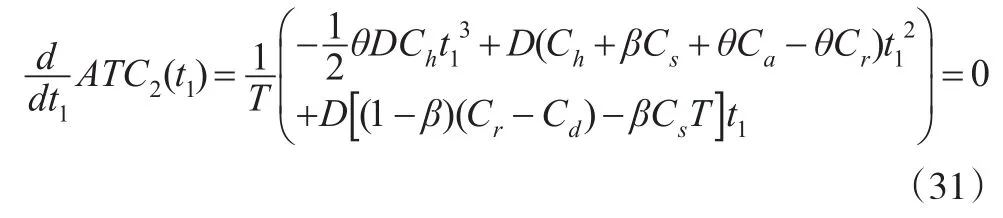
考虑到t1≠0，经化简后得：

令L2=θCh，M2=-2(Ch+βCs+θCa-θCr)，N2=-2[(1-β)(Cr-Cd)-βCsT]，则式（32）转化为：

显然，有L2＞0，M2＜0(0＜θ＜＜1)。因此，当且仅当N2-/4L2≤0时，存在唯一正根t1==(-M2-满足题意。若：

则零售商单位时间总成本取得最小值的充分条件成立。用替代式（27）中的t1，得到每个订货周期初最优库存水平：

每个订货周期末最大短缺量：

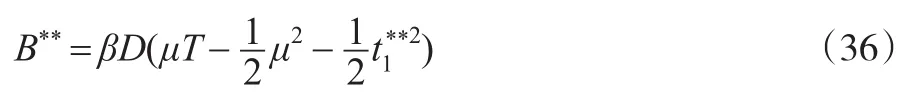
零售商每次最优订货数量

零售商最小单位时间总成本：

3 数值算例及敏感性分析

3.1 数值算例

例1：对模型一中各参数赋值如下：Co=50元/次；Cr=10元/单位；Ch=5元/单位·年；Cs=6元/单位·年；Ca=4元/单位；Cd=16元/单位；D=100单位，μ=0.12年；θ=0.1；β=0.8；T=1年。将上述参数代入式（14），解得=0.621。经验证，=0.621满足式（16）取得最优值的充分条件。同时，解得每个订货周期初最优库存水平S*=6.504，每个订货周期末最大短缺量B*=3.638，则零售商每次最优订货数量Q*=S*+B*=10.142；零售商的单位时间总成本=183.171。

例2：对模型二中各参数赋值如下：Co=50元/次；Cr=10元/单位；Ch=5元/单位·年；Cs=6元/单位·年；Ca=4元/单位；Cd=16元/单位；D=100单位，μ=0.90年；θ=0.1；β=0.8；T=1年。将上述参数代入式（31），解得=0.664。经验证，=0.664满足式（33）取得最优值的充分条件。同时，解得每个订货周期初最优库存水平S**=21.069，每个订货周期末最大短缺量B**=21.964，则零售商每次最优订货数量Q**=S**+B**=43.033；零售商的单位时间总成本=640.614。

3.2 敏感性分析

下面将考察改良率θ、拖后率β、单位缺货成本Cs、单位机会成本Cd及单位改良成本Ca变动+25%、+10%、-10%、-25%时，对上述模型一和模型二中主要决策变量值的影响情况，分别见表1和表2所示。为了便于对敏感程度做出说明，给出如下规定：若δ∈[0，10%)，则不敏感；若δ∈[10%，30%)，则稍敏感；若δ∈[30%，60%)，则较敏感；若δ∈[60%，100%)，则很敏感；若δ∈[100%，+∞)，则极敏感。其中，δ表示因变量变动比率与自变量变动比率的绝对值。

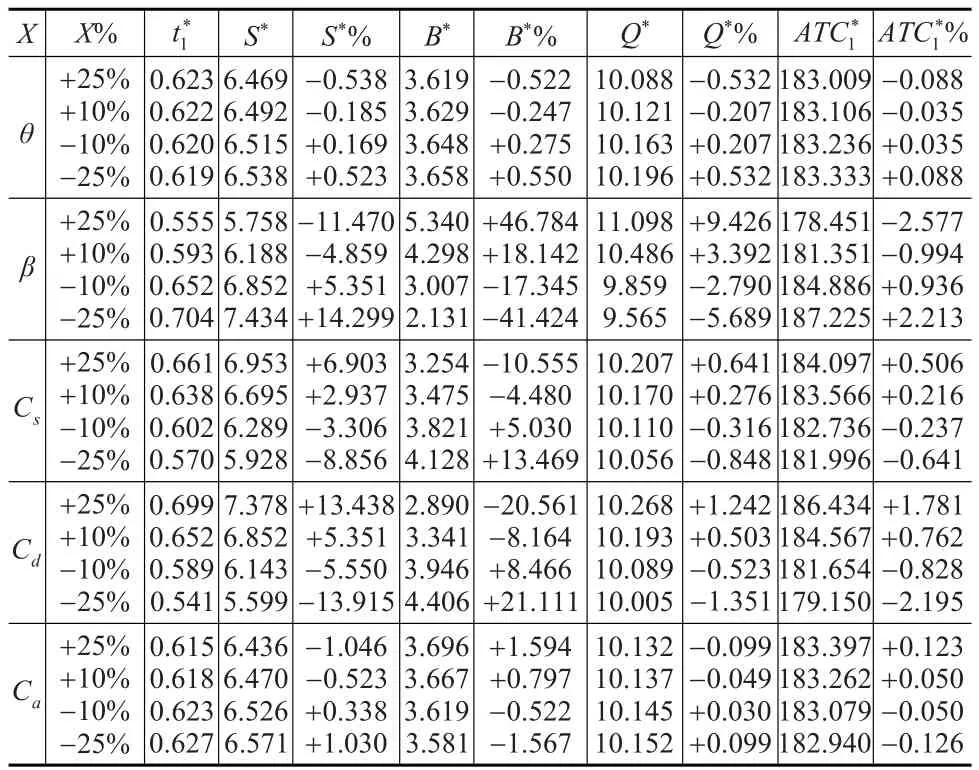
表1 0≤μ≤t1时的敏感性分析

从表1中的数据可以看出：（1）随着改良率θ递减，零库存时刻逐渐减小，最大库存水平S*、最大短缺量B*、最优订货数量Q*、最小单位时间总成本逐渐增大，且敏感程度表现为不敏感；（2）随着拖后率β递减，零库存时刻、最大库存水平S*、最小单位时间总成本逐渐增大，最大短缺量B*、最优订货数量Q*逐渐较小，且敏感程度介于稍敏感与极敏感之间；（3）随着单位缺货成本Cs递减，零库存时刻、最大库存水平S*、最优订货数量Q*、最小单位时间总成本逐渐减小，最大短缺量B*逐渐增大，且敏感程度介于不敏感与较敏感之间；（4）随着单位机会成本Cd递减，零库存时刻、最大库存水平S*、最优订货数量Q*、最小单位时间总成本逐渐减小，最大短缺量B*逐渐增大，且敏感程度介于不敏感与很敏感之间；（5）随着单位改良成本Ca递减，零库存时刻、最大库存水平S*、最优订货数量Q*逐渐增大，最大短缺量B*、最小单位时间总成本逐渐减小，且敏感程度表现为不敏感。

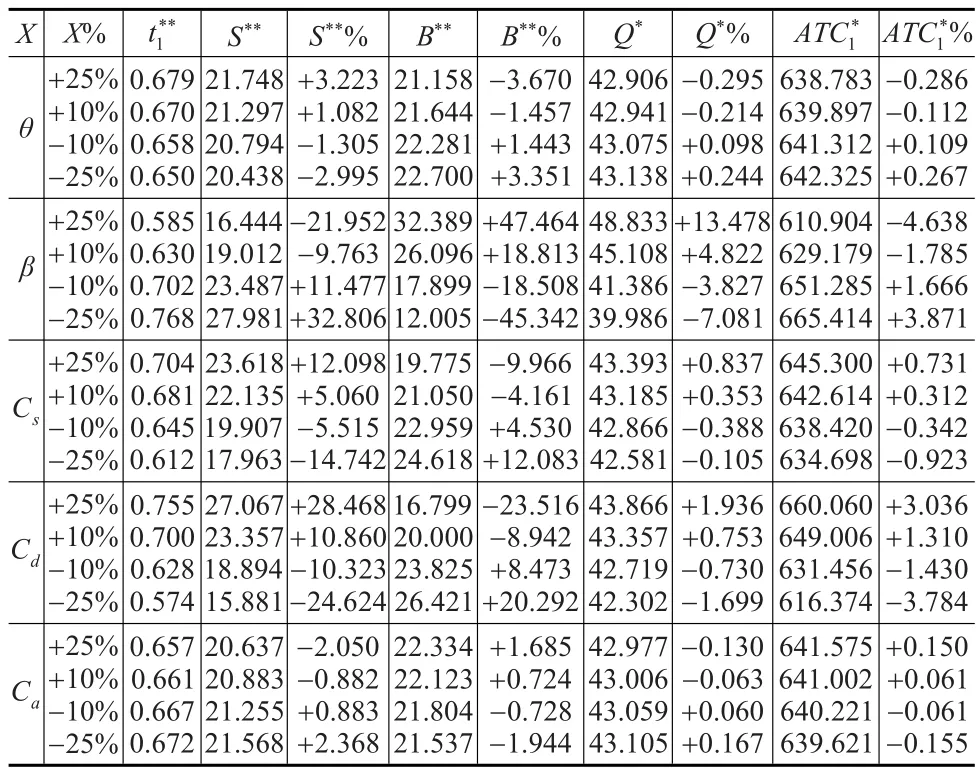
表2 t1≤μ≤T时的敏感性分析

从表2中的数据可以看出：（1）随着改良率θ递减，零库存时刻、最大库存水平S**逐渐减小，最大短缺量B**、最优订货数量Q**、最小单位时间总成本逐渐增大，且敏感程度介于不敏感与稍敏感之间；（2）随着拖后率β递减，零库存时刻、最大库存水平S**、最小单位时间总成本逐渐增大，最大短缺量B**、最优订货数量Q**逐渐较小，且敏感程度介于稍敏感与极敏感之间；（3）随着单位缺货成本Cs递减，零库存时刻、最大库存水平S**、最优订货数量Q**、最小单位时间总成本逐渐减小，最大短缺量B**逐渐增大，且敏感程度介于不敏感与较敏感之间；（4）随着单位机会成本Cd递减，零库存时刻、最大库存水平S**、最优订货数量Q**、最小单位时间总成本逐渐减小，最大短缺量B**逐渐增大，且敏感程度介于稍敏感与极敏感之间；（5）随着单位改良成本Ca递减，零库存时刻、最大库存水平S**、最优订货数量Q**逐渐增大，最大短缺量B**、最小单位时间总成本逐渐减小，且敏感程度表现为不敏感。

4 结论与展望

改良品是日常生活中常见的一类物品，但改良品的订货问题尚没有引起学者们足够的重视。本文在假设改良品的需求率服从斜坡型分布及改良率保持恒定的基础上，考虑允许缺货且短缺量部分拖后，根据需求拐点与零库存时刻出现的先后关系，分别建立不同情形下的零售商订货决策模型，给出数值算例模拟订货决策过程，通过敏感性分析探讨了模型部分参数变动对主要决策变量值的影响方式。

不同类型改良品在持有期间的改良率变化规律也会不同，现有文献中已见的有常数分布、两参数威布尔分布，及LOGISTIC分布。实际上，改良品在持有期间的改良状况往往比较复杂，以某一种分布来精确刻画是很困难的。本文的研究旨在讨论斜坡型需求下允许缺货的改良品库存问题，因此对改良率做了简单处理，仅以常数改良率为例。在后续的研究中，将进一步结合不同种类改良品的改良特征，搜集改良品持有期间的改良数据，拟合改良品的改良曲线，从而建立更具有实际可操作性的理论模型。