m叉平均树的差分隐私位置隐私保护方法

胡德敏,廖正佳

(上海理工大学 光电信息与计算机工程学院,上海 200093)

1 引 言

随着手持设备的日益普及,基于位置的应用程序和服务可以访问准确和实时的位置信息,在用户发送查询请求过程中难免会存在个人位置隐私泄露的问题.

许多基于k-匿名[1,2]置隐私保护方法已被证明不能充分保护LBS隐私,容易受到人口分布密度、背景知识攻击等影响.差分隐私[3,4]能使数据集的计算结果对元素的变化不敏感,因此由于数据集的加入而导致个别元素隐私泄露的风险被控制在可接受范围内.差分隐私具有坚实的数学基础;严格定义隐私保护并提供定量评估方法,逐渐成为LBS隐私保护领域的热门话题.但在连续的位置查询服务时,容易造成叠加噪声导致查询精度下降.

针对以上问题,本文在Hilbert曲线构建的k-匿名集的基础上,提出了基于m叉平均树的差分隐私位置隐私保护方法(m-Ary Average Tree Differential Privacy,MATDP).该方法通过引入m叉平均树结构拆分匿名集数据以增强数据效用,主要提出了经过严密推导得出的具有较小误差上界的拉普拉斯隐私预算分配策略.该隐私预算分配策略能有效控制连续查询环境下噪声叠加问题,在保证隐私保护强度的同时降低连续查询误差.实验结果表明,相较于其他位置隐私保护方法,该方法能在一定查询范围内减小连续查询误差,并且在同类提高查询精度的差分隐私算法中具有较高运行效率.

2 相关工作

位置隐私保护主要有三大方面:位置匿名、位置加密、位置扰动.

位置匿名被大量讨论和应用,k-匿名机制是位置匿名的典型代表.文献[5]提出的模型能支持具有上下文敏感的个性化隐私要求的广泛用户的位置k-匿名,从而使每个移动节点能够指定最低匿名等级以及最大时间和空间分辨率.但该匿名集中位置元素不满足互惠性[6],攻击者通过连续查询的匿名集求交后得到用户实际位置.文献[7]通过细化确定同一匿名集中移动用户的匿名空间是否相同,并且删除交集后的两个匿名空间是否为单一路径来保证互惠性.由于k-匿名机制容易受限于人口密度的分布,文献[8,9]以网格模式生成虚拟位置,同时考虑真实环境中的人口分布密度.总体而言,k-匿名有两个方面的制约因素,一方面匿名集中需要找代理用户与匿名服务器间的通讯[10]或用户间的对等协作,信任机制在这种模型中发挥着重的作用,信任的评估和量化变成一大挑战;另一方面k-匿名机制无法应对背景知识攻击,攻击者获得的背景知识是无法量化和建模的.因此单一的位置匿名方法隐私保护强度过低.

位置加密的密码学技术在位置隐私问题中得到了广泛的应用,隐私信息检索技术(PIR)[11],保证LSP在无法知晓查询内容和查询结果的同时完成查询工作.密码技术在定位隐私保护方面更为彻底和安全,理论上完全消除了攻击者的威胁,但密码学方法的缺点是计算复杂度高,对硬件要求较高.

差分隐私位置保护方法因其具有严格推理和证明的隐私保证,成为位置扰动中的一个常被应用的方法.在没有任何关于攻击者先前知识的假设情况下,地理不可区分[12]使用差分隐私来扰乱真正的用户位置.在LBS应用中,连续查询环境时噪声会累加到每次查询上,产生的噪声量会影响查询精度和数据的可用性.如何在隐私保护和查询精度之间获得较好的权衡,是学者们一直在努力的方向.文献[13]基于小波变换的差分隐私方法,该方法把数据映射成小波树后添加噪声,但映射成小波树后会出现大量为零的值需要进一步压缩,增加了算法复杂度.文献[14]提出PriLocation模型,将实际位置划分到k个集合中,统计集合的访问频次,再对k个集合添加噪声,由于集合数一定小于单个位置数量,所以噪声的添加会减少,但实际查询准确率不高.文献[15,16]提出了将树结构加入差分隐私的方法,缺点是划分不稳定会造成划分结构不均匀的情况.文献[17]通过迭代的方式往树的层次中添加噪声,虽然降低了查询误差,然而在有些层次中不满足一致性约束[18].如何设计一个适合于移动设备在连续查询环境下的位置隐私保护方法,是本文要解决的关键问题.

单一的k-匿名机制,由于缺乏抵抗背景知识攻击的能力,需要与其他位置隐私保护方法结合使用.从另一角度来看,若仅使用差分隐私位置保护方法扰动单个位置,依据定义可知,LSP查询数据集时会导致对单个记录的变化敏感度较低,使得LBS服务没有意义[26].差分隐私更适用于对数据集信息的扰动,因此本文将k-匿名机制与差分隐私技术相结合.

对于当前差分隐私位置保护方法中存在的噪声累加导致查询精度过低的情况,本文在Hilbert曲线划分的k-匿名机制基础上,提出基于m叉平均树的差分隐私位置隐私保护方法.该方法使用m叉平均树结构来拆分数据以增强数据效用,并经过严格数学推导,使得隐私预算的分配存在较小噪声方差上界,在相同的隐私水平下提高了数据查询的准确性和数据效用.

3 相关概念

差分隐私

差分隐私保证数据的发布结果不会因任何特定个体的存在而发生显着变化.对于数据是数值类的情况,最普遍的机制是将从拉普拉斯分布中抽取的受控随机噪声添加到查询输出中.噪音量与随机函数的灵敏度相关联.

定义1.ε-差分隐私.对于任何两个数据集D和D′,至多包含一个不同的记录,对任意输出S⊆Range(f)满足:

Pr[f(D)∈S]≤eε×Pr[f(D′)∈S]

则算法f满足ε-差分隐私.

隐私预算ε影响隐私保护程度,ε越小,f(D)与f(D′)的概率密度函数相似度越大,隐私强度也越大,数据可用性降低(即查询精度降低).本文目标是通过对隐私预算ε的合理分配,谋求在隐私保护强度与查询精度之间的平衡.

Δf为f的敏感度,是数据集D中任何单个元组变化时f中的最大变化,即:

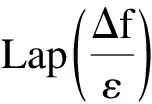
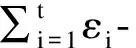
根据定义3可知,同一数据集下多个差分隐私的组合会导致隐私参数ε和方差的累加.因此,在连续查询情况下,每个兴趣点噪声的累加的确会带来较大的查询误差.

4 基于m叉平均树的差分隐私位置隐私保护方法

4.1 整体框架

本文提出的位置隐私保护架构由客户端、匿名服务器(Anonymous Server,AS)和位置服务提供商(Location Service Provider,LSP)组成,如图1所示.

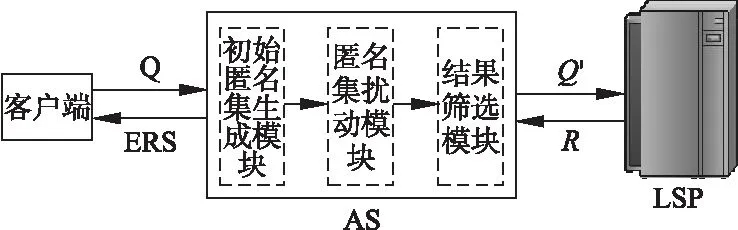
图1 整体框架图Fig.1 Overall framework

1)客户端.客户发送实时查询请求Q=(分别表示用户身份信息,用户真实位置,查询内容以及时间戳)给AS进行匿名操作.

2)匿名服务器AS.出于对移动客户端的计算能力和存储负载的考虑,引入匿名服务器进行匿名操作.匿名服务器能实现大规模计算,处理大量用户频繁的位置更新操作(特别是在连续查询环境中)以及细化查询结果.缺点是匿名服务器掌握了移动用户相关的位置信息,成为系统处理的瓶颈,攻击时会导致用户隐私泄露.出于对系统安全性考虑,要求AS掌握查询请求中的loc数据,而无法获知真实的查询内容(防止背景知识攻击).

3)位置服务提供商LSP.LSP负责处理查询,仅掌握content数据以及扰动后的匿名空间区域(Anonymous Space Region,ASR)数据,无法获知相关身份信息.完成查询操作后,将候选结果集R发送给AS.

具体步骤如下:

1)用户将查询请求Q=发送给AS.

2)AS获取Q中的位置信息loc,利用初始匿名集生成模块生成初始k-匿名集;匿名集扰动模块利用m叉平均树差分隐私保护方法对k-匿名集中的兴趣点进行扰动,最终生成ASR.将扰动后的查询请求Q′发送给LSP.

3)LSP获取Q′中的查询信息content以及ASR,完成查询操作后返回给AS候选结果集R.

4)AS利用结果筛选模块筛选出精确结果集(Exact Result Set,ERS),返回给客户端.

4.2 生成初始k-匿名集

使用基于密度划分的Hilbert曲线[21,22]将兴趣点映射到一维.Hilbert曲线的优势是,在将二维空间数据映射到一维时,在二维空间上邻近的点在Hilbert曲线上依然保持邻近.考虑到兴趣点分布密度的因素,首先对区域进行四分树划分,使每个单元内的兴趣点个数不大于阈值δ,如图2所示(图中设δ=1);其次将兴趣点依据Hilbert值(H值)从小到大排序;最后,为了满足匿名集的互惠性,将排序后的兴趣点基于桶的划分得到k-匿名集.

定义4.互惠性[6].相同匿名集中的任意两个元素a1,a2,若a1,a2分别构造的匿名集Sa1,Sa2,满足Sa1=Sa2,则称此匿名集具有互惠性.

图2 基于密度划分的Hilbert曲线Fig.2 Hilbert curve based on density division

例如,图2中离用户实际位置最近的兴趣点为P9,若k=3,Hilbert曲线填充后,兴趣点依据从小到大排序并基于桶的划分后得到:

P1,P2,P7P8,P9,P4P5,P6,P10P13,P15,P12P11,P14,P3

P9所在匿名集为,阴影部分为匿名区域.从图中可以看出形成的匿名区域较大(包含的单元格较多,后期噪声累加后会产生较大的查询误差),需要进一步优化.

为了优化Hilbert曲线生成的匿名区域.通过改变曲线的起始点和方向,生成多种Hilbert曲线(本文只考虑8种Hilbert曲线,即4种起始点×2种方向),筛选出匿名区域最优的匿名集作为最终的匿名集.如图3所示,由该Hilbert曲线获得的匿名区域明显优于原始曲线生成的匿名区.

4.3 匿名集的差分扰动

本文用提出基于m叉平均树的差分隐私方法,对形成的初始匿名集添加拉普拉斯噪声扰动.通过引入m叉平均树的数据结构,推导出具有较小误差上界的隐私预算分配方法降低噪声.

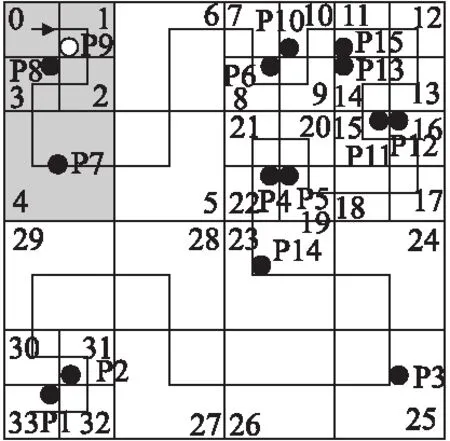
图3 改变后的Hilbert曲线Fig.3 Changed Hilbert curve

4.3.1 构建M叉平均树

定义5.广义敏感度[23].设有函数集F,其中f∈F,W为f的权重函数,函数f关于权重函数W的广义敏感度为满足以下式子中ρ的最小值:

∑f∈F(W(f)·|f(D)-f(D′)|)≤ρ·‖D-D′‖1

(1)

其中‖D-D′‖1=∑v∈D-D′|v|.

定义6.函数f关于权重函数W的广义敏感度为ρ,若算法A在数据集D的输出为{f(D)+X(f)},其中X(f)服从拉普拉斯分布λ/W(f)的随机噪声,那么算法A满足(2ρ/λ)-差分隐私.

定义7.m叉平均树.m叉平均树中,除叶子节点以外,每个节点有m个孩子,内部节点的值为其孩子节点的平均值.

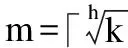
例如,当匿名集中兴趣点个数为7(以图3中Hilbert曲线值为例),给定高度h的值为3,则m=2,生成的平均树如图4.

图4 m叉平均树Fig.4 M-ary average tree

根据公式(1)和权重函数W(f)=mi计算出m叉平均数的广义敏感度.设匿名集D上的元素值被改变了δ,则其叶节点及该叶节点的祖先节点也会被改变,共有h+1个节点值被改变,深度为i的节点被改变的大小为δ/mi,将此代入公式(1),得到关于权重函数的广义敏感度为:

4.3.2 隐私预算分配

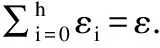
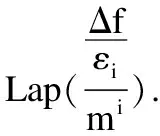
4.3.3 查询误差上界推导

本文用方差E(Q)表示查询请求Q的误差度量.由定义3可知,噪声是在每个节点添加的,由此产生的误差为每层产生的方差之和,即:

(2)

根据柯西不等式,

(3)

通过整理可得:

(4)

将公式(4)代入公式(3)得到:

(5)

由此得到了每层节点需要添加噪声的隐私参数εi.

因为查询误差:

由式(5)可以得出误差的最大值:

基于m叉平均树的差分隐私位置保护方法的整体算法如下:

算法.基于m叉平均树的差分隐私位置保护算法

输入:用户u所在的二维空间G,阈值δ,匿名集参数k

输出:扰动后的匿名区域ASR,匿名集u.s

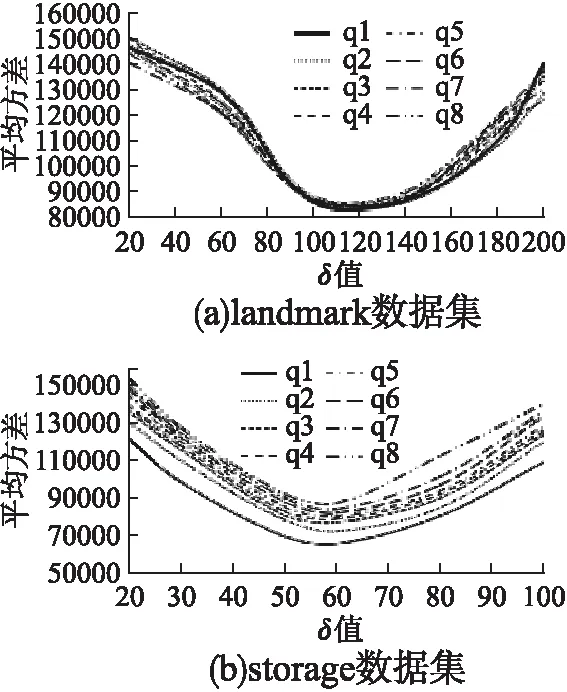
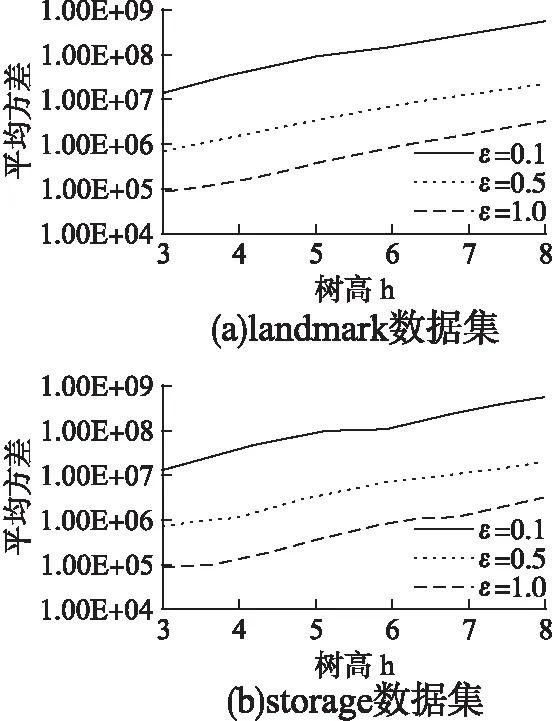
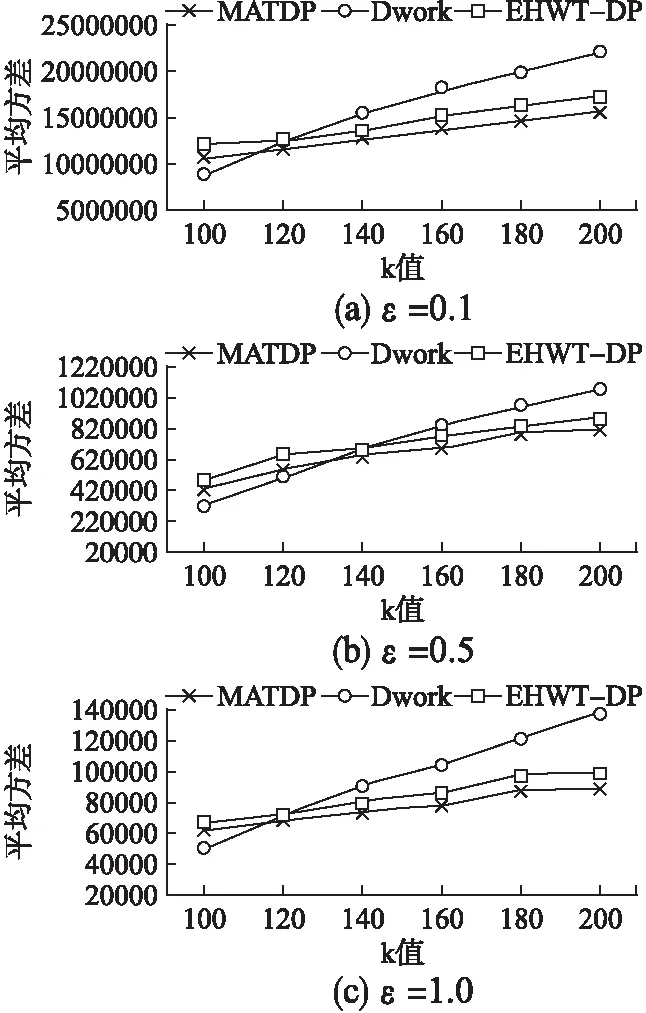
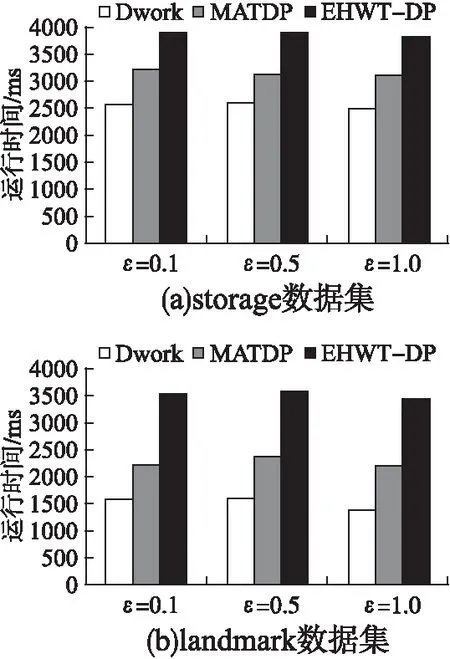
1.if(G.POI.count

2.return ERROR;

3.else

4.G划分为4个子区域Gi;

5.for i=1 to 4

6.if(Gi.POI.count>δ)

7.do step 4;

8.else 结束区域G的划分;

9.end for

10.end else

11.end if

12.G中填充Hilbert曲线;

13.order(H(G.POI));//将兴趣点的Hilbert值排序

14.基于桶的划分k-匿名集;

15.ASR=Area(u.s);//记录下u所在的匿名集形成匿名区域

16.for i=1 to 8

17.改变Hilbert曲线的起始点或方向;

18.do step 13 to 15;

19.if(Area(u.s′)

20.ASR=Area(u.s′);

21.u.s=u.s′;u.s′=NULL;//保留当前匿名集和匿名区域

22.end if

23.end for

26.将平均树中前u.s.count个叶子节点的值依次赋给u.s中的每个元素.

5 实验结果与分析

本文针对查询误差和算法运行效率对MATDP算法进行对比分析.基于Hilbert曲线生成匿名集的部分,在匿名服务器离线状态下生成,即离线状态下根据既定的阈值δ划分网格,填充8种Hilbert曲线,并按H值的大小排序兴趣点.影响查询误差的因素有很多方面,如网格划分阈值δ、匿名集规模k、匿名区域大小、树高h、隐私预算ε以及兴趣点分布密度等.因此实验不仅从以上几个因素测试,也要与其他算法比较该算法的查询误差和运行效率.

5.1 实验数据与环境

实验环境为Inter®CoreTMi5,windows7操作系统,8GB内存,算法是Eclipse环境下基于Java编写.

实验选择两个数据集进行,第一个数据集为infochimps大数据网站提供的美国48个大陆州的地标位置组成的地标,实验中简称为“landmark” 数据集,数据分布较密集,约有870k个数据点.第二数据集为美国存储设施位置数据,包括国家连锁存储设施,以及本地拥有和运营的设施,数据集较小,约有9000个数据点,简称为“storage”数据.两个数据集的密度和稀疏度是显而易见的,因此可以用这两个数据集来验证本文的方法对不同密度环境因素的影响.

实验中将平均方差作为查询误差的衡量标准:

其中q(D)为真实位置的查询结果,q(D′)为加噪后的查询结果,|Q|为匿名集大小.用移动对象生成器[25],生成速度为30km/h的300个移动用户,设查询总时间为30min,查询间隔为5min,因此所有用户一共要发起1800次的连续查询.

5.2 网格划分阈值δ在不同匿名区大小中对查询误差的影响

该实验中取k=180,ε=1,h=3.比较不同密度环境下δ对查询误差的影响(实验中δ的最小取值要使得最小单元格不小于1km2).q1～q8为8种Hilbert曲线形成的匿名区域从小到大的排序.

从图5(a)可知,在密度较大的landmark数据集中对于同一δ值,q1～q8的误差波动幅度不大,基本相似.在图5(b)storage数据集中,同一个δ值q1～q8的误差呈逐渐递增趋势,匿名区面积较小的误差值较小.这是因为较密环境中由于k值一定,不同Hilbert曲线所包含的单元格数相近,噪声叠加后误差也基本相似;而在稀疏环境中,k值一定时,匿名区越小的Hilbert曲线所包含的单元格也较少,误差也越小.因此在密集环境中,k值一定时无论哪种Hilbert曲线,误差影响都不大;稀疏环境中,k值一定时要选择形成匿名区面积较小的Hilbert曲线.

图5 阈值δ对查询误差的影响Fig.5 Influence of threshold δ on query error

比较图5(a)和图5(b)两图,δ取值极小和极大时,误差都较大,δ取值较为适中时误差最小,且密集环境中的最优阈值大于稀疏环境的最优阈值.这是因为δ过小,划分的单元格就越细,较多的单元格会使噪声叠加较多;反之δ过大,查询精度不够也会造成误差过大,所以较适中的δ值会降低查询误差.

5.3 树高h对查询误差的影响

该实验取k=180,根据上节的结论,landmark数据集取δ=100,storage数据集取δ=60,取q1为匿名区域(密集环境q1～q8误差相差甚小,无论哪个匿名区都可以;稀疏环境q1的误差最小,所以综合选择q1为匿名区).

比较图6(a)和图6(b)两图,不同h在landmark和storage数据集中平均方差相似,表示树高对不同密度环境的影响较小.随着隐私预算ε增大,误差越小.随着树高h的增加,误差逐渐增加并呈指数函数增长,这是因为误差公式E(Q)与树高h呈指数关系,并且分配较小的h具有较低的误差.

图6 树高h对查询误差的影响Fig.6 Influence of tree height h on query error

5.4 匿名集规模k在不同隐私预算下对查询误差的影响

该实验只在landmark数据集中比较,因为storage数据集太小而无法从中受益.同时,引入差分隐私最基本的算法(称Dwork算法)以及对提高差分隐私查询精度有代表性的哈尔小波零树压缩算法(称EHWT-DP算法),与本文MATDP算法进行误差的比较.根据前两节的实验结论,该实验取δ=100,h=3,匿名区q1.

图7中整体看得出,MATDP算法误差在ε=0.1时要比ε=1时高出102倍.当k值较小时,Dwork算法误差要小于其他两种算法.但随着k值增大(查询范围也逐渐增大),Dwork算法误差呈线性累加地增大,MATDP算法的误差较小,且与EHWT-DP算法相比较具有更低的查询误差.同时,在图中可看出,MATDP算法误差虽然随着查询范围的增加而增加,但会逐渐趋于稳定,这是由于该算法的隐私预算分配有误差上界.

5.5 算法运行效率

该实验分别对landmark数据集取δ=100,storage数据集取δ=60,同时h=3,k=180,匿名区q1(该数据的选取参考上述实验结论),分别在不同ε值下比较三种算法的运行效率.

图7 匿名集规模k对查询误差的影响Fig.7 Impact of anonymous set size k on query error

由图8可知,在相同数据集下不同的ε值每种算法的运行时间基本相同,表示隐私预算ε不影响算法效率.Dwork算法运行时间最短,其次MATDP算法相较于EHWT-DP算法运行效率较高.是因为EHWT-DP算法对数据转换成小波树的形式后还需将数据压缩,再添加噪声,算法复杂度为O(klogk),而MATDP算法复杂度为O(k).整体来看,storage数据集下三种算法运行效率高于landmark数据集,这是由于δ值和k值一定时,较密环境生成的匿名区面积整体要小于稀疏环境的匿名区,查询时速度较快.

图8 算法运行效率Fig.8 Algorithm operating efficiency

6 结束语

基于位置的服务给生活带便利的同时位置隐私问题也是不容小觑.本文在Hilbert曲线构建的满足相互性的k匿名集基础上,通过改进原始差分隐私方法在连续查询下噪声过大的问题,提出了基于m叉平均树的差分隐私保护方法,该方法使用m叉平均树结构拆分匿名集数据以增强数据效用,并通过严密推导出具有较小误差上界的拉普拉斯隐私预算分配策略.从阈值δ、匿名集规模k、匿名区域大小、树高h、隐私预算ε以及兴趣点分布密度等方面测试了算法对误差的影响.并且与同类提高查询精度的差分隐私方法相比,具有高效的运行效率.但在较小范围中,查询精度不太高,在未来的研究中,还要致力于在小范围中对算法查询精度的提高.