基于贝叶斯-Copula模型的突发堆载下盾构隧道结构安全性评价

王丙苗， 陈三强， 刘文黎， 陈世杰， 韩 鹏， 李 黎， 同一村

(1. 武汉地铁运营有限公司， 湖北 武汉 430030； 2. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

近十年来，城市轨道交通以其施工便捷、快速及对环境影响小等优点得到快速发展，如今渐渐形成了以地铁为轴线的交通网络，但伴随着大量的临近施工活动(如堆载、基坑施工等)，可能对地铁的正常运营带来明显的影响。邻近工程活动会对临近的运营盾构地铁结构带来许多安全隐患(如渗漏水、管片开裂、道床脱开等病害)，以及结构使用性能的降低风险。

目前已有部分关于临近活动对盾构地铁结构影响的分析成果。邵华等[1]分析堆载引起的盾构隧道变形及病害特征，并对卸载及综合加固整治措施及效果进行分析。Zhang等[2]研究周围深基坑开挖对地铁的影响。何川等[3]探讨和揭示围岩条件、隧道净距、顶推力等因素对已建平行隧道的变形和附加内力分布变化规律的影响。贺美德[4]等分析浅埋暗挖(Cross Diaphragm，CRD)法上穿盾构隧道施工，分别对隧道结构竖向位移、隧道结构水平收敛位移及道床结构竖向位移3种变形的影响。Yamamoto等[5]分析了堆载对既有地铁的影响。王如路等[6]提出了以隧道直径变化作为隧道横向结构性态发展的判定指标。这些研究主要分析周围活动对地铁的变形、受力规律等因素的影响，缺少运营地铁结构安全的评估研究。

国内外研究学者通常采用基于定性评价方法(如事故树分析、影响图法等)识别地铁结构的安全状态，然而这些方法参数属性区间划分和权重设置存在较大的主观判断，基于此，本文采用结构可靠度分析这个定量评估方法。传统的系统可靠性分析通常假设系统部件和各组成单元之间相互独立，其分析结果往往将多种失效模式进行失效概率叠加，然而在地铁运营安全可靠性评价中，系统出现故障的致险因素非常复杂，且相互之间存在复杂的时间耦合交互作用关系，本文采用Copula理论实现参数失效模式的相依性叠加。另外，由于地铁周围的临近活动具有明显的时效性，传统的安全评价往往局限于静态过程的推理，难以反映时空变化对地铁运营安全风险演化的实时影响。故而本文采用贝叶斯更新理论，考虑时变效应下临近环境变化对地铁结构安全的影响，建立较为精确的运营地铁安全状态评价模型。

参考相关文献资料，首先选取评价地铁结构安全可靠性的指标参数；再采用不同的Copula函数构建这两个参数的相依性模型，并通过AIC(Akaike Information Criterion)和BIC(Bayesian Information Criterion)准则识别出最优的Copula模型；然后，基于Weibull分布的Frank Copula可靠性模型构建，结合贝叶斯统计推断理论和马尔科夫链蒙特卡洛(Markov Chain Monte Carlo，MCMC)以及Metropolis-Hastings算法抽样技术，对指标的边缘分布和相依型联合分布函数进行参数估计与统计推断，得到参数的后验分布和相关统计量，从而实现评价模型的实时更新，得到Copula二元离散时变相依模型；最后，以武汉地铁2号线某段区间为工程背景，利用Copula函数构建指标的二元联合分布函数模型，从而在考虑指标因素之间相依性的情况下，采用蒙特卡洛模拟法，得出该段地铁工程的安全可靠度。通过运营地铁结构的相依性建模及安全可靠度评价，能够更准确和全面地捕捉到数据中蕴含的信息，实现运营地铁结构安全性的准确评价，为运营地铁的安全管控提供更精准的信息支持。

1 贝叶斯Copula相依性建模理论

1.1 基于Copula理论的相依性模型原理

Copula方法基于Sklar定理[7]：设F(x1，x2，…，xn)为边缘分布函数的联合分布函数F(x1)，F(x2)，…，F(xn)，存在对于n维Copula，x1，x2，…，xn有：

F(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]

(1)

式中：C为F(x1),F(x2),…,F(xn)的Copula函数。

Sklar定理将多维参数联合分布的构建过程分为两个步骤：(1)从样本数据估计边缘分布的统计参数；(2)最优Copula函数识别。根据Sklar定理，两个随机变量x1，x2的两参数联合分布如下：

F(x1,x2)=C(F1(x1),F2(x2),θ)=C(u1,u2,θ)

(2)

式中：u1,u2为Copula函数中的边缘分布函数，θ为x1，x2之间的相关性测度。

(1)Copula函数的类型

本文选择的Copula函数如表1所示。其中，Gaussian为椭圆族Copula函数，Clayton，Gumbel，Frank Copulas为常用的阿基米德Copula函数。

表1 本文采用的Copula函数类型

注：Φρ为相关系数矩阵为ρ的标准正态分布函数

(2)Copula函数参数θ的估计

Copula参数θ可以通过Pearson线性相关系数或秩相关系数来确定[8]。由于Pearson系数在线性条件下能保持不变，但在非线性条件下不稳定，故而本文采用Kendall秩相关τk来确定Copula参数。τk可以度量两个随机变量的依赖性程度，对于具有N个值的两变量x1，x2的非参数估计τk可以由式(3)计算：

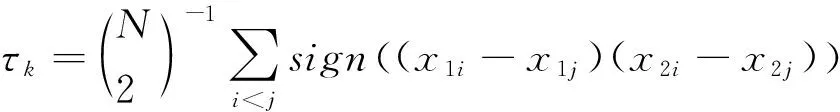
(3)

这里，sign(·)定义为：

(4)

根据Copula理论，τk可以用Copula函数表示：

(5)

因此，与给定的Copula函数相关联的Copula参数θ可以通过求解上述积分方程来确定。

(3)最优Copula函数识别

在确定Copula参数θ之后，可以唯一地得到Copula联合分布函数和Copula联合概率密度分布函数。然后，可以使用Akaike信息准则AIC和贝叶斯信息准则BIC的计算值区分识别最优Copula函数，公式如下：

(6)

(7)

(8)

式中：k为Copula参数的数量，本文中k值为1；N为相关数据的样本大小。当AIC和BIC取值最小时所对应的Copula函数为最优Copula函数。

1.2 贝叶斯推断理论

一个典型的贝叶斯分析通常由三个主要过程组成[9]：(1)一个能刻画所有变量包括样本数据、缺失数据和未知参数关系的全概率模型即联合分布；(2)用适当的后验分布对未知参数进行描述；(3)所用模型的评价与选择。联合概率分布可表示为联合概率分布参数θ的似然函数X参数的先验分布，即

p(y,θ)=p(y|θ)f0(θ)

(9)

利用贝叶斯定理

(10)

获得参数的后验分布完成步骤2。当参数θ为离散时，积分符号用求和符号替代。

分母P(y)看成常数，在实际中，求P(y)的值很不容易，但通常用马尔可夫蒙特卡罗方法估计。假设参数向量不止一个分量，如θ=(θ1，θ[-1])，其中θ[-1]为除第一个分量处的所有分量组成的向量。可对多余参数向量θ[-1]积分剔除得到参数θ1，即

(11)

1.3 马尔可夫链蒙特卡罗(MCMC)方法

选择通过运行一个以π为稳定分布的马尔可夫链来产生相关样本，此方法称为马尔可夫链蒙特卡罗(MCMC)方法，Metropolis等首先提出具有非常一般性的产生马尔可夫链的方法，假设马尔可夫链是不可约的、非周期并且收敛到唯一的平稳分布π(x)，则每个马尔可夫链蒙特卡罗计算的实质就是对某一给定函数h(·)的均值Eπh(x)的估计。在过去的几十年中此方法受到广大学者充分的重视从而迅猛发展[9,10]。抽样方法有重点抽样、Metropolis抽样、Metropolis-Hastings抽样、随机游走Metropolis抽样和Gibbs抽样算法。本文采用Metropolis-Hastings抽样算法。

(12)

1.4 MCMC收敛诊断

根据马尔可夫链的遍历性，所有基于MCMC的统计推断都是在假定Markov链已经收敛的条件下进行的。所以MCMC的收敛性诊断对于用参数的后验估计有重要影响。目前MCMC收敛诊断的方法很多，本节主要介绍应用最广泛的G-R(Gelman-Rubin)收敛诊断方法。MCMC收敛诊断方法基于用正态分布近似目标分布π的理论，主要由以下几步构成[9]：

(1)开始抽样之前，找一个简单的分布f(x)，该分布相对于目标分布而言是过度扩散的，并且从f(x)中产生m个独立同分布样本；

(2)将得到的m个独立同分布样本作为抽样的初始状态，开始m个独立抽样，让每条链运行2n次迭代；

(3)每条链分别迭代2n次，将前n次“退火”舍弃，将其记为xij,i=1,2,…,m，j=1,2,…,n；然后利用余下的n次迭代结果xij，计算m条链内方差的平均值W和m条平行链均值间的方差B，即

(13)

(14)

2 工程背景

武汉地铁长港路—汉口火车站区间始于长港路站南端，横穿常青三路、红旗渠路、汉丹铁路、常青一路后向南进入汉口火车站站场到汉口火车站北端止。2016年3月份该区间隧道在DK3+750—DK3+945段地面有面积堆土，堆土高出原设计标高(21.8 m)6 m多，导致运营地铁管片出现大规模病害(如：裂缝、渗漏水、道床脱空等)，给地铁结构的正常运营带来了巨大隐患。

本区间自上而下地层依次为1-1填土层、3-1粘土层、3-3层淤泥质粉质粘土，3-4层淤泥质粉质粘土夹粉土、粉砂，3-5层粉质粘土、粉土、粉砂互层，4-1层粉细砂，4-2层细砂。区间隧道主要穿越3-3层淤泥质粉质粘土，3-4层淤泥质粉质粘土夹粉土、粉砂，局部穿越承压水层，承压水主要位于3-5粉质粘土、粉土、粉砂互层，4-1粉细砂层，4-2细砂层，水位标高约为地面以下2.2～3.5 m。其土质分布图如图1所示。

图1 长港路—汉口火车站区间土质分布

此工程中，隧道管片在地表堆土荷载的作用下，出现了明显的病害特征，如图2，主要体现在：(1)隧道出现最大超过100 mm的净空收敛。拱顶收敛-105 mm，水平收敛最大值为+91 mm，左线在ZDK3+900处(384环)，右线在YDK3+900处(399环)。(2)隧道出现了最大约为1‰的差异沉降。左线2016年3月以来沉降较明显为ZDK3+680.505—ZDK3+945，隧道差异沉降最大区段为ZDK4+227—ZDK4+254.085，左线隧道最大差异沉降为0.98‰<1.6‰～2‰。右线2016年3月以来沉降较明显为YDK3+714—YDK3+946，隧道差异沉降最大区段为YDK3+785—YDK3+819，右线隧道最大差异沉降为1.02‰<1.6‰～2‰。

图2 堆载区运营地铁病害情况

3 基于Copula函数和贝叶斯更新的地铁运营安全时变可靠性分析

参考同济大学黄宏伟教授对上海某地铁区间突发堆载问题的研究成果[1,11,12]，选取净空收敛(Convergence Deformadon，CD)和差异沉降(Differential Settlement，DS)作为评价地铁结构安全可靠性的指标，并采用该堆载段监测得到的净空收敛和差异沉降数据作为构建贝叶斯更新的Copula函数模型的数据来源。构建两变量参数的相依性模型时，参数的边缘分布常常选用相同的分布函数类型，并用极大似然法来估计两参数的相关系数。

3.1 最优Copula函数参数相依性建模

(1)最优边缘分布拟合函数的识别和选择

在Copula理论框架下构造变量的联合分布函数可以分两步进行：1)选择估计变量的边缘分布拟合函数；2)选择识别最优的Copula函数。为了较好地识别出最优的边缘分布函数，选取AIC和BIC准则对监测得到的收敛和沉降值进行检验，从而分析得出最优的边缘分布函数对原监测数据进行拟合。表2给出了收敛和沉降监测数据的各种统计量。

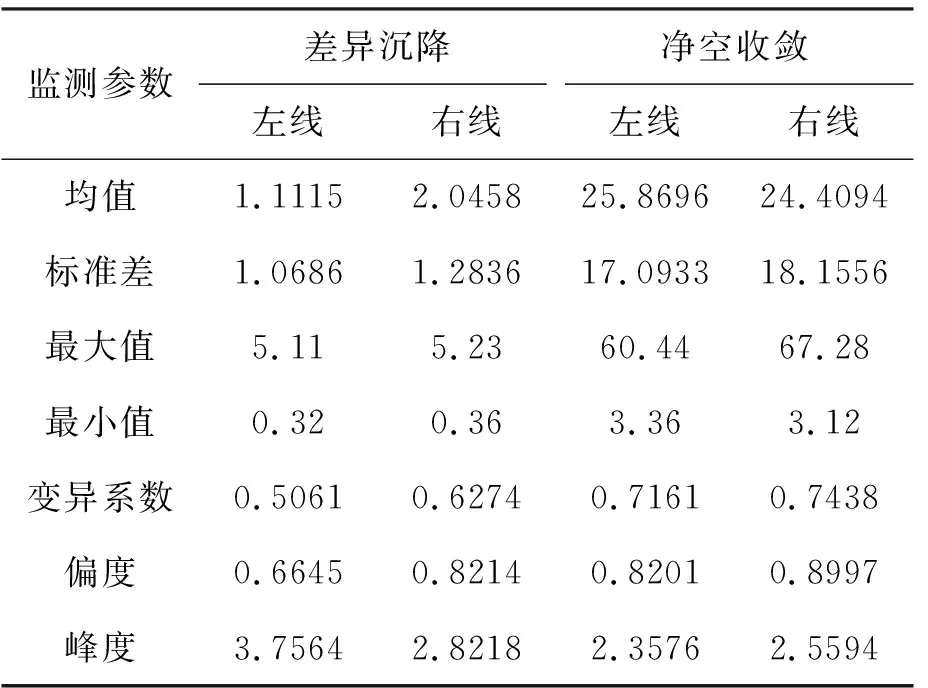
表2 监测参数的统计量 mm

选用AIC和BIC准则对备选边缘函数进行最优边缘分布函数检验，如表3。根据AIC和BIC准则，AIC和BIC值最小的威布尔分布函数为最优边缘分布函数，从表中发现，Gamma分布的拟合效果与Weibull分布较为接近，其次是正态分布，而指数分布的拟合效果最差。

表3 AIC和BIC准则的最优边缘分布函数检验

(2)最优Copula函数的识别和选择

基于自动化监测系统采集的盾构地铁结构左右线的净空收敛(CD)和差异沉降(DS)监测数据作为原始数据，左右线地铁监测截面的净空收敛和差异沉降之间Peason及Kendall秩相关系数，采用Kendall秩相关系数能对Copula函数的相关参数进行非参数估计，可得Clayton，Gaussian，Gumbel，Frank 等Copula函数的相关参数，如表4所示。

计算左右线净空收敛和差异沉降的不同Copula函数的AIC和BIC准则计算值，并选择具有最小AIC和BIC值的Copula函数作为拟合参数净空收敛和差异沉降间相关结构最优的Copula函数，结果见表4。由表4可知，AIC和BIC计算值由小到大依次是Frank、Gumbel、Clayton和Gaussian Copula函数，Frank Copula函数具有最小的AIC和BIC值，是通过AIC和BIC准则识别出来的最优Copula函数。而Gaussian Copula函数的AIC和BIC准则计算值较其他三个阿基米德族Copula函数计算值大很多，说明其拟合效果较差，表明左右线的净空收敛值和差异沉降值呈现非正态的相依结构。

表4 Copula函数相关参数计算结果

为更直观比较不同Copula函数之间的差异，给出了四种不同的Copula函数的模拟结果，如图3所示。

图3 不同Copula函数模拟散点图

3.2 二元Weibull分布的Frank模型时变更新

选取该堆载段监测得到的CD和DS数据作为构建贝叶斯更新的Copula函数模型的数据来源。首先以2016年4月1日—2016年5月30日的原始CD和DS监测数据作为样本数据进行参数估计，假设CD和DS分别属于Weibull{λ1,κ1}和Weibull{λ2,κ2}分布。得到左线Weibull分布参数θ,λ1，λ2，κ1，κ2的均值，分别为θ=3.377，λ1=2.381，κ1=2.105，λ2=26.567，κ2=1.491，这些参数的先验分布统计值见表5所示。再分别采用Weibull和Gamma分布来拟合这些参数，得到其边缘分布函数，发现Weibull分布的拟合效果较好，假定相依参数θ～N(μ,σ2)，参数λ1,λ2,κ1,κ2的先验分布为Weibull分布，同时假定它们之间相互独立，即λi～Weibull(ai,bi)，κi～Weibull(ci,di)，i=1, 2。拟合得到超参数的取值，即a1=28.25，b1=56.12，a2=15.85，b2=83.25，c1=27.51，d1=52.28，c2=16.25，d2=86.57。

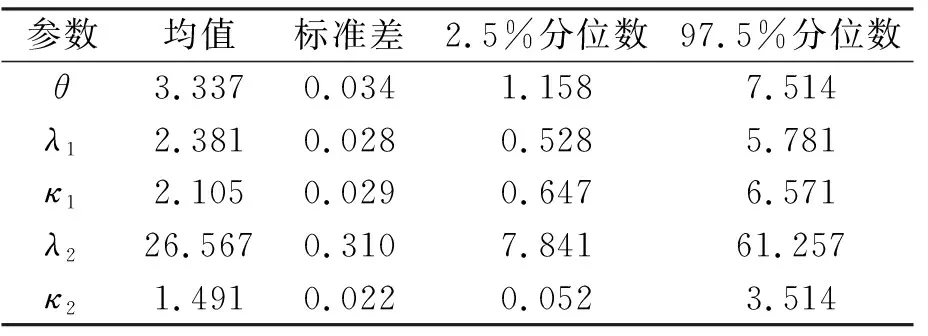
表5 参数的先验分布统计值

采用MCMC抽样算法，产生5条Markov链，从Weibull边缘分布函数以及参数θ=3.377的FrankCopula模型抽样10000个样本，对前5000个样本进行“舍弃”，利用每条链的后5000个抽样样本进行模拟分析，图4为MCMC抽样第1和第5条链参数的后验密度图。

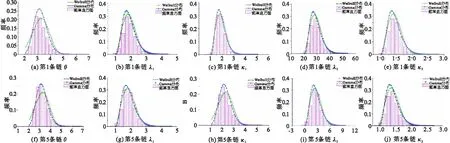
图4 各参数的后验概率密度图

图4中分别采用Weibull和Gamma分布函数进行拟合，发现Weibull分布的拟合效果更好，这样验证了选用Weibull分布作为拟合各参数的准确性和合理性。对比第1条链和第5条链各参数的后验概率密度图发现，两条MCMC仿真得出的数据相似度较高，表明本文构建的MCMC仿真的收敛性和稳定性。图5给出第1和5条链各参数的动态轨迹图，发现除去较少的奇异点外，Markov链数据基本平稳，且两条链上各参数的取值大致相同。从这两条链的迭代轨迹图可知，迭代的Markov链收敛，MCMC仿真过程是平稳的。

图5 各参数的动态轨迹

通过“退火”舍弃5000样本量，从5条链的动态轨迹图可以知道每条链收敛，对每条链的后5000个样本进行统计分析，得出参数估计的均值、标准差和95%的置信区间如表6所示。对比表5，6可知，参数先验分布和后验分布的均值大致相同，但后验分布的参数标准差小于先验分布标准差，θ的标准差从0.034减少到0.029，减少14.7%；λ1的标准差从0.028减少到0.021，减少25.0%；κ1的标准差从0.029减少到0.022，减少24.1%；λ2的标准差从0.310减少到0.256，减少17.4%；κ2的标准差从0.022减少到0.018，减少18.2%，说明模型参数经过贝叶斯更新后，参数的不确定性降低。

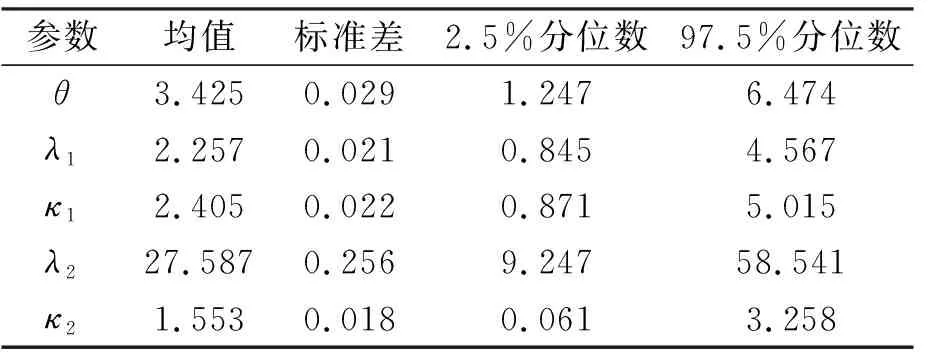
表6 模型参数贝叶斯更新参数后验分布统计值

4 地铁运营安全可靠性分析

以上详细的介绍了基于Copula函数和参数贝叶斯更新的净空收敛(CD)和差异沉降(DS)二元离散时变相依模型构建过程，为验证该模型的准确性和实用性，将该模型运用于武汉地铁长港路—汉口火车站堆载区间的安全可靠性评价上，拟用该模型精确评估盾构地铁区间的安全状态，并用该结果指导运营地铁的安全管控。

4.1 基于可靠度理论的运营安全控制

确定盾构地铁结构的风险状态水平，有助于对运营盾构地铁结构的安全进行管控。本文将系统的失效概率作为判断建筑风险状态的基础，为研究盾构地铁结构的安全可靠性，采用蒙特卡洛模拟法确定系统的失效概率，计算公式为：

(15)

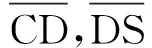
国内外的“可靠度设计统一标准”[13, 14]，均给出与结构安全等级对应的最小目标可靠性指标。在结构完成设计后，结构的最小目标可靠性指标往往被用于结构的安全性校核，若设计出的结构可靠性指标大于与设计安全等级对应的最小目标可靠性指标，便可认为该结构满足安全性要求。本文提出承载能力极限状态下结构的可靠性指标值，如表7所示。

表7 可靠度指标β的地铁隧道安全分级标准

本文综合分析了以上各个规范的规定，提出了根据结构安全可靠度指标β的地铁隧道安全等级划分标准(见表7)。其运用思路如下：首先得出基于正常使用极限状态下结构的失效概率，其次得出地铁隧道安全可靠度指标β，再次利用表7得到此时地铁隧道所处的安全等级，最后得出地铁运营时所需保护措施。

4.2 盾构地铁运营安全可靠度对比分析

受到周围多源不确定性环境因素的影响，地铁结构通常存在一定的变形响应，而一些变形指标经常被作为关键性能指标(Key Performance Indicators，KPIs)用于评判盾构地铁结构的安全服役状态，采用净空收敛和差异沉降作为盾构地铁运营安全可靠性分析的评价指标。

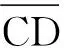
利用2016年4月1日的监测数据，若不考虑参数的相依性构建100000组数据的净空收敛(CD)和差异沉降(DS)散点图如图6所示，可见参数独立时CD和DS的分布非常离散，均匀的分布在坐标系内。同时，利用Copula理论构建了CD和DS的二元联合分布模型，利用蒙特卡洛法能够得到100000组数据点，用于盾构地铁运营安全的可靠性分析，如图7所示。从图6，7可知，利用Copula函数构建的相依性模型生成的散点较独立时更加集中，且不同Copula相依模型有不同的聚集特征，表征了不同的参数相依特性。

图6 参数独立时左右线CD和DS散点图

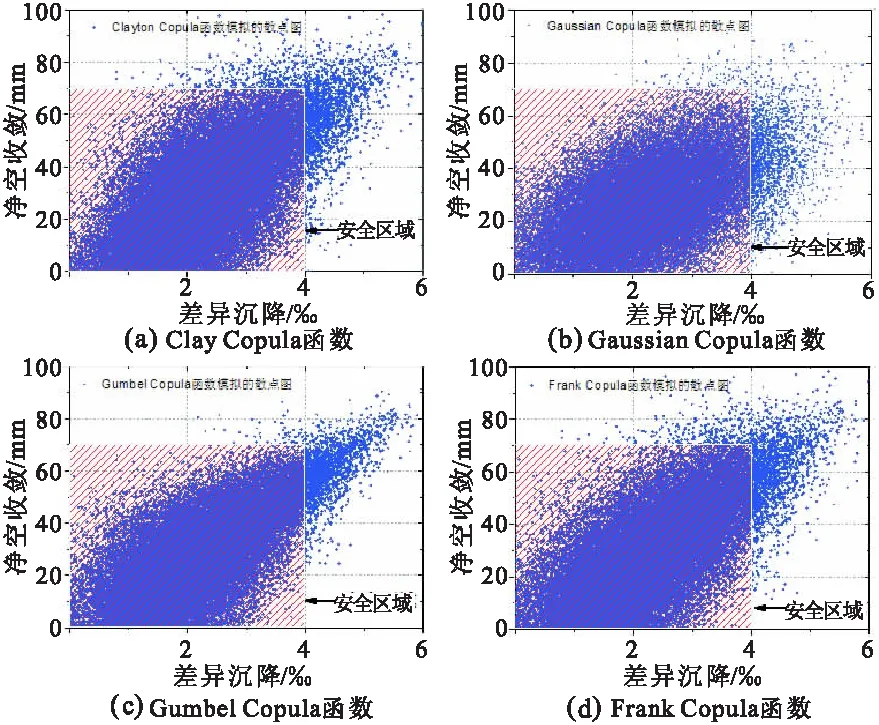
图7 左线不同Copula函数模拟CD和DS散点图

为比较直观地观察系统的失效区域，图6， 7给出了系统安全区域示意图，处在该区域外的散点为失效点。根据蒙特卡洛法基本原理，系统的失效概率值为处于安全区域外散点占全部散点的比例值。对比图6，7发现，Copula相依性模型改变了散点的分布规律，从而影响了系统的失效概率和可靠度。事实上，现实的参数之间存在一定的相依关系，意味着传统的参数独立模型计算可靠度结果的不准确性，表明了利用所采用的相依性模型能够提高系统可靠性计算的精度。

在2016年4月1日监测数据的基础上，利用可靠度理论可以利用各Copula函数构建的相依性模型，得出系统的pf如表8所示。由表8可知，不同的Copula函数计算得到的pf不同，以盾构地铁左线为例，pf最大的是Gaussian Copula为0.02688，其次是Gumbel和Frank Copula为0.02484，0.02466，Clayton Copula的失效概率值最小为0.02180，最大值(Gaussian Copula)和最小值(Clayton Copula)之间相差23.3%，表明不同的Copula函数相依模型的计算结果可能相差较大。由于经AIC和BIC准则判断出最优Copula函数是Frank Copula函数，故而选取Frank Copula函数的计算结果为最终得到的失效概率结果。对比Frank Copula相依性模型和相互独立时计算得出的pf发现，两者差值为0.01126，相差45.6%，表明利用相依性建模的结果与参数独立的情况相差非常大，进一步验证了利用相依性建模的准确性和必要性。

表8 不同Copula模型及相互独立下地铁结构的pf %

利用失效概率pf可以得到系统的可靠度指标β见表9，从表9可知，该区段左右线盾构地铁的β值皆小于2.3，2016年4月1日，该区段的地铁左右线区间均处于IV级风险，需制定运营风险控制专项研究方案，严密监测地铁运营的安全状态。

表9 不同的Copula模型及相互独立下地铁结构的β

4.3 基于贝叶斯-Copula模型的可靠度

2016年4月14日下午—2016年4月20日进行地面卸土，同时中铁隧道院进行隧道内监测，武汉路源工程质量检测有限公司进行裂缝检测。于4月14日起，开始采用加固措施：(1)借鉴武汉地铁4号线一期洪—汉区间隧道内裂缝处理的实际经验，针对收敛小于7 cm且裂缝宽度大于0.2 mm的管片，对于隧道顶开裂的管片分块，首先采用环氧浆液压力注浆封闭裂纹，然后采用粘贴芳纶布处理；(2)借鉴武汉地铁盾构施工期间受损管片加固补强措施，对于收敛大于等于7 cm且裂缝宽度大于0.2 mm的管片，首先采用环氧浆液压力注浆封闭裂纹，然后在隧道内内衬钢圈进行加固处理。

在2016年4月1日—2016年4月30日监测数据的基础上，利用各Copula函数构建二元离散时变相依模型，分别得出的左右线盾构地铁结构的可靠度指标β值，如图8所示。从图8可以明显地观察到采用不同相依模型的区别，参数独立时的β计算值明显小于采用Copula函数构建的模型，各模型计算的可靠度指标之间的差异值比较稳定，表明本文构建的相依模型的稳健性。

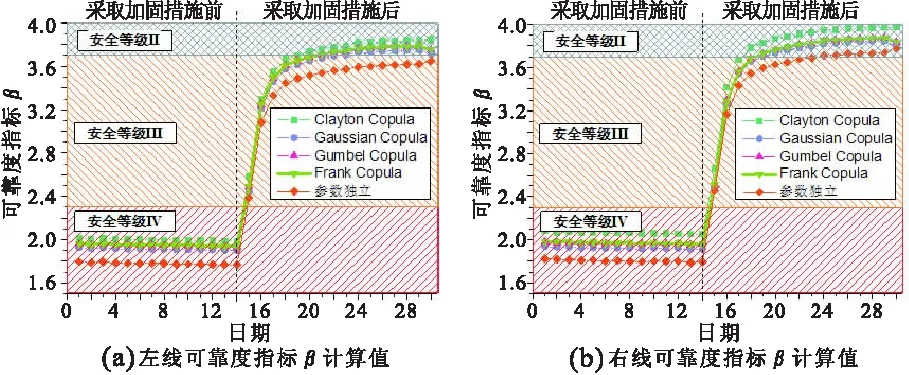
图8 盾构地铁左右线可靠度指标β计算值

由图8可知，在采用加固措施前，地铁的安全等级为IV，采取措施后地铁的可靠度指标值急剧增加，以Frank Copula的计算值为判断依据发现，左右线地铁分别于4月21日和4月19日达到安全等级II，表明了加固措施的有效性。该结论也说明了利用本文构建的二元离散时变相依模型，能够较为敏感地捕捉到盾构地铁结构安全性的变化规律，验证了该模型的精确性和实用性。

5 结 论

Copula相依性建模理论能够准确描述参数之间的相关性的特点，并结合贝叶斯更新技术能够体现时变效应对模型的影响特征，基于此提出了基于Copula函数和参数贝叶斯更新的净空收敛(CD)和差异沉降(DS)二元离散时变相依模型构建过程，以武汉地铁2号线某段区间为工程背景，验证了该模型的准确性和实用性，得到以下结论：

(1)基于左右线净空收敛和差异沉降原始监测数据，利用四种不同的Copula函数构建净空收敛值和差异沉降值的联合分布函数，并识别出差异沉降(DS)和净空收敛(CD)的最优边缘分布类型是Weibull分布，两参数的最优Copula函数是Frank Copula函数。

(2)对比Frank Copula相依性模型和相互独立时计算得出的失效概率pf发现，两者差值为0.01126，相差45.6%，表明利用相依性建模的结果与参数独立的情况相差非常大，进一步验证了利用相依性建模的准确性和必要性。

(3)详细介绍了基于Copula函数和参数贝叶斯更新的净空收敛(CD)和差异沉降(DS)二元离散时变相依模型构建过程，并进一步研究使用该模型进行地铁运营安全的可靠性分析。得到采用不同相依模型的区别，参数独立时的β计算值明显小于采用Copula函数构建的模型，各模型计算的可靠度指标之间的差异值比较稳定，表明了构建的相依模型的稳健性。而且能够较为敏感地捕捉到盾构地铁结构安全性的变化规律，验证了该模型的精确性和实用性。